一道2023年奥林匹克竞赛试题的多解及推广
文帅 徐凤旺 梁明端

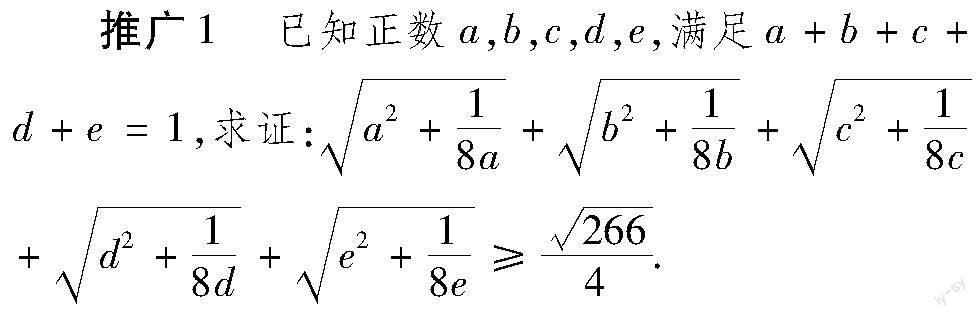
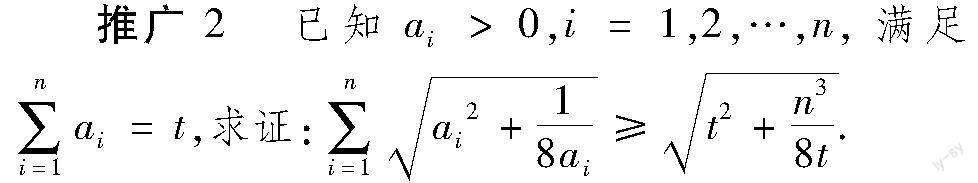
1.试题呈现
分析:这是2023年全国中学生数学奥林匹克竞赛东莞市预赛试题的一道求最值问题,其中已知条件与所求式子结构对称,M的表达式是由4个根式的和组成,每一个根式的被开方数均为整式与分式的和,形式上具有数学的美感,本文对该题进行多解探究,并对其进行变式和推广.
2.解法探究
+1-d=4-(a+b+c+d)=3,故M的最小值为3.
评注:此解法利用基本不等式与配凑法将每一个根式进行放缩,从而利用已知条件求得M的最小值.
评注:此解法两次利用基本不等式的推广将根式下的被开方数进行放缩,从而求得M的最小值.
評注:此解法利用切线的性质,将问题转化为求函数最值问题,从而求得M的最小值.
评注:此解法利用函数的凹凸性与琴生不等式,将问题转化为求函数最值问题,从而求得M的最小值.
评注:此解法利用柯西不等式将每一个根式进行放缩,再用基本不等式的推广求得M的最小值.
评注:此解法利用赫尔德不等式与闵可夫斯基不等式,求得M的最小值.
3.试题推广
分析:此推广是将试题中的未知数个数从“4”元推广到“5”元,推广的形式不变.
分析:推广2是在推广1的基础上,将不等式未知数个数从“5”元推广到“n”元,条件式子的结果从“1”推广到“t”,推广的形式不变.
分析:推广3是在推广2的基础上,将推广2中不等式每一个根号下的系数“1”和“8”推广到“λ”和“μ”,推广的形式不变.
分析:推广4是将试题条件中的条件式子结果从“1”推广到“t”,以及改变代数式的未知数的幂及结构得到的.
分析:上述推广1到推广4均是推广5的特例,下面列举推广5的证明过程,其他推广的证明过程不再叙述.
推广,对于数学学习与数学研究有着十分重要的意义.在数学学习中,推广可以加强观察、分析、比较、综合、概括、归纳、类比和发现的能力,拓展不同的解题思路,提升创造性的思维.在数学研究中,推广可以产生新问题与新方法,加深自身对问题的认识与理解.在数学竞赛中,推广可以激发学习兴趣与求知欲,引领新的发现[1].
参考文献
[1]朱华伟,张景中.论推广[J].数学通报,2005(04):55-57+28.

