经典文化背景下的试题赏析与教学实践
谢盛富


1 引言
《课程标准》明确指出,“数学承载着思想和文化,是人类文明的重要组成部分.”“在教学活动中,教师应有意识地结合相应的教学内容,将数学文化渗透在日常教学中,引导学生了解数学的发展历程,认识数学在科学技术、社会发展中的作用,感悟数学的价值,提升学生的科学精神、应用意识和人文素养;将数学文化融入教学,还有利于激发学生的数学学习兴趣,有利于进一步理解数学,有利于开拓学生视野、提升数学学科核心素养.”数学文化是经典文化的重要组成部分,是高考题、各地模拟题的命题方向之一.纵观近年数学题,常以传统的数学文化(尤其是数学名著)为背景进行命题,特别是结合经典的、各学科的、各领域等有关文化成就或现代科技发展等命制新颖试题,从中引导学生感悟数学独特的学科价值、多维的文化价值、广泛的应用价值、丰富的审美价值和德育价值,这正是数学教育塑造学生德智体美劳全面发展的正确价值观的一种有效途径.
2 试题赏析
例1 (2023年北京卷·9)坡屋顶是我国传统建筑造型之一,蕴含着丰富的数学元素.安装灯带可以勾勒出建筑轮廓,展现造型之美.如图1,某坡屋顶可视为一个五面体,其中两个面是全等的等腰梯形,两个面是全等的等腰三角形.若AB=25 m,BC=AD=10 m,且等腰梯形所在的平面、等腰三
A.102 m B.112 m C.117m D.125 m
分析:本题以建筑造型之一的坡屋顶为试题命制背景,展示数学问题源于生活、贴近学生的实际、数学与生活息息相关,展现我国古代劳动人民的智慧与创造,考查学生的阅读理解能力,考查立体几何的结构特征,考查数学建模、数学运算、数据分析,考查学生灵活应用数学知识分析问题、解决问题的能力.
实际上,在近年高考试题中,也涌现了不少以建筑有关为背景的试题,比如,2022年全国卷Ⅱ第3题以“古代建筑中的举架结构”与“古代建筑屋顶截面”为背景,考查等差数列和斜率的计算;2022年天津卷第8题以“十字歇山”为背景,考查几何体的体积计算;2020年全国卷Ⅰ第3题以“埃及胡夫金字塔”为背景,考查高与边长的比值计算;2020年全国卷Ⅱ理科第4题以“天坛的圜丘坛”为背景,考查等比数列的求和;2018年全国卷Ⅲ第3题以“榫卯”为背景,考查三视图的判断.
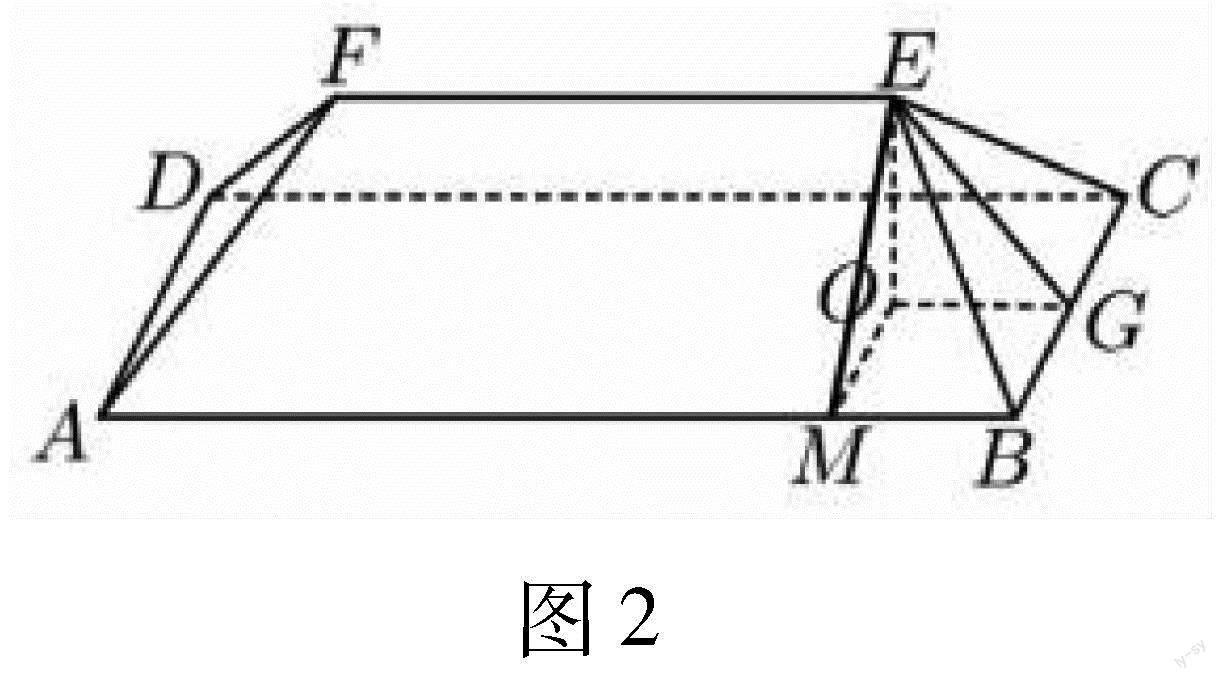
详解:如图2,过点E作EO⊥平面ABCD,垂足为O,过E分别做EG⊥BC,EM⊥AB,垂足分别为G,M,
变式 在例1条件不变的情况下,教学中可以改变提问方式,以便更好地系统复习立体几何的面积与体积公式并利用空间向量计算空间角等问题.比如,(1)求该五面体的体积(或某个面的面积);(2)求直线AF与直线CE所成的角;(3)求直线BE与平面ABCD所成的角,等等.
3 教学途径
教学实践中,可根据不同内容或不同年龄段,采取不同的教与学方式,丰富学生的多样化学习方式,或改进学习方法,如收集资料、实践探索、调查研究、合作交流、自主探究、小论文写作等,感受不同时期经典文化及其呈现方式,让学生通过多种途径接受经典文化的浸润及熏陶,发挥情感教育的目标功能,立足高考而不囿于高考.其主要途径有:
(1)植入传统的数学文化
以往的课堂、试题在数学文化层面下了很大功夫,比如借助名人诗词或文章、古代数学成就、数学名著等进行命制试题,融合数学知识、思想方法及能力,创新试题情境,设置合理的数学问题,考查数学知识、能力,有效考查学生的创新意识和应用意识,培养学生的探究精神,渗透数学核心素养.
(2)利用教材阅读材料、图书馆或网络
以阅读材料为基础,通过图书馆或网络搜集、查找、阅读有关文献资料,调动学生积极参与,理解数学、感悟数学,弘扬美德、陶冶情操,体验经典文化育人的过程,激发热爱学习情感,树立宏伟志向,对青少年树立正确的世界观、人生观和价值观有很大的帮助.
以教材人教A版第二册为例,第6页阅读与思考“向量及向量符合的由来”,让学生了解向量的起源、发展及应用,明了向量在各学科各领域中都有广泛的应用,成为解决各种问题的有力工具;第55页阅读与思考“海伦与秦九韶”,让学生了解古人是如何计算三角形的面积,知晓秦九韶的“三斜求积”比海伦公式早发现约600年,感受数学家对数学发展产生的广泛影响;此外,复数、立体几何、统计、概率章节也有相关的阅读材料,极大丰富了教师的教学内容和学生学习的素材.
(3)民风民俗与现代时尚相融合
社会在发展,民风民俗也在不断传承与创新,实现创造性转化、创新性发展. 民俗文化是在古中国的土壤与气候中孕育绽放的,生肖、节气、太极、八卦、阴阳、五行、清明、端午、中秋、春节、年画、舞狮、武术、蹴鞠、剪纸、课本剧、歌谣、灯谜、谚语等均具有历史性的传承与发展,或创新,在各地集年货、美食、民俗等于一体的新春庙会就是经典文化与现代时尚深度融合的一种方式. 以她们为问题背景,可增强社会责任感,同时渗透数学的应用;或融入到试题情境中,树立家国意识,增强爱国情怀.
例2 猜灯迷是我国一种民俗娱乐活动,某社区在元宵节当天举办猜灯谜活动,工作人员给每位答题人提供了5道灯迷题目,答题人从中随机抽取2道灯迷题目作答,若2道灯谜题目全答对,答题人便可获得奖品.若甲只能答对工作人员所提供的5道题中的2道,则甲能获得奖品的概率为.
(4)巧借学科外延渗透在试题中
《课程标准》明確指出,“D类课程包括美与数学、音乐中的数学、美术中的数学、体育运动中的数学”;“E类课程包括拓展视野、日常生活、地方特色的数学课程”,因此数学科外延是多姿多彩、多元广泛化的,给一线教师和学生无限的展示空间,展现数学在人文学科中的应用,感受数学的美学价值.
例3 中国四大名亭中,醉翁亭位于安徽省州市西南琅琢山麓,爱晚亭位于湖南省长沙市岳麓山清风峡中,湖心亭位于浙江省杭州市西湖中央,陶然亭位于北京市南二环陶然桥西北侧;江西南昌的滕王阁、湖南岳阳的岳阳楼和湖北武汉的黄鹤楼,被誉为“江南三大名楼”.小李同学要从这四大名亭、三大名楼中随机选取2个去旅游,则爱晚亭、岳阳楼中至少有一个入选的方案有种.
4 教例实践
例4 (多选题)古希腊著名的毕达哥拉斯学派把1,3,6,10,…这样的数称为“三角形数”,把1,4,9,16,…这样的数称为“正方形数”.如图3中可以发现,任何一个大于1的“正方形数”都可以看作两个相邻“三角形数”之和,下列等式中,符合这一规律的表达图3式为( ).
A.25=9+16B.36=15+21C.49=18+31D.64=28+36
(展示试题在多媒体上,然后先简单介绍毕达哥拉斯学派的有关学说、成果.)
教师:毕达哥拉斯学派,创立于公元前6世纪末,古希腊的重要学派之一,学派成员由数学家、音乐家、天文学家、科学家等组成,普遍采用辩证法思想,对当时和后世都产生了深远影响. 学派的基本思想是“数是万物的本原”,认为世间万物都是由一定的数量关系构成的,数量的比例决定了这个世界的某些事物是否和谐.美表现于数量比例上的對称与和谐,和谐起于差异的对立,美的本质在于和谐. 他们很注意研究数,对整数进行了深入研究,尤其注意形与数的关系,还依据几何和哲学的神秘性来对“数”进行分类,按照几何图形分类,可分成三角形数、正方形数、长方形数、五角形数等.对整数进行分类,如整数中包含有奇数、偶数、质数、亲和数及完全数等,还提出了一些悖论.我们所熟悉的勾股定理也是毕达哥拉斯发明的,毕达哥拉斯为了庆贺自己的业绩,杀了一百头牛,因此勾股定理亦称百牛定理.
教师:本题中“三角形数”与“正方形数”在往年高考试题中出现过,比如2009年湖北卷第10题、2012年湖北卷文科第17题、2013年湖北卷理科第14题等,均是以“三角形数”与“正方形数”为载体考查数列、逻辑推理等.回到本例,应如何求解呢?
学生1:观察图形的规律,对后续图形逐个画出来,仿照题干中的方法进行分解,可得到正确答案.
追问1:这个方法虽然麻烦,却也很直接!有没有其它解法?站在数列的角度尝试思考,三角形数和正方形数有什么规律?
追问2:很好.接下来,我们如何探寻正方形数与三角形数之间的关系,即“正方形数”是两相邻“三角形数”的和.
学生3:三角形数从1开始,第几个三角形数就是从1开始的连续自然数相加到几,正方形数也就是2的平方就是第1个三角形数加第2个三角形数,3的平方就是第2个三角形数加第3个三角形数,4的平方就是第3个三角形数加第4个三角形数,5的平方就是第4个三角形数加第5个三角形数,6的平方就是第5个三角形数加第6个三角形数,7的平方就是第6个三角形数加第 7个三角形数.因此可知正确选项为BD.
追问3:很好.还有其它想法吗?
学生4:由已知条件得到三角形数依次为1,3,6,10,15,21,28,36,45,…,由于正方形数是这组数据中的相邻两数之和,容易得到:25=10+15,36=15+21,49=21+28,64=28+36,只有BD是正确的.
教师:太漂亮了.同学们通过阅读、审题,能够借助图形善于观察特征,通过探究数与数之间的关系发现规律,从试题情境中得到正确的答案,为你们点赞.
设计意图:从最基本的问题情境,渗透经典文化,了解文化背景,关注学生的认知规律,引导学生尝试求解,激发学生可贵的探究兴趣,再多次追问、挖掘题干中信息,在碰撞中启发学生的发散思维,从感性认识上升到理性思维,回归数学本真,用数学的眼光看待世界.
5 结语
数学文化下的试题命制从数学名著、数学家的成果、猜想等命题背景逐步向经典文化转变,不断创新,不断设置新情境,为数学问题的命置提供了一种新方向.这能更多地在学科外延、数学思想、数学之美、贴近生活的案例渗入教材、融入课堂,植入在数学试题中,让数学教学变得生动有趣,由此达到,培养学生的探究精神与应用意识,提升知识与能力的应用水平,合理培养学生的创新精神,提升思维品质与解题能力,培养学科核心素养,不断丰富和完善经典文化在数学教育中的价值.

