北票市农村饮水工程管道水质安全评价

艾宏伟

(北票市水务综合行政执法队,辽宁 北票 122100)

随着农村经济的不断发展,村民对生活用水质量的要求越来越高[1]。饮用水质安全直接关系着村民身心健康,这也是村民生存发展的基本要求。在向用户输配生活用水过程中农村饮水工程输配水网发挥着重要作用,由于生物、化学和物理作用使得输配水质存在一定波动。所以,用户水质优化的核心就是实现输配水管道水质安全的科学评价[2-3]。对于复杂输配水管网系统中的所有节点和管道实施人工检测,难以准确反映水质变化情况且实现难度较大。因此,文章充分考虑农饮水工程特点提出复合粒子群法,对及时掌握管道水质变化情况以及保证供水水质安全极具现实意义。

1 研究方法

1.1 水质数据分类方法

1)粒子群算法设计。粒子群算法与同类进化法具有一定相似性,主要通过“进化”和“群体”过程实现鸟类群体行为的模拟。该算法以微粒个体的适应度作为计算核心,待优化问题的解利用离子方位来确定。一般地,在粒子群算法中每个粒子的适应度与其性能的状况密切相关。通过设置粒子速度,可以确定每个粒子的飞行速率和方位,从而逐步接近最优解。例如,在处理水质数据时,可以将每个水质粒子的方位表示为Yj(h)=[yj1(h),yj2(h),…,yjn(h)],并将粒子的飞行速度表示为Uj(h)=[uj1(h),uj2(h),…,ujn(h)]。在开始计算之前,需要初始化处理水质粒子的速度和方位,并通过跟踪极值的方式来刷新其速度与方位,通过多次迭代运算逐步确定最优解。

具体来说,个体极值Qj(h)=[qj1(h),qj2(h),…,qjn(h)]可以选用粒子自身检索的最优解,全局极值Qf(h)=[qf1(h),qf2(h),…,qfe(h)]可以使用截至当前达到的粒子群最优解,其中qjn(h)和qfe(h)为表示当前和所有粒子水质数据。在e维计算时,可以按照公式(1)～(2)不断更新每个粒子j的速度和方位,以使其靠近个体极值和全局极值,即:

uij(h+1)=ω·uij(h)+d1rand2i(h)[qjn(h)-yjn(h)]+d2rand2i(h)[qjn(h)-yin(h)]

(1)

(2)

式中:i、j为数量;ω、d为惯性权重系数和加速系数;rand、sig为随机数和Sigmoid函数。通过公式(1)、(2)可以反映粒子之前的惯性与速度及其“认知”行为,这体现了粒子之间的相互协作和信息共享关系。

2)数据编码。该过程就是将离散化的混合数据,通过粒子首层、第二层结构进行分类处理,即通过两层相融来完成编码分类,任一可行解与与水质粒子的一种编码相对应。数据属性连续分割点的编码为首层,以二进制编码设置所有非间断属性分割点,分割点数目总值即为码长度总值,某一水质粒子是1或0时则代表使用和不使用该分割点,即水质粒子后续层间编码工作可继续或终止,例如,对于b1、b2选择分割点的问题,使用1010010来表示首层编码,在第二层中可以将粒子结构分为分类、离散和连续编码,实现混合水质数据编码。

3)分类流程。步骤1:在水质数据分类过程中,需要定义适应度函数来评估每个水质粒子的分类效果,同时还需要设定合适的惩罚系数和迭代次数,在初始化阶段将复合粒子群Y(h)的速度和方位设定为初始值。步骤2:根据设定的适应度函数,对每个水质粒子在Y(h)中的分类效果进行评估,如果某个水质粒子的分类结果都为0(即无有效分类),则将其适应度值设置为很小的值。步骤3:将每个水质粒子的当前最佳分类方案(qbest)与其对应的适应度值进行比较,如果某个水质粒子的适应度较高,则其分类效果较好,将其设定为当前阶段的最优方案。步骤4:将全局最优方位Qf(h)作为参考,对比分析各个水质微粒的适应度值,如果某个水质微粒的适应度值较高,重新设定其索引号。步骤5:确定各个粒子的方位和速度,根据水质微粒的非间断离散化属性和分类结果,确定每个粒子的方位和速度。这些属性和结果将直接影响粒子的适应度大小。步骤6:判定是否达到最大迭代次数,如果已经达到了预设的最大迭代次数则直接进入步骤8,结束分类过程,否则返回步骤3继续迭代。步骤7:根据设定的终止条件,判断是否继续进行迭代,如果未达到终止条件返回步骤2,继续计算适应度和更新粒子的方位与速度。步骤8:根据最优粒子的分类方案,对水质数据进行分类处理,准确地反映水质数据的个别与整体属性,从而减少后续的运算量。

1.2 评价分析

考虑指标权重将分类后的水质数据作为分析单元计算各指标的单因子水质标识指数,每个指标权重利用超标法确定,然后通过加权求和获取能够全面反映输配水管道水质的综合水质标识指数,科学评定管道水质级别[4]。

1)计算单因子标识指数。根据水环境质量标准利用公式(4)计算氨氮、生化需氧量BOD和化学需氧量COD的单因子标识指数,对于递减类指标溶解氧DO可以利用公式(5)计算其单因子标识指数[5-6],即:

(3)

(4)

式中:Hj、Dj为指标j的水质类别和实测浓度值;Rjh上、Rjh下为在第Hj类水区间内指标j的上、下限值。若氨氮、BOD和COD存在6个分类标准,所其对应的水质标识指数为:

(5)

2)指标权重计算。针对各指标权重利用超标赋权法确定,该方法既可以保证权重的合理性,还能够重点突出超标因子的作用。采用超标倍数法确定各指标权重,如遇氨氮、BOD和COD的超标倍数可利用下式计算[7-9]:

(6)

式中:Rj5为水质的五级标准。溶解氧DO达到一级时取0,否则利用下式确定:

(7)

式中:R5DO、R1DO为溶解氧DO的五级和一级标准,其中R1DO的计算公式为:

(8)

式中:W为水温。通过归一化处理各超标倍数值可以确定氨氮、BOD和COD指标权重,即:

(9)

3)综合表示指数计算。采用加权求合法处理单因子标识指数即可确定综合标识指数,其表达式为:

(10)

根据计算的综合标识指数可以评定输配水管道水质安全级别,其中一、二、三、四、五、六级水质所对应的综合标识指数Q取值区间为1.1～2.0、2.1～3.0、3.1～4.0、4.1～5.0、5.1～6.0和>6.0。

2 实例应用

采用复合粒子群方法定量评价北票市2020年农村饮水安全巩固提升工程管道水质安全等级[10-12],如表2所示。

表2 输配水管道水质安全等级

为了评价复合粒子群方法的可靠度,对比分析输配水管道水质检测实际值与该方法评价结果,如表3所示。

表3 复合粒子群方法与实际值是否相符

从表3可以看出,输配水管道水质实际情况与复合粒子群方法基本一致,该方法具有较高可靠度,对定量评价农村饮水安全巩固提升工程管道水质具有较强适用性。

采用层次分析法和模糊数学法定量评价北票市2020年农村饮水安全巩固提升工程管道水质安全,计算不同方法评价时延和结果均方误差如表4所示。

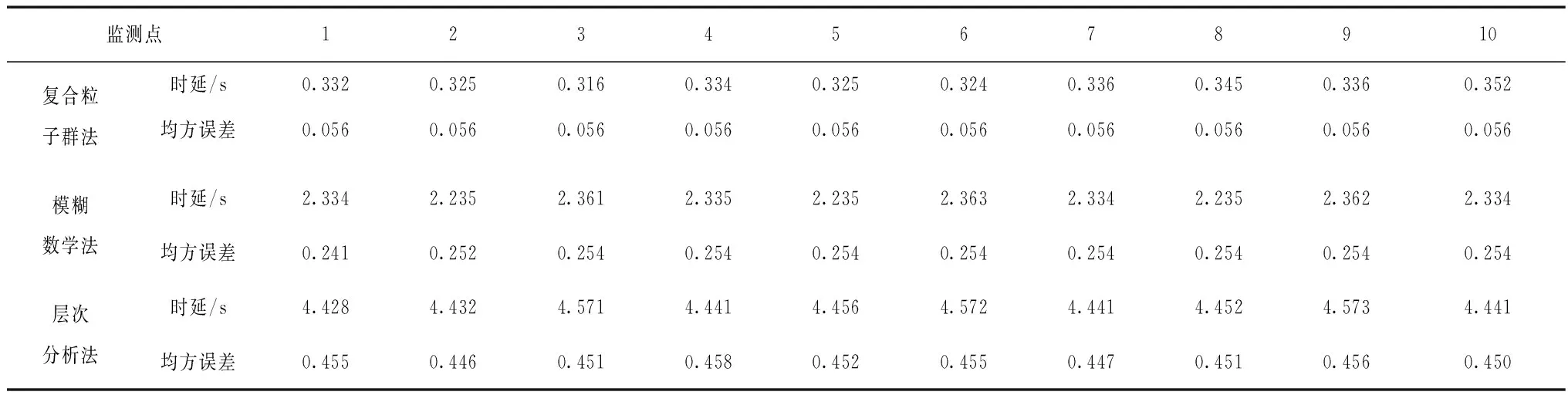
表4 基于不同方法的性能测试结果

由4可知,复合粒子群法相比于层次分析法和模糊数学法的均方误差总体较小,其最大值只有0.056;从延时的角度上,复合粒子群法相比于层次分析法和模糊数学法具有更快的运算效率。

对北票市2020年农村饮水安全巩固提升工程管道水质安全应用复合粒子群法、层次分析法和模糊数学法进行定量评价时,对溶解氧DO、氨氮、生化需氧量BOD和化学需氧量COD的查全率及查准率如图1所示。

图1 查全率与查准率

从图1可以看出,采用复合粒子群法定量评价输配水管道水质时,对溶解氧DO、氨氮、生化需氧量BOD、化学需氧量COD的查全率和查准率分别为0.97及0.98,该方法整体高于层次分析法和模糊数学法的查全率及查准率。

3 结 论

1)为定量评价输配水管道水质级别研究提出一种复合粒子群方法,该方法相比于层次分析法和模糊数学法的均方误差总体较小,其最大值只有0.056,从延时的角度上该方法具有更快的运算效率。

2)采用复合粒子群方法定量评价管道水质安全级别时,对溶解氧DO、氨氮、生化需氧量BOD、化学需氧量COD的查全率和查准率分别为0.97及0.98,该方法整体高于层次分析法和模糊数学法的查全率及查准率。