基于智能优化算法的PCB板电子元件条件热布局优化及仿真分析

舒 红

(陕西工业职业技术学院,陕西 咸阳 712000)

PCB板(Printed Circuit Board)是电子元件的重要组成部分,在现代电子工业中起着至关重要的作用[1]。随着电子产品的不断发展及复杂化,PCB板上的电子元件数量和布局越来越复杂,需满足热管理需求。引入智能优化算法,通过蚁群算法实现PCB板上电子元件的条件热布局优化,提高电子产品的稳定性及工作效率,为PCB板设计提供一种新的优化方法和思路。

PCB板承载着各种电子元件并提供电气连接,电子元件的热布局对于整个电路板的热性能及稳定性起着至关重要的作用[2]。合理的电子元件热布局可有效降低电子元件之间的热交互,提高散热效果,保证电路板的稳定性及可靠性。在PCB板的电子元件热布局中需考虑很多因素,包括元件的功耗、散热条件、布线结构等。近年来,智能优化算法在这一领域展现出了强大的优势,遗传算法、粒子群算法、蚁群算法等智能优化算法被广泛应用于此问题中,可以有效提高PCB板的散热效果,降低元件之间的热交互,保证整个电路板的稳定性和可靠性。

1 蚁群算法模型

蚁群算法的整个计算过程可概括为两个方面,即适应阶段和写作阶段[3-4]。其流程是给定一个有n个城市的集合体{1,2,3,…,n},每个蚂蚁从原点出发走遍集合体中的每一座城市,且每座城市只走一次,最终回到原点,其最终目的是找到每一只蚂蚁走过的所有路径之和为最小的情况。相关参数定义如下:蚂蚁的总数量记为m;i、j两个城市之间的路径距离记为dij,(i,j=1,2,3,…,n);在时刻t时,蚂蚁在i、j两个城市之间的信息素轨迹量记为πij(t),蚂蚁在原点时,设定每条路径上的信息素为一个常数值,记为πij(t)=c,即此时每条路径上的信息素轨迹量是相等的。等蚂蚁k(k=1,2,3,…,m)选择城市i出发到城市j时,影响其选择的有两个因素:两个城市之间的可见度ηij,从城市i出发到城市j的可行性,其由迄今为止城市之间路径上的信息素浓度πij决定。采用蚁群算法能够实现最优解,主要遵循以下几个准则:

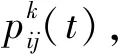
式中:allowedk=[0,1,2,…,n-1]-tabuk,tabuk表示蚂蚁k下一步能够选择的城市。α为蚂蚁残留下来的信息素的相对重要程度,即α值越大,蚂蚁越重视这条路径,选择这条路径的概率也越大,但α值如果出现过大情况会导致蚂蚁提前搜索而收敛。β为期望值的相对重要程度,主要是指启发信息量的受重视程度。ηij表示蚂蚁从城市i出发到城市j的期望值,由启发式函数确定,如ηij=1/dij。在算法计算过程中设定的蚂蚁数量越多,相应的算法全局搜索能力越强。但如果蚂蚁的数量过多,算法在计算过程中会导致收敛速度变慢。因此,通常选用的蚂蚁数与城市数目相同。

2)局部调整优化准则。蚂蚁个体在寻求最优解的过程中需要逐步对信息素进行调整,从而更快地找到最优解。当蚂蚁经过多次循环经历时间为h时,被选择的两个元素之间的信息素调整规则为:

πij(t+h)=(1-ζ)·τij(t)+ζτ0,τ0=1/(nlmin) 式中:τ0为局部更新常数,ζ⊂[0,1]表现信息素的气味蒸发因子,lmin表示集合中最近两个元素之间的间距。

3)全局调整优化准则。每只蚂蚁在进行一次完整的寻优过程后,需对其进行一次完整的全局调整,调整规则为:

τij(t+1)=(1-ρ)·τij(t)+ρΔτij

为了避免蚁群算法应用过程中出现早熟停滞现象,引入最大最小蚂蚁系统进行算法改进,改进流程如下:

更新信息素。在最大最小蚂蚁系统进行迭代后,当系统找到最短路径的那只蚂蚁才选择更新其信息素,更新原则为:

τij(t+1)=(1-ρ)τij(t)+Δtbestij

式中:Δtbestij=1/f(Tbest),f(sbest)表示迭代或全局迭代得到的最优解(Tgb)。一般来说,蚁群系统主流采用全局最优解sgb,最大最小蚂蚁系统主要采用的是迭代最优解sib,用以扩大算法搜索范围,避免过早发生早熟停滞。

限制信息素。在蚁群算法分析过程中,任意两个城市之间的信息素远远大于其他路径选择时,根据概率选择原则,蚂蚁更倾向于选择信息素多的路径,算法具有正反馈机制又会进一步增强该条路上的信息素浓度,会进一步引导所有蚂蚁趋向于选择这条路径,停滞搜索。为避免这种现象,最大最小蚂蚁系统对于信息素的值限制在[τmin,τmax]中,使所有信息素满足τmin≤τij(t)≤τmax,避免不同路径之间的信息素浓度差距过大。

为了使算法在初始迭代中增大其搜索范围,能够进一步寻优,通常将各路径的信息素轨迹量初始化为τmax,增强蚁群算法的随机搜索能力。

图1为蚁群算法寻优最优解Tgb算法的流程和代码过程。

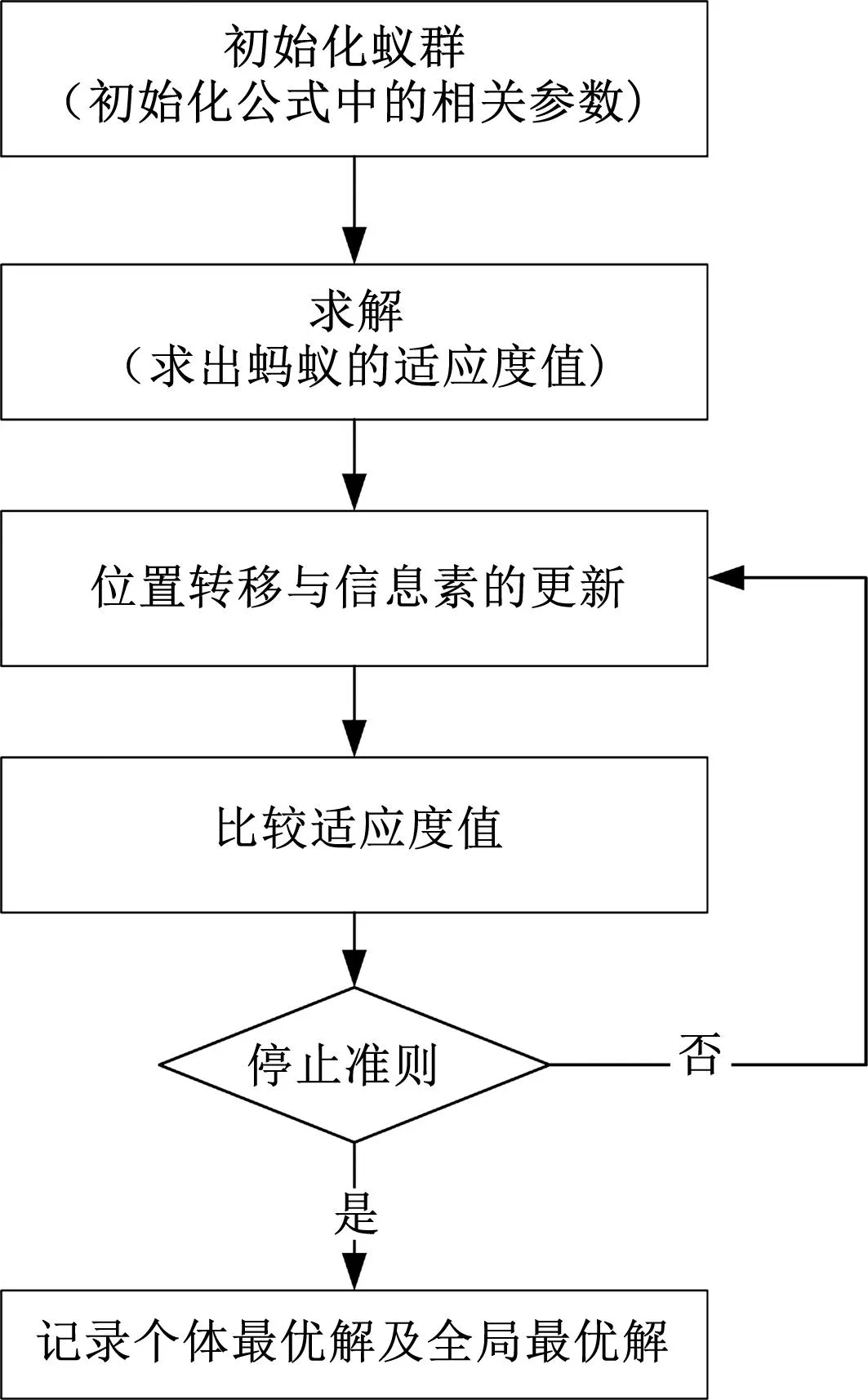
图1 蚁群算法寻优流程Fig.1 Ant colony algorithm optimization process from ant_colony import AntColony import numpy as np

# 构建距离矩阵

distance=np.array{[(0,29,20,21),(29,0,15,24),(20,15,0,26),(21,24,26,0)]}

# 创建蚂蚁群实例

colony=AntColony(distance,4,10,100,0.95,alpha=1,beta=2)

# 运行蚁群算法

shortest_path=colony.run()

print(″最优路径:″,shortest_path)

2 优化过程与结果

2.1 优化的PCB板电子元件条件热布局

对优化结果进行计算对比计算。设定蚁群算法中蚂蚁的数量为10,公式中的相关参数初始化值为α=0.5、β=5,设定迭代次数为1000[5]。在matlab环境下运行算法流程,结果如图2所示,优化的PCB板电子元件条件热布局的温度值结果如图3所示。

图2 优化的PCB板电子元件布局Fig.2 Optimized PCB board electronic component layout

图3 优化的PCB板电子元件条件热布局的温度值Fig.3 Optimized temperature values for the conditional thermal layout of PCB electronic components(℃)

图2中数值的大小代表序列中功耗s1,s2,s3,…,sn的排序,通过蚁群算法优化后可得到系统最优分布状况。

图3表示采用蚁群算法优化后PCB板电子元件条件热布局的温度值最高稳态温度值稳定在82.613 ℃,最低稳态温度值为65.942 ℃,平均稳态温度值为70.981 ℃。

2.2 最大最小蚂蚁系统仿真结果

由图2可以看出,通过蚁群算法对PCB板电子元件条件热布局进行优化,结果的最优值说明在PCB板电子元件的最优布置情况从左到右的排序序号为:s14,s3,s1,s4,s9,s15,s16,s2,s12,s10,s13,s11,s6,s8,s7,s5,即应该将电子元件s14安装在C1位置处、电子元件s3安装在C2位置处、……、电子元件s5安装在C16处,此时通过优化可得到PCB板上电子元件形成的温度场中的最低温度值。采用最大最小蚂蚁系统仿真,按照此布局对PCB板电子元件重新建模,保持其他条件不变,模拟结果如图4所示。由图4可知,最高温度值为87.41 ℃,显示在C16位置处,最低温度值为72.75 ℃,显示在C8位置处,其平均值为81.21 ℃。经过多次迭代后可以看出,优化后温度场分布位于边缘位置处的温度值相对低一些。

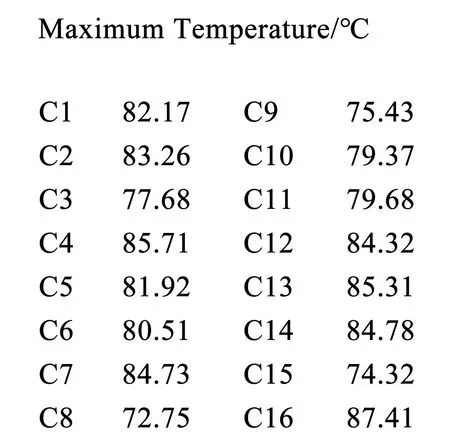
图4 最大最小蚂蚁系统仿真优化结果Fig.4 Simulation and optimization results of max-min Ant system

2.3 优化前后结果对比

采用传统的数学模型和ANSYS对PCB板电子元件条件热布局的温度结果进行计算,得到PCB板电子元件条件热布局优化前后的温度值,如表1、表2所示。

表1 数学模型的热布局节点温度值对比

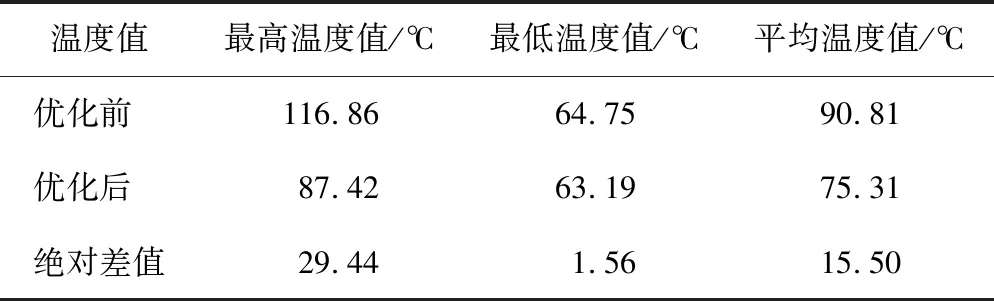
表2 ANSYS算法的热布局节点温度值对比

由表1、表2、可以看出,经过智能优化算法处理后的温度值得到了一定程度的降低,在工程应用中可采用蚁群算对电路板上的电子元件布局方式进行优化,为PCB板电子元件条件热布局提供借鉴参考。

3 结束语

智能优化算法在热布局优化中具有良好的适用性和有效性,能够有效解决复杂的优化问题。仿真分析在验证优化算法有效性和评估不同布局方案优劣方面起到了关键作用,为实际应用提供了理论支持和技术指导。