基于Anand 模型的BGA 封装热冲击循环分析及焊点疲劳寿命预测*

张惟斌，申坤,，姚颂禹,，江启峰

（1.西华大学流体及动力机械教育部重点实验室，成都 610039；2.西华大学能源与动力工程学院，成都 610039）

0 引言

电子元器件高可靠、长寿命要求的不断提高和电子技术的不断发展对电子元器件内部氛围以及环境要求越来越高[1]。在电子设备制造过程中，电子元器件封装是最关键的环节，它涉及到元器件与印刷电路板（PCB）之间的连接、散热以及保护等功能[2]。要提高电子元器件可靠性，关键在于控制电子元器件封装内部条件，所用材料与元器件所处的环境等时刻影响着封装内部的温度分布和热应力分布等[3]，为此需在基础研究和理论分析方面开展封装元器件内部瞬态、稳态温度分布和应力分布的研究，同时分析内部焊点疲劳寿命，为封装元器件的可靠运行提供研究基础。

目前，国内外许多专家学者对电子器件可靠性纷纷展开研究。李跃等[4]通过有限元计算，分析了PCB 整个组装板多器件焊点的残余应力应变分布，讨论出各焊点的危险位置以及热循环寿命。苏佩琳等[5]对PCB焊点热循环失效方式进行了分析和改进设计，通过在芯片边角下加锡块，使其最大等效塑性应变显著降低。张跃平[6]研究了封装结构温循载荷下的力学响应，为封装结构的损伤评估提供了重要技术手段。ZHOU等[7]通过扫面电镜和有限元分析，发现焊点的失效裂纹是由塑性功和蠕变应变累积引起的。

本文基于Anand 模型对PCB 封装元件内部的局部应力应变分布进行仿真分析，并讨论局部各器件焊点的应力失效位置，同时基于能量法的Darveaux 模型对焊点疲劳寿命进行预测[8]，将其与热冲击试验的寿命结果进行对比分析，为封装元器件内部结构精细化设计与改型奠定基础。

1 有限元计算模型的建立

1.1 三维几何模型

本文研究的某型三维封装存储器件模块中有5 个芯片，芯片由塑封料（即环氧树脂）包裹，放置在基板上，基板由焊球焊接在PCB 上。根据封装元件内部零部件的尺寸和相对位置建立封装元件的三维几何模型。建模采用UG 三维建模软件完成。建立的三维几何模型及局部模型如图1、2 所示。

图1 封装元件整体几何模型外部轮廓

图2 封装元件侧视剖视图及局部图

组成封装元件的主要材料有单晶硅（芯片）、环氧树脂、树脂（PCB、基板、底板）、SAC 305（焊球的主要焊锡料）、镍（镀镍膜）以及金（镀金膜）。其中，SAC 305 作为高精密电子元器件常用的无铅焊材，具有助焊剂兼容性好、高可焊性和扩展性等特点。

1.2 Anand 模型和材料性能

为了分析封装元件在热冲击下的内部应力分布，运用ANSYS 仿真模拟软件对器件进行有限元分析。采用Anand 黏塑性模型对焊料的非弹性率相关的变形行为进行分析。

Anand 模型将需要测定的材料非弹性流动的相关各向同性抗力用变量s 来表示（s 被称为变形抗力），以塑性状态变量输出，非弹性应变的输出为塑性应变。流动方程可写为

式中εin表示有效非弹性变形速率，A 为指数因数，Q为激活能，R 表示普适气体常数，T 表示绝对温度，ξ 表示应力系数，σ 表示有效Cauchy 应力，m 为应变率敏感指数。

本文需要测定的锡球材料为SAC305，其Anand模型参数设置见表1[5]，表中s0表示初始变形阻抗系数，h0表示硬化系数，表示变形阻力饱和值系数，n 表示饱和值的应变率敏感度，α 表示强化系数的应变率敏感度。环氧树脂、玻璃、金、镍的主要性能参数见表2。

表1 SAC305 Anand 模型参数

表2 各材料主要性能

1.3 三维网格划分

将绘制好的三维几何模型进行有限元网格划分。其节点数为1169340，单元数为458251。由于封装元件模型的复杂性，整体数值计算需要数量庞大的结构网格，计算资源无法满足，而网格数量过少会导致计算结果出现局部应力集中。为了降低网格质量对应力模拟结果误差的影响，本文截取封装元件内部最容易失效的部分作为代表模型进行精细网格计算，该局部模型既具有上层芯片和锡球，又具有下层芯片和锡球，受力情况复杂，具有代表性。模型的有限元计算网格数约为21×105个，如图3所示。为了增加计算结果的精确性，同时对焊点处进行网格加密、对单个焊点进行六面体网格划分。

图3 局部封装元件及内部锡球网格模型

1.4 温度边界条件

在热冲击极限循环试验中，设定单个循环的参数：0 s 时的初始温度为-65 ℃。此时假定封装元件内是温度平衡的，不考虑残余应力。温度变化设置：在0～120 s，维持-65 ℃；在120～130 s，由-65 ℃线性升高到150 ℃；在130～250 s，保持150 ℃[9]。

2 计算结果与分析

通过将温度载荷加载到局部模型的有限元网格上，基于Anand 黏塑性模型和Darveaux 模型，运用ANSYS 仿真软件进行模拟，得到在单个热冲击循环下的BGA 封装元件内部温度分布、应力和应变分布，并根据应变数据计算寿命。

2.1 热冲击极限试验温度场模拟结果

为了研究封装元件在热冲击试验下的内部失效机理，对局部最易失效部分的温度场进行分析，结果如图4 所示。可以看出温度从表面到内部逐渐减小，同时温度呈现对称分布，温度场呈现分层状态。250 s 时封装元件表面处温度最高，为150 ℃，最小温度在封装元件中部，为134.09 ℃，最大温差约为15 ℃。

2.2 热冲击极限试验应力应变模拟结果

对封装元件表面的细微变形量进行分析，变形分布见图5。可以得到最大变形为0.038 mm，最大变形位置为外侧镀膜处，变形表现为局部封装元件上凸。

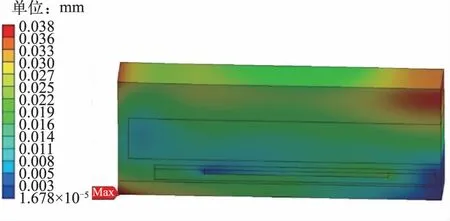
图5 局部模型变形分布

进一步探究热冲击对应力分布的影响以及应力最大值随时间的变化特性，结果分别如图6、7 所示。不难看出应力最大值出现在下层芯片上，最大值为222.18 MPa，其余部分应力值较小，均在20 MPa 以内，说明下层芯片及其焊点在热冲击下所受的影响较大，承受了较大应力，在设计时应该着重考虑该部分材料的应变率、应变硬化等特征。同时，下层芯片整体所受应力值随热冲击试验时间的增加而增大，并在120 s左右达到最大值，其值为222.18 MPa，随后逐渐下降，最终稳定在200 MPa 左右。

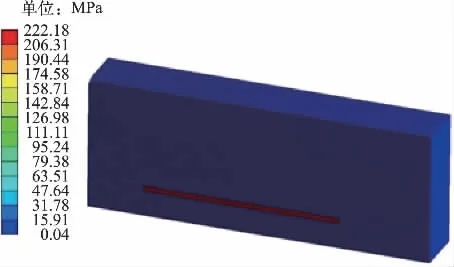
图6 局部模型应力分布

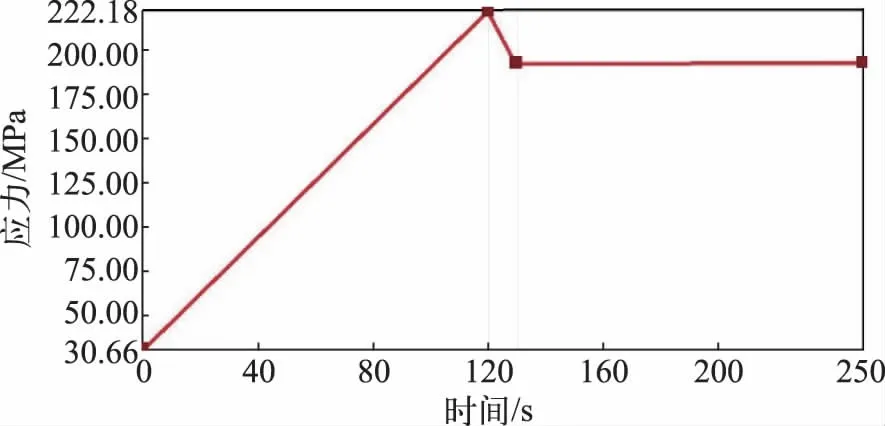
图7 应力最大值随时间变化情况

2.3 锡球应力应变分布

考虑到锡球作为主要的疲劳破坏危险部件，采用考虑材料黏塑性的Anand 模型对锡球部分进行仿真模拟。

锡球阵列的应变分布见图8（a）。同一排的每个锡球应变变化规律大致相同，均为两端的应变程度大于中间应变程度。对比同一排的锡球变形程度，可见中间区域的锡球变形量小于两端区域的锡球变形量，单个锡球最大变形量为0.43×10-3mm。锡球应力分布见图8（b），最大应力为19.02 MPa（250 s），应力最大位置在锡球下方边缘。锡球最大应力随时间变化曲线见图9，随着时间的变化，单个锡球最大应力在120 s 前不稳定，在120 s 前后所受应力达到最大值（21.08 MPa），之后应力逐渐平缓并最终稳定在8.00 MPa 左右。

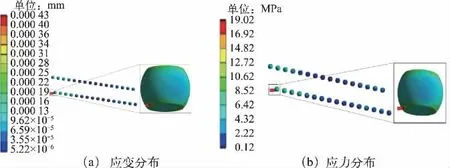
图8 锡球阵列的应力应变分布

图9 锡球最大应力随时间变化曲线

2.4 热冲击循环寿命预测及分析

采用基于能量法的Darveaux 模型，通过数值仿真计算获取封装元件焊点（锡球）在单个热冲击循环周期（0～250 s）内的最危险单元（最大应力位置）的塑性应变能密度，进而计算出最危险单元的裂纹萌生和裂纹扩展速率，在此基础上预测封装元件最危险单元（最大应力位置）的疲劳寿命。

Darveaux 模型中关于裂纹产生和裂纹扩展的方程式为

式中N0为裂纹萌生时经历的周期数；Nf为危险点的特征疲劳失效寿命，即失效率为63.2%时经历的周期数；a 为断裂特征长度，在这里取芯片危险单元与树脂的连接长度；da/dN 为裂纹扩展速率；ΔWi表示体积为vi的第i 个单元的塑性应变能密度；ΔWave为2 个循环的累计平均塑性应变能密度之差；K1、K2、K3和K4为裂纹扩展常数，K1=22 400，K2=-1.52，K3=1.488 44×10-5，K4=0.98[10-11]。

根据数值仿真结果，提取锡球上相关危险区域数值，其中a=0.01 mm，ΔWave=8.77×10-7mJ/mm3，危险单元的边长为0.021 mm，最危险单元的体积为1.81×10-6mm3，代入Darveaux 寿命预测公式，计算可得到在-65 ℃～150 ℃热冲击下的疲劳寿命预测结果，N0为2 032 次，Nf为2 176 次，按一个热冲击循环周次为250 s 计算，运行至6.29 天时出现疲劳失效。对元件进行热冲击试验，在试验第7 天出现破裂，元件破坏情况如图10 所示，破坏位置在外壳棱边中部，表现为内容物溢出。该试验失效天数与仿真结果基本一致。

图10 热冲击循环试验破裂元件

3 结论

本文针对给定封装元件开展三维几何建模、结构网格划分，进行温度分布、结构应力和应变的有限元计算及疲劳寿命预测，结论如下。

1）单个热冲击循环中，封装元件温度分布在空间上呈近似对称的形态。250 s 时封装元件的表面温度最高，为150 ℃，表面温度和内部中心温度存在15 ℃左右的温差。

2）单个热冲击循环中，封装元件最大变形量为0.038 mm（250 s），位置在外侧镀膜处，变形表现为封装元件上凸。最大应力值出现在下层芯片上，最大值为222.18 MPa（120 s），其余部分应力值均较小，在20 MPa 左右。其中，锡球上的最大应力为19.02 MPa，最大变形为0.43×10-3mm。

根据封装元件中锡球在最危险位置处裂纹萌生时的热冲击循环周次、特征疲劳寿命以及单个热冲击循环周次时间计算，预估的出现特征疲劳失效的时间和试验结果基本一致，证明了仿真分析和疲劳寿命预测的有效性。