面向天线跟踪系统的ADRC控制器设计及参数优化
张 越,范书瑞,郎利影
(1.河北工业大学 人工智能与数据科学学院,天津 300401;2.河北工业大学 电子与信息工程学院,天津 300401;3.河北工业大学创新研究院(石家庄),石家庄 050299)
0 引 言
永磁同步电机(permanent magnet synchronous motor,简称PMSM)以其高效率和高功率因数等优点,在工业和民用领域得到了广泛的应用[1]。然而,PMSM具有非线性、多变量强耦合性等特点,传统的滑模控制[3]和模糊PID控制器等控制方法在电机参数发生变化和外界负载变化导致内外扰动时,逐渐难以满足更高精度的控制要求。
自抗扰控制技术(active disturbance rejection control,简称ADRC)因其不依赖于被控对象的数学模型、鲁棒性强等优点而得到了广泛应用。使用ADRC控制器替换PID控制器来控制PMSM,可以提高控制效果[4],但ADRC控制器待整定参数多,这限制了ADRC控制器的使用范围。针对此问题,猴群优化算法[6]和飞蛾扑火优化算法[7]等应运而生,文献[8]为了提高优化算法的效果,通过指定寻优范围,提高了参数整定效果和控制器的鲁棒性。这些优化算法虽然降低了ADRC控制器参数整定难度,但并没有改变传统ADRC控制器的固有缺陷。因此,文献[9]使用神经网络中的sigmoid函数并代替了自抗扰控制器中的fal函数,使系统拥有了更好的动态性能和抗干扰性能。针对光电跟踪系统干扰问题,文献[10]提出了一种新的模糊自校正观测器结构来解决传统ESO在抗扰能力和噪声衰减能力之间的冲突问题。文献[11]将ADRC控制器用于双轴伺服转台跟踪,并改进了微分跟踪器,提高了其噪声衰减性能。文献[12]针对机载卫星跟踪系统,提出了一种带预测因子扩张状态观测器,提高了跟踪系统鲁棒性。
综上所述,ADRC的应用已经比较成熟,为了提高控制器性能,本文提出了一种新的fal函数使其增益在拐点处变化更加平滑,且此函数只有一个待整定参数,减少了ADRC控制器待整定参数,为了降低控制器参数整定难度,采用粒子群优化算法(PSO)对ADRC参数进行整定,通过仿真实验分析,改进的小误差自抗扰控制器具有更高的控制精度,更强的抗干扰能力,更快的响应速度以及更小的超调量。
1 ADRC控制器设计
1.1 伺服系统建模
伺服系统是天线跟踪系统的机械部分,伺服系统的控制精度与天线跟踪精度密切相关。本文对表贴式PMSM进行建模,根据矢量控制理论建立基于d,q坐标系的PMSM数学模型,如下所示[13-14]:
(1)
式中:id和iq为d轴与q轴电流;θm为转子空间电角度;ωe为电角速度;ωm为转子角度;J为转动惯量;B为粘滞摩擦系数;TL为转矩负载;Rs为定子电阻;Ld和Lq为等效的d轴与q轴电感;ψr为永磁体磁链;Te为电磁转矩;p为电机极对数。
在同步旋转坐标系下,使用id=0的控制策略,上述PMSM数学模型可以简化:
(2)
为了使天线对准卫星,需要通过卫星位置得到伺服系统目标俯仰角和航向角。假设地球为均匀球体,地面站位置经纬度为(XM,YM),由于跟踪卫星为同步卫星,其经纬度为(XS,0),则可以得到北半球位置(XM,YM)下伺服系统指向俯仰角和方位角的计算式,与式(1)、式(2)相结合,可以得到如下跟踪模型:
(3)
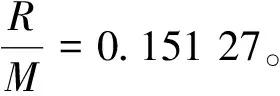
1.2 控制器设计
ADRC控制器主要由微分跟踪器(tracking differentiator,简称TD),非线性误差控制器(non-linear state error feedback,简称NLSEF),以及非线性扩张状态观测器(non-linear extended state observer,简称NESO)3部分构成。本文使用的ADRC控制器结构框图如图1所示。

图1 自抗扰控制器结构框图
1.2.1 微分跟踪器
跟踪微分器理论上相当于非线性滤波器[15]。二阶离散系统的跟踪微分器形式如下:
(4)
式中:r1(k+1),r2(k+1)分别为k+1时刻输入信号的跟踪信号及其微分;r1(k),r2(k)分别为当前时刻输入信号的跟踪信号及其微分;r0用于调节跟踪速度;h为跟踪步长;h0为滤波因子;fc为最速控制综合函数。
1.2.2 非线性扩张状态观测器
(5)
式中:y(k)为控制系统k时刻位置输出;z1(k+1)为k+1时刻电机位置状态观测值,z2(k+1)为k+1时刻电机角速度的观测信号;z3(k+1)为k+1时刻总扰动的估计信号;z1(k),z2(k),z3(k)为对应观测信号k时刻的值;λ1,λ2,λ3为待整定的比例系数,其中fal函数为非线性函数。
1.2.3 非线性误差控制器
非线性误差控制器主要针对非线性状态观测器和微分跟踪器的输出得到各阶信号的误差信号[18],采用如下非线性控制率:
(6)
式中:ei为第i阶误差信号(i= 1,2);zi为ESO对状态的估计;ri为TD得到的跟踪信号以及跟踪信号的各阶导数;k1,α1,k2,α2为待整定系数;b为ESO中待调整参数;z3为ESO对总噪声的估计量;u为控制量。
2 fal函数改进
ADRC控制器中,虽然fal函数在定义域中是连续的,但其定义域内不光滑,可能导致控制量输出和观测值出现抖动[19],而且待整定参数多,设置困难。而采用fal函数的系统容易出现增益过大导致观测效果不佳的问题。因此提出了一种新的Le_fal函数:
(7)
式中:a为待整定系数;e为观测误差。Le_fal函数增益图如图2所示,误差增益图如图3所示。

图2 Le_fal增益图
由图2和图3可以看出,Le_fal函数的输出值的增加速度小于e的增加速度,实现了误差减小的目的,防止系统出现超调。当误差为0时,传统的fal函数在e在(-δ,δ)时,误差增益固定为恒值,而Le_fal函数的增益为有限值,Le_fal的输出大于e,实现了小误差放大的作用,如果在NESO中使用Le_fal函数,不仅可以简化整个控制系统,而且可以提高观测器的观测能力,进而提高控制系统的抗干扰能力。同时,在NLSEF中也使用Le_fal函数优化来原有的fal函数并提高控制器的稳定性。
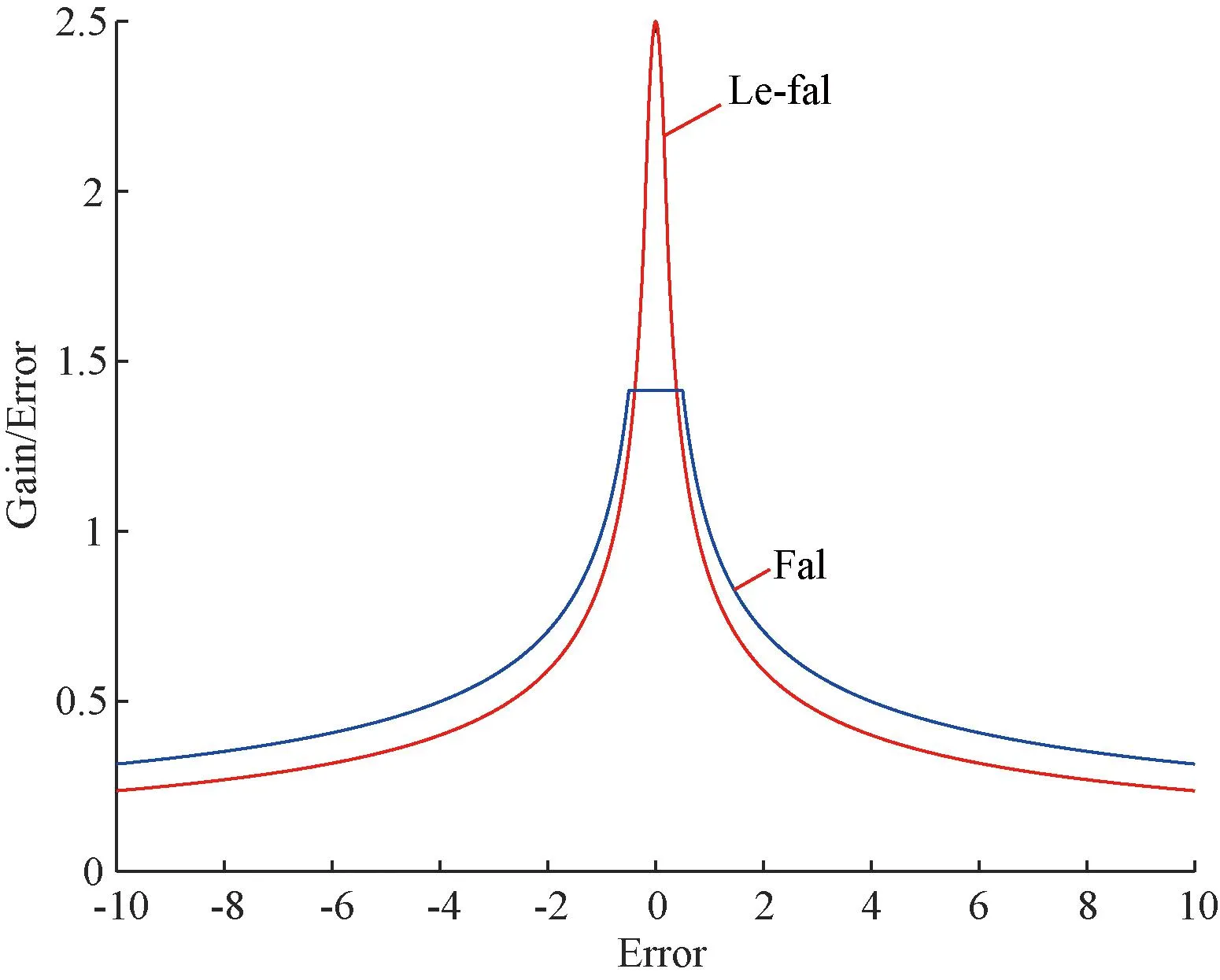
图3 Le_fal与Fal函数误差增益图
因此,可以得到改进后的离散化NESO公式:
(8)
式(8)中变量含义与式(5)相同。
同理,结合Le_fal函数的NLSEF数学模型如下:
(9)
式(9)中变量含义与式(6)相同。
改进后的ADRC控制器待整定参数为r0、h、h0、β1、β2、λ1、λ2、λ3、b及b0,以及ESO中的α1、α2和NLSEF中的α1、α2,相比于传统的ADRC控制器,待整定参数减少了4个。
3 基于粒子群算法的ADRC参数整定
粒子群算法源于对鸟群觅食行为的研究,鸟群通过集体信息共享使群体找到最优的目的地[20,21]。因此对ADRC控制器参数整定问题可以抽象为鸟类的觅食问题。
1)参数初始化
粒子群优化算法使用dim代表问题解的维度,使用brids代表种群个数,其中每个个体表示为i(i=1,2,3,…,brids),在算法寻优过程中brids保持不变,个体通过函数rand()对个体进行初始化。通过iters控制迭代次数,迭代完成之后通过适应度函数确定损失最小个体,本文设置个体维度dim=5,设定初始种群个数brids=20,iters=20,学习因子c1=1,c2=2,vmax=0.5。
2)更新粒子位置和速度
粒子群优化算法通过一定规则更新粒子的位置和速度,粒子的下一时刻速度需要根据当前最优个体和全局最优个体更新,具体更新规则如下所示:
veli=veli+c1rand(pbesti-psoi)+c2rand(gbest-psoi)
(10)
式中:veli是的第i个粒子的速度;pbesti是第i个粒子的历史最优位置;gbest是当前时刻所有粒子的全局最优位置;rand()产生(0,1)区间内的随机数;c1是个体加速度系数;c2是群体加速度系数。
为了防止粒子速度过大设置第i个粒子的速度veli如下所示“
veli=min(max(veli,-vmax),vmax)
(11)
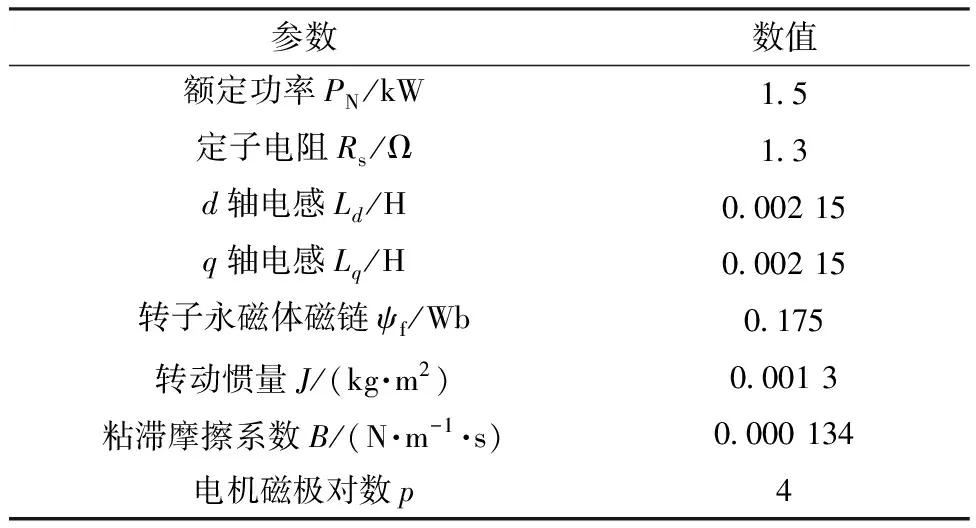
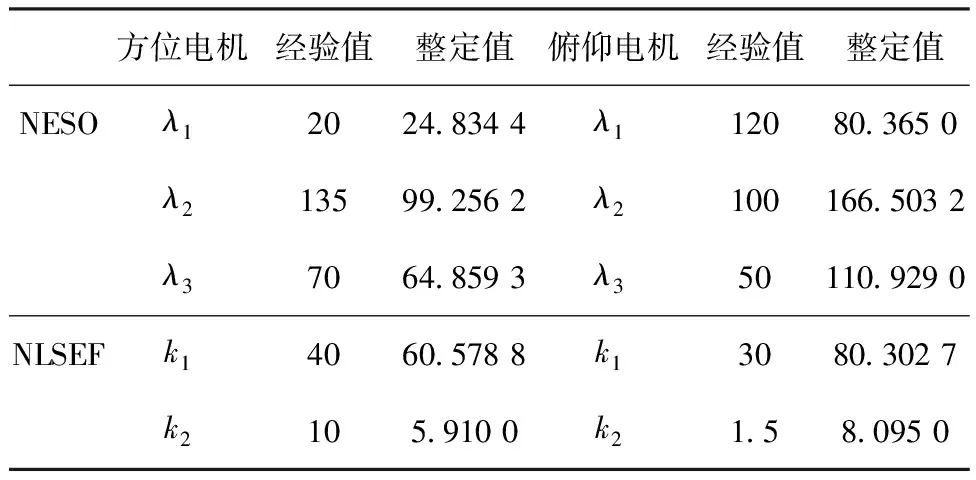
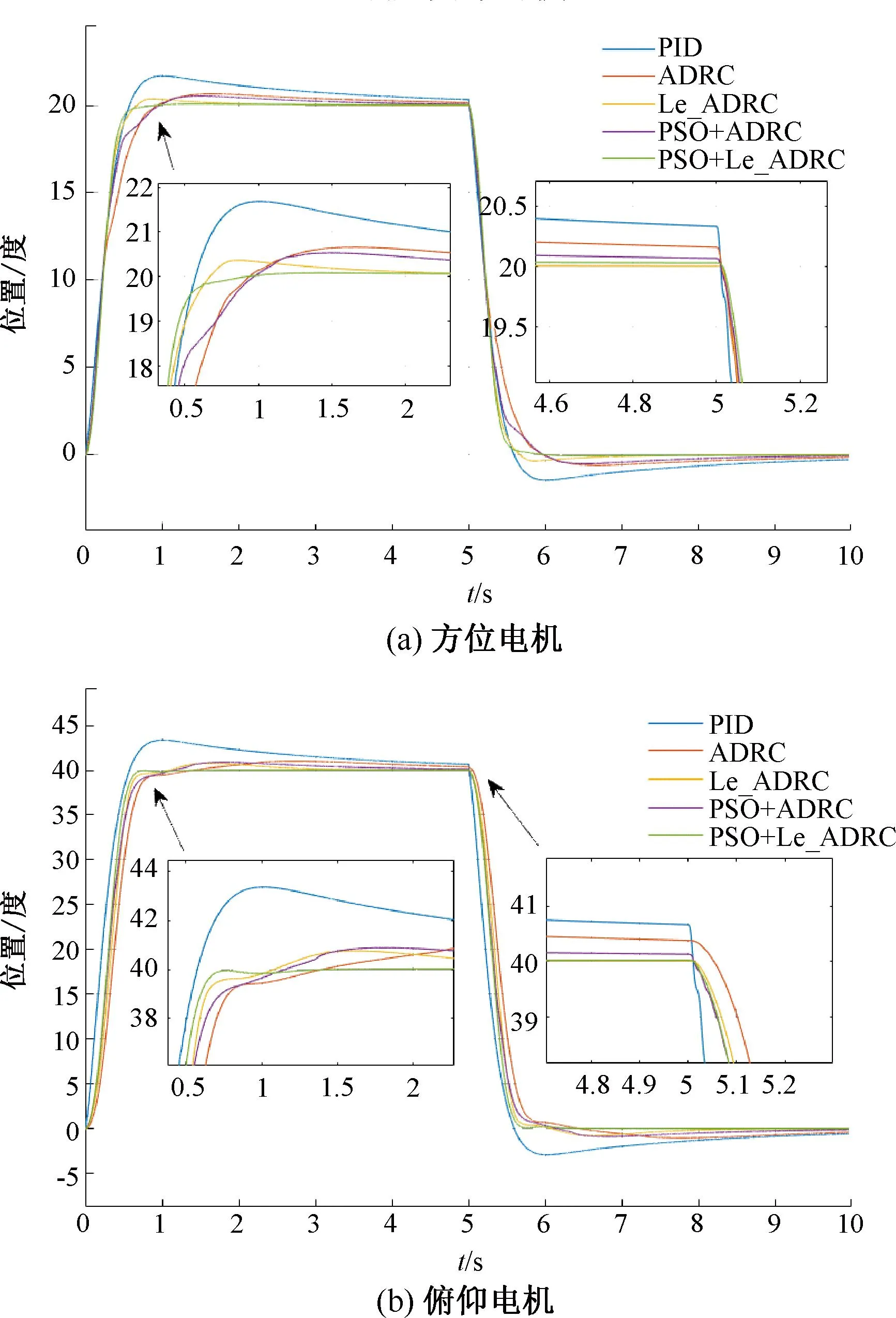
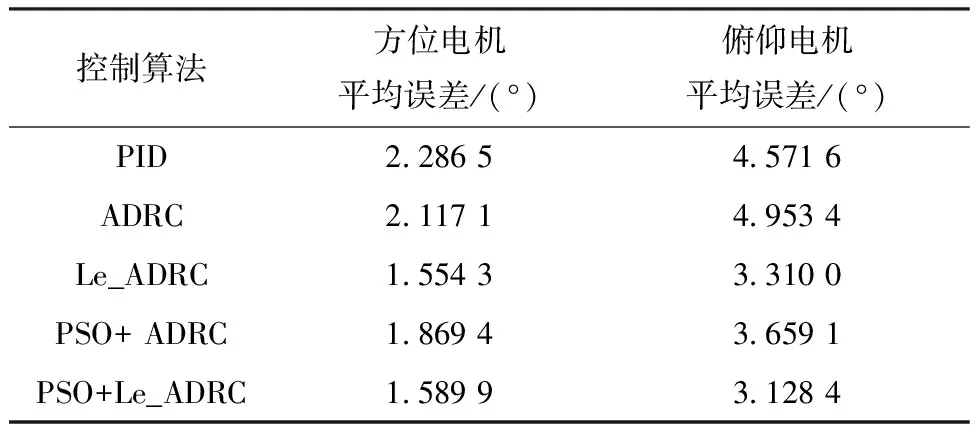
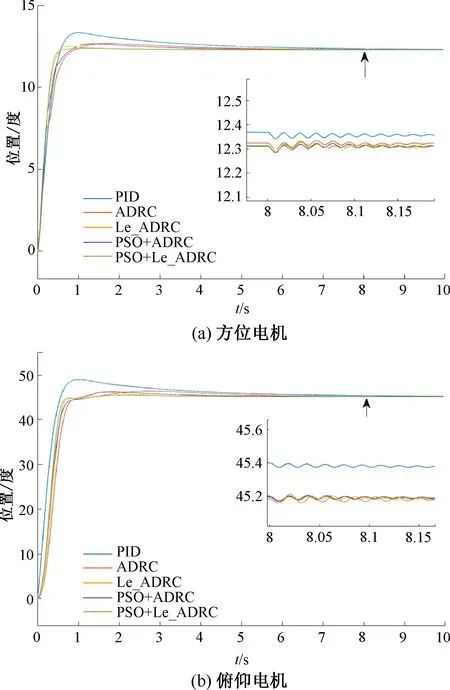
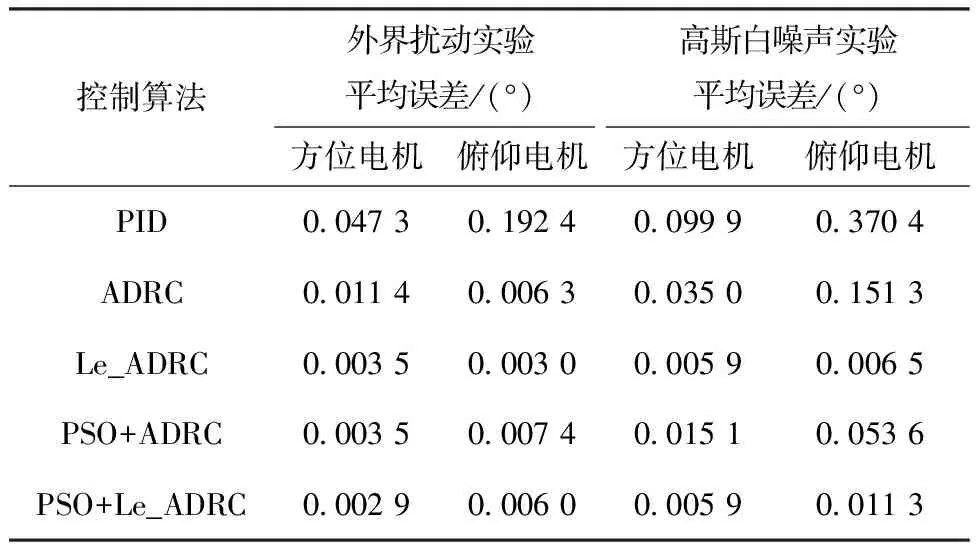
式中:vmax为粒子速度最大值。最终粒子速度-vmax 因此粒子的位置更新公式: psoi=psoi+veli (12) 即第i个粒子下一时刻的位置为当前位置psoi与当前速度veli之和。 综合考虑控制器的快速性、精确性和稳定性,本文的适应度函数采用超调量σ,调节时间ts,峰值时间tp,上升时间tr,稳态误差e构造适应度函数,其具体形式: values=k1ts+k2tp+k3tr+k4e+k5σ (13) 式中:k1,k2,k3,k4,k5分别为权重系数。本文重点关注ADRC控制器的稳态误差、超调量和调节时间参数,因此这里设置k1=k4=k5=2,k2=k3=1。 3)ADRC参数整定 针对ADRC控制器中NESO和NLSEF模块的β1、β2、λ1、λ2、λ3进行参数整定,种群初始化公式如下: pso=1+(300-1)rand(brids,dim) (14) 式中:pso为初始化后的种群。分别对方位电机和俯仰电机Le_ADRC控制器、ADRC控制器参数进行整定,Le_ADRC控制器参数整定适应度变化如图4所示。 由图4可以看出,控制器参数优化在到达20次迭代后适应度值基本保持不变,ADRC控制器的粒子群参数整定与此类似,故不作赘述。 假设跟踪系统坐标为(38°3′3.6″S,114°20′24.0″E),模拟对准卫星为亚洲四号,经纬度为(0°N,122°E)。由式(3)解算出当前俯仰电机目标角度约为45.18°,方位电机目标角度约为12.31°。永磁同步电机参数如表1所示。 表1 电机参数表 启动设置:初始俯仰电机负载设置为0.5 N·m,用于模拟天线负载,由于偏航电机的负载包括俯仰电机,因此设置偏航电机挂载1 N·m模拟总负载。具体控制器参数设置如下所示。 设置ADRC控制器参数NESO中,ε1=0.5,ε2=1,α1=α2=0.3。NLSEF中ε1=ε2=0.5,α1=0.5,α2=0.75,r0、h、h0、b及b0参数设置同Le_ADRC,针对Le_ADRC控制算法,本文设置r0=500,h=0.001,h0=0.01,由于α1与α2都小于1,这里令α1=0.5,α2=0.8,b0=b=10。通过粒子群优化算法整定参数设置如下。 表2 PID参数设置 表3 ADRC参数表 表4 Le_ADRC参数表 电机跟踪输入的响应,反映天线当前位置,5种算法控制下方位电机和俯仰电机的位置变化过程如图5所示。 图5 方位电机和俯仰电机位置响应曲线 以方位电机为例,由表5可以看出,PSO+Le_ADRC算法超调量为0.377 5%,调节时间为0.47 s,稳态误差为0.016 2,各项性能指标表现总体优于其它控制器。 表5 方位电机位置响应仿真结果对比表 跟踪稳定性实验是对设置期望跟踪方位的跟踪性能进行分析,采用幅值分别为20和40、周期为10 s、占空比为50%的方波信号,分别对方位电机和俯仰电机跟踪性能测试,观察各个控制器的跟踪性能,跟踪结果图6所示。 由图6可见,PSO+Le_ADRC能够快速收敛到目标位置。以第一部分方波为例,计算方位电机超调量为0.45%,调节时间为0.543 s,俯仰电机超调量为0.75%,调节时间为0.615 s。 图6 方位电机和俯仰电机方波跟踪曲线 图7 方位电机(左)和俯仰电机(右)正弦波跟踪曲线 计算得出方位电机和俯仰电机各控制下的正弦曲线平均跟踪误差,结果如表6所示。可以看出,PSO+Le_ADRC跟踪性能优于其他控制器。 表6 正弦曲线跟踪实验结果对比表 假设伺服系统已经控制天线到达指定位置,在8 s处受到一个外界扰动,模拟作用大小为1 N·m的负载扰动,控制器控制效果如图8所示。 图8 方位电机和俯仰仰电机负载干扰实验 为了模拟系统工作过程中系统参数变化等干扰,引入幅值为0.005°/Hz,采样时间为0.1 s的高斯白噪声模拟以上因素对系统带来的影响,控制器控制效果如图9所示。 在负载干扰实验中,为了衡量扰动对输出的影响,计算8.0~8.5 s的平均误差,在高斯白噪声实验中,由于PID控制器调节时间最长,则认为PID控制器输出进入0.02°误差带内所有控制器都进入稳态,从此时开始计算平均误差,实验结果如表7所示,可以看出,PSO+Le_ADRC控制器抗干扰性能优于其他控制器。 表7 抗干扰仿真实验结果对比表 本文对自抗扰控制技术进行了介绍,设计了基于永磁同步电机的自抗扰控制器,针对传统自抗扰控制器fal函数存在高频抖动的问题,提出了一种新的Le_fal函数优化原有的fal函数。将改进后的Le_ADRC与PID和传统的ADRC控制方法进行对比,实验结果表明,Le_ADRC具有超调量小,响应速度快,稳态误差小,抗干扰能力强等优点。针对Le_ADRC参数难整定的问题,采用粒子群优化算法进行参数整定,实验结果表明,粒子群优化算法能较好地完成参数整定工作,为自抗扰控制器的工程应用提供了参考。4 实验与结果分析

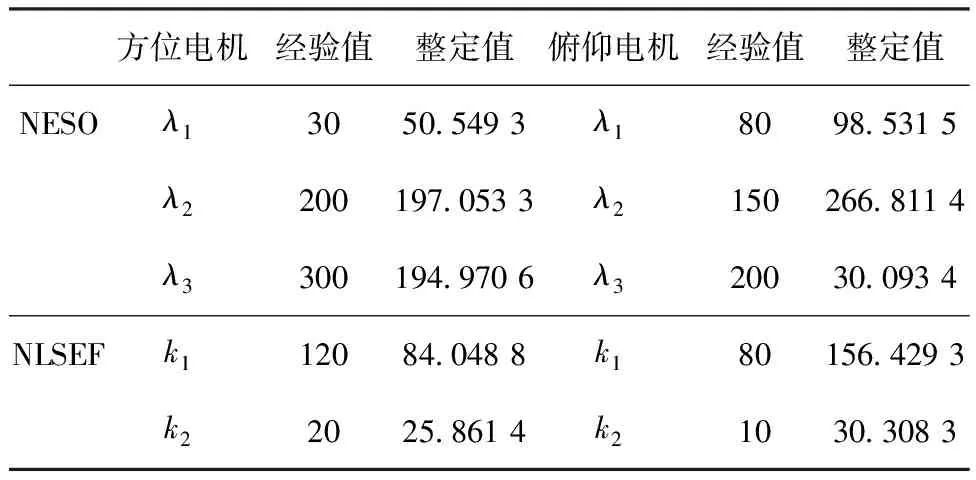
4.1 位置仿真实验

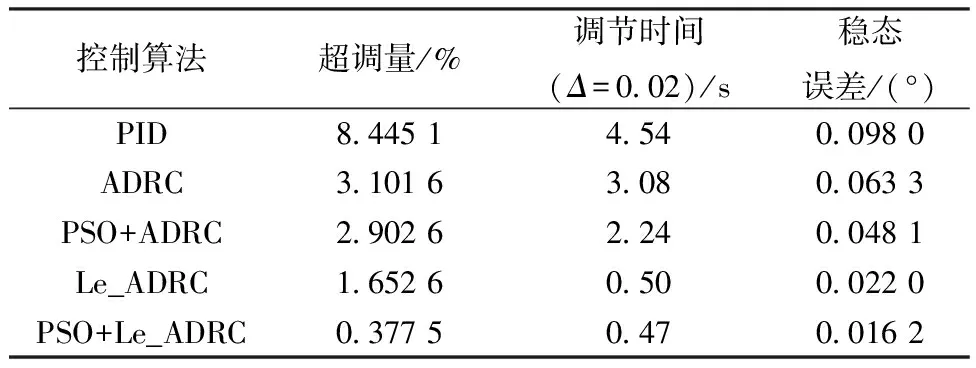
4.2 跟踪稳定性仿真实验

4.3 抗干扰仿真实验
5 结 语

