基于佳点集-t分布变异的麻雀算法VSG控制策略研究

闫丽梅,洪益民,王登银,郭建祎,赖 胜

(1.东北石油大学 电气信息工程学院,大庆 163318;2.河南电力调度控制中心,郑州 450000)

0 引 言

“碳达峰,碳中和”目标的提出,推动了以风电、光伏为代表的可再生新能源在电网中的广泛应用。光伏和风电等新能源发电一般通过响应快、控制灵活的电力电子变换器并入交流微电网,但变换器不同于传统发电机,其缺少惯性和阻尼,这就导致变换器抑制电网波动和干扰的能力较差。高比例新能源并网会造成一系列问题,为解决这些问题,虚拟同步发电机(以下简称VSG)控制策略[1-2]被国内外学者们相继提出。

VSG控制参数众多,传统的参数计算过程较为繁琐,无法同时优化多个参数,且当出现给定功率扰动或电网频率扰动时,不良参数控制的VSG会出现输出功率超限和频率振荡的问题。而将VSG与优化算法进行结合,可以简化VSG的参数优化过程,并且能够解决不良参数控制时出现的超限和振荡问题。根据该思路,一系列的改进措施被提出:文献[3]将模糊算法与VSG控制策略相结合,优化了转动惯量的调节过程,但模糊算法中的模糊规则和隶属度函数是科研人员根据经验给定的;文献[4]在控制系统中引入天牛群优化算法,降低了负荷波动时对电网的冲击,且维持住频率的稳定;文献[5]提出天牛群优化算法,借助该算法计算出VSG的最佳惯量和阻尼参数,从而解决了频率振荡和输出功率超限等问题;文献[6]中最优虚拟惯量值通过粒子群优化算法 (PSO) 获得,但并未对阻尼进行计算和分析。为进一步优化VSG在给定有功扰动或电网频率突变扰动时存在的问题,本文提出了一种基于佳点集-t分布变异的麻雀算法VSG控制策略,利用其最优化求解VSG的核心参数。

1 VSG基本原理及控制策略

1.1 VSG电路模型

VSG控制策略是一种新型的微电网逆变控制策略,主要是通过改进逆变器接口来模拟同步发电机特性,以达到与同步发电机输出特性相似的效果。图1为典型VSG控制策略方案。方案中测量装置、常规VSG控制器和电压、电流双环控制属于基础部分,此外方案中还包含储能系统、LCL滤波器、分布式电源及三相逆变器。VSG的运行过程:调度指令输出的有功参考值Pref、无功参考值Qref,与测量装置输出的瞬时有功值Pout、无功功率值Qout一同输入到VSG控制器中,经控制器计算后得到输出电压的功角θ及幅值E;然后输出电压经双环控制处理后输出控制信号,该信号经SPWM脉宽调制后用来控制逆变系统中开关管的开通与关断,从而模拟出同步发电机的输出功率特性[7]。

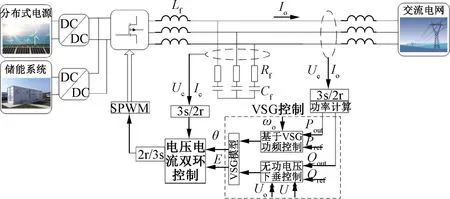
图1 VSG拓扑

1.2 有功-频率控制和无功-电压控制

图2为经典VSG有功-频率控制器结构框图,发电机的机械特性由控制器中的有功-频率环节模拟。

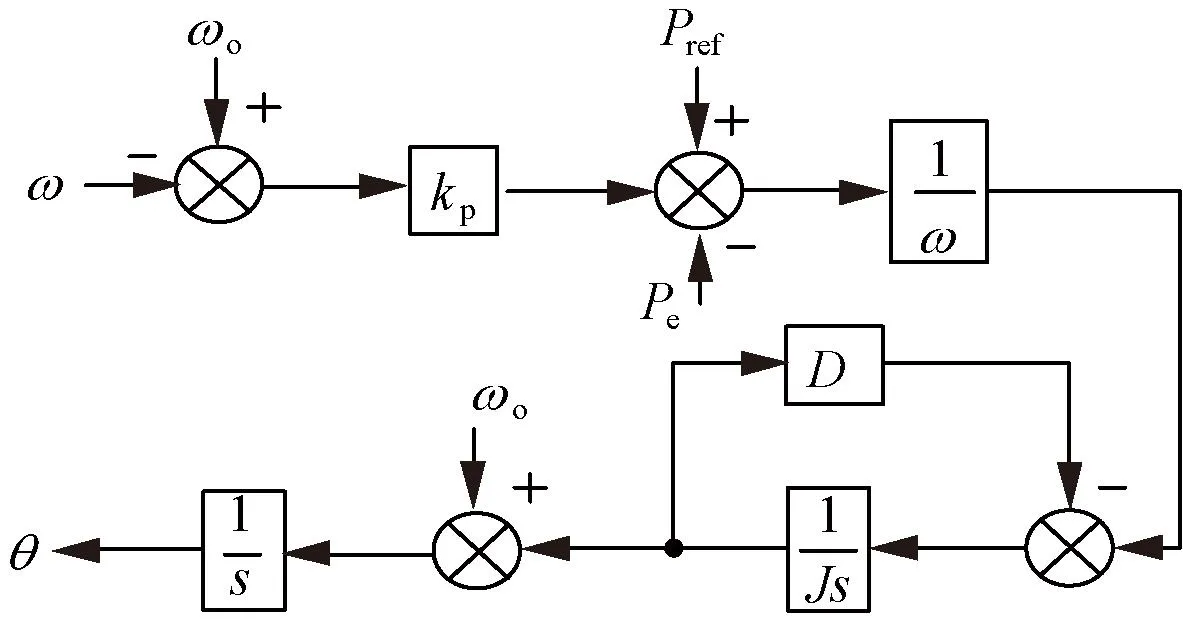
图2 VSG有功-频率控制器结构框图

图3为经典VSG无功-电压控制器结构框图,其主要作用是模拟同步发电机的励磁器。

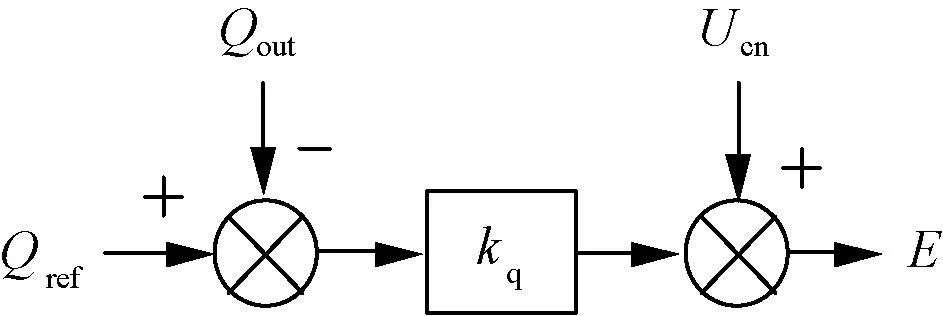
图3 VSG无功-电压控制器结构框图

2 改进麻雀搜索算法

麻雀搜索算法(以下简称SSA) 是近期提出的优化算法[8]。该算法的局部搜索和全局搜索主要是通过模拟麻雀群体的觅食和反捕食习惯来实现的,算法寻优过程即麻雀种群觅食的过程。SSA寻优能力好,鲁棒性强,但迭代后期易陷入局部最优,且收敛过程中存在速度慢等的问题,针对这些问题,本文提出了改进ISSA算法。首先,利用佳点集对麻雀种群进行初始化,提升了种群的多样性和稳定性;然后将正态分布引入发现者位置更新公式中,加快收敛速度,并协调全局探索和局部挖掘的能力;最后在麻雀个体位置更新后引入自适应t分布变异策略,避免算法陷入局部最优。

2.1 佳点集

基本SSA通过随机方式初始化种群,这种方式生成的种群会有较大的差异性,搜索空间的环境信息利用效果不显著。目前,Logistic混沌映射[6]、Piecewise混沌映射[10]和Tent混沌映射[11]等混沌映射方法常被用来解决种群初始化问题,混沌映射能解决种群分布不均的问题,但混沌映射每次产生的种群分布是随机的,会造成种群初始化的随机性。因此本节通过引入均匀性和稳定性更强的佳点集来初始化种群。

佳点集由华罗庚等提出,文献[12]的研究已经证实其用于智能算法上具有优越性,通过其生成的种群分布均匀,增加了种群的多样性。图4为包含200个二维点的初始种群分布图。由图4可知,在同样的取点个数下,佳点集法相较于其他两种方法取点分布更均匀,且佳点集更稳定,只要种群数目不变,每次的取点分布效果都是一样的,因佳点集的构造和维数无关,这种优势并不仅存在于低维空间,在高维问题中同样适用。

图4 二维初始种群分布图

2.2 基于正态分布的发现者搜索策略改进

(1)

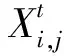
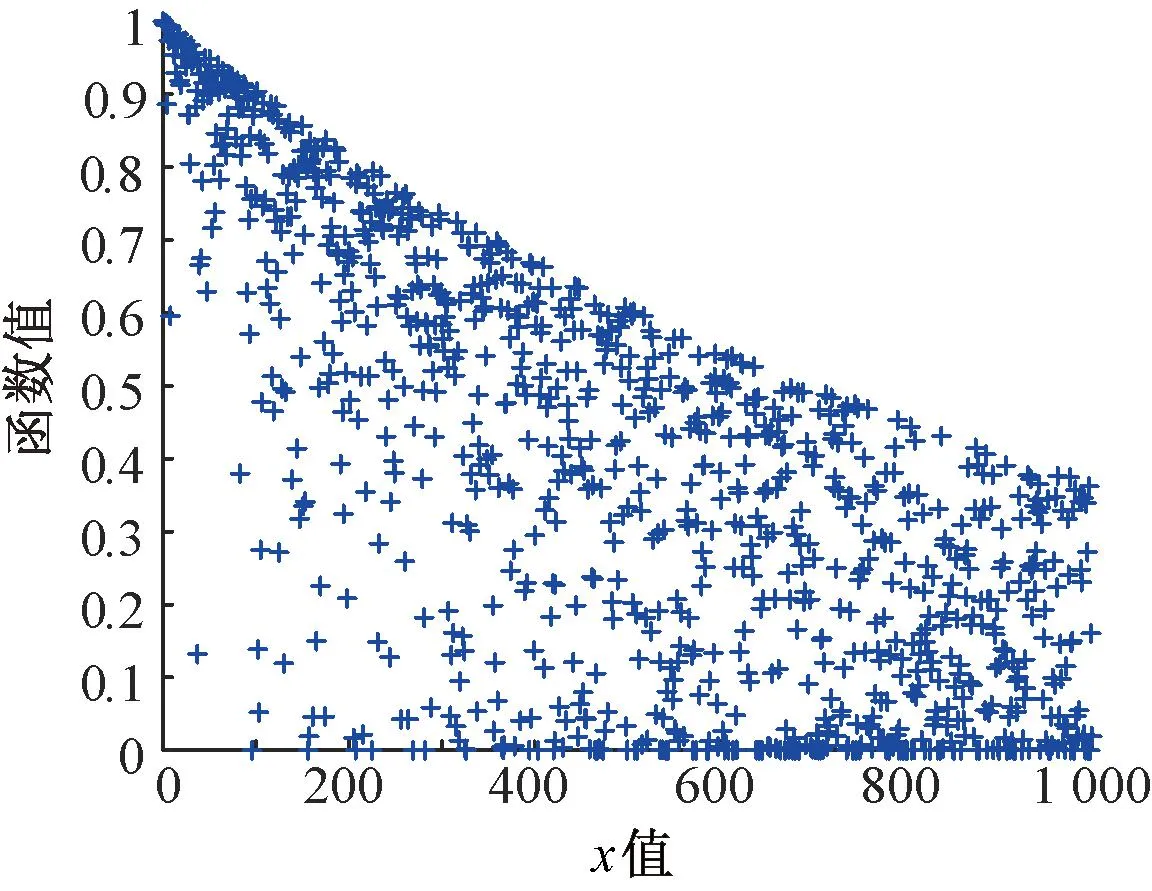
图5 改进前发现者搜索策略

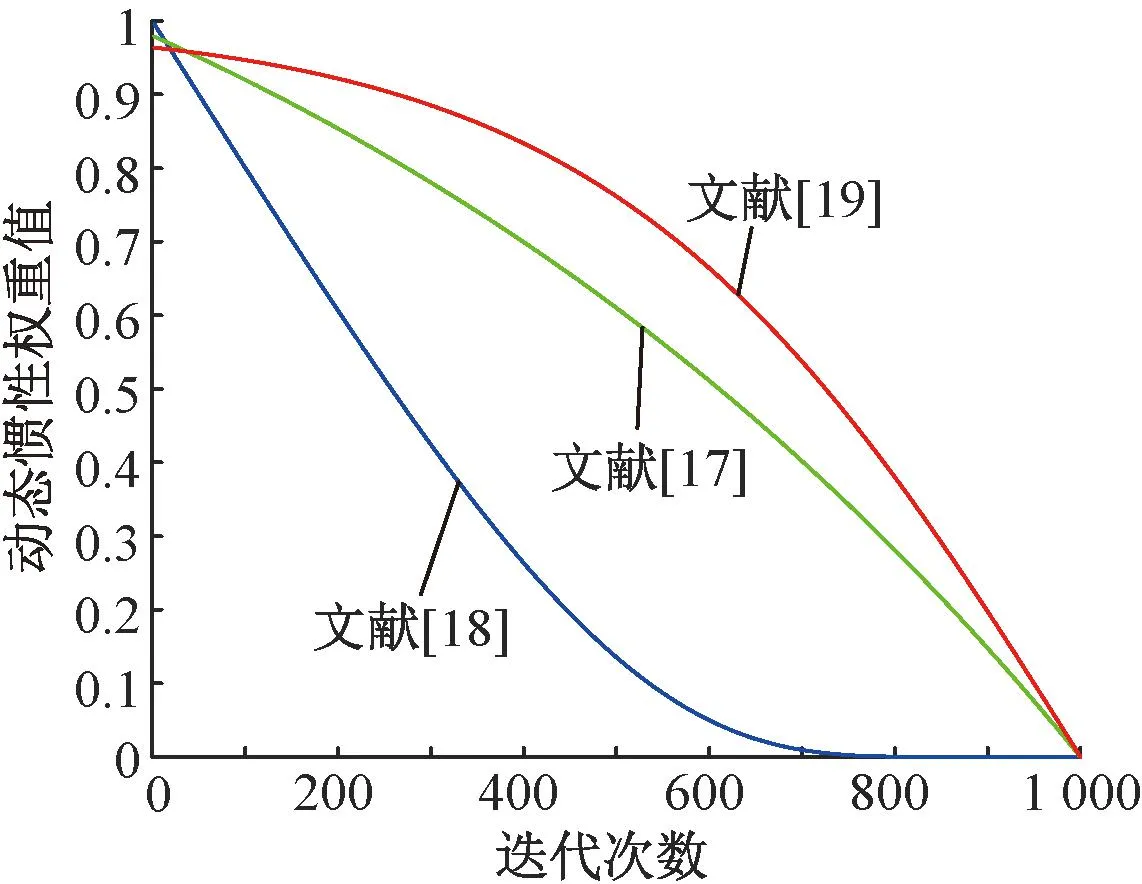
图6 惯性权重因子变化曲线

图8为改进后的发现者策略。引进正态分布后发现者的搜索范围得到了拓展,改善了算法对最优解处于非原点问题的收敛性能。

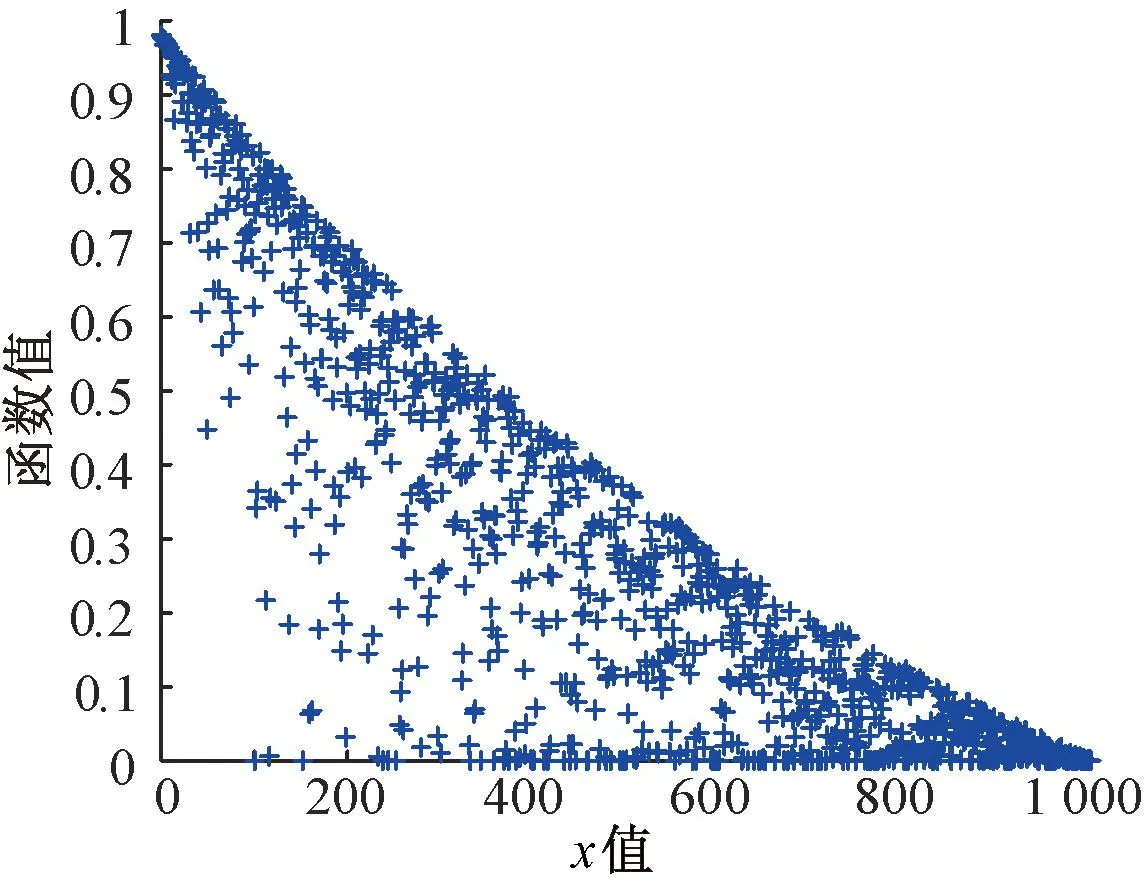
图7 文献[13]的发现者搜索策略

图8 改进后发现者搜索策略

2.3 自适应t分布变异

麻雀算法中引入自适应t分布变异策略[17],对每次迭代更新后的位置xi进行自适应t分布变异,可以避免算法陷入局部最优,变异公式如下:

(2)

自适应t分布变异的自由度参数为算法的迭代次数T,当T值较小时,t分布变异效果相当于柯西分布变异。图9为柯西分布在值域在[-100,100]的函数散点图。由图9可知,柯西分布易生成一个离原点较远的随机数,此时变异项t(T)·xi会形成较大的扰动,算法具有较强的全局探索能力,利于算法跳出局部最优。算法中期,t变异处于俩分布变异之中。在算法后期,T值较大,t分布变异相当于高斯分布变异。图10为高斯分布的函数散点图。高斯分布产生的随机数离原点较近,变异项的作用较小,算法开始细致的局部搜索,能够改善其收敛精度和速度,获得良好的局部开发能力。

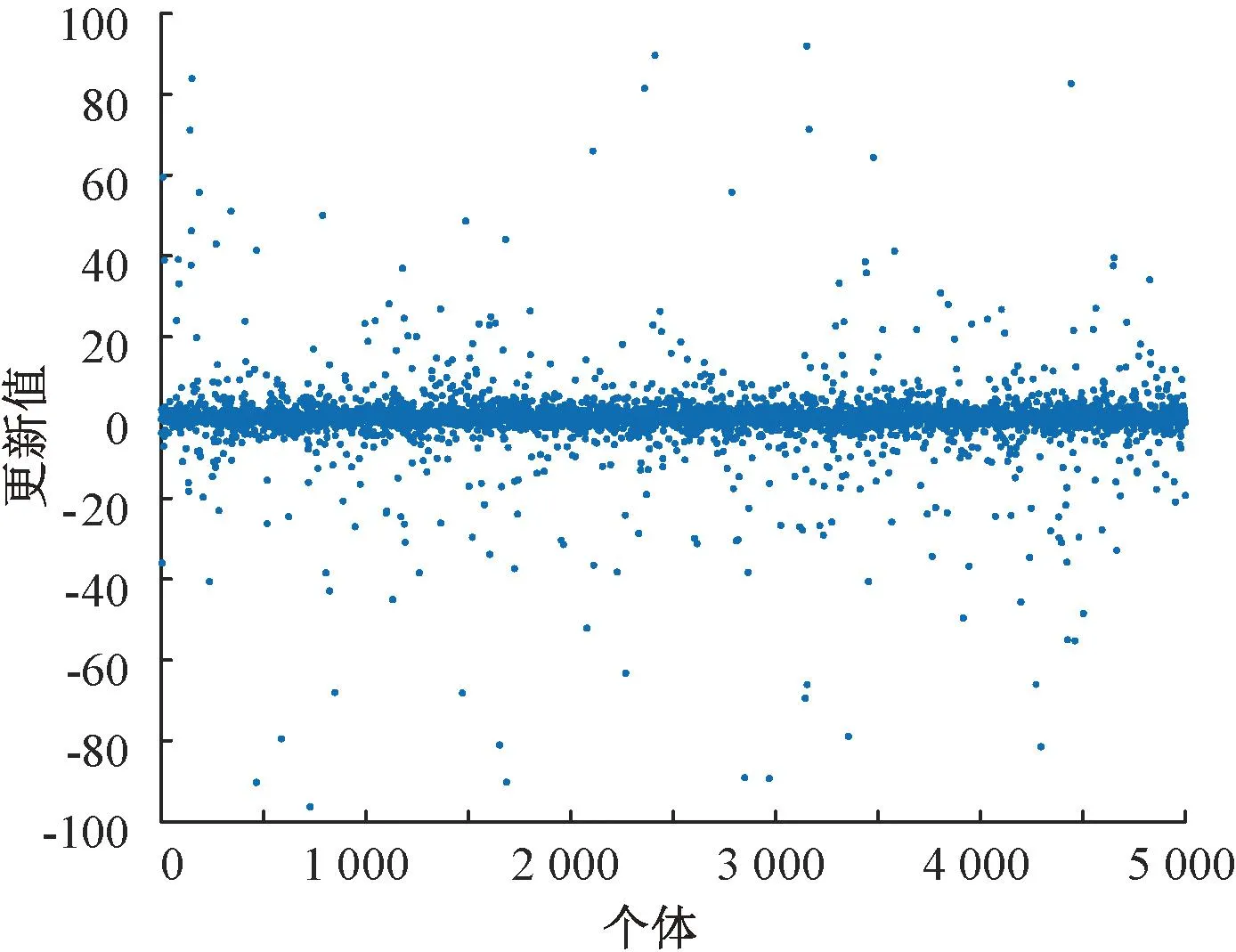
图9 柯西分布函数散点图

图10 高斯分布的函数散点图

因此,t分布变异同时拥有这两种分布的优点,引入t分布变异对算法的局部开发能力和全局探索能力都有较大的提升。

通过上述算法改进,能够增强算法的全局探索能力和局部开发能力,但无法确定变异前后麻雀个体的适应度值的优劣,因此在算法中加入贪婪规则。该规则能够比较变异前后麻雀个体的适应度值,以判断是否需要更新麻雀个体的位置。贪婪规则[15]如下式:

(3)

2.4 算法测试实验

选取12个难度不一的函数,通过改进麻雀搜索算法(以下简称ISSA),测试这些函数的收敛速度及精度,来检验ISSA的可行性和寻优性,同时与SSA、粒子群算法(PSO)[18]、鲸鱼优化算法(WOA)[19]、萤火虫算法(FA)[20]4种算法进行对比,以检验ISSA收敛速度和精度的优劣。测试函数收敛曲线如附录所示。由附录图1可知,ISSA算法在单峰、多峰测试函数中都具有很好的稳定性和适用性,相比于其它算法具有更好的收敛精度及寻优能力,验证了ISSA的有效性和可行性。

3 基于ISSA的VSG控制

3.1 适应度函数设计

ISSA具有较优的寻优能力,将该算法与VSG控制相结合。适应度通常用于评价麻雀个体位置的优劣,能够影响算法的搜索方向、收敛速度,甚至决定算法是否寻得最优解。本文采用一个加权函数作为优化VSG系统的性能指标,该加权函数由总谐波畸变率(THD)和误差绝对值乘以时间项对时间的积分(ITAE)组成。THD和ITAE的表达式[21]如下:

(4)

式中:e(t)为输出误差;U1n为输出电压基波幅值;Uon为输出电压谐波幅值。

适应度函数表达式:

(5)

式中:a,b为常数,用于控制ITAE和THD在函数中的占比;Δid和Δiq为d轴和q轴上并网侧电感电流的误差。

当适应度值满足最优条件时,令ISSA产生一组解,将这组解赋值给VSG中的各个参数。

图11为ISSA的VSG控制过程。图12为基于优化算法的VSG拓扑。

图11 基于ISSA的VSG参数优化流程图

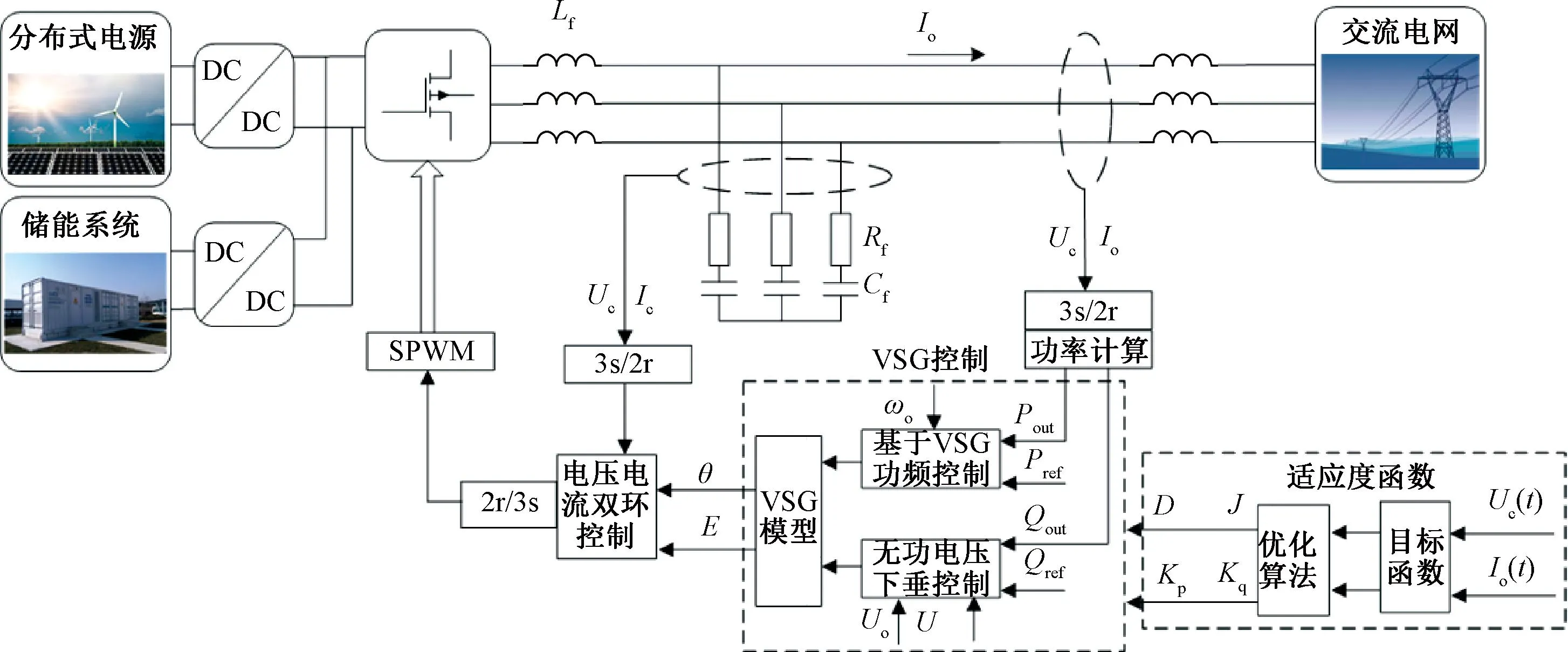
图12 基于优化算法的VSG拓扑

3.2 VSG 参数设计

表1为系统主电路相关参数。

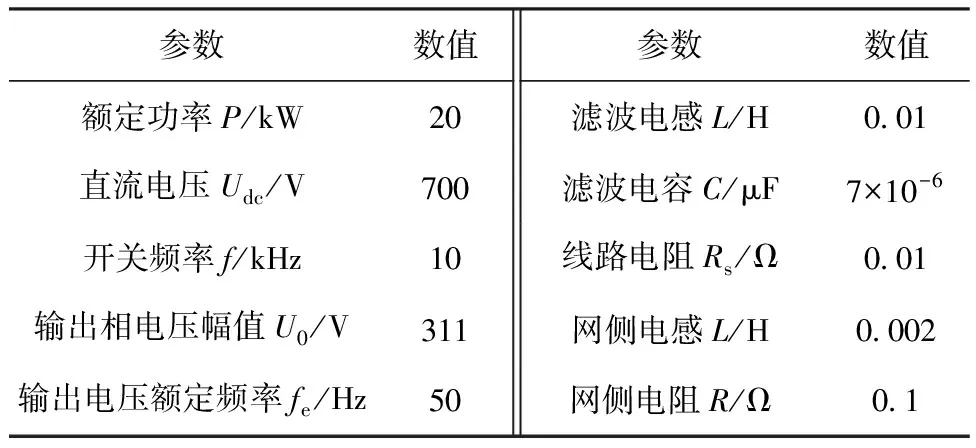
表1 系统主电路参数表

由图2和图3可知,除了表1中的参数外,还需设计阻尼系数D、虚拟转动惯量J、时间常数τ以及有功、无功下垂系数KP、Kq等参数[22-23]。

阻尼系数D定义为所需求的转矩与角速度两者改变量的比值,其表达式:

(6)

式中:J按J=τ×D选取,τ一般取为0.04。

KP定义为角速度改变量与有功功率改变量的比值,即:

(7)

Kq定义为电压改变量与无功功率改变量的比值,即:

(8)

由表1可知,VSG的额定功率值为20 kW,要求系统有功功率和无功功率变化均为100%(20 kW和20 kVar),电网电压幅值及电网频率变化分别为10%和0.5%。计算可得参数如表2所示。

表2 传统VSG系统控制参数

4 仿真分析

4.1 参数设置

为能够更好得对比传统VSG、SSA优化的VSG及ISSA优化的VSG这三者的优劣,本文利用MATLAB/Simulink搭建了这三者的仿真模型。为保证性能对比的准确性,均采用表1的系统主电路参数以及图1的拓扑结构。对于需实施优化的核心控制参数,传统VSG模型采用表2中的参数进行仿真,SSA和ISSA优化下的VSG模型通过各自的优化流程后得到优化参数进行仿真。SSA和ISSA算法运行参数如表3所示。

表3 SSA和ISSA优化算法的运行参数

4.2 给定有功扰动仿真

在实际应用中,VSG的给定有功指令Pref通常由接入系统的光伏或风电的发电量决定,因此该值会有波动。为了验证改进算法在实际应用中Pref变化时控制情况,在维持电网频率50 Hz和电压幅值311 V稳定的情况下,仿真设置连续给定有功指令:当t=0.3 s时,将给定有功功率从10 kW提升至15 kW,当t=1.5时,将给定有功功率从15 kW下降至12 kW。

采用表3运行参数开始仿真,图13为算法运行后的适应度曲线。由图13可知,在迭代次数内两种优化算法均能收敛,且ISSA算法的收敛速度和精度都要优于SSA,显然ISSA算法的寻优能力更好。经过算法优化得到的参数如表4所示。

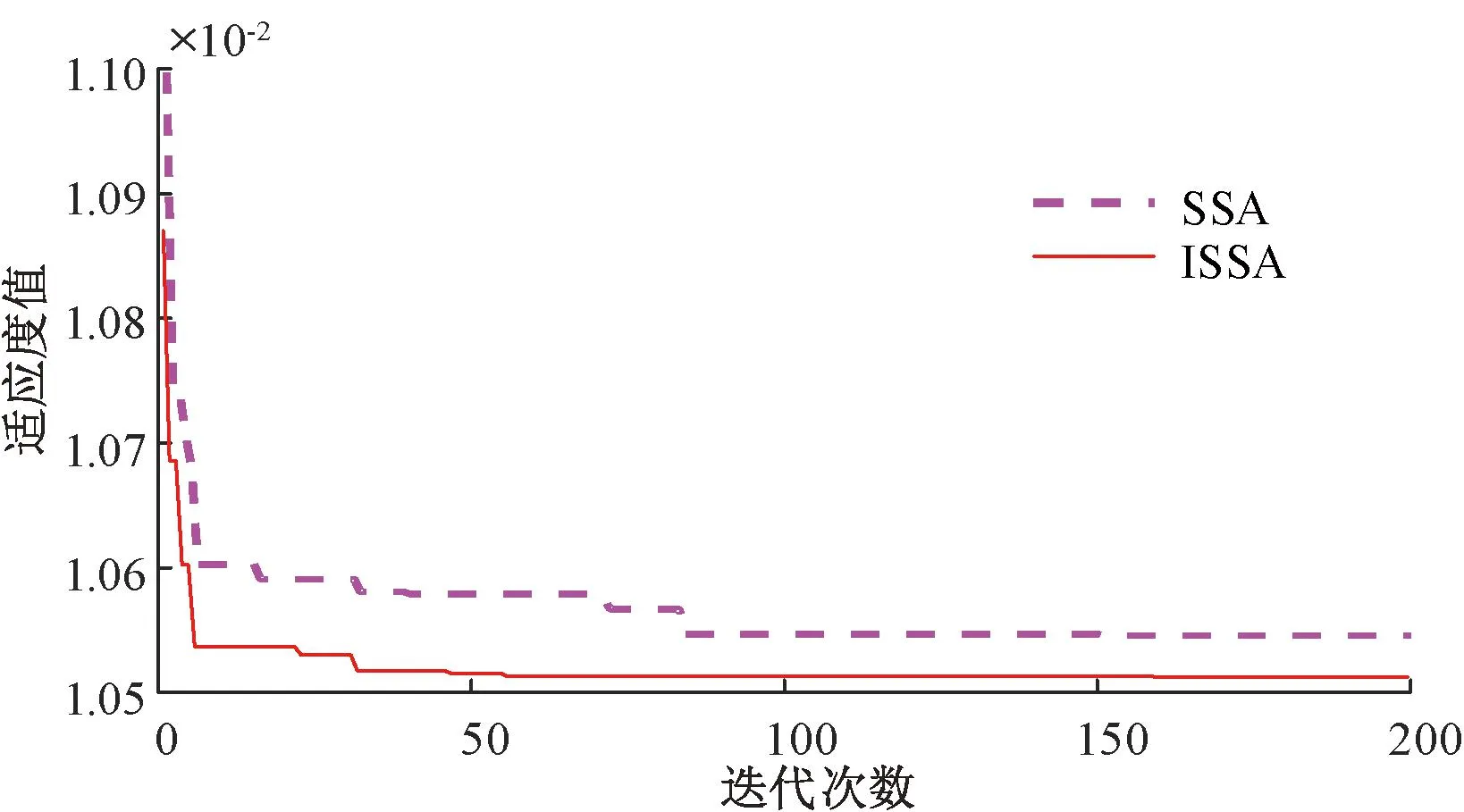
图13 适应度函数曲线

常规VSG采用表2的控制参数,SSA算法和ISSA算法采用表4的控制参数。三种控制方式有功功率、频率仿真对比如图14所示。

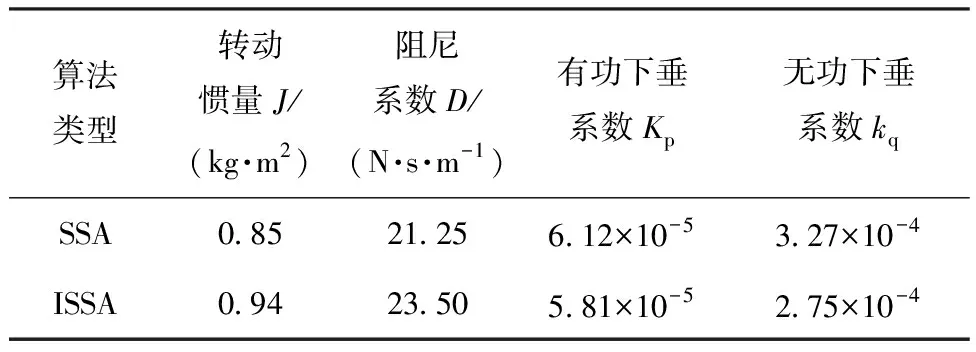
表4 SSA和ISSA优化算法结果

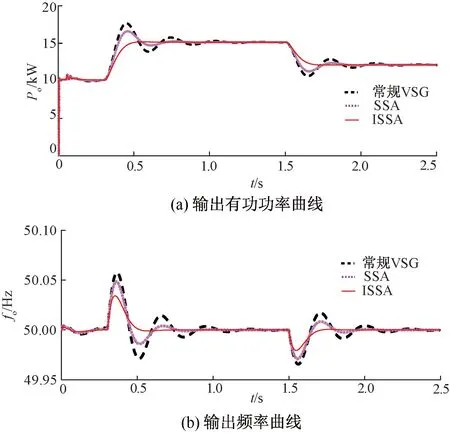
图14 给定有功扰动情况下三种控制方式的有功功率、频率仿真对比

由图14可知,当给定功率变化时,常规VSG有功功率振荡次数为4次,最大超调量为16.8%,调节时间为0.66 s,最大频率偏差和调节时间分别为0.057 Hz和0.88 s;SSA算法有功功率振荡次数为2次,最大超调量为9.6%,调节时间为0.36 s,最大频率偏差和调节时间分别为0.048 Hz和0.61 s;ISSA优化算法有功功率振荡次数为0,最大超调量为0.11%,调节时间为0.26 s,最大频率偏差和调节时间分别为0.034 Hz和0.29 s。

通过仿真波形对比可知,在给定功率变化时,本文提出的ISSA算法优化后的VSG,其具有更小的功率振荡幅度和频率偏差,以及更快的调节速度,对提高VSG系统输出功率的稳定性要优于另外两种方法。

4.3 电网频率突变扰动仿真

在仿真中分别设置电网频率上升和频率下降两种扰动。扰动1在t=0.5 s时,电网频率从50 Hz上升至50.1 Hz;扰动2在t=0.5 s时,电网频率比从50 Hz下降至49.9 Hz。常规VSG、SSA算法和ISSA算法的控制参数和情况一相同。电网频率突变扰动输出波形对比如图15所示。

图15 电网频率突变扰动输出波形对比

由图15可知,电网频率上升扰动阶段,常规VSG最大频率偏差和所需调整时间分别为0.15 Hz和0.65 s;SSA算法最大频率偏差和所需调整时间分别为0.128 Hz和0.38 s;ISSA优化算法最大频率偏差和所需调整时间分别为0.114 Hz和0.29 s。在电网频率下降扰动阶段,常规VSG最大频率偏差和所需调整时间分别为0.138 Hz和0.38 s;SSA算法最大频率偏差和所需调整时间分别为0.116 Hz和0.296 s;ISSA优化算法最大频率偏差和所需调整时间分别为0.104 Hz和0.19 s。

通过波形对比可知,在电网频率突变扰动时,相较于常规VSG和SSA算法,本文提出的ISSA算法的控制策略,能够有效地降低突变引起的最大频率偏移量,且能快速将频率恢复至额定值,对电网频率突变干扰有较好的应对能力。

5 结 语

常规的VSG技术通过模拟传统同步发电机的转动惯量和阻尼,大大增强了变换器抑制波动和干扰的能力,但常规的VSG技术存在着给定功率突变时导致系统频率和输出功率产生振荡以及电网频率突变扰动时频率偏差过大,调节时间过长等问题。针对上述问题,本文提出了一种基于佳点集和t分布变异的改进麻雀优化算法VSG控制策略来解决上述问题,并通过仿真验证了该控制策略的有效性,结论如下:

在传统麻雀算法中引入佳点集、正态分布和自适应t分布变异,构建出ISSA算法模型,利用ISSA算法对VSG系统参数进行优化,并与常规VSG和SSA算法进行对比分析。通过仿真对比可知,当系统出现给定有功功率扰动和电网频率突变扰动时,优化的ISSA算法控制策略能够抑制振荡,缩短调节时间,且能有效地减小输出频率和功率的超调量,进一步提高了系统的稳定性。