计及电动汽车移动储能动态电价的微电网优化调度研究

陈洪亮,徐海博,孙瑞雪

(1.沈阳卓立新能源技术有限公司,辽宁 沈阳 110027;2.国网辽宁省电力有限公司实业分公司,辽宁 沈阳 110059)

0 引言

“双碳”目标下,利用电动汽车(electric vehicle,EV)移动储能特性可提高微电网灵活性。EV作为一种移动储能装置,若进行有效控制,参与微电网的优化调度,与新能源协调运行,可提高微电网稳定性与经济性[1-2]。因此,亟需对考虑EV的微电网优化调度方法进行深入研究。

目前,关于EV接入微电网稳定性问题,相关学者做了一定研究。文献[3]建立以锂电池作为储能装置的全寿命周期成本模型,未利用EV集群提高微电网运行水平。文献[4]针对新能源出力的波动性提出EV参与度和效用函数最大的EV运行模型,设计了一种基于一致性理论的EV充放电功率分布式控制方法。文献[5]提出一种风光储多能互补微电网系统日前调度优化模型。文献[6]建立总运行费用与总网损最小的微电网多目标随机动态优化调度模型。文献[7-8]建立考虑热电联产机组及环境成本的微电网经济调度模型,通过蓄电池储能降低微电网的综合运行成本。但上述文献未考虑将EV作为储能装置研究其充放电双向行为对微电网经济调度的影响。

针对上述内容,以下文献通过电价引导EV参与微电网储能并激励用户参与微电网调度。文献[9]中EV充电电价采用居民用电峰谷分时电价,激励更多用户参与微电网调度,但目标函数中未考虑EV电池损失成本。文献[10]通过研究EV用户对电价变化的需求响应,提出引导EV充电的最优峰谷电价定价方案,但会出现反调峰现象。文献[11]分析分时电价对充电EV负荷转移概率的影响,均未考虑EV用户成本、电池损失成本。文献[12]根据电网预测调度目标提出考虑EV用户期望的定价策略,用户可按照自身需求选择充电时段。以上文献所提定价方法均基于EV用户需求响应及用户成本,未考虑新能源出力对电价的影响。

鉴于上述问题,首先提出一种在动态电价机制下考虑EV移动储能的微电网调度模型。所提EV动态电价机制根据新能源预测功率得出各时段的充电电价,引导EV参与微电网调度。其次,建立考虑环境成本、微电网运行成本和EV用户成本最低目标的经济调度模型。最后,通过与传统无序充电对比分析互动,所提考虑EV移动储能的动态电价机制提升了微电网与EV用户经济效益,验证所提方法的有效性。

1 电动汽车接入微电网的调度结构

图1为微电网结构,微电网包含微电网能量管理系统、微电源及常规负荷,其中微电源由柴油发电机(diesel generators,DG)、风电机组(wind turbines,WT)、光伏发电系统(photovoltaic panels,PV)组成。EV接入微电网可减小对主网的电力需求,也可将EV作为移动储能来平衡微电网与常规负荷间的电力。

图1 微电网结构

微电网能量管理系统根据EV用户接入时间、电池信息及未来24 h源荷出力预测数据,向EV用户发布充电电价信息等待用户响应,参与微电网储能调节,并安排各微电源的出力。当微电网内部发电量无法消纳或供电不足时,微电网能量管理系统根据主网的购售电价通过联络线与主网进行能量交换。

a.PV模型

光伏发电输出功率表示为

(1)

(2)

式中:PPV为PV实际出力;PPV,STC为标准测试条件下最大功率;R、RSTC分别为实际光照强度值、标准测试条件下光照强度值;γ为功率温度系数;Ta、Tr、Tamb、TNOC分别为光伏单元实际温度、参照温度、环境温度和正常条件下光伏单元温度。

b.WT模型

风电机组输出功率为[13]

(3)

式中:PWT、PWT_rate分别为WT实际功率和额定功率;vci、vco、vr分别为机组切入风速、切出风速、额定风速,分别取3 m/s、25 m/s、14 m/s。

c.DG模型

柴油发电机的燃料消耗量是其输出功率的线性函数,即:

F=F0×PDG_rate+F1×PDG

(4)

式中:F为燃料消耗率;F0为截距系数;F1为斜率;PDG_rate为DG的额定功率;PDG为DG的实际功率。

d.EV动力电池充放电功率模型

EV充放电模型如下:

(5)

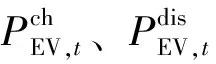
e.基于蒙特卡洛的EV无序充电模型

单个EV的充电行为由车主决定,具有较强的随机性。在大数据背景下,EV数据可经分析、归纳近似满足相应的概率分布,如式(6)、式(7)所示。EV出行数据来自美国交通部对全美车辆出行调查数据[13]。

EV起止充电时间服从正态分布,概率密度函数如式(6)所示。

(6)

式中:μs取17.6;σs取3.4。

日行驶距离近似服从对数正态分布,概率密度函数为

(7)

式中:μd取3.2;σd取0.88。

EV充电时长为

(8)

式中:TC为充电时间;S为日行驶距离;W100为耗电量;PC为充电功率。

通过蒙特卡洛法抽取每辆EV起始充电时间及日行驶距离得出每辆EV的充电时长,计算单辆EV充电负荷,之后对充电负荷叠加,得到所有充电负荷。将1天分为24个时段,间隔1 h,可得出N辆EV每时段对应的充电负荷为

(9)

式中:Pj为第j个时段总充电负荷;N为EV数量;Pn,j为第n辆EV在第j个时段充电负荷。

采用蒙特卡洛法抽取单位EV起始充电时间、日行驶距离的计算方法,其流程如图2所示。

图2 基于蒙特卡洛模拟的EV充电负荷计算流程

对50辆EV进行100次模拟得到EV无序充电功率负荷曲线,如图3所示。

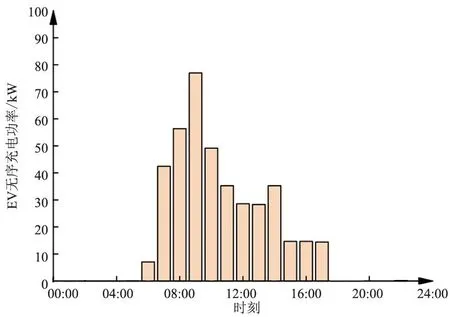
图3 EV无序充电功率

2 EV有序充电控制策略

本文通过电价激励控制EV有序充电,充分开发EV电池储能潜力,提出一种根据新能源出力大小制定EV动态充电电价的方法。文中所提考虑EV移动储能的动态充电电价同时兼顾EV用户成本与新能源出力大小,根据24 h内风电、光伏出力预测值与平均值计算EV各时段充电电价。文献[14-15]将风电、光伏出力划分为3个阶段,分别对应3个EV充电电价阶段(高、平、低),通过计算得到3个出力阶段的最大值、最小值相对平均值的波动范围为30%左右,由于文献[15]典型日出力数据与实际整体出力存在误差,文中风电、光伏出力波动范围取25%。风电、光伏出力超过其平均值的125%,EV充电电价低;低于其平均值的75%,EV充电电价高;在两者之间为平电价,高、低电价分别基于平电价上、下浮动60%。EV基准充电电价s0为居民用电三级电价,高、低、平充电电价阶段分别为1.253元/kWh、0.335元/kWh、0.781元/kWh。为便于计算,文中s0取0.8元/kWh,高、低、平分时电价取1.28元/kWh、0.8元/kWh、0.32元/kWh。

EV充电电价与风电、光伏预测功率关系如下:

(10)

(11)

利用各时段充电电价差将EV充电负荷转移到风电、光伏出力大的时段,具体流程见图4。

图4 动态充电电价流程

3 调度模型

3.1 目标函数

微电网综合运行成本主要考虑微电源运行成本、DG机组的燃料成本、电能交互成本、新能源发电补贴费用、环境成本、EV损失成本和调度成本,其优化调度模型的目标函数如下:

minf=min(CWT,t+CPV,t+CDG,t+CES,t+CS,t+

CSUB,t+CEV,t+CH,t)

(12)

式中:f为微电网综合运行成本;CWT,t为WT在t时刻运行成本;CPV,t为PV在t时刻运行成本;CDG,t为DG在t时刻运行成本;CES,t为EV损耗成本;CS,t为电能交互成本;CSUB,t为新能源发电补贴费用;CEV,t为EV调度成本;CH,t为环境成本。

a.微电源运行成本

CWT,t=MWT,t+DWT,t

(13)

CPV,t=MPV,t+DPV,t

(14)

CDG,t=MDG,t+DDG,t+Cfule

(15)

式中:MWT,t为WT在t时刻维修成本;MPV,t为PV在t时刻维修成本;MDG,t为DG在t时刻维修成本;DWT,t为WT在t时刻折旧费用;DPV,t为PV在t时刻折旧费用;DDG,t为DG在t时刻折旧费用;Cfule为柴油发电机燃料成本。

(16)

(17)

式中:Km,i为微电源单位运行维修费用;PWT,t为WT在t时刻出力;PPV,t为PV在t时刻出力;PDG,t为DG在t时刻出力;cins,t为微电源i的安装成本;Prate,t为微电源i的额定功率;fe,i为微电源i的容量因子;d为折旧系数;m为微电源的使用寿命。

b.DG燃料成本

柴油发电机的燃料成本数学表达式为

(18)

式中:α、β、γ为柴油发电机的燃料成本系数,取α=6,β=0.12,γ=8.5×10-4。

c.电能交互成本

微电网与主网进行电能交换时产生的费用由微电网购电成本和售电收益组成。当微电源出力不能满足负荷需求时,由于微电网向主网购电价格高,此时微电网系统通过动态充电电价引导EV放电;当EV放电不能满足负荷需求时,此时从主网购电。反之,当微电源出力除了满足自身负荷需求外仍有剩余,可引导EV充电或在售电价格高时向主网售电。与主网电能交互成本如下:

CS,t=Cbuy,t+Csell,t

(19)

(20)

式中:Pbuy,t、Psell,t分别为微电网向主网购、售电功率;cbuy,t、csell,t分别为微电网向主网购、售电价。

d.新能源发电补贴费用

Csub,t=csub(PWT,t+PPV,t)

(21)

式中:csub为分布式新能源发电补贴单价,取0.01元/kWh。

e.环境成本

常规发电污染物治理费用计为环境成本如下:

CH,t=PDG,t(aDGCO2σCO2+aDGSO2σSO2+aDGNOxσNOx)

(22)

式中:aDGCO2为柴油发电机CO2排放量;aDGSO2为柴油发电机SO2排放量;aDGNOx为柴油发电机NOx排放量;σCO2为CO2治理费用;σSO2为SO2治理费用;σNOx为NOx治理费用。

f.EV调度成本

充放电响应采用一定比例的充放电电价进行补偿,计算方式如下:

CEV,t=CEV_ch,t+CEV_dis,t

(23)

(24)

式中:CEV_ch,t、CEV_dis,t分别为t时刻EV充电和放电的补偿成本;s(t)为EV充电电价;α1、β1分别为微电网对EV充电和放电的补偿系数,分别取0.2和0.5。

g.EV电池损耗成本

将EV电池损耗成本与折旧成本计入EV充放电的损耗成本中,计算方式如下:

CES,t=CEL+CEM

(25)

(26)

式中:CEL、CEM分别为EV放电时损失成本和EV电池折旧成本;KEV为车辆蓄电池的折旧系数;PEVd,j为第j辆车的放电功率。

3.2 约束条件

a.功率平衡约束

微电网功率平衡约束如下:

PWT,t+PPV,t+PDG,t+Pgrid,t=Pload,t+PEV,t

(27)

式中:PWT,t、PPV,t、Pload,t、PEV,t分别为t时段风电出力、光伏出力、常规负荷及EV充放电功率。

b.EV充放电功率及荷电状态约束

EV充放电时功率及荷电状态约束如下:

(28)

λEVcλEVd=0

(29)

SOC,min≤SOC(t)≤SOC,max

(30)

EV充放电状态有3种情况:充电状态(PEVc,t>0,PEVd,t=0);放电状态(PEVc,t=0,PEVd,t>0);闲置状态(PEVc,t=0,PEVd,t=0)。引入状态变量λEVc、λEVd表示EV是否参与充放电(0或1)。

c.联络线功率约束

联络线功率约束表达式如下:

(31)

d.分布式电源出力上、下限约束

各分布式电源出力满足以下条件:

Pi,min≤Pi,t≤Pi,max

(32)

式中:Pi,t为分布式电源i发电功率;Pi,max、Pi,min分别为分布式电源i出力上、下限。

e.DG运行功率约束

DG运行功率约束条件如下:

(33)

式中:Lmin为DG最小负载率。

4 仿真结果分析

4.1 试验数据

仿真算例中PV、WT均运行于最大功率跟踪模式,图5为微电网中风电、光伏出力及负荷需求预测数据。DG的环境补偿成本及排放系数如表1所示,各微电源参数如表2所示,微电网与主网交易电价如表3所示。EV容量为24 kWh,充放电功率均为3 kW,充放电效率μch、μdis均为0.95。本文通过YALMIP建立数学模型,并利用GUROBI求解优化问题。

表1 环境补偿成本及排放系数

表2 微电源参数

表3 微电网与主网交易电价 单位:元/kWh

4.2 结果分析

微电网调度模型求解结果如图6—图9所示。基于各时段风电、光伏功率预测值与平均值,根据式(10)、式(11)计算EV动态充电电价,如图6所示。结合图3、图5可知,在微电网严重缺少电源功率时(17:00—21:00),光伏出力基本为零,风电出力不足以满足负荷需求,微电网中负荷需求基本由DG支撑。此时EV充电负荷将加剧电网调峰负荷,导致系统必须提高DG机组出力满足EV充电和负荷需求,从而使电网运行成本与环境成本增加,因此,此阶段制定EV充电电价较高为1.28元/h。在微电网风电、光伏出力富余时(00:00—07:00、08:00—16:00),负荷水平较低,EV可减少弃风、弃光现象,DG机组只需维持相对较低出力即可满足负荷需求,因此,此阶段EV充电电价制定为0.32元/kWh。

图5 微电网各机组出力曲线

图6 动态充电电价

图7为动态电价引导下的EV充放电功率曲线。结合风电、光伏出力曲线可知,通过充电电价引导,EV作为移动储能装置能够实现对新能源发电的削峰填谷。在微电网严重缺少功率时,EV充电电价维持在1.28元/kWh,激励EV减少充电功率并增加放电功率,从而减少DG机组出力,不仅能缓解调峰负担、EV用户获得更多经济收益,还能减小微电网环境成本。在微电网发电功率富余时,EV充电电价维持在0.32元/kWh,此阶段多余电功率存储到EV。图8为微电网与主网功率交换曲线。在新能源出力或微电网发电功率不足以支撑负荷需求时,通过动态电价引导EV放电或从主网购电满足功率缺额,从而满足微电网内部负荷需求。图9为无序、有序充电弃风弃光曲线,在动态电价引导下EV充电负荷转移到风电、光伏出力较大时段,增加了风电、光伏利用。

图7 动态充电电价引导下EV充放电功率曲线

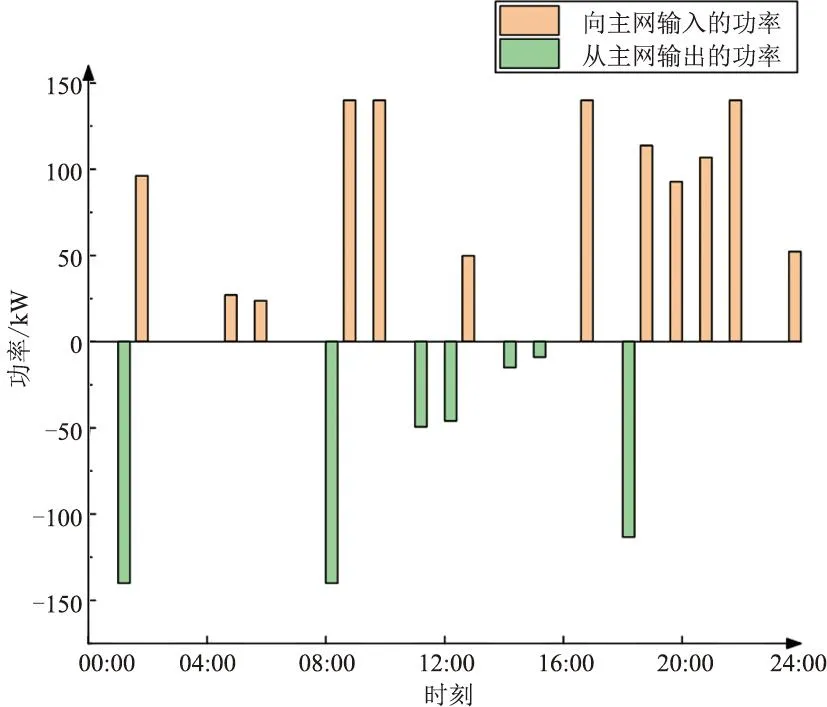
图8 微电网与主网功率交换曲线

图9 无序、有序充电弃风弃光曲线

通过表4成本对比可知,所提方法引导EV在电价尖峰期放电,在电价低谷期充电,不仅降低了EV用户成本,且降低了微电网运行成本及环境成本。微电网总的运行成本降低了16.96%,EV用户成本降低了46.68%,环境成本降低了30.89%。

表4 成本对比 单位:元

5 结语

本文提出了在动态电价机制下考虑EV移动储能的微电网优化调度模型。根据新能源出力大小制定动态充电电价策略,在不影响用户出行的前提下,能引导EV充电负荷最大化消纳风电、光伏,风电、光伏消纳率提高了38.69%,同时通过EV储能减轻了微电网对主网电力需求负担,有利于提高微电网运行的经济性。