风光储氢综合能源系统容量配置策略优化研究

白金彤,董鹤楠,杨雨琪,马少华,宁 晨

(1.沈阳工业大学电气工程学院,辽宁 沈阳 110870;2.国网辽宁省电力有限公司电力科学研究院,辽宁 沈阳 110006;3.朝阳燕山湖发电有限公司,辽宁 朝阳 122004)

0 引言

我国正值技术与经济不断发展且对电力需求日渐增长的阶段,能源枯竭与环境污染等问题也随之加剧。为坚定可持续发展理念,我国提出“双碳”目标正推动着风能、光能等可再生能源的发展,但一些地区大量扩张风光机组,其发电高峰往往与用电高峰相反,导致弃风弃光现象严重,造成了大量能源浪费。

为提高综合能源系统对可再生能源的利用率,将电解水制氢引入系统中[1],并对电制氢单元不断优化,提出了一系列模型与策略。在文献[2]中为降低风电的随机性,在时间上对电解槽精确控制,提出一种基于最小二乘的超短期组合预测模型;文献[3]为更好地结合电制氢与综合能源系统,提出一种碱性电解槽宽功率适应模型,提高了制氢效率;在文献[4]中利用粒子群算法,考虑系统投资、运行及维护保养成本最低和不同购氢渠道情况下的各储能单元容量优化配置;文献[5]提出了一种基于供需平衡的兼顾系统调度灵活性与运行经济性的调度策略;文献[6]以全年制氢最大收益为目标,考虑不同典型日下风光制氢综合能源系统容量配置。上述文献分别对综合能源系统自身性能与经济效益进行优化,但对兼顾稳定性与经济性的研究尚有不足。

本文基于各单元运行特性并考虑各个设备约束条件,构建一种风光储氢综合能源系统数学模型;进而提出一种综合考虑可靠性、经济性及弃电率的多目标容量配置策略;再通过MATLAB软件及商用求解器CPLEX进行系统模型建立及优化求解,结果突出了储氢技术的重要性及不同目标权重对该系统运行结果的影响。

1 风光储氢综合能源系统及模型

1.1 风光储氢综合能源系统组成

本文建立由风电和光伏发电技术为能源供给,并由碱性电解槽制氢,氢气存至储氢罐中配合燃料电池和蓄电池及电负荷构成的独立发电系统,如图1所示。

图1 综合能源系统结构

当风光出力较高或用户负荷较低时,富余电量由蓄电池进行存储并供给电制氢单元进行制氢与储氢;当风光出力较低或用户负荷较高时,蓄电池迅速反应并进行启停动作,平滑电网功率波动[7],同时由储氢系统与燃料电池系统进行发电补足,富余氢气还可进入下游产业,提供经济效益。

1.2 风光储氢综合能源系统建模

a.风力发电模型

根据目前对风力发电技术的研究,可近似得到风力发电功率PW的数学模型[8],如式(1)所示。

(1)

式中:PWN为风机额定功率;vWN为风机额定风速;vin、vout分别为风机的切入、切出风速;ηt为机械传动效率;ηw为电力转换效率;ρa为空气密度;AW为叶轮面积;Cp为风力利用系数;v为实际风速。

b.光伏发电模型

光伏发电输出功率采用符合工程应用的计算方式,如式(2)、式(3)所示。

Ps=ηsAsI

(2)

η(I,Ts)=(a1+a2+a3lnI)·[1-0.005(Ts-25)]

(3)

式中:As为光伏板阵列总面积;I为光伏板接收辐照度总和;ηs为光伏板光电转换效率;Ts为光伏面板运行温度;a1、a2、a3为光伏面板受到的辐照参数。

c.蓄电池模型

蓄电池充放电状态如式(4)、式(5)所示[9]。

(4)

(5)

式中:SOCt和SOCt-1分别为蓄电池在t和t-1时刻的容量;δ为蓄电池内在放电率;PXCH(t)为t时刻蓄电池充电功率;ηXCH为蓄电池充电效率;PXDI(t)为蓄电池t时刻放电功率;ηXDI为蓄电池放电效率;CXCA,max为蓄电池容量允许最大值。

d.碱性电解槽模型

碱性电解槽产氢量和电解槽消耗功率存在函数关系,如式(6)所示[10]。

(6)

式中:VH2为电解槽制氢的体积;ηH2为电解槽制氢效率;PH2为电解槽制氢所耗电量;LH2为氢气低热值;ρH2为氢气密度。

e.高压储氢罐

高压储氢罐的储氢量如式(7)所示[11]。

(7)

式中:SHT,t为t时刻高压储氢罐的储氢量;SHT,t-1为t-1时刻储氢量;qHT,in、qHT,out分别为储氢罐输入、输出的气体量;δHT为储氢罐中储能消耗率;ηHT,in、ηHT,out分别为储氢罐输入、输出的效率。

f.燃料电池

质子交换膜燃料电池氢气能量与功率输出的关系如式(8)、式(9)所示。

(8)

Q=QF,inηC,H2

(9)

式中:VH2为氢气常温下的体积;ηC,H2为储氢罐储氢效率;NA为阿伏伽德罗常数为6.02×1023;VM为气体摩尔体积(常温),约24.5 L/mol;C0为产生的单位库仑电子数量;UFN为额定输出电压;Q为燃料电池能量;QF,in为输入氢气燃料化学能;ηF为燃料电池能量转化效率,取45%。

2 容量优化配置模型

2.1 容量配置目标函数

a.经济性指标

风光储氢综合能源系统年综合成本函数如式(10)—式(12)所示。

C=minf0

(10)

C=CY+(CC+CR+CZ)τ

(11)

(12)

式中:C、CY、CC、CR、CZ分别为系统的全寿命周期总投资等年值成本、初始投资等年值成本、运维成本、残值成本、置换成本;r为实际年利率;n为系统运行年限。

CY取决各单元设备购设成本,如式(13)所示。

CY=nSCS+nWCW+nH2CH2+nFCF+nHTCHT+nXCX

(13)

式中:CS、CW、CH2、CF、CHT、CX分别为光伏、风电、电解槽、燃料电池、储氢罐、蓄电池的单价;nS、nW、nH2、nF、nHT、nX分别为其各模块数量。

系统运维成本CC如式(14)所示。

CFCPF(t)+CHTCPHT(t)+CXCPX(t))

(14)

式中:CSC、CWC、CH2C、CFC、CHTC、CXC分别为各单元单位功率的运维成本;PS(t)、PW(t)、PH2(t)、PF(t)、PHT(t)、PX(t)分别为t时刻其运行功率;T为系统研究年限,本文风光储氢综合能源系统研究年限为20年。

置换成本CZ为风光储氢综合能源系统设备到期后进行更换的费用。其中电解池、蓄电池、燃料电池等设备寿命一般为10年,故需进行更换并计入置换成本,如式(15)所示。

CZ=CH2ZNH2+CFZNF+CXZNX

(15)

式中:CH2Z、CFZ、CXZ分别为电解池、燃料电池、蓄电池的置换成本;NH2、NF、NX为更换次数。

设备残值CR为在系统内设备达到寿命终期后产生残余价值的和,可将初始投资按一定折损比例α计算[12],如式(16)所示。

CR=αCC

(16)

式中:α取值5%。

b.可靠性指标

通过对缺电率(loss of power supply probability,LOPSP)即系统供电能力与负荷需求之间的差距来评估系统可靠性,如式(17)—式(18)所示。

LOPSP=minfL

(17)

(18)

式中:PL(t)为负荷需求功率。

为方便进行经济性分析,将其转换为缺电惩罚费用,统一量纲,如式(19)所示。

CLFa=αLFaLOPSP

(19)

式中:CLFa、αLFa分别为缺电惩罚费用及系数。

c.弃电率指标

系统运行过程中因风光不稳定性与不确定性造成弃风弃光等能源浪费,降低利用率,将这部分损失转换为弃风弃光惩罚费用[13],如式(20)—式(22)所示。

CEFa=minfE

(20)

PESW=PW(t)-PP(t)-PL(t)-PH2(t)-PX(t)

(21)

CEFa=αEFaPESW

(22)

式中:CEFa为弃风弃光惩罚费用;PESW为弃风弃光功率;αEFa为弃风弃光惩罚系数。

本文以风光储氢综合能源系统为研究对象,以系统各单元容量为优化对象,以投资成本、负荷缺电率和弃电率最低为指标,以最小综合费用为目标进行容量配置优化,设置目标函数如式(23)所示。

f=min[ω1f0+ω2fL+ω3fE]

(23)

式中:ω1、ω2、ω3为各指标重要程度权重系数。

2.2 容量配置约束条件

考虑功率平衡约束和各电力单元的运行特性约束保障系统长期稳定运行[14-16],如式(24)—式(29)所示。

a.功率平衡约束为

(24)

b.储能充放电约束与功率约束

电池应避免过充过放,有如下约束:

SOCmin≤SOC≤SOC max

(25)

(26)

式中:SOCmin、SOC max分别为电池允许最小和最大容量值;PDI,min、PDI,max、PCH,min、PCH,max分别为允许最小、最大放充电功率。

c.最大容量约束为

(27)

式中:nW,max、nS,max、nH2,max、nHT,max、nF,max及nX,max分别为风电机组、光伏板阵列、电解池、储氢罐、燃料电池及蓄电池的最大配置数量。

d.电解池功率约束为

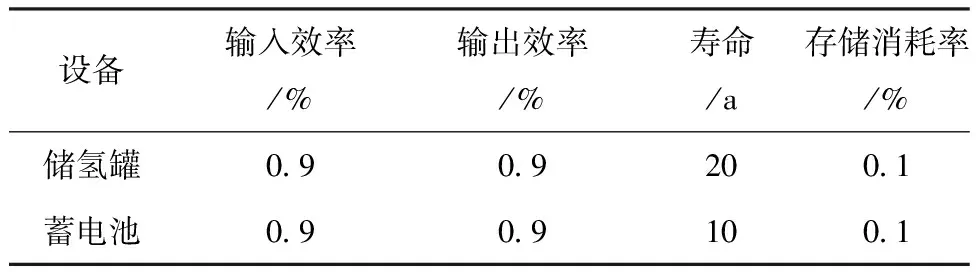
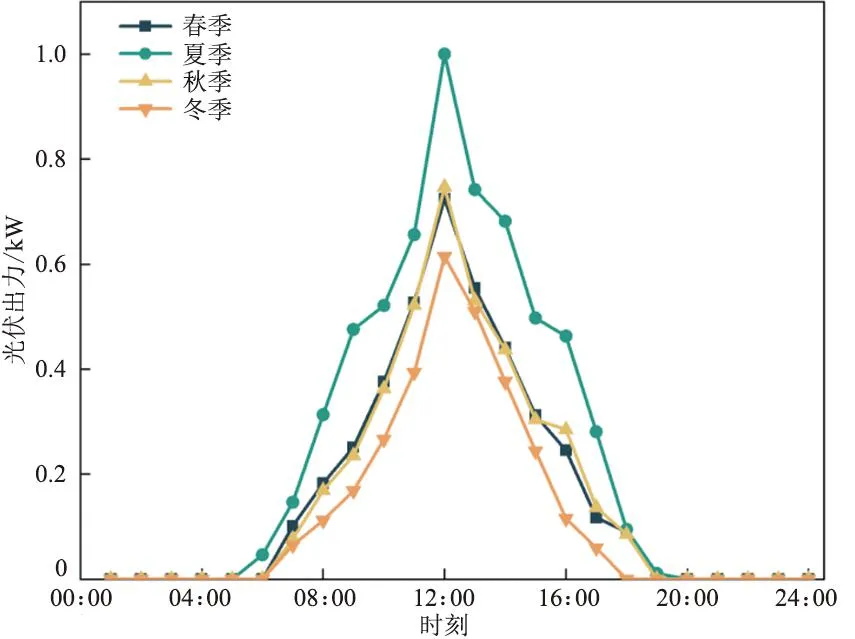
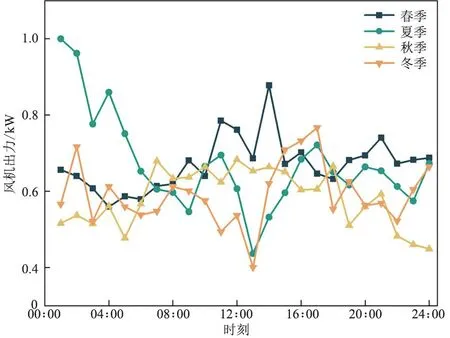
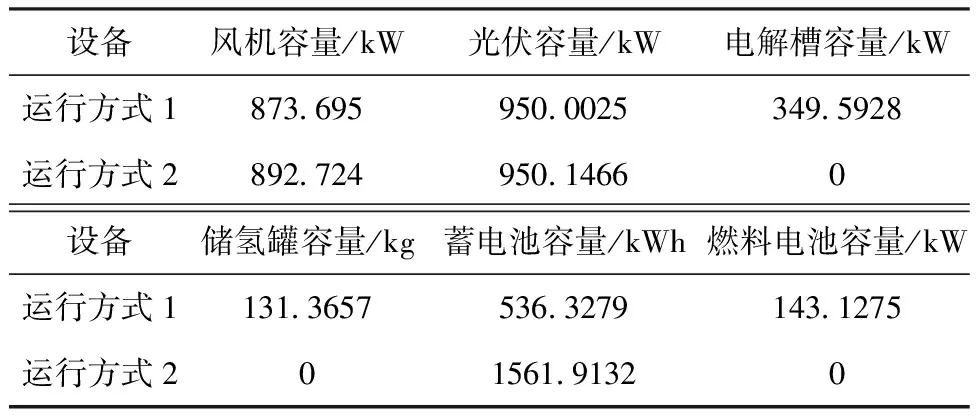
PH2,min

(28)

式中:PH2,max为电解池出力上限,受额定功率限制;PH2,min为电解池出力下限,受最小负载率限制。

e.燃料电池功率约束为

PF,min

(29)

式中:PF,max为燃料电池出力上限,受额定功率限制;PF,min为燃料电池出力下限,受最小负载率限制。

f.储氢罐存储约束

引入等效荷电状态Sohc来研究储氢罐的存储状态,如式(30)、式(31)所示。

Sohc,min

(30)

Sohc=psht/pmax

(31)

式中:Sohc,min、Sohc,max分别为储氢罐容量允许的最小、最大值;psht、pmax分别为储氢罐内的压强和最大压强。

3 算例分析

3.1 基础数据与参数设置

以我国某地区为例,基于四季历史负荷数据及四季中的各1个典型日进行分析,构建时间尺度上的容量分配模型。储能设备技术参数如表1所示,能源转换设备经济参数如表2所示。设定SOC范围为0.1～0.9,Sohc范围为0.2～0.8,风速、光照强度及电负荷之间关系如图2所示。

表1 储能设备技术参数

表2 能源转换设备经济技术参数

由图2可知,负荷是典型双峰曲线,即存在早晚2个用电高峰,冬夏季负荷情况较春秋季需求更大。春秋两季光照时间较长,但光照强度中等,当地总体风力资源丰富且夜间风力明显大于日间。由风光资源结合来看,当地夏季光照强度高且时间较长,但风力较小;冬季光照时间短且强度相对较弱,不过风力总体较夏季强。可见风光资源都存在不确定性与季节性,但在时间分布上存在一定的互补特性。

3.2 优化结果

a.有无储氢技术的系统容量配置

第1种运行方式设为有储氢技术的风光储氢综合能源系统,第2种只含蓄电池作为储能。投资成本、负荷缺电率和弃电率3个指标权重系数设为均权,配置结果如表3所示,参数结果如图3所示。

由表3可知,只通过蓄电池进行储能对蓄电池、风机与光伏板需要较大容量配置,而有储氢技术的系统虽增加了电制氢设备和储氢设备,但减少了几乎2/3的蓄电池用量,这表明有储氢技术的系统能有力分担蓄电池配置。由图3可知,方式1下的目标函数值更低,是未来“双碳”趋势下的更优选择。

(a)负荷曲线

(b)光伏出力标幺值曲线

(c)风机出力标幺值曲线

表3 2种运行方式容量配置结果

图3 2种运行方式下的各参数结果

b.权重系数对容量配置的影响

针对投资成本、负荷缺电率和弃电率3个目标函数,设置3组权重系数,即ω1、ω2、ω3的第1组全为1/3,第2组分别为0.5、0.3、0.2,第3组分别为0.3、0.5、0.2。具体容量配置如表4所示,各参数结果如图4所示。

表4 3组权重系数下的容量配置

由表4和图4可知:①按第2组权重分配即经济性权重较高时,因目前制氢设备成本相对较高,制氢模块和蓄电池的容量配置所需较少,风光机组配置较多,光伏电池较风电机组所需成本较低,故容量配置更大,然而,这种配置方式会导致负荷缺电率和弃风弃光率在3组配置里最高且差距较大,从可靠性的角度来看,系统性能较差,并且存在较多的能量浪费;②当系统缺电率占比较高即按第3组权重分配时,系统配置将优先满足负荷需求,导致发电单元、储能和制氢系统的容量较大,系统可靠性强,制氢系统配置成本较高,经济性较差。

图4 3组权重系数下的各参数结果

可见在多目标容量配置优化中,根据系统所需场景及工程目标改变目标函数权重十分必要。对于本文系统来说,当权重系数相对平衡时,系统综合性能较为优越。

c.负荷增长对容量配置的影响

在上述算例中默认负荷恒定不变,但实际系统运行中负荷会不断增长,参考相关文献,本文设定系统负荷年增长2%,则在运行的第20年将达到最初需求的1.457倍,若此时未进行新的合理容量配置,负荷缺电情况将十分显著,甚至已不足以满足负荷需求。因此,定期调整各个单元的容量配置,以确保综合能源系统在其寿命周期内向用户提供可靠的电能供应。由表1可知,蓄电池、燃料电池和电解槽在第10年结束时达到寿命终期,需进行设备更换,同时可进行系统各单元容量配置调整,满足用户侧负荷需求,且第20年时缺电率低于10%,容量配置更新后如表5所示。

表5 含负荷增长的容量配置结果

4 结语

本文建立了风光储氢综合能源系统,并考虑全寿命周期负荷增长,提出一种满足各设备约束条件以投资成本、负荷缺电率和弃电率为优化目标的多目标容量配置优化方法。通过MATLAB及商用求解器CPLEX进行优化分析,对比有无储氢技术参与的2种运行方式及考虑目标函数不同权重对容量配置的影响,分析得出有储氢技术即风光储氢综合能源系统运行方式且3种优化目标等权重下的容量配置系统可靠性较好。该方法可为研究风光储氢综合能源系统容量配置优化提供参考。