区域双碳目标与预测研究

刘东格,孟繁华,冯 瑞,衣丽葵

(沈阳工程学院电力学院,辽宁 沈阳 110136)

0 引言

随着全球变暖和温室气体排放的增加,各国纷纷意识到减少碳排放的重要性,并开始制定碳减排目标。区域双碳目标是指在国家或地区范围内制定的碳减排目标,旨在应对气候变化和实现可持续发展[1]。

许多国家和国际组织已开始研究区域双碳目标与路径规划[2]、气候科学、能源经济学、环境科学等多个领域[3],主要集中在制定双碳目标的原则、碳减排政策等理论,并未给出系统的评估方法[4]。本文在区域双碳目标与路径规划研究基础上,进一步探讨德尔菲法[5]、差异性分析法[6-7]和多元线性回归模型[8]在此领域的应用。研究范围包括指标体系的确立、与碳减排目标相关的因素分析、路径规划的决策支持和政策评估等[9]。

为了选取合适的理论和技术方案,参考相关研究成果和理论框架,并结合具体的研究对象和目标进行选取。德尔菲法作为一种专家咨询方法,可用于获取专家意见和建立共识;差异性分析法可帮助比较不同方案的优缺点;多元线性回归模型可提供经验分析和预测能力[10]。这些方法的选取基于在区域双碳目标与路径规划研究中的适用性和有效性。通过对多种分析方法的运用,为决策者提供科学、准确的数据和方法支持,以制定可行的路径规划方案。

1 评估指标体系的构建

1.1 筛选方法

通过文献研究,结合建立社会稳定风险评价的特殊性和繁杂性,本文主要运用专家问卷法进行风险评价的指标体系构建,对该方法的应用原理和适用性进行说明。德尔菲法是指调查人员按照规定的流程对专家发放调查问卷,在专家对调查人员提出的问题回答完毕后,统一对数据归纳整理,并再次向专家征询意见,进一步整理数据,最终产生结果。这种方法可有效减少主观因素造成的影响[5]。

德尔菲法选取指标的主要步骤如图1所示。

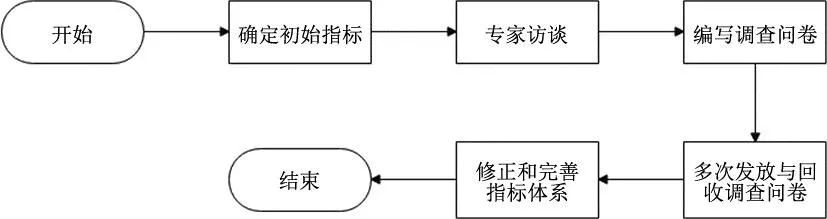
图1 德尔菲法流程

1.2 指标体系确定

根据三轮征询,并不断修订与完善,最终确定人口、生产总值、能源消费量、产业能耗结构、能耗品种结构、碳排放量、能源消费部门碳排放因子、外地调入电力碳排放因子为区域碳排放量及经济、人口、能源消费量评价指标体系。

2 区域碳排放量分析及其影响因素

2.1 碳排放量状况

对某区域数据进行汇总,得出2011年—2020年期间的碳排放量状况,如图2所示。

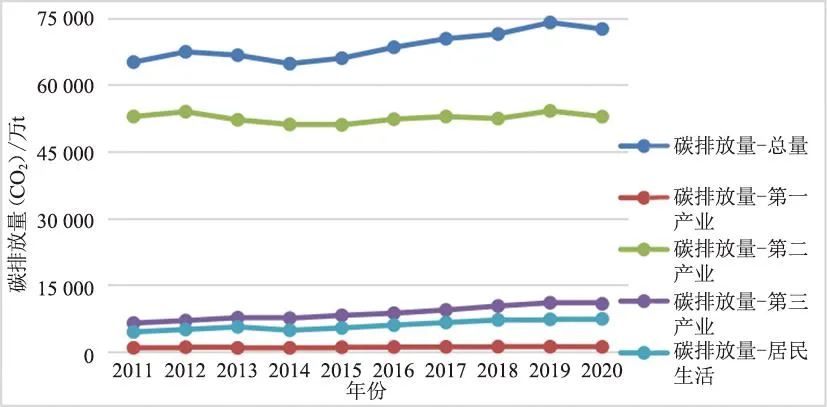
图2 某区域碳排放量状况

在十二五期间(2011年—2015年),总体上碳排放量呈增长趋势。在十三五期间(2016年—2020年),碳排放量继续增长,但在2020年稍有下降;第三产业和居民生活的碳排放量在10年中呈上升趋势。

2.2 碳排放总量对比

计算2011年—2015年和2016年—2020年2个时期的总碳排放量,如图3所示。

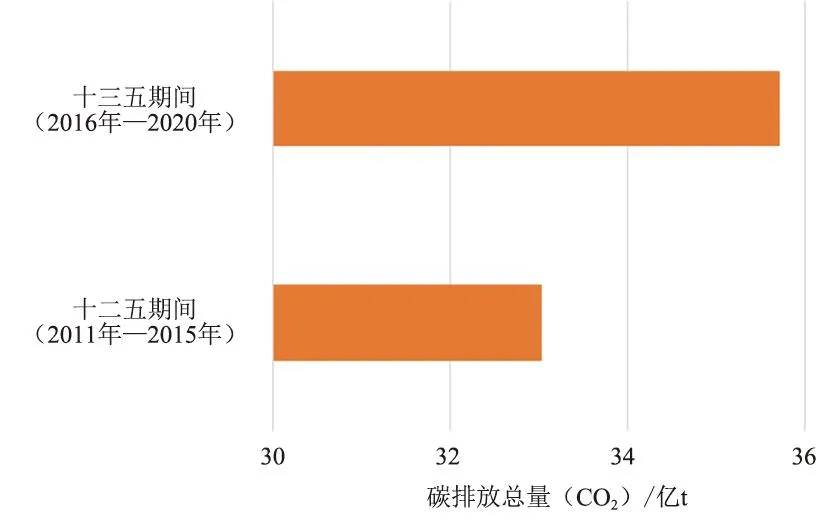
图3 十二五与十三五碳排放总量对比

由图3可知,在十三五期间的碳排放总量比十二五期间增加约26 835.92万tCO2,说明在这2个五年计划期间,碳排放总量仍在增加。

3 差异性分析

差异性分析是一种用于比较不同组别之间差异的统计方法,主要目的是确定组与组之间的差异是否显著,进而推断这些差异是否由随机因素引起。常用于比较2个或多个组的均值、比例或其他统计指标。在差异性分析中,常用方法包括方差分析(ANOVA)、T检验、卡方检验、回归分析等。这些方法可以帮助研究者评估组别间的差异是否显著,并提供统计支持[11-18]。

差异性分析步骤如图4所示。

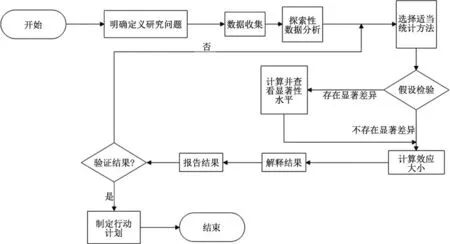
图4 差异性分析流程

3.1 正态性检验

根据上述数据可得其正态性检验结果如表1所示。

表1 正态性检验 单位:万tCO2

结果分析均采用S-W检验:

a.碳排放量总量的显著性P值为0.495,水平上不呈现显著性,不能拒绝原假设,因此数据满足正态分布;

b.第一产业-农林消费部门,显著性P值为0.123,水平上不呈现显著性,不能拒绝原假设,因此数据满足正态分布;

c.第二产业-工业消费部门,显著性P值为0.481,水平上不呈现显著性,不能拒绝原假设,因此数据满足正态分布;

d.第三产业-总量,显著性P值为0.557,水平上不呈现显著性,不能拒绝原假设,因此数据满足正态分布;

e.居民生活-居民生活消费,显著性P值为0.367,水平上不呈现显著性,不能拒绝原假设,因此数据满足正态分布。

利用观测数据判断总体是否服从正态分布的检验称为正态性检验,是统计判决中重要又特殊的拟合优度假设检验。

根据数据正态性检验的结果,若正态图基本呈现钟形(中间高,两端低),说明数据虽然不是绝对正态,但基本为正态分布。碳排放量-总量、第一产业-农林消费部门、第二产业-工业消费部门、第三产业-总量、居民生活-居民生活消费的正态性检验结果如图5所示。

(a)碳排放量-总量

img id="7f6f3cdee3edfc07a7969a5a22468134" class="picture_figure" src="images/71201ed80d5d37c3018a2d0a5bbe0c98.jpg" width="213" height="102" title="width=213,height=102,dpi=110" />

(e)居民生活-居民生活消费

图5 正太性检验结果

Q-Q图的全称是“Quantile-Quantile Plot”,在 MATLAB中,使用qqplot函数生成Q-Q图,通过直观观察Q-Q图的形状来评估数据是否符合正态分布。在Q-Q图中,如果图中的点大致沿着一条直线分布,且曲线形状近似于钟形,那么数据更可能近似正态分布。

3.2 方差齐性检验

根据上述数据可得其正态性检验结果,如表2所示。

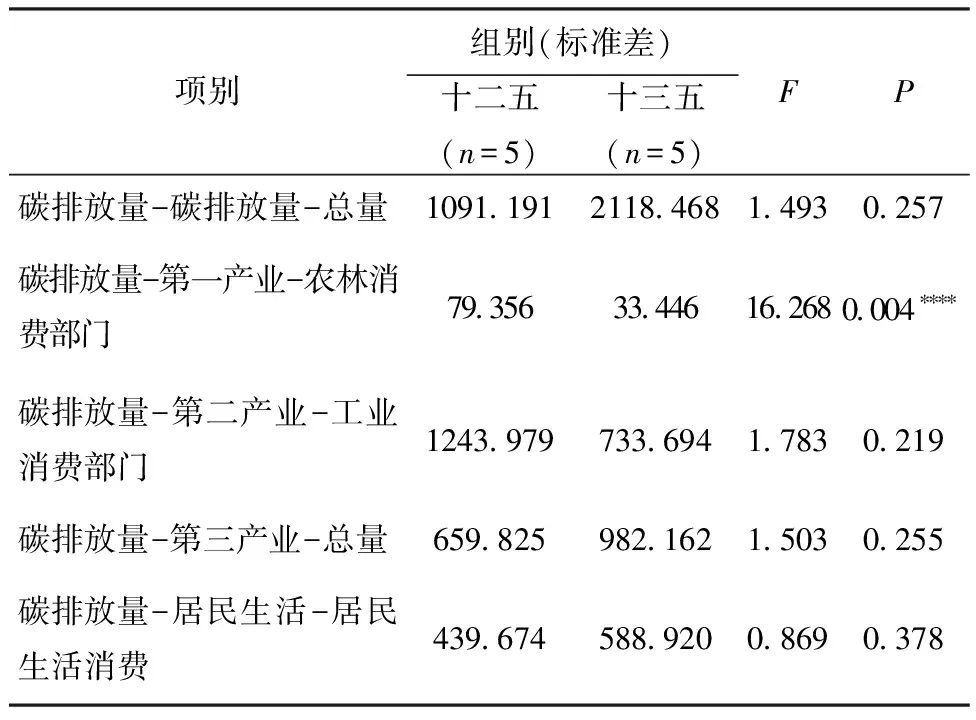
表2 方差齐性检验 单位:万tCO2

方差齐性检验的结果显示:对于碳排放量-第二产业-工业消费部门,显著性P值为0.219;对于碳排放量-第三产业-总量,显著性P值为0.255;对于碳排放量-居民生活-居民生活消费,显著性P值为0.378,水平上均不呈现显著性,均不能拒绝原假设,因此数据均满足方差齐性。

3.3 独立样本T检验分析结果

根据上述结论及其数据可得其独立样本T检验分析结果,如表3所示。

表2和表3中,“***”、“**”、“*”分别代表1%、5%、10%的显著性水平;0.20,0.50和0.80分别对应小、中、大临界点。

根据表3可知,十二五、十三五在碳排放量-碳排放量-总量的均值分别为66 074.683/71 441.868;由于满足方差齐性,采用独立样本T检验,显著性结果P值为0.001***,因此统计结果显著,说明十二五、十三五在碳排放量-碳排放量-总量存在显著差异;其差异幅度Cohen’sd值为3.185,差异幅度非常大。

表3 独立样本T检验分析 单位:万tCO2

十二五、十三五在碳排放量-第一产业-农林消费部门的均值分别为1077.459/1253.737;由于不满足方差齐性,采用Welch’s T检验,显著性结果P值为0.005***,统计结果显著,说明十二五和十三五在碳排放量-第一产业-农林消费部门存在显著差异;其差异幅度Cohen’sd值为2.895,差异幅度非常大。

十二五、十三五在碳排放量-第二产业-工业消费部门上的均值分别为52 308.601/53 010.888;由于满足方差齐性,采用独立样本T检验,显著性结果P值为0.309,因此统计结果不显著,说明十二五和十三五在碳排放量-第二产业-工业消费部门不存在显著差异;其差异幅度Cohen’sd值为0.688,差异幅度中等。

十二五、十三五在碳排放量-第三产业-总量的均值分别为7502.882/10 160.826;由于满足方差齐性,采用独立样本T检验,显著性结果P值为0.001***,因此统计结果显著,说明十二五和十三五在碳排放量-第三产业-总量存在显著差异;其差异幅度Cohen’sd值为3.177,差异幅度非常大。

十二五、十三五在碳排放量-居民生活-居民生活消费的均值分别为5185.741/7016.417;由于满足方差齐性,采用独立样本T检验,显著性结果P值为0.001***,因此统计结果显著,说明十二五和十三五在碳排放量-居民生活-居民生活消费存在显著差异;其差异幅度Cohen’sd值为3.523,差异幅度非常大。

4 区域碳排放量及其关联模型

4.1 相关指标变化

同比是今年某个阶段与去年相同时段相比,适用于观察某个指标在不同年度的变化;环比是某个阶段与其上一个时长相等的阶段作比较。其计算方法为

环比增长率=(本期数-上期数)/上期数×100%

(1)

同比增长率=(本期数-同期数)/同期数×100%

(2)

通过同比和环比分析,可了解数据的增长趋势。同比可知年度趋势,而环比则有助于观察季度或月度内的波动。这2种方法都有助于制定经营策略和预测未来趋势。

根据已知数据可得同比和环比对比图,如图6、图7所示。

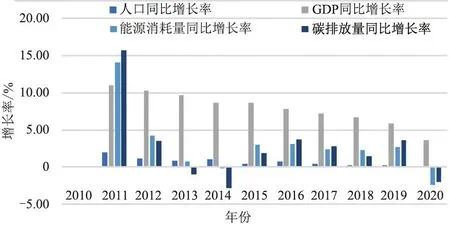
图6 同比增长对比

由图6、图7可知,在2010年—2020年期间,中国人口同比增长约7.72%;GDP同比增长约114.17%;能源消耗量同比增长约33.57%;碳排放量同比增长约28.87%;然而在2019年—2020年,能源消耗量和碳排放量均出现下降,分别下降约2.45%和1.97%,可能与能源效率的改善和环保政策的实施有关。

图7 环比增长对比

4.2 多元线性回归模型

多元线性回归模型是一种用于建立和分析多个自变量与一个因变量之间关系的统计模型,是线性回归分析的扩展,可以同时考虑多个自变量对因变量的影响。

在多元线性回归模型中,假设因变量与自变量之间存在线性关系。模型的目标是通过最小化观测值与模型预测值之间的差异来估计自变量系数,并建立一个能够解释因变量变异的模型[8]。

根据上述数据,可建立人口、生产总值、能源消费量、产业能耗结构、能耗品种结构、碳排放量、能源消费部门碳排放因子、外地调入电力碳排放因子和碳排放量之间的关联关系模型。其关系可用多元线性回归模型来表示,其中人口、生产总值、能源消费量、产业能耗结构、能耗品种结构、碳排放量、能源消费部门碳排放因子、外地调入电力碳排放因子作为自变量,分别表示为X1～X8,碳排放量作为因变量。本文的时间跨度为2010年—2020年。

碳排放量=α+β1X1+β2X2+…+β8X8+ε

(3)

式中:α为截距项,表示当所有自变量为零时的碳排放量;β1-β8为回归系数,表示各自自变量对碳排放量的影响;ε为去除自变量X1-X8对因变量碳排放量产生的随机误差。

模型的核心假设自变量与某区域碳排放量之间的关系可用线性方程来表示,说明自变量的变化可反应某区域碳排放量的变化。

根据已知数据结合MATLAB进行多元线性回归分析模型处理可得表4。

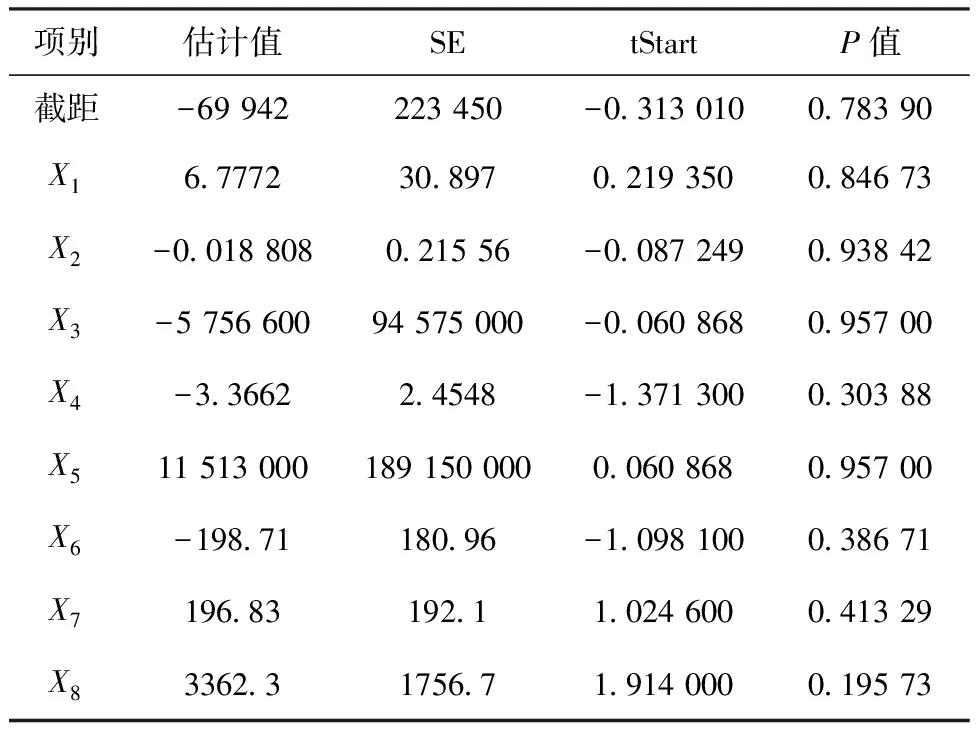
表4 多元线性分析参数

通过分析这些模型参数,可以了解因变量随着每个自变量的演变趋势。表4中SE(standard error)为标准误差;tStart(t-statistic)为用于检验一个参数估计值与零假设之间的差异是否显著的统计量,无论tStart 统计量的值是正还是负,其绝对值越大,表示对应的回归系数的显著性越高。以人口(X1)为例,估计系数为 6.7772,X1的tStart为正,P值为0.846 73(如果P值小于显著性水平0.05,则估计系数被认为是显著的),说明人口对碳排放量的估计系数不显著。即在这个模型下,人口对碳排放量的影响不显著。

4.3 碳排放预测模型

结合上述数据运用MATLAB对未来10年的碳排放量进行预测,观测次数为11次,误差自由度为2,均方根误差为809,R2=0.999,调整后的R2=0.993,F统计量与常数模型为179,P=0.005 58,预测结果如图8所示。

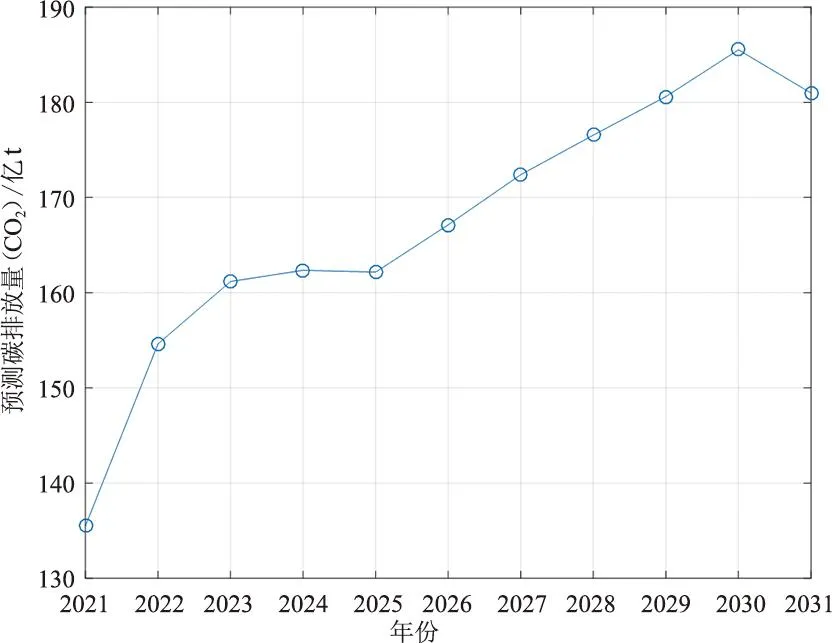
图8 未来10年碳排放量预测

预测结果可知R2接近1,F统计量和P值表明模型的整体性能非常好,说明模型可以很好地用于预测数据。

5 结论

本文讨论了指标体系的评估问题,利用历史的样本数据,建立差异性分析及多元线性回归分析模型,对回归系数进行预测,验证了模型拟合、预测结果的可行性和有效性。本文所提方法还有很大的理论探讨空间,制定双碳路径规划需考虑差异化。

a.产业结构调整。重点减少工业部门的碳排放,鼓励高效低碳生产方式,推动产业升级和转型。

b.能源转型。大力发展可再生能源,减少对化石燃料的依赖,提高能源效率,同时推动电动交通等低碳交通方式。

c.碳定价机制。引入碳定价机制,通过碳市场激励企业减少碳排放,鼓励碳交易和碳汇市场发展。

d.居民生活。通过教育和政策措施,鼓励居民采用更环保的生活方式,包括节能碳减排、绿色出行和垃圾分类等。

双碳路径规划应该综合性考虑,需要在政府、企业和居民之间形成共识,确保可持续发展的同时减少碳排放。