基于分时电价的多目标电动汽车有序充电优化策略研究

李媛媛,侯锦秋,宋 阳,刘艳梅

(1.沈阳工程学院电力学院,辽宁 沈阳 110136;2.国网辽宁省电力有限公司物资分公司,辽宁 沈阳 110006)

0 引言

传统的以化石能源作为基础的能源消费结构,对生态环境造成了不可逆转的影响[1]。为了减少对环境的破坏、缓解能源紧张,达到能源的可持续发展,以电力为能源的新能源汽车越来越普及。然而,越来越多的新能源汽车的无序并网会给配网负荷的平稳运行带来较大的冲击[2]。因此研究新能源汽车的有序充电策略具有重要意义。

文献[3]根据每台汽车接入电网时的负荷信息动态更新峰谷电价,以充电量最多和充电成本最小为目标函数,采用粒子群算法对其优化,并修正其优化后的状态,得到的优化控制策略可以降低用户的充电成本。文献[4]综合考虑了机组的运行成本及弃光弃风电动汽车的充放电成本,以最小化调度周期内的成本为目标,采用改进蜂群算法求解,得到了成本最小的优化调度模型。文献[5]在粒子群算法基础上结合遗传算法,求解其建立的波动率最小及用户花费最小的目标函数,得到优化结果。文献[6]分2阶段对多目标充电策略求解,先进行削峰填谷,再对高峰负荷进行进一步优化。文献[7]将电动汽车(electric vehicle,EV)的优化调度问题分解为多个子问题,建立充电站收益最大化的优化策略。文献[8-9]构建了双层优化模型进行充电策略的优化,保证电网负荷平稳的同时,降低了用户的充电费用。文献[10]采用聚类算法对EV进行优化调度,使用户顺利完成充电且保证了电网运行的平稳。文献[11]针对大量电动汽车接入电网后的无序充放电对电网造成的不利影响,提出了一种基于实时电价的双层优化调度模型。

综上,本文考虑用户对于分时电价的响应,以电网的负荷波动率最小及用户充电费用最小为目标,建立多目标优化模型,同时动态调整2个目标的动态权重系数,采用改进后的粒子群算法进行寻优。电动汽车的充放电调度问题存在着维度高、变量多、非线性等问题,传统的粒子群算法容易陷入局部最优,难以得到最优解。本文对其进行简化,并加入了瑞利飞行寻其粒子最优,扩大了粒子搜索范围。最后通过仿真分析验证了方法的有效性。

1 电动汽车建模

1.1 电动汽车出行建模

EV用户每日的出行时刻,每天所行驶的里程数以及结束行程的时刻都决定了EV的负荷模型。电动汽车每日出行时刻的概率密度函数[12]为

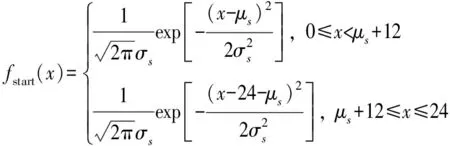
(1)

式中:μs为用户每日离开的最早时间期望值,取8.92;σs为用户每日最早离开时间的标准差,取3.24。

电动汽车每日结束行程时刻的概率密度函数为

(2)

式中:μb为用户每日结束行程的时间期望值,取17.47;σb为用户每日结束行程的时间标准差,取3.41。

电动汽车的日行驶里程概率密度函数为

(3)

式中:σD为用户每日行程的标准差,取1.14;μD为用户每日行程的期望值,取2.98;d为每日的行驶里程,km。

1.2 电动汽车无序充电建模

考虑到EV车主的用车习惯及EV的充电时间、行驶里程、电池容量、充电环境、充电效率等因素,得到充电模型,对于第i台并网的EV有:

(4)

用户可自行选择充电时间,在无充电优化的前提下,电动汽车并网则开始进行充电,将1天中每15 min定为1个时间段,则将1天分为96个时间点,则时段t的充电负荷为

(5)

式中:Ln为每个时间段内EV总充电负荷;N为EV的数量;PEVi为第i台EV的充电功率。

2 考虑分时电价的电动汽车充电模型

在电力系统中通常采用分时电价来进行削峰填谷,用户对于不同的电价有较大的响应。当峰谷电价相差明显时,用户对其的响应更加明显。随着V2G(vehicle to grid)技术的发展,电动汽车被看作移动的分布式电源[13],如果电动汽车用户的充电行为受分时电价的充分影响,对于电网的削峰填谷效果将更好。当固定了分时电价之后,负荷会随着电价的变化而发生改变,当峰谷电价相差更大的时候,用户对于价格将更加敏感,负荷对于电价的改变更加明显,当峰谷电价相差较小时,用户对其将不再敏感,则失去了分时电价的意义[14-15]。考虑到充电汽车充电时长受剩余电量的影响,且充电周期涉及多个充电周期,则引入弹性因子elj。

(6)

式中:ql为l时刻的电量;gj为j时刻的电价。

全天24小时分为m个时刻,电量与电价之间具体的关系如下:

(7)

(8)

式中:E为电价电量弹性矩阵。

引入分时电价之后,则:

(9)

(10)

式中:kl为各个时期收费利率的变化情况;rl为电价指导实施后不同间断时刻的负荷变化情况,将式(10)代入式(6)、式(7)可得峰谷平各个时刻的电价负荷变化率。

本文采用的峰谷电价标准见表1,将采用3个时段,将1天划分为峰谷平3个收费标准[16]:

表1 北京市峰谷平电价政策 单位:元/kWh

2.1 目标函数

在电动汽车充电进行负荷优化的过程中,对负荷有削峰填谷的效果,同时会减小负荷的波动率。削峰填谷的效果越明显,负荷的波动率越小,负荷波动率小会提高电能质量[17]。为使电动汽车并网后对电网的冲击最小,尽可能削峰填谷,本文在电网侧建立负荷波动率最小的目标函数。

(11)

式中:通过负荷标准差与均值的比值反映负荷的波动率。将1天之内分为Tn个优化时段,单位优化时长则为1440/Tn,则:

(12)

Pt=PBt+PEVt

(13)

(14)

式中:Pt为该时段总负荷;PBt为对应时段基础负荷。

同时,以用户视角来看,充电费用最小是其追求的目标,本文以用户充电费用最小为另一目标函数:

(15)

综上所述,式(15)为本文的目标函数,现将多目标函数其赋予不同的目标权重,得到了整体的目标函数。

minF=ω1F1+ω2F2

(16)

式中:供电侧与用户同样重要,故取相同的权重,ω1=0.5,ω2=0.5且ω1+ω2=1。

2.2 约束条件

a.EV的充电数量约束

n≤N

(17)

式中:n为当前小区内的充电电动车数;N为小区内总的电动车数。

b.EV的充电电量约束

1)EV结束充电时,车主预期的充电量与实际充电电量之间的关系:

SOC exn≤SOC endn≤1

(18)

式中:SOC exn为第n台EV的预期充电电量;SOC endn为第n台EV结束充电时的电量。

2)充电量与电池状态的关系约束:

(19)

式中:SOC stn为第n台EV充电之前的充电状态;Qn为第n台EV的充电功率;Tendn为第n台EV结束充电的时间;Tstn为第n台EV开始充电的时间;Cn为第n台EV的电池容量。

c.为了保证车主的经济利益,新的充电费用应该低于实施前的费用。

F0=q0·g0

(20)

(21)

ql=∑qln

(22)

式中:F0为无序充电时的费用;F1有序充电时的费用;q0和g0分别为EV无序与有序时总负荷与原电网的固定电价。

3 改进粒子群算法

粒子的速度处于发散状态会对算法的收敛性有较大的影响。本文舍弃其速度项,完全凭借粒子的位置对其进行控制,得到式(23)。同时为了防止陷入局部最优,引入瑞利飞行重新调整粒子位置。瑞利飞行是一种服从正态分布的搜索路径,有效防止陷入局部最优。粒子的更新方式为式(24)。

(23)

(24)

采用Mantegna算法模拟瑞利飞行的步长,步长的公式为

(25)

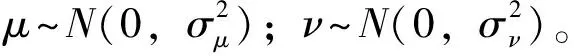
(26)

σν=1

(27)

式中:β通常取1.5。

算法的具体流程如图1所示。

图1 改进粒子群算法流程

4 算例分析

4.1 数据及参数设置

本文以某园区居民的基本用电负荷为基础,园区内有500台EV,对用户进行用车模拟,得到无优化的充电负荷模型。电池容量为40 kWh,按照电动汽车基础设施统计数据设置快充充电功率PF=54 kW,占比20%;慢充充电功率PL=7 kW,占比80%。均衡考虑供电与用户的需求,多目标优化权重w1=w2=0.5。

4.2 运行结果

该小区500台EV没有优化的负荷功率曲线与居民原来用电负荷功率叠加得到的结果见图2。由图2可知,在20时左右用电高峰期,负荷功率的峰值过高,负荷波动率过大,对电网的稳定性造成影响。同时,在这个时间段的电价也处于高峰,用户的充电费用也过高。

图2 无序充电下的负荷曲线

本文设置谷时段电价为0.36元/kWh,平时段电价为0.86元/kWh,峰时电价为1.38元/kWh,具体时段如图3所示。

图3 不同时间段的电价

图4对比了本文方法、传统的粒子群算法以及遗传算法,对所提出的目标函数进行求解,优化指标见表2,由结果可知,在无序充电的情况下,遗传算法、传统粒子群算法以及本文算法的条件下,负荷的峰谷差分别为2588.02 kW、2277.21 kW、2270.64 kW、1707.11 kW,负荷波动率分别为56.38%、54.68%、54.37%、52.06%,充电费用为8746.25元、8574.98元、8490.69元、8211.07元。由仿真结果可知,采用本文的方法优化结果最优,验证了本文方法的有效性。

图4 不同优化方法下的负荷曲线

表2 不同优化方法下的电网负荷评价指标

5 结语

对于目前电动汽车行业的迅猛发展,研究电动汽车的有序充电策略至关重要。本文以分时电价为基础,建立了负荷波动最小以及用户经济效益最好的目标函数,采用改进的粒子群算法进行求解。通过仿真分析,对比其他方法得到的负荷波动率以及用户充电费用,验证了该方法的优越性。在今后的研究中可以将电价设置与负荷实时变化相结合,进一步有针对性研究优化电动汽车的充电策略。