周期性多层排桩低频隔振及衰减域拓宽研究
高赟杰 姚文山 王子立 李泰灃 王业顺
1.中建交通建设集团有限公司, 北京 100071; 2.中国铁道科学研究院集团有限公司 铁道建筑研究所, 北京 100081;3.中南大学 土木工程学院, 长沙 410083
轨道交通在给人民带来便利的同时,引起的环境振动问题也日趋严重,尤其是10 Hz以下的低频轨道交通振动,因传播距离长、衰减慢,危害性更大[1-2]。在众多隔振手段中,周期性排桩作为非连续隔振屏障因施工方便、成本较低、适应性强,具有较好的应用前景[3],如图1所示。
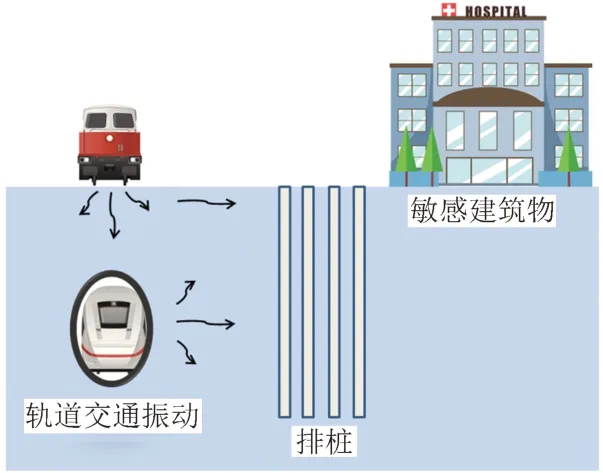
图1 周期性排桩隔振
针对周期性排桩隔振问题,国内外学者开展了大量研究。在数值研究方面,文献[4]通过数值研究,发现扩大桩基直径可以拓宽带隙频率。文献[5]模拟了不同填充材料下周期性填充排桩隔振效果,研究发现填充软体材料时排桩隔振效果更好,且扩大桩径可以获得20 Hz以内的低频带隙。文献[6-7]提出了一种周期排桩隔振时表面波识别新方法,并研究了周期排桩在层状土中表面波隔振性能。文献[8]提出可用COMSOL PDE模块计算周期排桩的频域和时域。为获取更低频率带隙,文献[9]研究发现在饱和土中,周期性管桩可获得15~20 Hz低频衰减域。文献[10]通过数值模拟,研究了周期排桩对低频瑞利波的隔振性,探索了不同桩截面的隔振效率,发现十字形截面隔振效果最好,并可以产生9.64 ~ 13.92 Hz的低频带隙。文献[11]提出了大型尺寸隔振桩基,当桩基直径为8 m,排间距为10 m时可获得10 Hz以下的带隙。在试验方面,文献[12]开展周期性PVC管桩表面波隔振室内试验,并将试验结果与数值模拟复频散计算结果对比,验证了周期排桩隔振性能。文献[13]开展原理性试验,研究周期性空心桩和填土桩隔振性,发现实测振动衰减达50% ~ 98%,其中水平衰减优于竖向衰减,且填土桩对振动波衰减作用更好。文献[14]通过现场试验,研究了周期性空心孔的隔振性能,研究结果与数值模拟一致,验证了周期性超材料在土壤材料中的适用性。为获得更低的隔振带隙,基于局域共振机理设计桩基形式,文献[15]提出了一种多层桩基结构,通过复频散研究发现,该桩基可以获得低频隔振带隙。进一步,文献[16]研究了多层桩中管桩对隔振性能的影响,发现管桩可以增大桩-土弹性模量,提升隔振性能。
已有研究肯定了周期排桩的隔振性能,也提出了多种低频隔振结构,然而,只关注低频带隙,极少关注低频带隙宽度。通常带隙频率越低,带隙宽度越窄。由于实际环境振动主频是一个范围,而非某一固定值,极窄的带隙很难覆盖全部振动主频,不利于实际隔振应用。因此,本文基于局域共振机理,首先在多层桩中引入一种截面带孔软体层,通过减小软体层填充率来获取更低频带隙;其次,针对不同低频带隙的多层桩,创新性提出“中心频段连续”的排桩组合隔振方式,并通过频域和时域模型深入分析其隔振机理。
1 周期结构隔振
1.1 基本理论
假设土体为弹性体,在不考虑体积力影响下,弹性单元振动形式可以表示为[17]
式中:∇为哈密顿算子;r为位置矢量,r= (x,y,z);u为位移矢量,u =(ux,uy,uz)T;ρ(r)为材料密度;λ(r)和μ(r)为拉梅常数。
以平面波为例,单元体位移[u(r,t)]为
式中:ω为圆频率;U(r)为振幅。
把式(2)代入式(1)中,化简得到
在周期结构中,根据bloch理论,有
式中:uk(r)为调幅函数;k为波矢。
在周期矢量为R的周期结构中,调幅函数为周期函数,即
将式(5)代入式(4)中,可得周期性结构中单胞边界条件,即
将式(6)代入式(3),可得到关于k,ω和uk(r)的方程组,进一步可获得ω与k的特征方程。
以多层桩正方形排布为例,如图2所示,晶格常数为a,不可约布里渊区是三角形区域ΓΧМ。只需将波矢(k)扫掠不可约布里渊区边界,即可获得ω与k之间的频散曲线。本文利用COMSOL Multiphysics有限元软件求解特征方程,并求得ω与k之间的频散曲线。
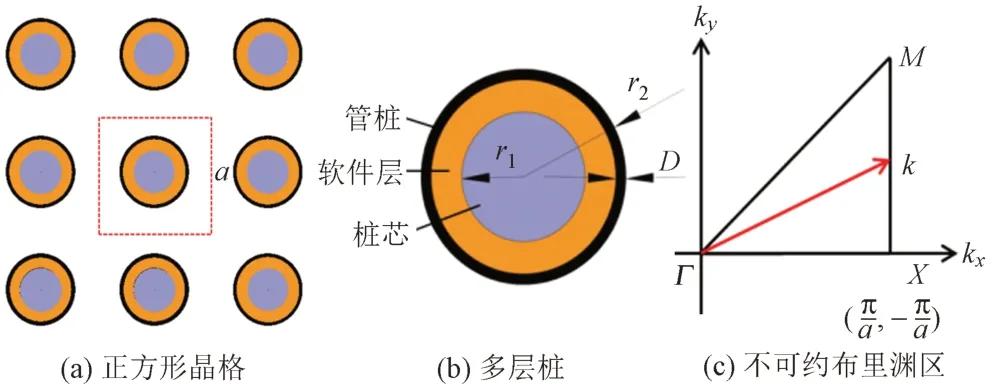
图2 多层桩正方形排布
1.2 典型频散曲线
当晶格常数a= 2 m,管桩外径r2= 0.76 m,管桩厚度D= 0.02 m,桩芯半径r1= 0.65 m时,材料力学参数取自文献[11],见表1,计算频散曲线如图3所示。在11.086 ~ 14.910 Hz内形成了一条完全带隙,意味着这个区间内的弹性波将被周期结构隔断。带隙下边界出现了较长的平直带,表明带隙机理为局域共振机理,该机理也是获得低频表面波带隙的重要途径。

表1 材料参数
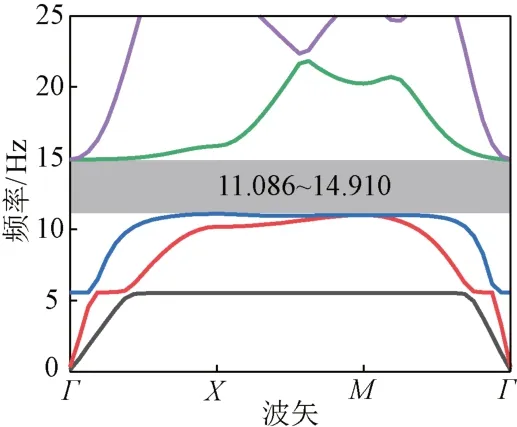
图3 频散曲线
1.3 研究内容及方案
局域共振带隙频率虽然较低,但其带隙宽度也较窄,从而限制了局域共振结构隔振的实用性。本文主要针对周期性多层桩局域共振带隙,通过优化软体层结构及排桩组合形式,来获取低频宽衰减域。
降低软体层填充率可以获取更低频率共振带隙[18]。如图4所示,本文提出一种截面带孔型软体层结构,保持圆孔半径恒定,通过控制圆孔数量来调节软体层填充率。
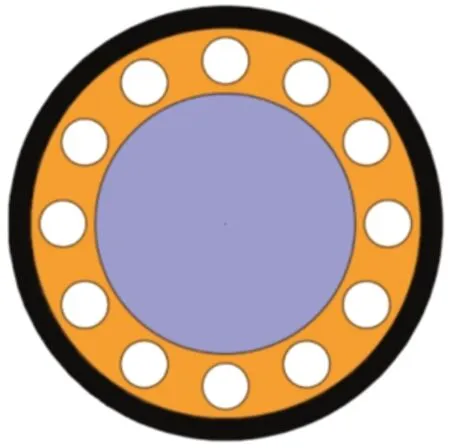
图4 截面带孔型软体层
本文包括三项研究内容:①研究软体层填充率对周期性多层填充桩带隙的影响。对截面带孔型软体层展开研究,计算软体层填充率(W)为35% ~ 100%时周期性多层填充桩的频散曲线,分析软体层填充率与带隙的关系。②开展频域分析,研究有限数量排桩组合隔振特征,探索低频宽带的排桩组合方法。③通过时域分析,深入研究组合排桩隔振机理。研究技术路线如图5所示。
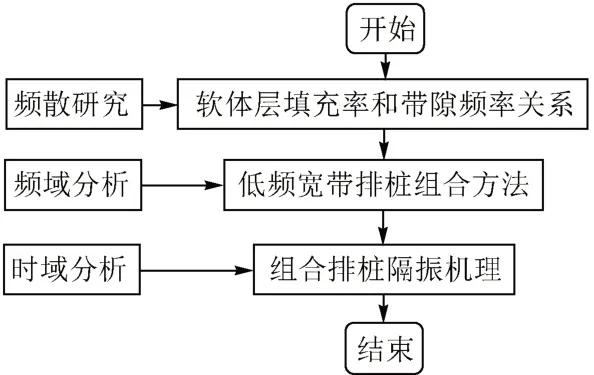
图5 技术路线
2 软体层填充率对带隙的影响
轨道交通振动主要有高频(100~400 Hz)、中频(30~60 Hz)和低频(0.5~10 Hz),其中低频隔振难度最大。本节主要通过降低软体层填充率来获取周期性多层填充桩10 Hz以下的低频带隙。以截面带孔软体层结构(参见图4)为例,圆孔半径设为0.04 m,通过调整圆孔数量来改变软体层填充率。
具体分析前,定义带隙的3个特征参量,即带隙上边界频率(fUBF),带隙下边界频率(fLBF)和带隙宽度(fWBG)。
带隙边界频率及宽度随软体层填充率变化曲线见图6。可知,随着软体层填充率(W)的减小,带隙边界频率及宽度先快速下降,在W= 80%时突变成缓慢下降。以带隙宽度为例,当W> 80%时,拟合直线斜率为0.081 6;当W< 80%时,拟合直线斜率为0.033 5,前者斜率约为后者的2.5倍。这说明填充率越低越容易实现对带隙频率的精确控制,同时说明“低频”与“宽带”不可兼得,开展低频衰减域拓宽研究极为必要。
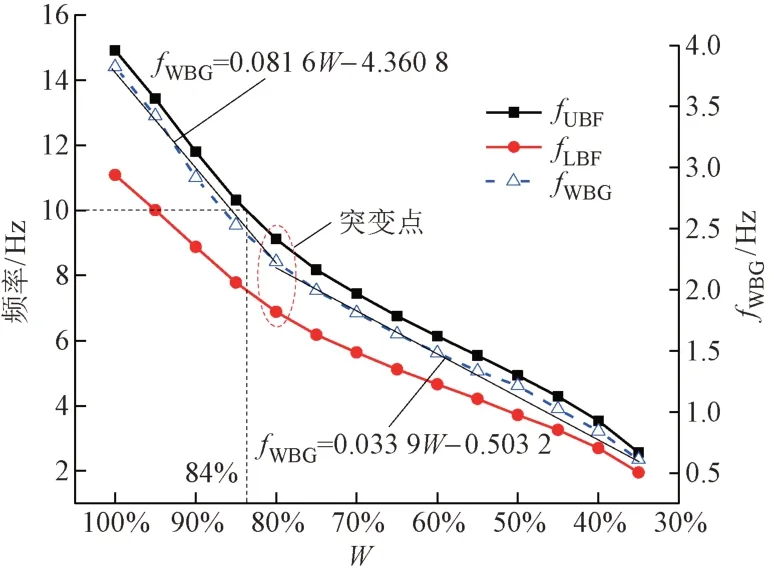
图6 带隙边界及宽度随软体层填充率变化曲线
如图6所示,当频率f= 10 Hz时,W约为84%。因此,为满足10 Hz以下的低频隔振,该结构软体层填充率必须小于84%。不同软体层填充率下带隙边界频率及宽度见表2。可知,W在35% ~ 85%时,带隙频率范围为1.953 ~ 10.312 Hz,约占0 ~ 10 Hz频域的80%。因此,理论上,只要合理配置不同填充率下的多层填充桩,即可满足大部分低频轨道交通隔振需求。
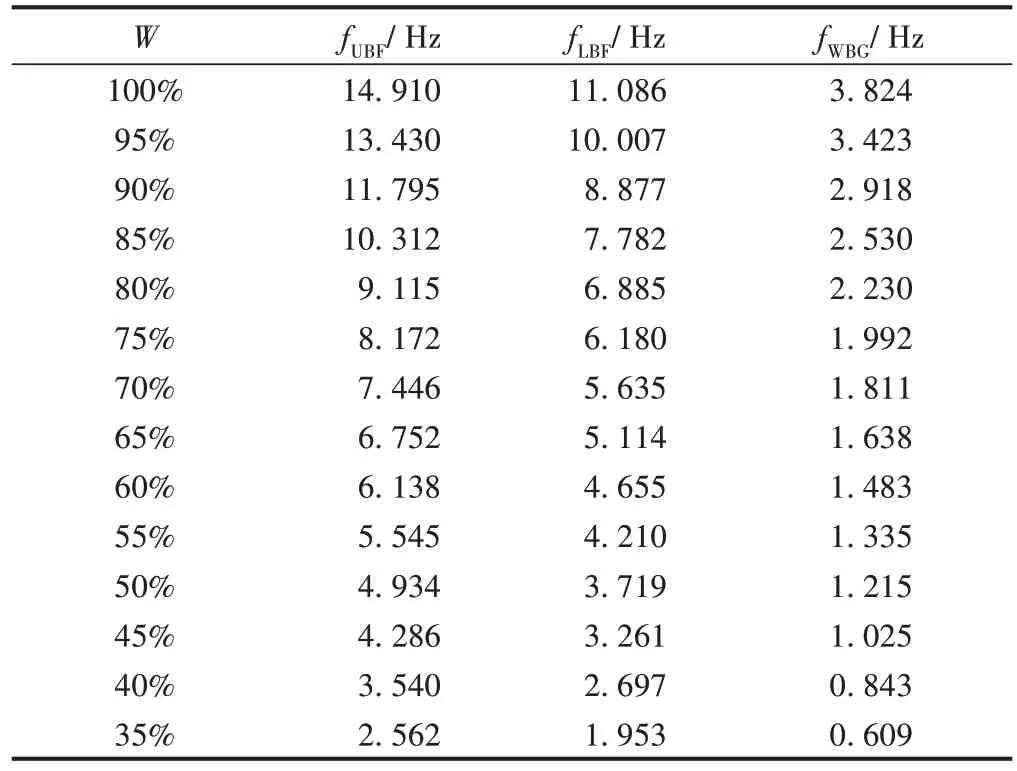
表2 不同软体层填充率下带隙边界及宽度
3 频域分析
6排桩基隔振计算模型见图7,模型上下边界为周期性边界,模型右边界为低反射边界。振源设立于模型左边界,周期排桩设立于振源与被保护区中间。用参照线B和A分别监测有无排桩时的振动位移,通过定义频率响应函数(FFRF)来衡量振动衰减大小,单位:dB。即

图7 有限排桩频率响应计算模型
3.1 桩基排数N影响
以截面带孔型软体层结构为例,在软体层填充率W= 80%时,研究桩基不同排数(N)下的隔振效果,见图8。图中Ω表示衰减域。
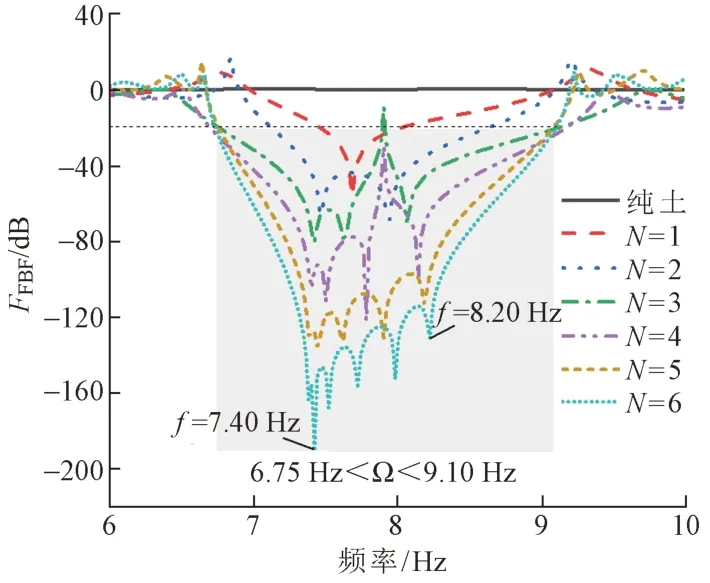
图8 不同排数下频率响应曲线
由图8可知,当排桩数量N= 1 ~ 6时,相对于纯土,有排桩的情况都产生了衰减域,且排桩数量越多,衰减域越宽,振动衰减效果越好。以响应函数FFRF=-20 dB作为振动衰减限值,则当N≥ 3时,衰减域为6.75 Hz < Ω < 9.10 Hz。这与表2中周期排桩计算的带隙范围6.885~9.115 Hz基本吻合,相互验证了求解的正确性,同时说明如果想获得较好的隔振效果,至少要布置3排桩基,这与既有研究结论一致[8,12-13,19]。
3.2 衰减域平稳拓宽方法
如图8所示,当N≥ 3时,随着排桩数量增加,频率响应曲线向下移动,呈沟槽形,其中衰减域中心区域,约占总衰减域的1/3范围,即f≈ 7.4~8.2 Hz,下降最明显。定义衰减域中心1/3频率范围为中心频段。中心频段外的衰减域亦有衰减性,但衰减效果受排桩数量影响非常大,尤其是靠近衰减域边界的区域,几乎只有无限排桩(N→+∞)才有明显衰减效果。由于中心频段范围振动衰减最为明显,因此推测当采用有限排桩组合隔振时,只需满足各类排桩中心频段连续,即可平稳拓宽衰减域。
软体层填充率60% ≤W≤ 80%时中心频段见表3。其中f′UBF和f′LBF分别是中心频段的上下边界频率。可知,当W以5%的增长速率从60%增至80%时,上一桩基的上边界频率f′UBF与下一桩基的下边界频率f′LBF接近。因此以W= 5%为增长梯度时,60% ≤W≤80%区间相邻两桩基中心频段连续。

表3 不同软体层填充率下衰减域中心频段
排桩组合方案见表4。在排桩数量N= 6时,设置8种研究方案。其中方案1为对照组,只包含一类桩,方案2—方案5为二类桩组合,方案6—方案8为三类桩组合。根据连续性假设可知,方案1、方案5、方案8中心频段连续,其余方案不连续。以x和xˉ分别代表二类桩和三类桩中心频段不连续程度,x或xˉ数量越多表示越不连续。
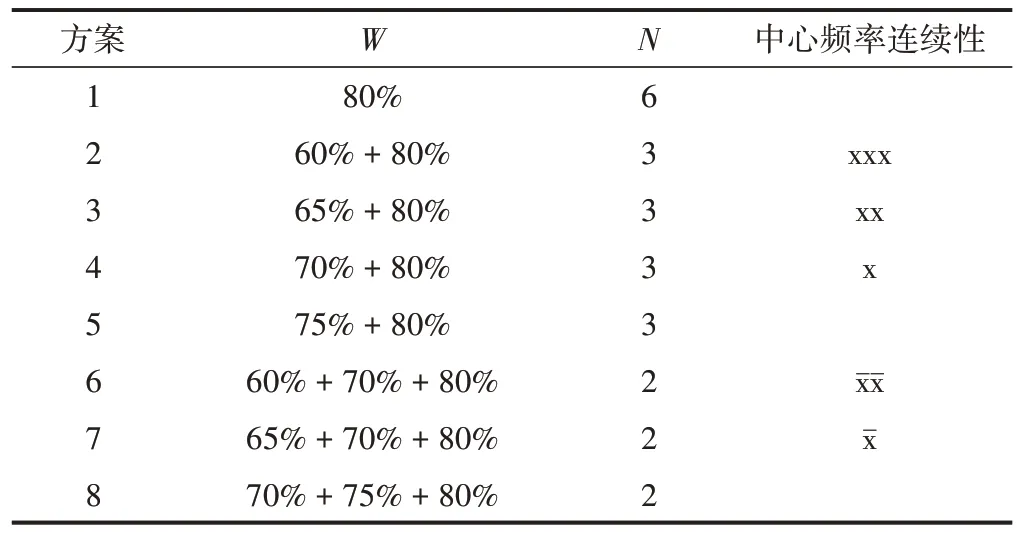
表4 排桩组合方案
不同方案下频率响应曲线见图9。
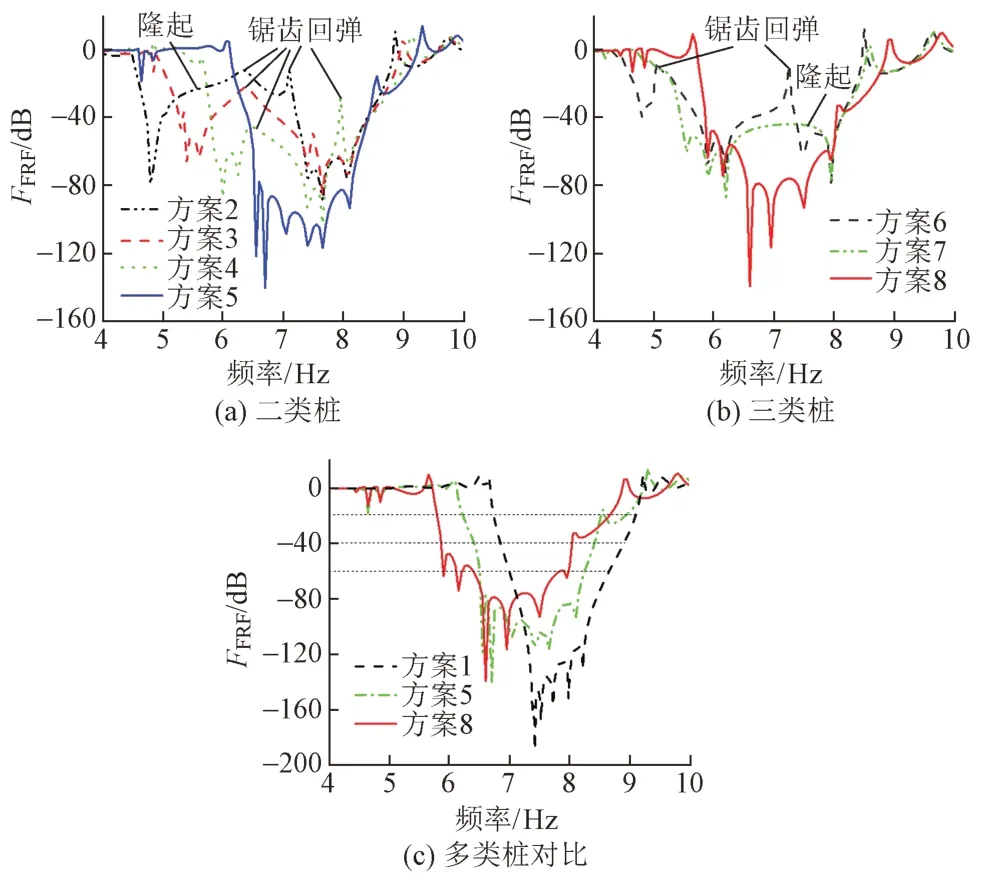
图9 不同排桩组合方案下频率响应曲线
由图9(a)可知,当中心频段不连续时(方案2—方案4),衰减域中心段出现大幅度锯齿回弹或隆起现象,且该现象随中心频段不连续性增加而愈加明显,说明此时衰减域不能平稳过渡,桩基组合效果较差。当中心频率连续时(方案5),衰减域中心段只有小幅度锯齿回弹,外形与单类排桩情况相似(参见图8),整体呈沟槽形,说明此时衰减域能平稳过渡,桩基组合效果较好。
由图9(b)可知:当中心频段连续时(方案8),相比不连续情况(方案6—方案7)衰减域过渡性更好,此结论和二类桩情况一致,进一步证明基于中心频段连续性评价衰减域过渡效果的合理性。相比二类桩组合的情况,三类桩组合时衰减域整体过渡效果更好。以方案2和方案6为例,方案2衰减域中心出现了大范围的隆起和锯齿回弹区,而方案6衰减域中心只出现两个相对较小的锯齿回弹区。虽然方案2和方案6排桩数量相同,且组合排桩填充率W均介于60% ~ 80%,但方案6增加了W= 70%的两根过渡桩基,使得中心频段过渡性更好,因而衰减域过渡更平稳。
由图9(c)可知:随着桩基种类增多,响应函数FFRF增大,衰减域向低频移动且跨度越来越宽。表5为不同方案下各FFRF限值对应衰减域宽度。可知,当FFRF=-20 dB和-40 dB时,方案8衰减域最宽,方案1最窄;当FFRF= -60 dB时,方案5衰减域最宽,方案1最窄。说明相比单类桩(方案1),组合排桩的形式可以拓宽衰减域,且组合排桩类型越多衰减域越宽。
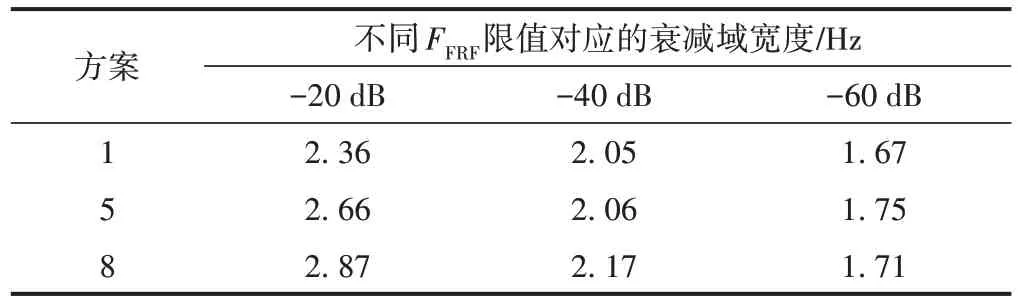
表5 不同方案下各FFRF限值对应衰减域宽度
4 时域分析
根据文献[20],当列车以380 km/h速度行驶时,距离路基30 m之外的地面,其振动频率主要分布在5~9 Hz。本文以6.0、6.5、7.0、7.5、8.0、8.5 Hz为例,通过构建多频率振动函数[Y(t)]来研究组合排桩隔振性[4],即
根据3.2节研究,当选择方案8进行排桩组合时,在5.5~9.0 Hz内形成衰减域。因此以方案8包含本次隔振的所有频率,选择对应的排桩组合方式开展隔振时域分析。不同时刻振动位移见图10。
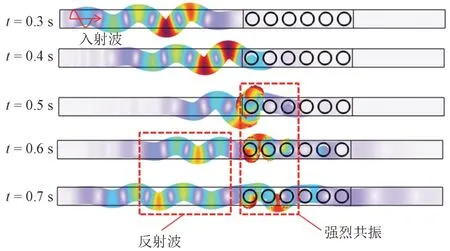
图10 不同时刻振动位移
由图10可知:随着时间增长,入射波从模型左侧激发,并传至排桩隔振区域。在排桩共振作用下,产生了反射波和透射波。从不同时刻振动位移分布可知,当入射波进入排桩区域时,前3排桩发生了强烈共振现象,从而阻断了振动波传播,再次表明前3排桩基是共振隔振的关键。入射波被阻隔后产生了较多反射波,只有少部分振动穿过排桩区域,这是产生隔振效果的根本原因,同时说明组合隔振方式可以对宽频振动产生较好的隔振效果。
5 结论
1)降低软体层填充率可使周期性多层填充桩产生10 Hz以下的低频带隙,且随着软体层填充率降低,带隙频率先快速下降,在软体层填充率为80%左右时改为缓慢下降。
2)当多类排桩中心频段连续时,组合排桩频率响应曲线和单类排桩情况相似,呈沟槽形,衰减域可以平稳拓宽,且组合排桩种类越多衰减域越宽。
3)采用组合排桩隔振时,前3排桩基共振现象最明显。入射波与排桩相互作用后产生了较多反射波,是排桩隔振的根本原因。

