基于毫米波雷达的非视距目标探测和定位方法研究

蒋留兵，张 泽，车 俐

（1.桂林电子科技大学，广西桂林 541004；2.广西无线宽带通信与信号处理重点实验室，广西桂林 541004）

0 引 言

近年来，随着城市化进程的发展，传统窥视镜探测受工作机理的制约无法对建筑遮蔽目标进行探测，由于雷达频段的电磁波具有丰富的透射、衍射、反射等传播特性，利用雷达探测城市环境目标在反恐维稳、灾害救援、智能交通等领域占据重要地位。由于目标通常隐匿在城市建筑中，为了保证我方人员的安全，迫切需要得到遮蔽目标的位置信息，而电磁波不能通过直视路径来探测遮蔽目标，对此基于非视距的路径探测方式得到了国内外的关注。对于非视距（NLOS）目标的检测主要集中在多径利用和穿墙检测这两种典型方法。穿墙雷达是利用低频电磁波检测目标，而多径探测则可以工作在所有频带。因此，大量学者开始关注多径探测技术。

对非视距目标进行探测最早由DARPA 发起［1］。之后相关学者陆续验证了多径信号对非视距目标探测的可行性［2-3］。文献［4-5］主要针对的是单建筑拐角遮蔽目标定位。文献［6］提出多通道扫描雷达系统并基于多通道相位比较算法对墙后目标的位置进行定位。文献［7-8］提出基于匹配子空间滤波法和射线跟踪法对非视距目标进行探测，但两个算法计算量很大。文献［9］提出利用合成双基地雷达基于到达时间的定位方法。文献［10］与［11］分析了拐角多径传输模型，并基于到达时间与相应路径进行匹配，最后通过椭圆交叉定位对目标进行定位，但会发生多径缺失并相应产生多径鬼影问题。此外，文献［12］利用雷达成像算法消除多径鬼影对目标进行定位。文献［13］提出网格匹配的非视距定位方法，需要计算每个网格的到达时间。上述算法多用于提供衍射和高阶反射路径的低频雷达，然而毫米波雷达对于衍射和高阶反射几乎不存在。由于毫米波雷达的便携性以及高距离分辨率，研究毫米波雷达的非视距目标定位算法具有重要意义。

本文首先对L 型建筑下雷达位置和非视距可探测区域间的关系进行分析；之后针对由不同反射面构成的共同可探测区域，设计多路径联合检测器将多条路径的信息联合使用；最后通过实验验证本文所提算法的可行性。

1 非视距可探测区域

本文所考虑的场景是城市巷战及室内反恐环境中的典型场景——L 形拐角；本节将对该场景建立毫米波雷达多径传播模型，并探究雷达位置对可探测区域的影响，提供了雷达布设方案。

1.1 模型构造

L 形走廊的平面二维几何结构如图1 所示，梯形ABCD构成的阴影部分表示NLOS 待探测区域。基于该场景建立直角坐标系，其中x轴与Wall-3平行，雷达R所在位置为坐标原点。Wall-2 与Wall-4之间的走廊宽度为L1，Wall-1与Wall-3之间的走廊宽度为L2。拐角点为C，VR1与VT1分别表示由Wall-1产生的镜像虚拟雷达及镜像虚拟目标，VT2表示由Wall-2 产生的镜像虚拟目标。非视距目标T，通过Wall-1 和Wall-2 反射产生的路径分别记为Path 1与Path 2。

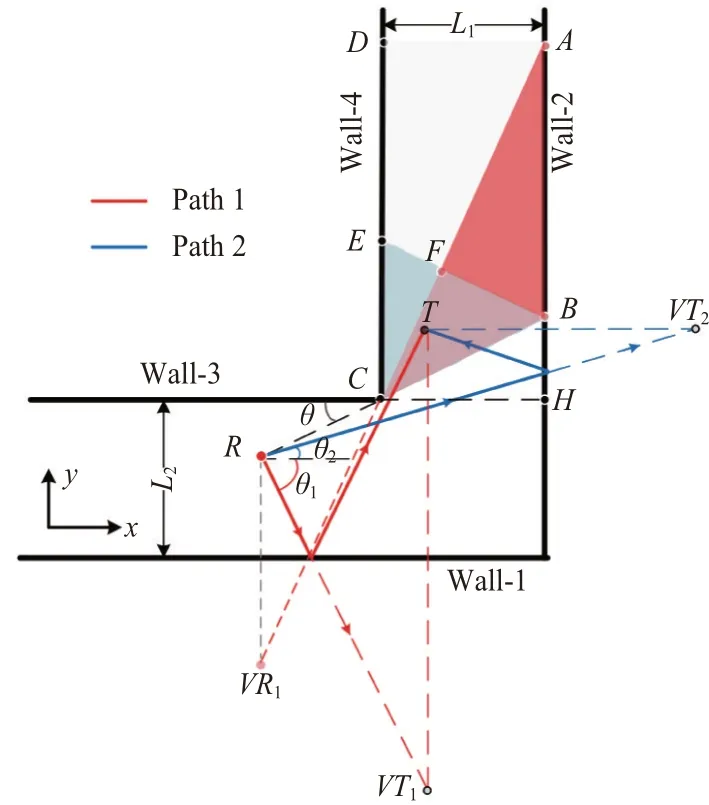
图1 L形拐角多径传播模型

考虑的多径信号是由镜面反射产生的信号，即墙面较光滑。对于毫米波雷达而言，通过阅读大量的文献得出二阶及二阶以上的多径信号衰减严重，本文主要考虑的是一阶多径信号，通过将雷达放置不同位置来对NLOS可探测区域进行研究。

1.2 雷达位置对可探测区域的影响

通常情况下，对非视距区域进行探测时，应该尽可能地保证较大的探测区域，这样能提高对目标的有效探测。然而，非视距可探测区域主要由雷达位置决定。实际应用中，对雷达进行布设，使得待探测目标位于可探测区域内具有重要的研究价值。

如图1 所示，假设雷达R与拐角的连线与x轴负半轴之间的夹角为θ，R与C之间距离为d，则拐角C的位置为(dcosθ,dsinθ)，反射面Wall-1 所在位置的y坐标为(dsinθ-L2)，反射面Wall-2 所在位置的x坐标为（dcosθ+L1）。图中B表示Wall-2上的临界反射点，A表示通过Wall-1产生的临界多径信号与Wall-2 的交点，F表示BE与AC的交点，延长Wall-3交Wall-2于点H。

在走廊宽度足够长的情况下，基于镜面反射原理，当雷达位于（θ,d）处时：

通过Wall-2 一次反射多径信号产生的可探测区域△BCE的面积为

通过Wall-1 一次反射多径信号产生的可探测区域△ABC的面积为

通过Wall-1 和Wall-2 一次反射多径信号产生的共同可探测区域△BCF的面积为

通常，雷达的布设应该使可探测区域的非视距区域最大，即S多边形ABCEF最大，有

式中，

现有对L形拐角非视距探测的研究，仅基于图1 中Wall-2 产生的多径信号进行目标检测定位的研究，其可探测区域仅为△BCE表示的阴影区域，其区域有限，实际探测价值较小。本文采用宽波束毫米波雷达的方法，让雷达发射信号能同时照射到Wall-1与Wall-2，将大大增加可探测区域。为了探究雷达位置及引入Wall-1 多径信号对可探测区域的影响，选取走廊宽度L1= 1.94 m，L2= 2.6 m，θ由10°～60°移动，每次移动2.5°，d在0.5～2 m 之间移动，每次移动0.1 m，通过仿真，得到雷达布设在不同位置时的可探测区域面积如图2所示。

图2 雷达位于不同位置时的可探测区域面积图

由图2（a）可知，对于常规的L 形走廊，若仅通过Wall-2 的反射产生的多径信号探测，通过移动雷达位置，其最大可探测区域约为6.2 m2；若引入Wall-1产生的反射多径信号，其最大可探测面积为33 m2，通过Wall-1 和Wall-2 的反射多径信号产生的共同可探测区域面积为5 m2。移动雷达位置，利用Wall-1 产生的反射多径信号进行探测，将大大提高可探测区域面积。此外，由图2 可知，在相同角度θ下，缩小雷达R与拐角C之间的距离d，将有利于提高可探测区域的面积；在雷达R与拐角C之间的距离d一定时，总的可探测区域随着角度θ的增大而增大。

综上所述，利用雷达进行L 形场景非视距目标探测时，对雷达的布设应该遵从以下规则：在保证目标在雷达非视距的前提下，将雷达与拐角的距离尽可能缩小，雷达与墙面的夹角尽可能增大。

2 多路径联合检测器

由上节可知，利用Wall-1 与Wall-2 反射面产生多径信号进行探测，将大大提高可探测区域的面积，同时，将会形成公共可探测区域，如图1 中ΔBCF所表示的阴影区域。若对位于该区域内的目标进行探测，雷达接收机将收到来自Path 1 与Path 2 的两条多径信号，若能将两条多径信号联合使用，将会提高检测概率。本节中，基于已知的场景先验信息，设计一种多路径联合检测器，旨在对共同可探测区域内的微弱多径信号进行检测并提高检测概率。仿真表明，其检测性能优于单路径的传统检测器。

2.1 提取有效多径信号方法

利用雷达对遮蔽目标进行探测时，回波信号中通常包含大量墙体等固定杂波，从而淹没目标的有效信号，使遮蔽目标探测变得困难。由于墙体是静止不动的，它的多普勒频率为零，而目标是运动状态导致它产生的多普勒频率分量不为零，利用这一点本文采用MTI 技术实现固体杂波的滤除，提取出有效的多径信号。一次对消器的结构图如图3所示。

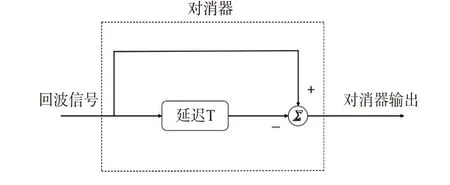
图3 一次对消器的结构框图

2.2 检测器的设计

如图1 所示，位于共同可探测区域的目标，基于毫米波雷达的高分辨率特性，Path 1 与Path 2 的多径信号通常不属于同一距离检测单元。因此，针对该区域内的目标检测问题，可以描述为如下的二元假设检验问题：

式中：ri表示来自Pathi的雷达多径回波；α1与α2分别表示Path 1 与Path 2 的多径回波信号的幅度值；p1与p2分别表示Path 1 与Path 2 对应的阵列导向矢量，其中；wi表示杂波及噪声，假定为独立同分布的复高斯随机向量，均值为0，协方差矩阵M＞0。

假设M已知，α1与α2未知，采用广义似然比（GLRT）方法设计多径检测器。在H0的假设下，r的概率密度函数（PDF）可表示为

在H1的假设下，r的概率密度函数可表示为

由式（7）与式（8）可得对数似然比为

由于α1与α2未知，对其进行估计，估计值如下：

将α1与α2代入式（9）中，得到多路径联合检测器的表达式为

式（10）中的M可用估计的协方差矩阵S替代，S的表达式为

式中，k表示选取用于估计噪声协方差矩阵的训练单元序号。

多路径联合检测器的操作步骤可简要描述如下：

第1步：根据定位精度要求，将感兴趣的区域划分为M×N的网格，将每个网格点的中心坐标记为(xm,yn)，其中m= 1,2,…,M，n= 1,2,…,N；

第2 步：计算每个网格点中心(xm,yn)关于反射面所对应的虚假网格点坐标(x'm,y'n)，并计算(x'm,y'n)至雷达R的距离dmn及波达角θmn；

第3步：根据dmn所在距离单元提取雷达回波数据，得到式（11）中的r；

第4 步：根据波达角θmn计算得归一化阵列导向矢量p；

第5步：由式（12）估计噪声协方差矩阵得M；

第6 步：根据式（11），对每一个网格点计算得到Tmn；

第7 步：将Tmn与门限γ进行比较，若Tmn＞γ，则Tmn所对应的网格点存在目标，且目标位置为(xm,yn)。

2.3 性能对比

为了验证所提检测器的性能优势，采用蒙特卡洛仿真实验，在给定虚警概率Pfa= 10-4的情况下通过检测概率Pd来评估所提检测器的性能，并与文献［14］中的AMF 检测器进行对比。为了控制计算量，进行100∕Pfa次独立的蒙特卡洛仿真实验。在信号强度α1与α2选取不同值时，所提检测器及AMF 检测器的性能曲线如图4 所示。仿真参数于表1中给出。

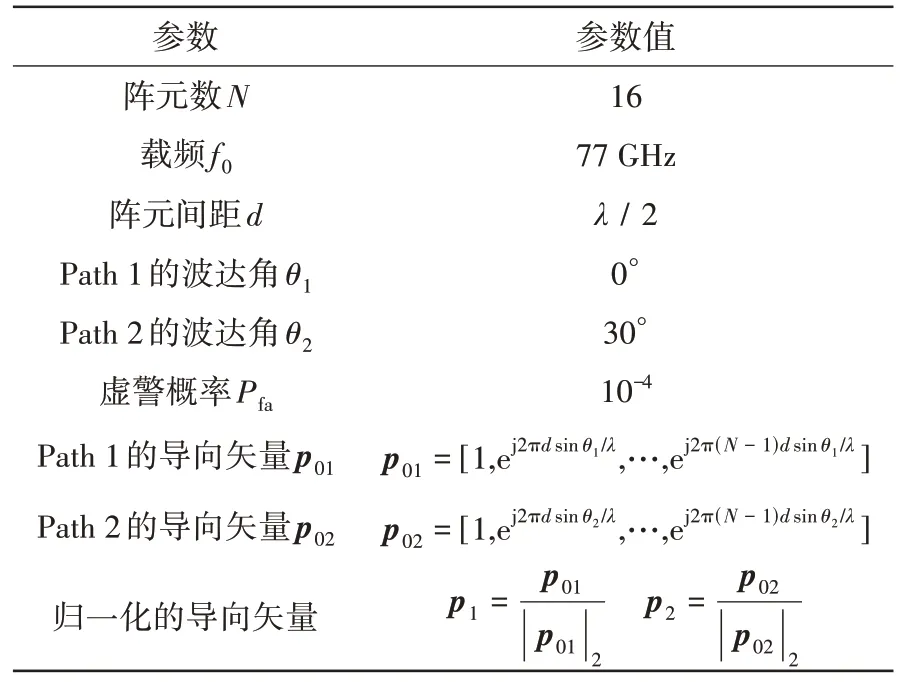
表1 仿真参数表

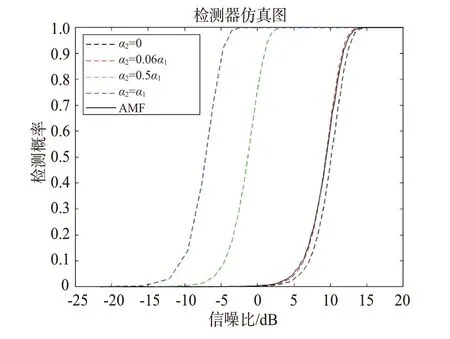
图4 多路径联合检测器与AMF检测器性能对比图

从图4 中可以看出，当α2=0.06α1时，所提检测器与AMF 检测器的性能相似；当α2≥0.06α1时，相同SINR 下，所提出多路径联合检测器的性能明显优于AMF 检测器；当α2=0.5α1与α2=α1时，同等SINR 下，多路径联合检测器的检测性能较AMF 检测器具有较大的性能提升。然而，当α2=0，即第二条多路径不存在时，所提检测器的检测性能较AMF有所下降。

综上所述，在多条多径信号存在时，所提检测器利用包含目标的多条路径进行目标检测，根据不同路径信号强弱的相对关系，检测性能均有不同程度的提高；然而，如果将干扰或者杂波误认为提供目标信息的多径信号，会降低SINR，进而利用本文所提出检测器进行检测，检测性能必然下降（即α2= 0的情况）。

3 实验结果与分析

针对本文所研究的L 型非视距目标检测定位问题，利用所提出的算法展开相应实验。

3.1 毫米波雷达及实验场景介绍

实验设备采用TI 公司AWR1843 车载雷达板和DCA1000 数据采集卡作为收发信号，如图5 所示。实测场景选用桂林电子科技大学南宁研究院A6楼，如图6所示。

图5 毫米波雷达实物图

图6 实验场景图

3.2 实验

为了验证毫米波雷达的多径传播模型及利用多径信号对非视距目标进行检测定位的可行性，通过所提检测器及现有的多径定位算法，在一个L形走廊里采集数据进行实验。选取雷达天线阵列中心所在位置为坐标原点。针对不同的实验目的，进行了如下三组实验，给出实验结果并进行分析。

实验1：雷达布设位置对可探测区域的影响

为了验证毫米波雷达的多径传播模型及雷达位置对可探测区域的影响，对于非视距区域中的微动目标（目标轻微左右摇摆）进行探测，采用二脉冲对消进行动目标显示，再经过二维FFT，得到目标某一时刻的距离-多普勒图像如图7 所示。图7（a）为待测区域及目标所在位置图，目标的所在位置为P（12.7，5），P（21,2）,P（32,2）,P（41.5,4），雷达位置(θ,d)为(30°,1) 。理论上，目标分别位于由Wall-1产生的可探测区域、Wall-2产生的可探测区域、共同可探测区域及不可探测区域；对位于P4处的不可探测区域内的目标，通过移动雷达位置到(10°,0.5 )，并进行重新探测，结果如图7（f）所示。对比图7（b）、（d）或（c）、（d）可知，对于拐角区域内的单目标，通过Wall-1 或Wall-2 产生的一次反射多径信号都能探测到目标，并且当目标处于共同可探测区域时，雷达将接收Wall-1 与Wall-2 产生的两条多径回波（图7（d）所示）；对比图7（e）、（f）可知，对位于同一位置的目标，通过移动雷达位置，可以成功探测到原本无法探测到的目标。综上，通过合理布设雷达，将有效提高对非视距区域隐藏目标的成功探测。

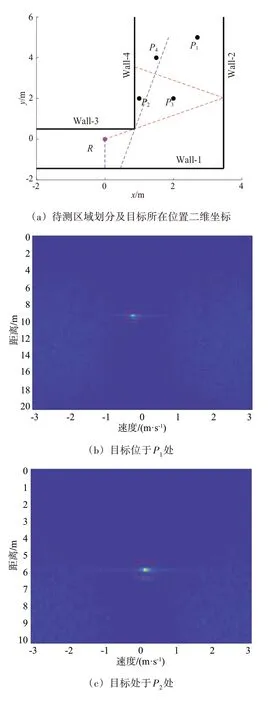
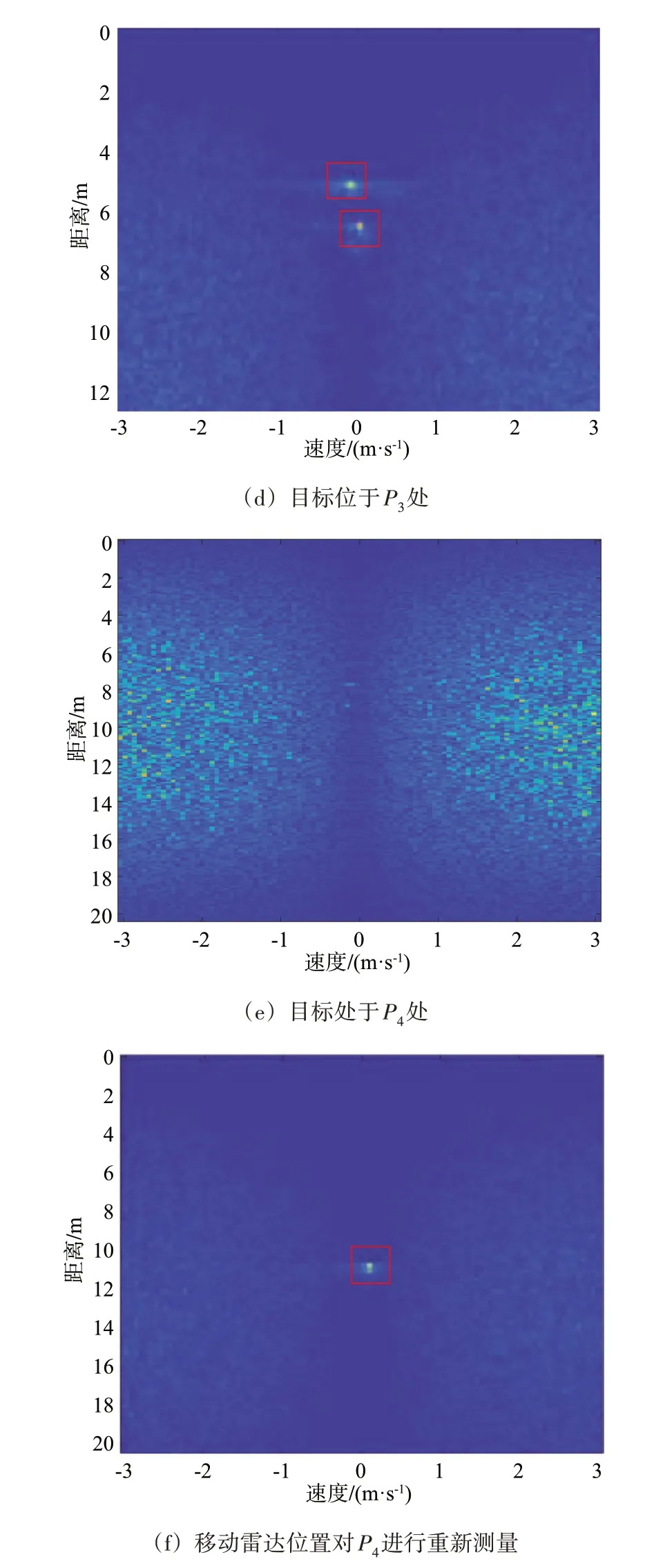
图7 目标处于不同位置时的距离多普勒图

实验2：微动目标定位

针对位于共同可检测区域内的目标，利用所提多路径检测器进行检测定位，数据处理流程如2.2 节所述。实验中，雷达位置为（30°，1），微动目标的真实位置为（2，2），设置感兴趣的检测区域为：X=1～3 m，Y=0.5～3 m，定位精度为0.15 m，即以0.15 m 的间隔将场景网格化。分别用本文所提检测器及AMF 检测器对目标进行检测定位，结果如图8 和图9 所示。由图8 与图9 可知，无论采用多路径联合检测器或AMF 检测器对位于（2,2）处的目标进行检测定位，均可以将目标定位于（2.05,1.867）的位置，与目标真实位置相近。但对比两图可知，采用多路径联合检测器对目标进行检测，由于将多路径联合处理，可以提高目标所在网格点的值，更加有利于检测能量较弱的目标。

图8 多路径联合检测器定位二维坐标结果

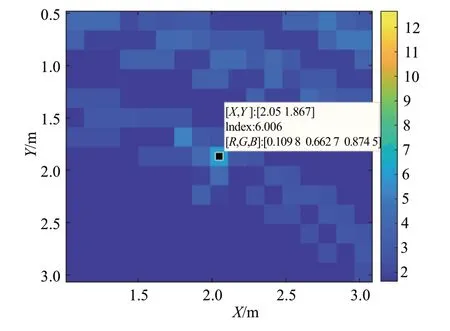
图9 AMF检测器定位二维坐标结果

实验3：运动目标定位

在L 形走廊模拟室内反恐场景，雷达位于（30°，1），目标由（1，2）的位置沿直线行走至（2，2）,再沿直线行走至（2，5）处，基于3.2 节中多路径联合检测器定位方法，采用CA-CFAR 检测，通过DSP进行信号处理，最终的检测定位结果如图10所示。当目标由Wall-2 构成的可探测区域移动到共同可探测区域，再移动至由Wall-1 构成的可探测区域时，雷达将接收到来自两面墙的反射多径信号，因此，利用宽波束雷达同时获取多个反射面的多径信号在实际运用中是可行的；图10 中红线表示目标真实运动轨迹，利用上述定位方法对遮蔽运动目标进行不断定位，考虑到人体反射面积的误差影响，仍可以清晰地得到目标运动轨迹。

图10 运动目标运动轨迹二维坐标实验

4 结束语

本文基于毫米波雷达对L 型非视距区域的目标检测定位问题进行了分析与研究。对雷达位置与可探测区域间的关系进行了理论与仿真分析，给出了雷达布设指南。此外，针对L型拐角非视距研究中存在可探测区域小的问题，提出利用宽波束毫米波雷达同时获取多个反射面的信号提高可探测区域，并通过实验验证了该方法的有效性；其次，对位于由多个反射面构成的共同可探测区域内的目标，基于同一目标不同路径的多径信号均包含目标信息的原理，将多路径联合使用，设计了多路径联合检测器，仿真结果表明，当多路径存在且达到一定强度时，该检测器可以有效提高检测性能，实验表明了该检测器的可行性与有效性；最后，针对非视距探测的实际应用问题，根据2.2 节中的定位方法进行实验，结果给出目标位置信息。