一种适用于低频InSAR的改进空变维纳预滤波算法
夏路福,冯 东,李建鹏,安道祥,周智敏
(国防科技大学电子科学学院,湖南长沙 410073)
0 引 言
干涉合成孔径雷达是一项综合了合成孔径成像技术和干涉测量的遥感技术[1],它通过对不同的下视角或者时间观测同一块地区获取的两幅或多幅SAR 复图像进行干涉处理,得到数字高程模型(Digital Elevation Model, DEM)[2]。InSAR 系统根据工作频段不同分为高频InSAR 系统和低频InSAR 系统,高频InSAR 系统发展较早,相关技术较为成熟[3];而低频InSAR 系统发展较晚,相关技术的研究有所欠缺[4],由于其独有的性质,近年来受到研究人员的关注[5]。
低频InSAR 系统工作在VHF∕UHF∕L 等低频波段[6],其信号能够穿透林叶,该系统可以完成对叶簇覆盖区域的地形精确测绘,在民用和军用领域用途广泛。然而由于信号波长较长,可以穿透植被或者地表浅层等,导致所接收到的回波中杂波较多,噪声较大,干涉处理过程中主辅图像间相干性较差,难以获得高质量的干涉相位图。而高相干性的SAR复图像对是InSAR 干涉测量的前提[7],在InSAR 处理流程中,可以通过预滤波消除一些去相干因素的影响[8],提高图像间的相干性,改善干涉图的质量[9]。
预滤波算法研究中,几乎都是基于高频InSAR数据开展研究,最常用的是公共带预滤波算法[10],该算法认为去相干引起了频谱的偏移,图像频谱中公共部分具有相干性,非公共部分被认为是噪声。公共带预滤波算法在图像频域上进行处理,可以提高图像对之间的相干性,但提升效果较小,且由于一部分频谱被削减,导致图像分辨率降低,进而影响干涉相位图的质量,后续对该算法的研究与改进也没有改变频谱削减的事实[11-13]。Fornaro 等提出了空变维纳预滤波算法[14],它与公共带预滤波算法不同,在图像域上进行处理,不会削减频谱。该算法对相干性的提升较大,但也存在明显的缺点[15],在大尺寸图像上处理时计算量较大,耗时较长,且算法需要未知的干涉相位值作为已知条件,限制了算法的应用。
关于低频InSAR 预滤波算法方面的研究很少,为了得到高质量的干涉相位图[16],本文针对低频InSAR 的回波特点,结合公共带预滤波理论,提出一种适合低频InSAR 的公共带预滤波算法;同时针对空变维纳预滤波算法的缺点,简化算法结构,优化参数估计,并结合公共带预滤波的原理提出一种改进的空变维纳预滤波算法。通过仿真和实测数据验证了改进算法优于传统算法,可以显著提升图像的相干性,改善干涉相位图的质量。
1 低频InSAR公共带预滤波算法
1.1 公共带预滤波算法
公共带预滤波算法处理流程可以分为两步,分别为距离向预滤波处理和方位向预滤波处理,其算法原理如图1所示。
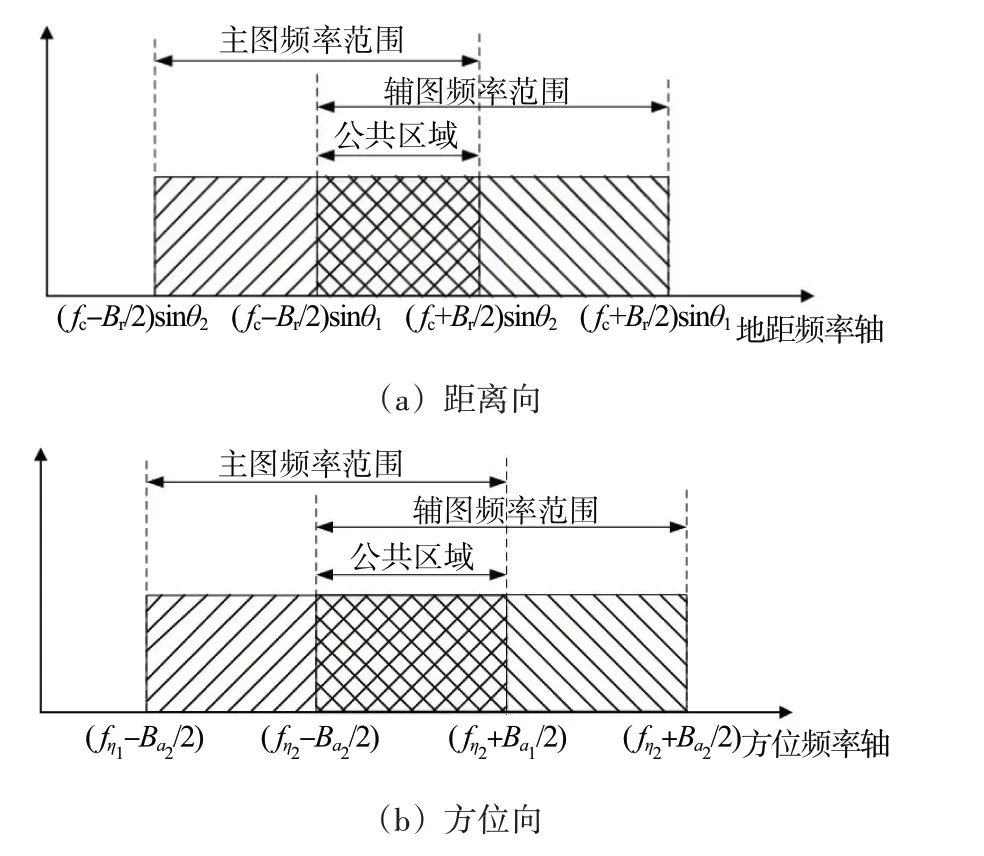
图1 公共带预滤波算法原理示意图
图1(a)为距离向公共带预滤波算法原理示意图,其中fc为系统载频,B为系统带宽,θ1和θ2为两次飞行过程中的入射角。由于基线的存在,造成入射角的差异,导致主辅图像地距频谱产生偏移,通过保留公共地距频谱部分,滤除非公共部分的方式完成距离向预滤波。
图1(b)表示方位向公共带预滤波算法原理示意图,其中fη1、fη2分别为主辅图像的多普勒中心频率,Ba1和Ba2分别为主辅图像的多普勒带宽,图像方位向频谱与雷达斜视角和速度有关,公共带预滤波算法滤除主辅图像方位向频谱中非公共区域,留下公共区域。
1.2 适用于低频InSAR的公共带预滤波算法
以条带模式,正侧视成像为例,SAR 系统接收到的回波二维频谱范围可以表示为[17]
式中,fr为距离向频率,B为系统带宽,fa为方位向频率,va为雷达飞行速度,fc为系统载频,c为光速,Δθ为方位向积累角。
在高频InSAR 系统中,由于相对带宽小,波束角小,图像的二维频谱近似为矩形,且方位向频率范围和距离向频率近似不相关,公共带预滤波时可以分开对距离向和方位向进行处理。而低频In-SAR 系统相对带宽较大,方位向波束角宽度大,其图像的二维频谱为梯形,方位向频谱范围与载频以及距离向频率有关。不同InSAR 系统的回波二维频谱如图2所示。
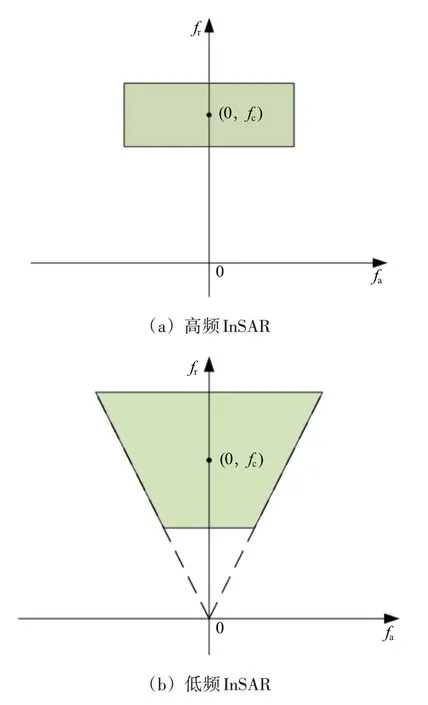
图2 不同InSAR系统回波的二维频谱示意图
由于低频InSAR 的回波方位向频率与距离向频率相关,对其进行预滤波处理时,距离向与方位向不能分开处理,本文结合低频InSAR 系统回波的特点提出一种适用于低频InSAR 的公共带预滤波算法,该算法原理依旧是保留频谱的公共部分,滤除非公共部分,与高频InSAR 公共带预滤波算法的区别在于其直接对图像的二维频谱处理,不再分开对距离向频谱和方位向频谱进行处理。
2 适用于低频InSAR的改进空变维纳预滤波算法
2.1 空变维纳预滤波算法
以一维距离向为例,经过成像、配准后的信号对可以表示为
式中s1、s2分别为主、辅图像信号,r'为距离坐标轴,z(r)为地面散射系数,φ1(r)、φ2(r)为相位,f1、f2为脉冲响应函数,n1、n2为加性热噪声。
假设一条距离线的长度为2N+ 1,将式(2)转化为数学矩阵形式:
以信号S1为例,则其中的参数可以表示为
假设地面散射系数、系统热噪声服从零均值的高斯分布,且三者互不相关。则它们的自相关矩阵可以表示为
式中I为单位矩阵,I2N+1表示(2N+ 1) ×(2N+ 1)的单位矩阵。根据正交化原理,可以推导出滤波器的矩阵形式,如下所示:
在式(11)和式(12)中,
式中ϕinf为干涉相位,可通过主辅图像干涉处理获得。
上述式(11)和式(12)中滤波器的构建,需要知道4个参数即可,分别为距离向雷达脉冲响应函数(f1和f2)、地面散射系数的自相关矩阵σ0I2N+1、噪声功率、干涉相位ϕinf。其中干涉相位ϕinf可通过主辅图像干涉处理获得。距离向雷达脉冲响应函数一般为sinc型函数。地面散射系数的自相关矩阵可以通过信号的互相关求解,如下所示:
同理,噪声功率可以根据信号的自相关求解,如下所示:
通过式(15)求解出参数σ0I2N+1后,代入式(16)中可以求解出求解步骤与求解步骤类似。
空变维纳预滤波算法适用性广,对相干系数提升效果较大,但在实际应用中会产生两个问题:第一,使用该算法进行预滤波时是对一整条距离线处理,构建滤波器以及参数估计时会直接出现大型矩阵的相乘和求逆的情况,计算量较大,计算效率不高,限制了算法的使用;第二,滤波器中干涉相位直接来自未进行处理的干涉相位,其所含噪声较多,干涉相位不准确,最终会影响预滤波效果。
2.2 改进的空变维纳预滤波算法
针对空变维纳预滤波算法出现的问题,本文对该算法的结构进行变化,采用单个像素点进行滤波,可以使滤波器结构从(2N+ 1) ×(2N+ 1)矩阵转变为1 × 1 的矩阵,参数估计也随之发生变化,这样降低了运算的复杂度。
信号对的表达式依旧如式(2)所示,将其转变为矩阵形式:
在式(17)中,以信号S11中各参数为例,可知
上述式子中i表示一条距离线上的某一点,即某个像素点。最终滤波器的结构如下所示:
式中I1为1 × 1 的单位矩阵。式(21)和式(22)的前半段、后半段都为1 × 1 的矩阵,计算量有所减小。同时参数的估计也作出调整,其中距离向雷达脉冲响应函数和干涉相位的求解没有变化,地面散射系数可以直接通过SAR复图像强度获得:
式中A为SAR 复图像强度。则地面散射系数的自相关矩阵σ0I1可直接通过式(9)求解。
对于噪声功率,需要估计每个像素点的噪声功率,上述估计方法不再适用,查阅文献可知[18]
针对第二个问题,空变维纳预滤波算法需要干涉相位作为输入,一般直接采用未进行预滤波处理的主辅图像共轭相乘得到的干涉相位,这样处理会引入含有较多噪声的干涉相位,进而影响滤波器的准确性。而经过预滤波处理后的干涉相位所含噪声减小,因此本文引入迭代操作,以上一次像素点空变维纳预滤波处理后的干涉相位、主辅图像作为下一次像素点空变维纳预滤波的输入,经过一次预滤波处理后得到的干涉相位所包含的噪声较少,干涉相位更加准确,避免了使用含噪声较高的数据,提高了预滤波效果。
最后结合适用于低频InSAR 的公共带预滤波算法,保留公共频谱,滤除非公共频谱可以进一步去除噪声,提升相干性。在不影响图像分辨率的情况下,选择合适的频谱范围作为公共部分,其中频谱公共区域范围可以表示为
式中F2d1为主图像的二维频谱范围,F2d2为辅图像的二维频谱范围。经过公共带滤波处理后,公共区域的频率范围包含了回波的信号频率,保证图像的分辨率不会受损,同时去除非公共带中不相干的噪声,可以进一步提升预滤波效果,提高相干性。本文算法的算法流程图如图3所示。

图3 本文算法的算法流程图
其具体算法步骤为:
步骤1:分别估计主辅图像的噪声功率和IRF矩阵。
步骤2:计算干涉相位,根据公式估计地面散射系数自相关矩阵。
步骤3:构建滤波器矩阵形式并进行像素点空变维纳预滤波。
步骤4:将得到的主辅图像作为输入,重复步骤1~3。
步骤5:根据式(26)以及雷达和场景参数求解合适的公共频谱范围。
步骤6:对主辅图像的二维频谱分别进行公共带滤波,得到最终的结果。
从图3可以看出,所提算法为迭代像素点空变维纳预滤波算法与公共带预滤波算法的结合,其中迭代像素点空变维纳预滤波算法与输入信号的频率无关,而公共带预滤波算法的处理与信号频率相关,当采用高频信号时,将公共带预滤波算法变化为适用高频数据的即可,即分别进行距离向和方位向预滤波处理。
3 仿真数据验证
为验证本文所提算法的有效性,本小节使用仿真数据验证,采用Matlab 软件进行信号仿真,仿真参数如表1 所示,仿真场景如图4 所示,为一个位于平面中心的理想圆锥体。
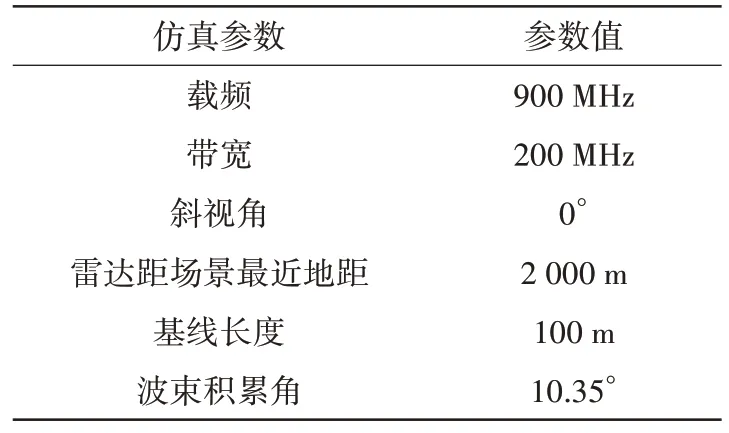
表1 仿真参数表

图4 仿真场景
经过回波信号的仿真后,采用后向投影(Back-Projection,BP)成像算法处理,使用地距成像网格,网格参考高度为0 m。随后对主、辅图像添加高斯白噪声,经过配准得到处理后的主辅图像,如图5所示,它们的二维频谱如图6所示。
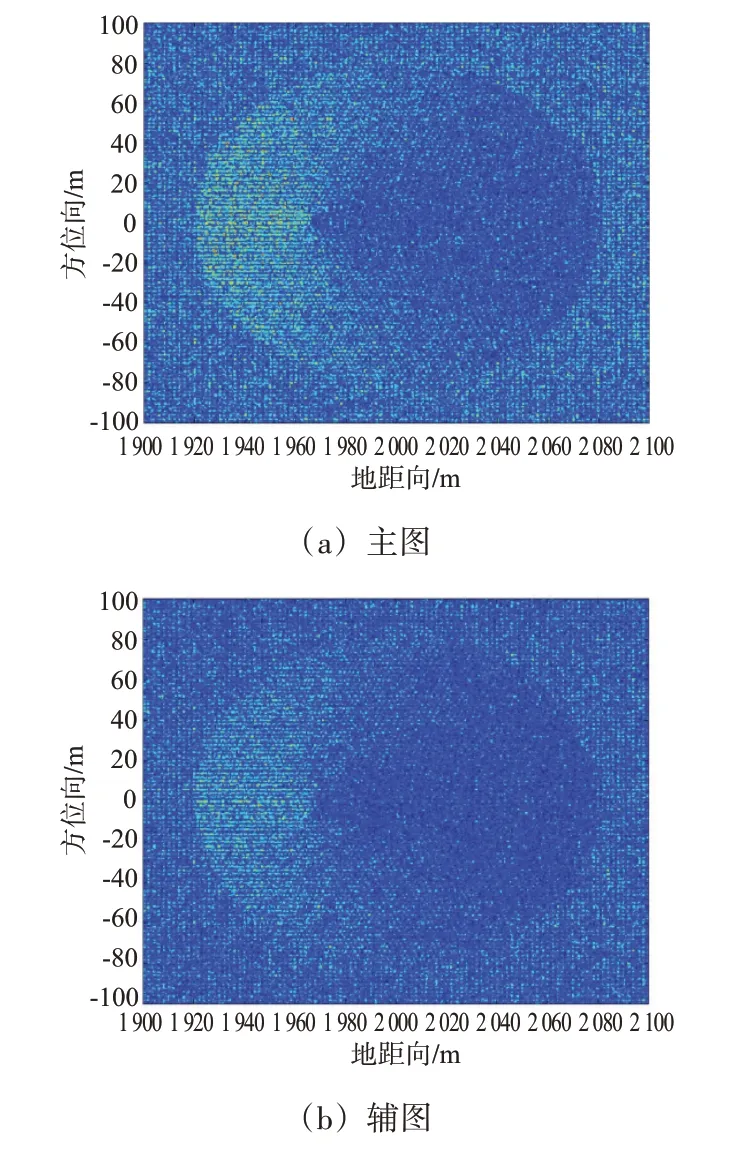
图5 经过配准后的主、辅图像对
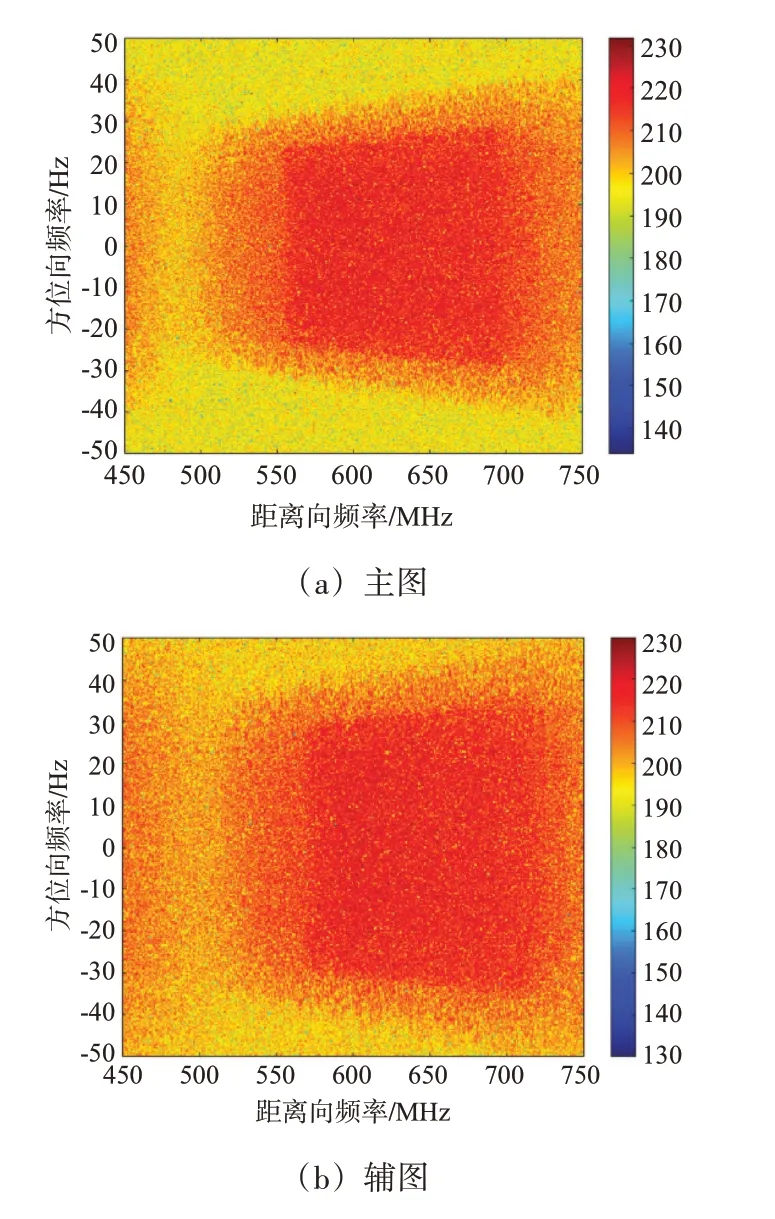
图6 仿真数据二维频谱图
对主辅图像对分别采用不同的预滤波算法处理,其中公共带预滤波算法中公共带区域如图7所示,本文所提算法中噪声功率估计数值如图8所示。
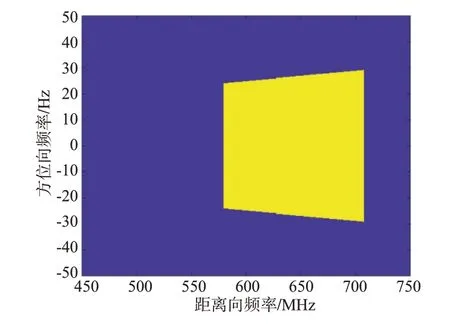
图7 公共带区域

图8 噪声功率估计数值
经过预滤波处理后得到实验结果,其中图9所示为经过不同预滤波算法处理后得到的相干系数分布图,图10 所示为经过预滤波算法处理后得到的干涉相位图。为了观察方便,干涉相位图经过了去平地相位处理。
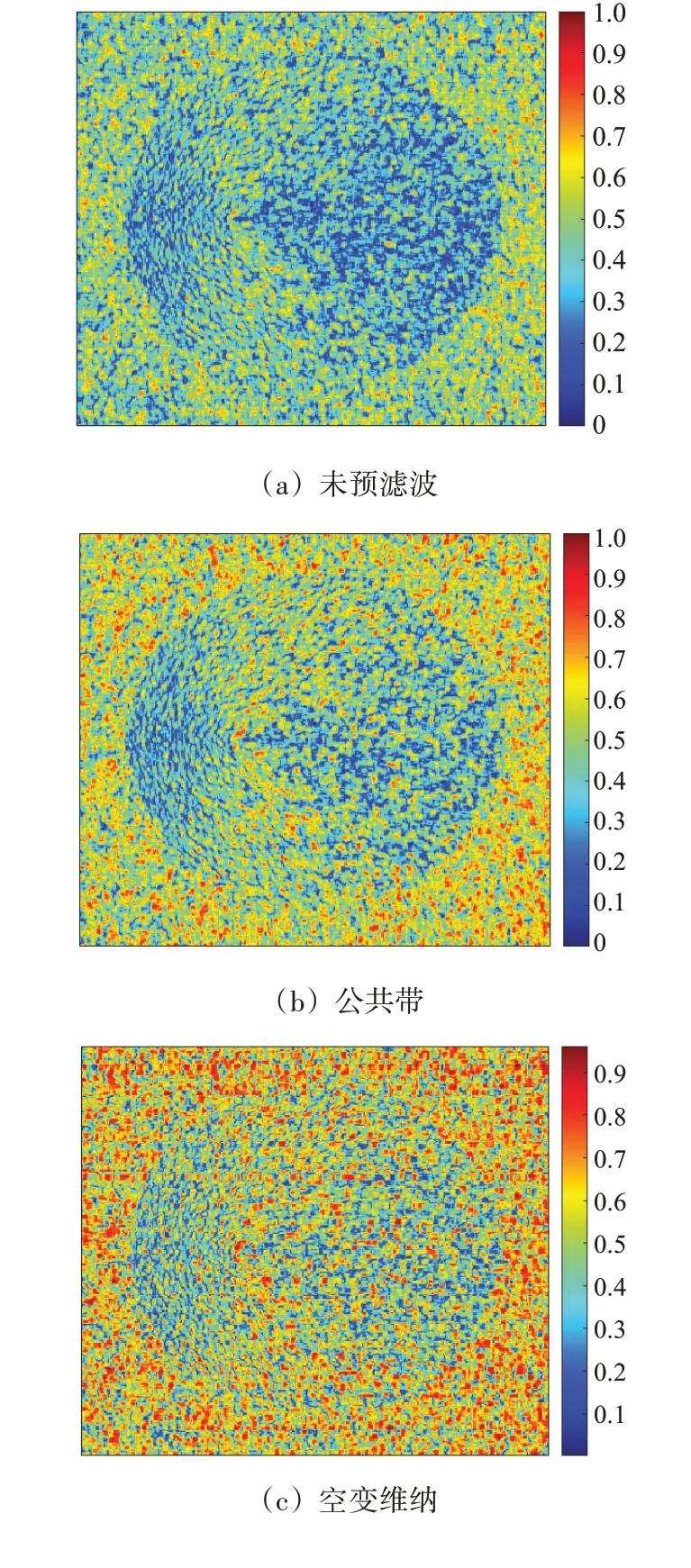
图9 经过预滤波算法处理后得到的相干系数分布图

图10 经过预滤波算法处理后得到的干涉相位图
分析对比图9 中的4 幅图可以发现,经过预滤波处理后,主辅图像间的相干性得到提升,相对于平地区域,圆锥体区域的相干性提升效果较弱,主要由于陡峭的地形与坡度一定程度上会影响预滤波的效果,图9(d)为经过本文所提算法处理后得到的相干系数分布图,可以看出相干系数提升最大,不管是平地区域还是圆锥体区域,相干性的提升十分明显。
观察图10 可以发现,不同预滤波算法处理后干涉相位图的条纹都有所改善,对比圆锥体区域的右侧条纹可以发现经过公共带预滤波和空变维纳预滤波处理后,条纹上面的噪点依旧较多,条纹的清晰度提升不明显;而经过本文所提算法处理后,图像整体变得清晰,相位图上的噪声水平明显比其他算法的低,圆锥体区域的条纹很明显。整体上看,本文所提算法的处理结果目视效果最优,条纹最清晰。
表2 为经过不同预滤波算法处理后的数值结果,观察平均相干系数这一栏可以发现经过公共带预滤波、空变维纳预滤波、本文所提算法处理后相干系数分别提高了0.087 3,0.116 1,0.194 3,客观数据上可以看出本文所提算法对主辅图像间相干系数的提升最大。对比算法的耗时,空变维纳预滤波算法耗时为9.71 s,而本文所提算法的耗时只有5.47 s,可以证明本文所提算法缩短了耗时,提升了算法效率,具有一定的可行性。
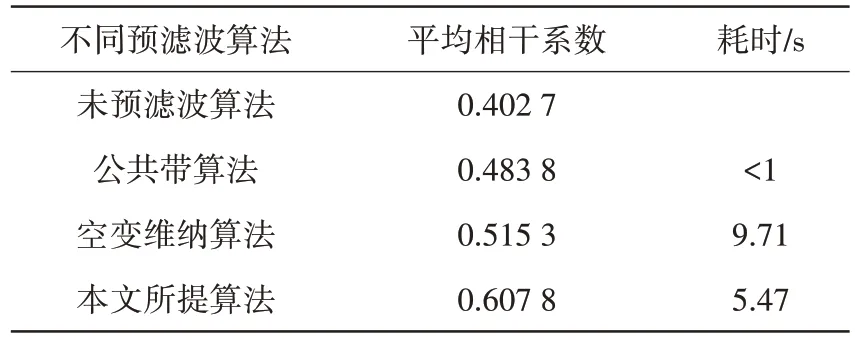
表2 不同预滤波算法处理结果
图11 为相干系数分布的统计直方图,不同预滤波算法处理后的相干系数分布统计曲线分别用不同颜色表示,对比未预滤波处理的曲线,其他曲线明显后移,图像的相干性整体上得到了提升;与其他预滤波算法对比,本文所提算法处理后得到相干系数大部分分布在0.5~0.8 之间,明显高于其他算法的结果,显著提升了整幅图像的平均相干系数水平。

图11 相干系数分布的统计直方图
4 实测数据验证
为了验证所提算法的适用性,本小节采用国防科技大学在2014年通过外场飞行实验获取的机载重轨P 波段InSAR 实测数据,雷达平台高度为3 800 m,基线长度约100 m,雷达离场景中心的最近地距为9 000 m。通过BP算法成像,成像网格为地距网格,选择一个2 305×4 113 像素的典型区域,其中横轴代表地距向,纵轴代表方位向。经过成像与配准后的图像如图12 所示,主辅图像的二维频谱图如图13所示。

图12 实测数据图像
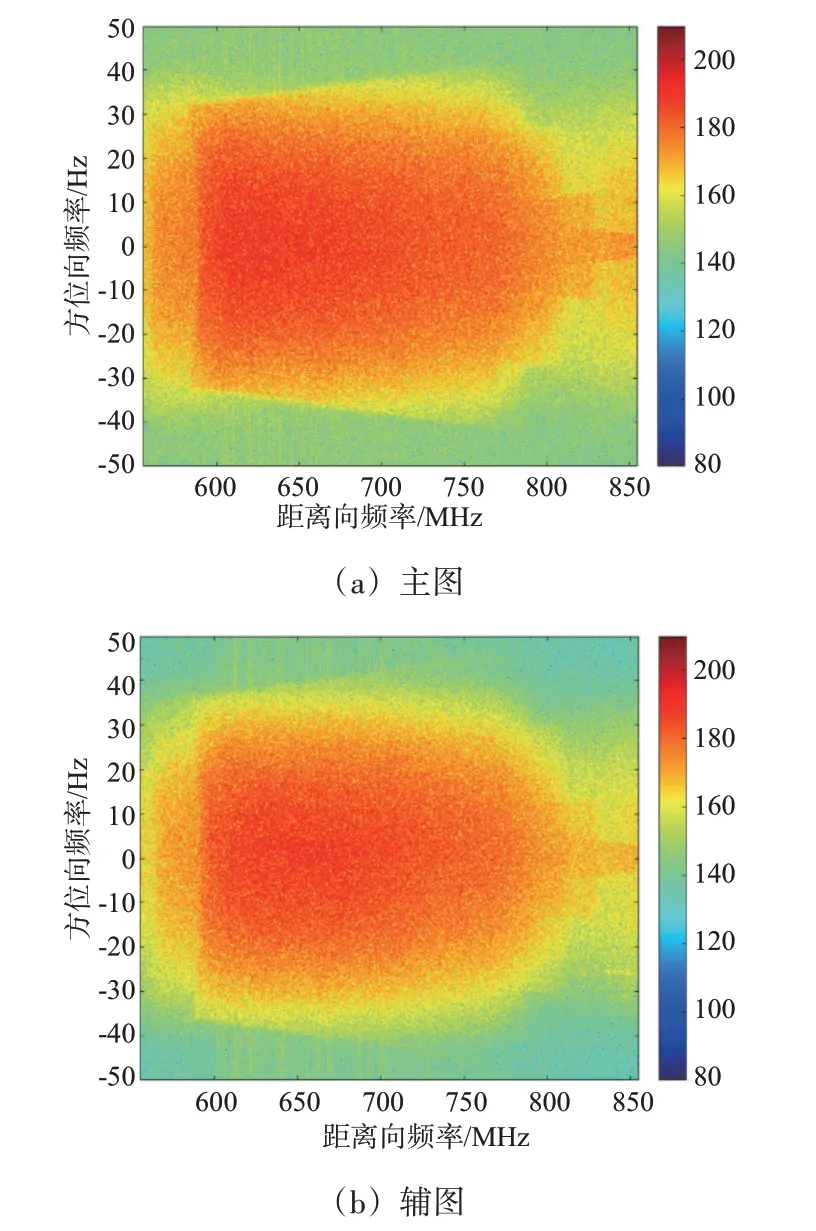
图13 实测数据二维频谱图
对主辅图像进行预滤波处理,其中公共带预滤波算法中公共带区域如图14 所示,本文所提算法中噪声功率估计数值如图15所示。

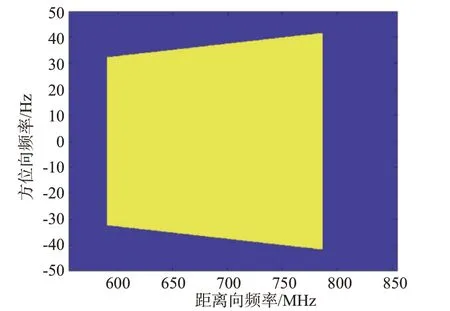
图14 公共带区域
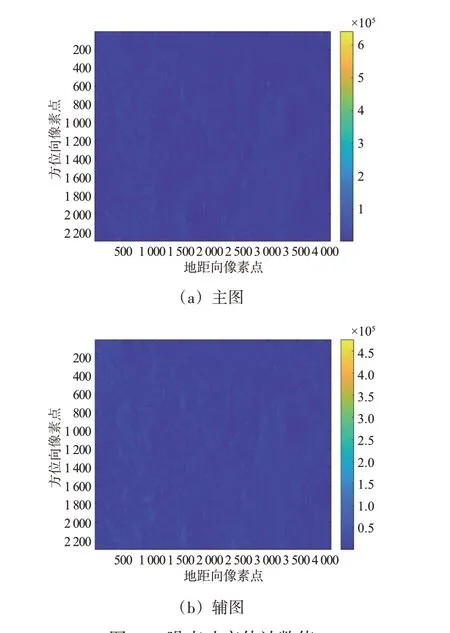
图15 噪声功率估计数值
经过预滤波后的实验结果如图16、图17所示,其中图16 为相干系数图,图17 为干涉相位图,为了方便观察,干涉相位图经过了去平地相位处理。
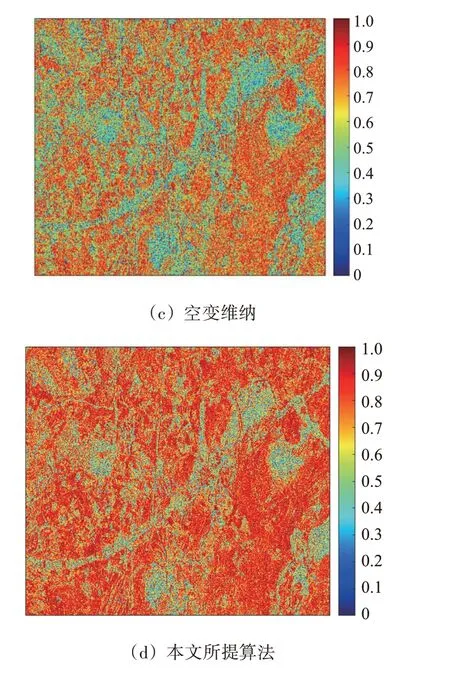
图16 经过预滤波算法处理后得到的相干系数图
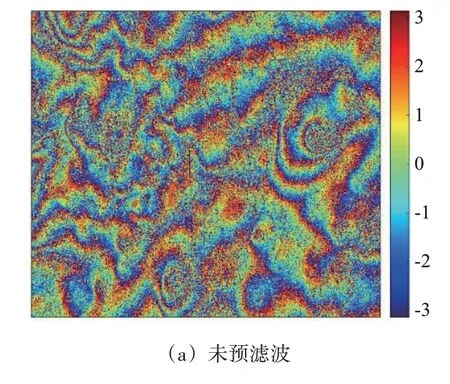
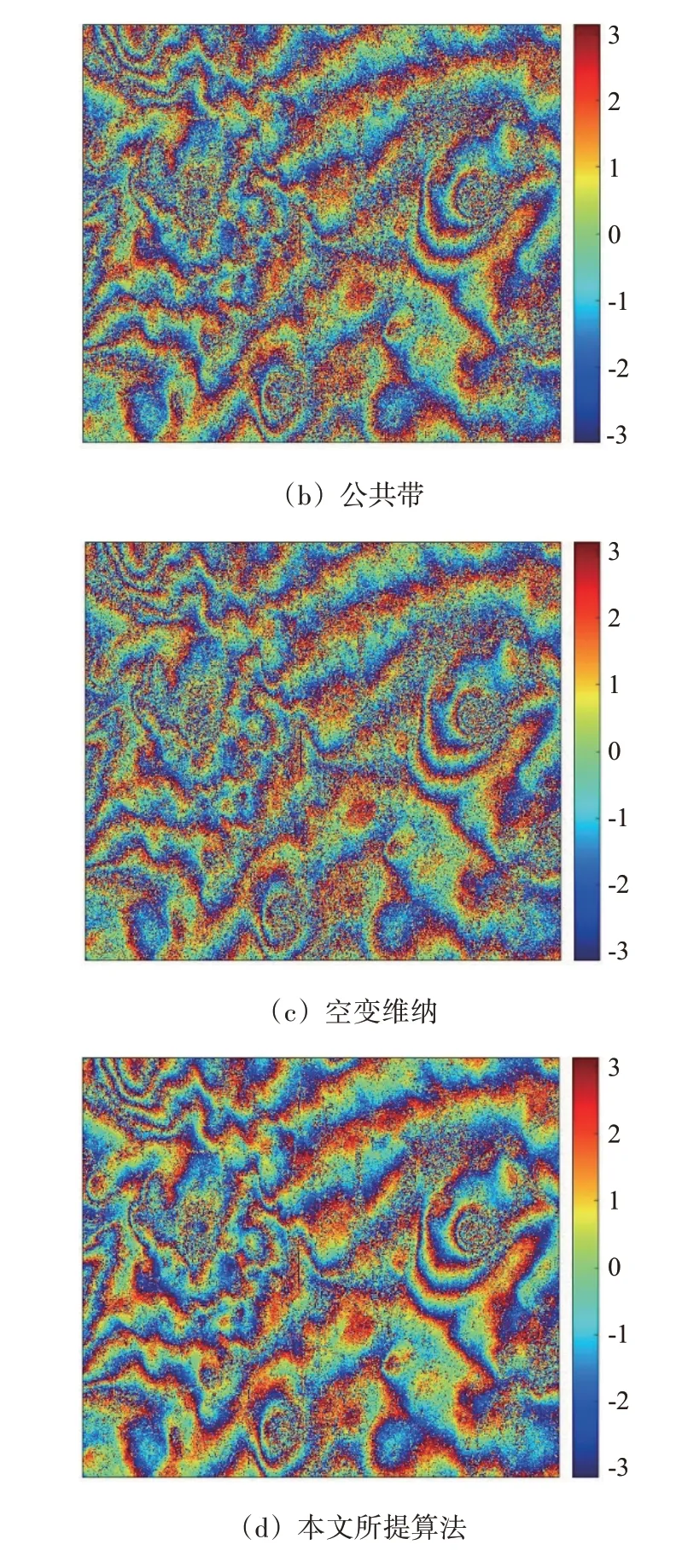
图17 经过预滤波算法处理后得到的干涉相位图
从图16 可以看出,经过公共带预滤波算法处理后相干系数分布图的颜色没有明显变化,相干系数提升不大,而经过本文所提算法处理后,相干系数分布图的颜色加深,相干系数提升较大。观察蓝色的低相干区域可以看出,经过公共带预滤波和空变维纳预滤波处理后,提升效果不显著,经过本文所提算法处理后,这些区域的相干性有了明显提升,提升效果优于其他预滤波算法。
对比图17 的4 幅图可以发现,公共带预滤波算法和空变维纳预滤波算法处理后的干涉相位图噪声有所减少,但是条纹依旧不清晰,上面的噪声变化不明显,而经过本文所提算法处理后的干涉相位图上的条纹更加明显,图像整体的噪声水平下降,其中高噪声水平区域的条纹仍然不清晰。
表3 所示经过不同预滤波算法处理后的数值结果,可以看出预滤波处理后图像对之间的平均相干系数都得到提升,其中经过公共带预滤波、空变维纳预滤波处理后平均相干系数分别提高了0.023 8 和0.081 3,而本文所提算法对平均相干系数的提升达到了0.170 6,提升效果较大。对比空变维纳预滤波算法的耗时,本文所提算法耗时大幅缩减,计算耗时在30 min 左右,计算效率较高,处理较大尺寸图像有一定的实用性。

表3 不同预滤波算法处理结果
图18表示经过不同预滤波算法处理后的相干系数分布的统计直方图,可以看出经过本文所提算法处理后,相干系数分布曲线变化明显,低相干系数的像素点数量大幅减少,高相干系数的像素点数量增多,相干系数统计曲线明显后移,大部分像素点对应的相干系数在0.6~0.9 之间,相干系数整体有所提升。
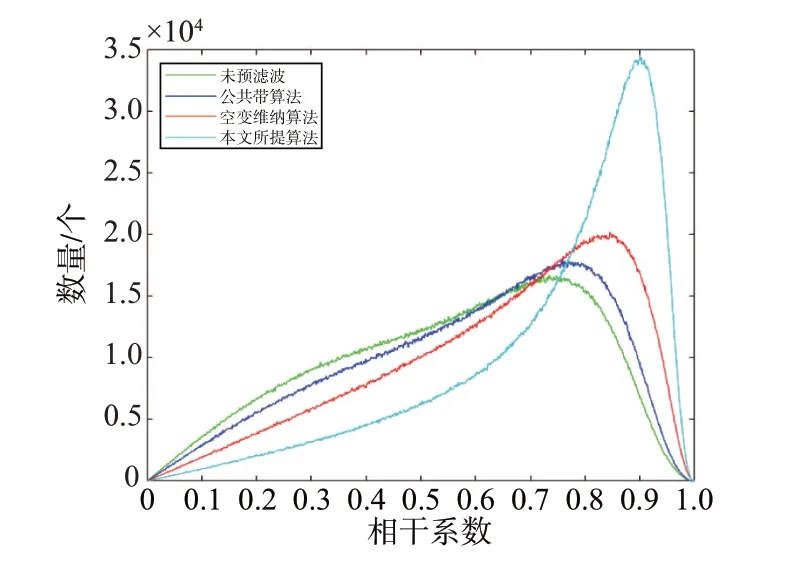
图18 相干系数分布的统计直方图
5 结束语
本文针对低频InSAR 成像特点提出了一种改进的空变维纳预滤波算法,为了增强空变维纳预滤波算法的计算效率以及预滤波效果,本文改进了滤波器的结构,改变了参数估计的方法,避免了大型矩阵的相乘和求逆,提升了算法效率;引入迭代处理,避免直接采用含噪声较多的干涉相位构建滤波器的问题,从而提升了预滤波效果;最后联合公共带预滤波算法,在不损失图像分辨率的情况下去除多余的噪声,进一步提升了主辅图像的相干性。后续通过仿真数据和实测数据的验证,定性和定量分析表明,本文所提算法的性能优于其他预滤波算法,可以显著提升主辅图像间的相干性,改善干涉相位图的质量,具有一定的实用性。

