低年级减法运算的具身性分析
王晶晶 郜舒竹
整数加减法在小学数学课程中具有基础性作用。《义务教育数学课程标准(2022 年版)》要求一年级学生“会20以内数的加减法”[1]。《美国州际共同核心数学标准》也指出:“一年级学生应发展对整数加减法的理解,学习用实物、画图和等式等方式表征问题,并运用20以内的加减法解决有关添上、拿走、合并、分离以及比较等情境的文字问题。”[2]
一、加法与减法的类型
我国数学教学历来注重运用日常生活中的情境帮助学生理解加减法的意义。1992年的一项研究将小学加减法应用题分为四类:第一类是求和或求剩余的部分数和整体数关系的应用题,第二类是求相差数、较大数或较小数的两数相差关系的应用题,第三类是求大数的反向应用题,第四类是比少求和的复合应用题。[3]
从具身认知的角度看,加减法运算涉及操作活动的“变化”问题(如表1)、“部分—整体”问题(如表2)以及“比较”问题(如表3)。其中,“变化”问题可分为加入(添加)和分离(拿走)两类,包含结果量、变化量和起始量三个量;“部分—整体”问题主要涵盖整体未知、一部分未知和两部分未知三种情况;“比较”问题则主要是针对两个对象之间数量的比较,包括求相差量、较小量和较大量这三种情况。
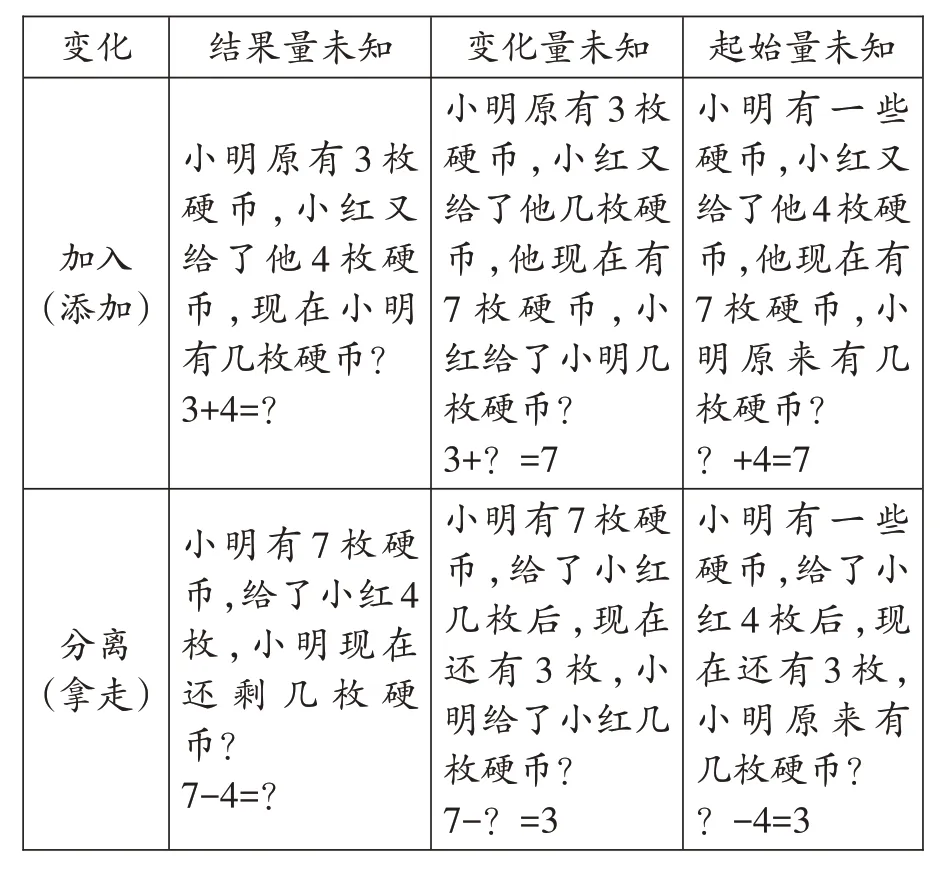
表1 “变化”问题
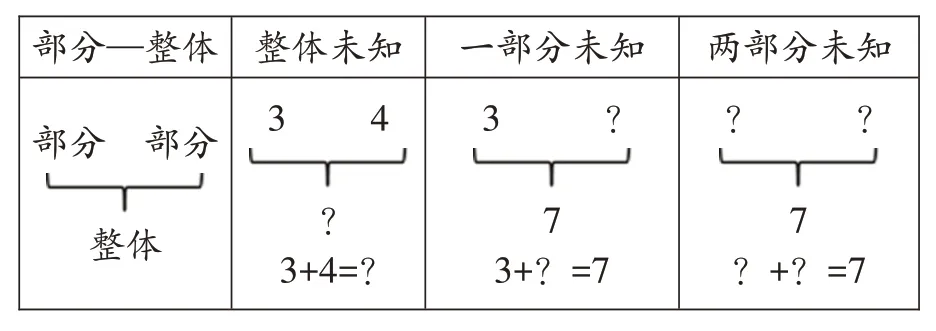
表2 “部分—整体”问题
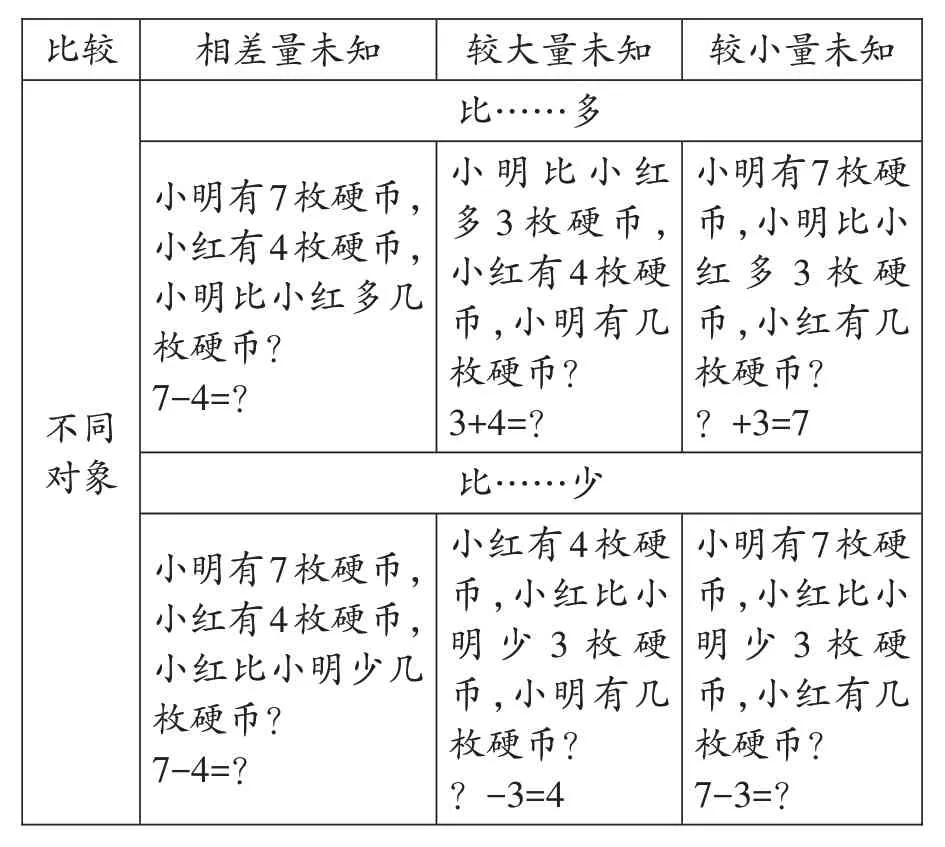
表3 “比较”问题
综上所述,加减法中的数量关系可以分为一个对象变化前后的关系、部分和整体的关系,以及比较问题中两个不同对象之间的关系三类。减法问题类型主要包括拿走(从整体中拿走部分)问题、缺失的加数(想加算减法)问题和比较问题[4]。
二、减法之难
针对学生在减法问题上出现的表征困难,可以从教材编排以及学生认知规律两个方面分析其原因。
(一)教材编排
教材在各年级教学内容中均呈现了减法问题类型。以人教版教材(2023 年版)为例,在一年级学习加减法之前,教材先编排了“比大小”的内容,让学生初步接触对应的数学思想以及两个不同对象间数量关系的比较,为后续解决“比较”问题奠定基础,但并未对这一问题类型进行深入具体的教学。在“5 以内的加减法”中,教材又编排了“分与合”的内容,让学生初步认识加减法中关于“部分和整体”的数量关系,这当中包含一种静态意义上的减法模型。在编排“5 以内的加减法”中的“减法”内容时,教材首先以动态的形式呈现“拿走”这一减法模型,利用气球飞走、人拿走铁锹、小老鼠搬走饼干等动态变化的情境,帮助学生初步直观地建立减法概念,更好地理解减法运算的意义。随后,教材呈现方式由动态变化向静态过渡,通过“四朵小红花,用斜线画去其中一朵”和“两辆车,用圆圈圈出其中一辆车”等问题情境来表现“拿走”。
由此可见,教材中针对减法中“拿走”问题直观操作的教学较多,而关于“缺失的加数”和“比较减法”的教学较少,学生的头脑中还没有形成解决这两类问题的思维图式,所以在遇到相关问题时较难理解,也难以与头脑中的思维图式建立联系。尤其是在“缺失的加数”问题情境中,由于给定的关系转换和组合问题涉及加减法的互逆关系,对低年级学生来说更具复杂性,导致他们极易混淆加减法的意义。
(二)学生认知规律
理解的过程通常涉及三个方面的互动:一是对情境的感知,二是对感知活动无意识的判断,三是符号表征。[5]问题的表征方式主要包括思维表征和外在表征,其中思维表征主要是指在头脑中形成的图式,外在表征则主要表现为图或算式符号等。学生输出符号表征与思维表征的顺序基本一致。因此,学生对减法问题的认知过程一般包括三个阶段:首先,感知问题的自然结构,获取相关信息;其次,在头脑中对问题中的信息进行加工,提取有效信息,并与已有知识建立联系;最后,将感知和加工过的结果用符号表征的形式呈现。
例如,针对“树上原有一些鸟,又飞来了3 只鸟,现在有7 只鸟”这一问题,学生会列出“4+3=7”的算式。这是因为在某些情况下,学生对减法问题的表征受问题结构的影响,而非问题中的数字。对减法问题的表征,即以算式等形式表示情境,类似于具身认知理论中的“隐喻”,遵循同构的对应原则。譬如,学生最先接触的减法问题是“拿走”问题中“还剩多少”这一类型,即已知起始量和变化量求结果量。解题时,学生按照“起始—发展—最终”的顺序,将“起始量、变化量、结果量”与“被减数-减数=差”一一对应。[6]对低年级学生来说,他们的头脑中已经形成了这种从情境到算式同构对应的经验,因此在面对和直觉规律不同的异构情况时,难以自主对问题进行信息加工和关系演变,导致他们即使在一定程度上理解问题中对象之间的数量关系,但是在表征时也可能出现“欲减却加”的情况。
学生对数学符号的理解,与他们头脑中通过现实世界的具身操作所形成的具身经验有关。因此,在选择表征方式时,学生倾向于运用自己已有的思维图式来与问题建立联系,进而进行外在表征。在学生的思维图式中,减法的具身操作表现为“拿走”,加法的具身操作表现为“合并”。题目中的“飞来”在学生看来表示加法中的“合并”,说明他们没能在思维中实现具身动作的转换,这才导致“欲减却加”情况的出现。
综上所述,低年级学生在头脑中缺乏通过现实世界的具身操作所形成的具身经验时,难以实现动作和运算过程的转换,也就无法理解加减法的互逆关系。
那么,如何将算式“7-3=4”与“树上原有一些鸟,又飞来了3 只鸟,现在有7 只鸟”的情境建立符合学生认知规律的联系?原题中,“飞来”就是“增加”,与符号表征“4+3=7”具有同构对应关系。而“7-3=4”需要学生想象反向过程,即撤销转变,进而“减少”的过程。这是一个互逆的过程(如图1),用算式表示为“4+3-3=7-3=4”。理解这种加减运算之间的互逆关系,对学生在计算过程中运用转换思想至关重要。
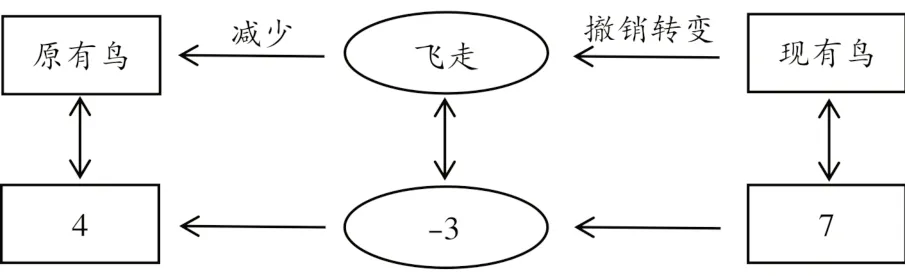
图1 互逆过程示意图
三、逆运算的动作与理解
算术教学要考虑学生在解决问题时所面临的两个认知需求:一个是如何高效准确地进行算术计算,另一个是如何选择合适的算术运算来解决特定问题。前者可称为“数值计算”,即对数字进行运算,如加法求和与减法求差,依赖于学生对数字间关系的理解;后者则称为“关系计算”,关注情境中数字间关系的转换和组合。这两种计算既相对独立,又相互关联。[7]在数值计算中,相同的数字间存在多种关系。以“7-3”为例,第一种情况为“树上原有7 只鸟,飞走了3 只”,是学生较为熟悉的一种情况,它接近减法的初始概念,即“拿走”,较少涉及关系计算。第二种情况为“飞来了3 只鸟,现在有7只”,更贴近学生所接触的加法概念。要让学生将此问题理解为减法问题,就要让他们意识到关系的变化,即“飞来了3 只鸟”,并思考通过何种变化可回归初始状态,即“树上原来有几只鸟”。因此,学生需要理解变化的逆过程,即撤销转变。加减法的互逆关系与数值计算以及数学问题中数量的分析密切相关,是数值计算和关系计算的重要方面。其中,学生较难理解的就是数学运算中的关系计算。
互逆(Inversion)是数学中结构研究的基本关系组成部分,也是人类个体经验和社会经验的基本关系组成部分,与平衡(Equilibrium)、不变性(Invariance)、撤销(Reversal)、补偿(Compensation)、对称(Symmetry)、抵消(Balance)和守恒(Conservation)等诸多关键要素密切相关。[8]涉及互逆的概念包括互逆原理(Inverse Principle)a+b-b=a、相减否定原理(Subtractive Negation Principle)a-a=0、相减恒等原理(Subtractive Identity Principle)a-0=a、互补原理(Complementary Principle)a+b=c等价于a=cb。[9]这些概念在加减法运算中也有所体现。
在纯形式算术中,加法和减法之间的互逆关系对计算的灵活性与高效性以及学生理解程度的评估具有重要意义,同时,也会对学生计算技能的发展产生影响。这种互逆关系主要包含三种情况:分解、顺序(想加算减—间接加法—补偿)和捷径(a+b-b=a)。[10]第一种情况是分解(Decomposition),要求学生理解进位和退位的过程,以便掌握加减法之间的互逆关系。其中,减数“守恒”对学生来说较难理解。如512-28,从12-8可知,减数从十位上减去1 个十,同时在个位上以10 个一的形式加上10,数值仍保持不变。第二种情况是顺序(Sequential),即学生熟悉的“想加算减法”,意思是当数字彼此接近时,可用加法来解减法。如52-49,学生可以从49 开始数,即将52-49=3 转换为49+3=52,体现了互逆关系中的互补原理。这种用加法来解决减法的方式称为间接加法,而运用这种间接加法来解决减法的则称为“补偿”。第三种情况在日常进行口算时较为常用,可以称为逆捷径策略(Inversion Shortcut Strategy)。如88-19,其常见描述为88-(19+1)+1,即88-20+1,这种无须计算便可直接得出答案的策略,就是运用了互逆原理a+b-b=a。
选择正确的计算方法进行数值计算是检验学生是否理解加减法互逆关系的重要标准,而选择正确的算术运算方法解决问题则是学生获得概念的重要途径,这揭示了学生在心理上执行的关系的构成。关系计算是学生学习的难点,当遇到涉及情境的算术运算时,学生应考虑其中是否有关系计算。比如在减法的“拿走”问题中,若所求为结果量,便与学生最初接触的减法概念紧密相连,无须进行关系计算;若所求为起始量和变化量,涉及加减法的互逆关系,就需要进行关系计算。在加减法情境问题中,当学生能够利用6+2=8 推理出8-2=6(或8-6=2)时,就表明他至少有意识地援引了a+b=c→c-b=a(或c-a=b)的代数互补原理。这种“关系演算”就是算术和代数间表达的核心,而要理解这些关系计算,学生就需要亲身经历转换过程。
四、在具身动作中形成思维图式
勒内·笛卡尔(René Descartes,1596—1650)曾提出“身心二元论”,认为人的心智和肉体是相互独立的。随后,莫里斯·梅洛-庞蒂(Maurice Merleau-Ponty,1908—1961)提出“具身的主体性(Embodied Subjectivity)”概念,强调人不是一种离身的心智,不是笛卡尔所谓的“纯粹思维”,更不是“复杂的机器”,而是通过身体与世界互动的创造者。认知心理学领域由此迎来了一场以“具身认知(Embodied Cognition)”为核心的变革。美国的乔治·莱考夫(George Lakoff)和马克·约翰逊(Mark Johnson)提出了具身认知理论的相关观点。这一理论主要源于认知科学的三个主要发现:一是人的认知是“具身的(Embodied)”,二是人的思想(Thought)往往是“无意识的(Unconscious)”,三是对抽象概念的理解大多依赖于“隐喻(Metaphor)”。[11]
具身认知理论认为,人的认知来源于头脑、身体与环境的互动。在这一过程中,个体会在头脑中形成思维图式,也称为“意象图式(Image Schema)”,并将其应用于相关活动之中。[12]5由此可知,对抽象概念的理解需借助具体的操作活动,而具身活动的开展有利于学生理解减法运算的意义。因此,教师要帮助学生通过具身操作在头脑中形成关于逆运算的思维图式,从而理解运算的意义。
运算的意义不仅在于从算式到结果的“算(Calculation)”,更在于人的“运(Operation)”,也就是涉身的动作。“加(Addition)”和“减(Subtraction)”作为运算的互逆关系,从认知的角度看,涉身的动作有很多,所以要理解加减法的互逆运算,关键就在于重视动作和运算过程的转换。例如,可以利用容器图式中“放入”和“取出”的操作进行隐喻,将“加”视为向容器中“放入”的动作,“减”则表示从容器中“取出”的动作,“放入”和“取出”这两个动作具有“互逆”的关系。[12]6比如,盘子中原来有a个苹果,再放入b个苹果,即“a+b”,再从盘子中取出b个苹果,即“a+b-b”。经历放入再拿出这一过程后,盘子中的苹果数量与初始状态一致,即“a+b-b=a”。同样,也可以通过路径图式中人脚“前进”和“后退”的行走动作来隐喻加减法的“加”和“减”。从起点前进,然后后退相同的步数,人就又回到了起点。诸如此类具身活动,均可成为隐喻加减运算互逆关系的具身经验。而这种“加”与“减”的互逆关系,则是沟通这两个运算的基本规律。[13]因此,对于抽象的数学符号“a+b-b”,可以利用容器图式和路径图式中的动作来表示隐喻。教师要帮助学生在具身操作中理解运算过程中相同数字的加减法是相互抵消的,熟练掌握并运用a+b-b=a的运算形式。这有助于学生进一步理解逆运算,从而将对加减法互逆关系的理解从表面学习提升至深度学习。
运算的意义的理解过程始于现实世界的具体操作,再转化为思维世界的图式,最后用符号进行表征。在课堂教学中,教师应通过与运算有关的具体操作来表示隐喻,引导学生模拟操作,并反复进行相似的实践。在这一过程中,学生的主体认知与外界环境产生互动,从而构建起关于运算的意象图式,即形成关于加减法互逆关系的具体经验。这有助于学生深入理解逆运算的意义,使其能根据具体情况选择合适的算术运算进行表征,以证明其对运算意义的理解。而学生运用数学符号表征问题的主要目的在于理解符号的价值,当学生再次看到相关符号时,头脑中会形成一种思维倾向,即与符号有关的具体操作。只要他们付诸行动,就意味着其不但理解了符号的意义,也理解了运算的意义。
综上所述,本文重点分析了学生在减法问题上出现“欲减却加”现象的原因,提出理解减法运算需要在具身操作中把握加减法的互逆关系,并对加减法情境问题进行了合适的表征。小学数学中,不仅有加减运算的互逆关系,还包括乘除运算的互逆关系。教师要利用日常生活经验,如弄脏衬衫后通过清洗使它恢复到原来的状态,从罐子里拿出三块饼干后再放入三块饼干数量不变,或者通过具体操作来表示隐喻,帮助学生理解互逆关系,提高学生的运算能力,培养学生用数学的思维思考现实世界的能力。

