基于AES的改进视频加密测试
杜宸罡,李 博,画芊昊
(中北大学 仪器科学与动态测试教育部重点实验室,太原 030051)
0 引言
随着互联网技术的发展,视频加密技术[1]如同一把锁,保护好自己的贵重物品显得格外重要,广泛应用于军工、航天、生物医疗、互联网、体育比赛等诸多领域。AES加密是目前H5时代广泛使用的技术,该加密是建立在HTTP之上,设计简单,只需要很少的存储器,因此使用简单,接入代价小,可以抵抗所有一致的攻击,在多个平台上速度快,编码紧凑,有利于CDN加速技术[2]的实施,其最大的优点便是几乎主流的软件都支持,包括微信、qq等,打开就能播放,兼容性很好,但AES加密算法本身最大的缺点便是由于算法是公开的,如果不能保护好密钥的文件,ffmpeg等命令行,很多工具软件均可拿到密钥对视频基本还原。对于该问题,Ajish等人[3]提出了一种基于小波的AES算法,加快了加密过程,降低了移动设备的CPU利用率,从而增加了加密的安全性能;Yiding等人[4]提出了一种内存处理架构AESPIM将AES加密计算卸载到内存端,通过显著减少数据移动和增加内存带宽,从而提高了加密的安全性能;Ke L等人[5]提出了一种新的32位可重构、紧凑的AES加解密结构,并在非bramFPG中实现,还提出了一种新的复合域GF((24)2)上的子流水线动态密钥调度方法,可以同时生成圆密钥,进而提高了安全性能。然而,本实验在原有AES算法的基础上,先是利用RANSAC算法将误匹配消除,然后引入2DLogistic映射与2D-DCT的数字图像隐藏技术[6],经实验对比分析,密钥敏感性、视频质量、运行效率均得到了明显更加良好的数据体现,从而使得本文改进后的AES算法更具有安全性,从而使得实验更有意义。
1 AES的视频加密技术基本理论
AES是一种SPN结构[7]的高级加密标准的视频加密技术,其过程是由多个轮次进行,每个轮次均经过SubByles、ShiftRows、MixColumns、AddRound Key这4个步骤,即字节代替、行移位、列混淆和轮密钥加。
2 AES加密算法的分析与改进
2.1 加密元素的选取
轮密钥加可以看成S0 S1 S2 S3组成的32位字与W[4i]的异或运算,由于是异或运算进行语法元素加密,但方法简单,容易被破解,安全性不高,所以二值化是处理比较好的一种方法。二值化的方法有很多,比如:定长二进制(FL)、截断莱斯二元化(TR)、截断一元二元化(TU)、K阶指数哥伦布二元化(EGK)、一元二元化(U)等等,一元码只有在非负整数时才可以使用,截断莱斯二元化加密时必须知道CMax和R的值,K阶哥伦布指数对语法元素具有可塑性,但过程相对复杂,需要完成前缀码和后缀码的加密,定长二进制只需要满足选取的语法元素分布均匀即可,因此,此处选取定长二进制方法将轮密钥加步奏进行二值化较为合适。
字节代替是字节求一次乘法逆再完成一次仿射变换[8]而完成,使得共同点变为共线点的双射,平行直线变为平行直线,保持共线三点的简单化,从而保持俩平行线段的比值不变。在求乘法逆方法中,欧拉定理求逆元需要任意互质的q,p恒成立,且该方法需要多算一个欧拉函数;费马小定理具有局限性,需要p为质数;扩展欧几里得该方法需要先求出xx、yy方程的一组整数解,计算量较大。根据平时计算经验,线性求逆方法(递推法)最好,适用范围较广。线性求逆元方法如下:
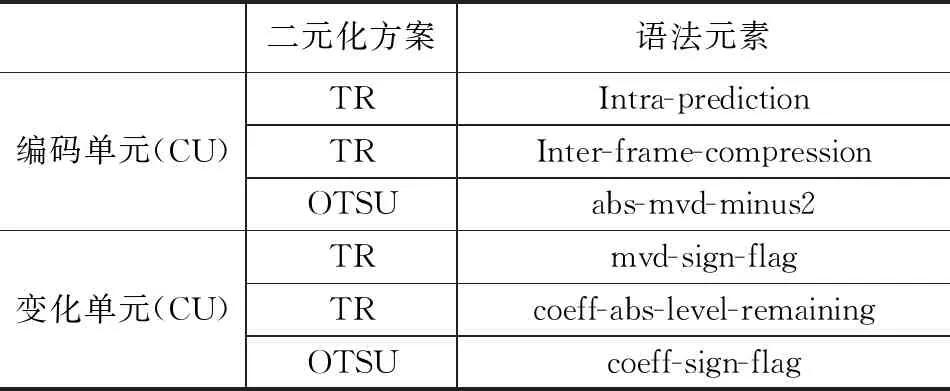
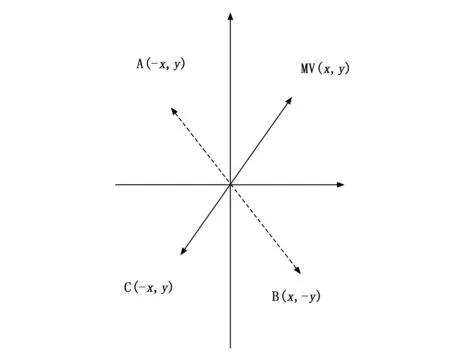
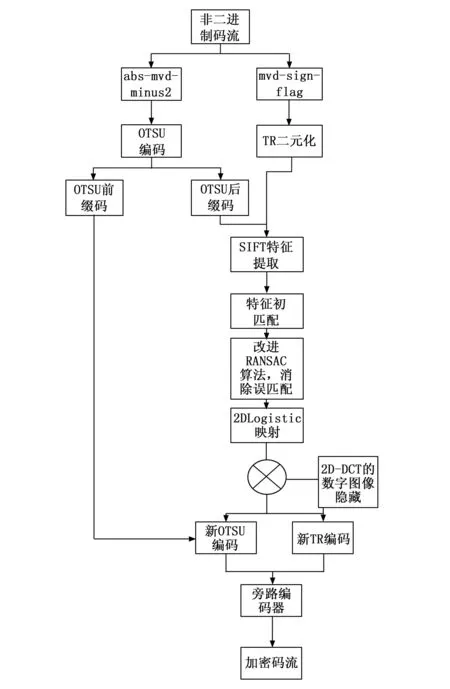
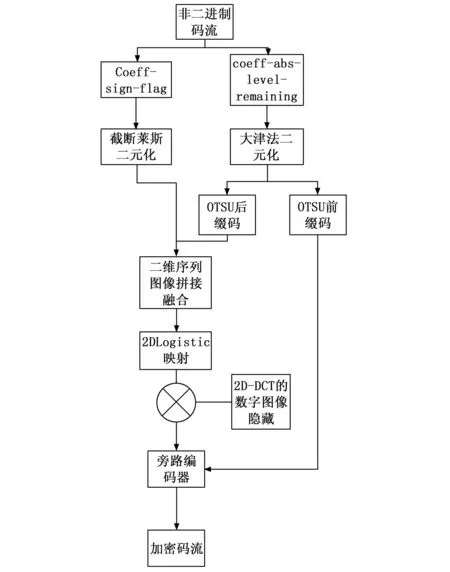
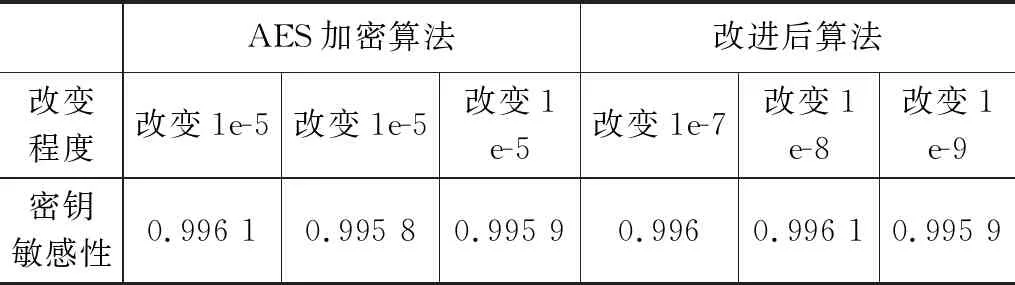
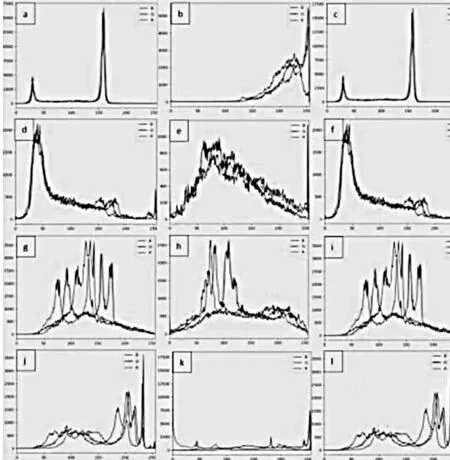
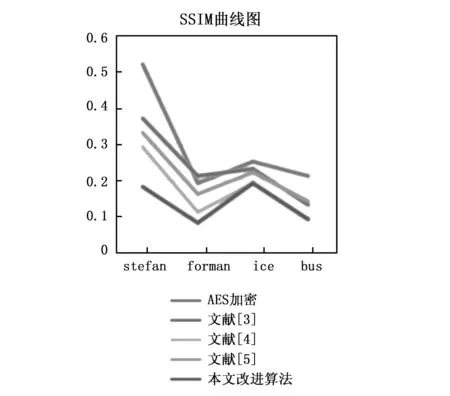
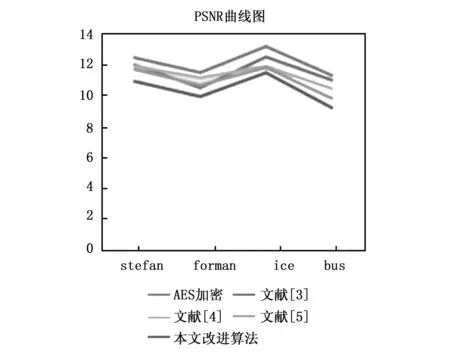
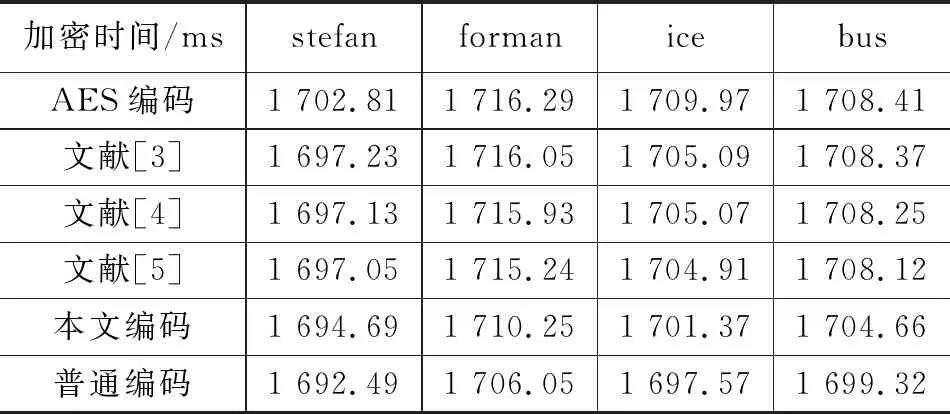
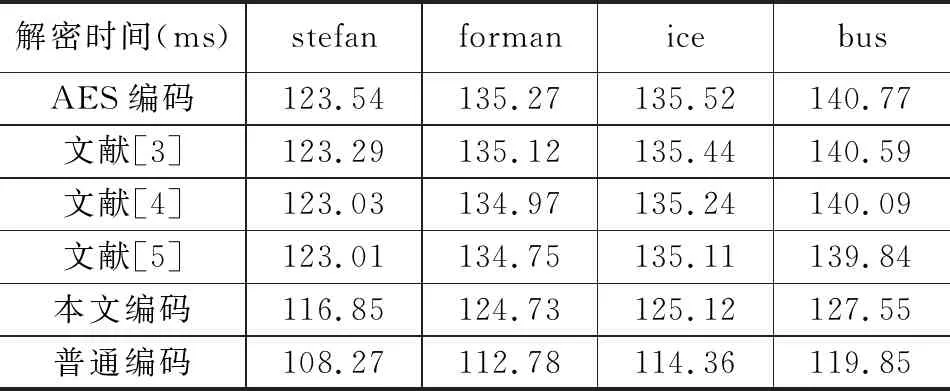
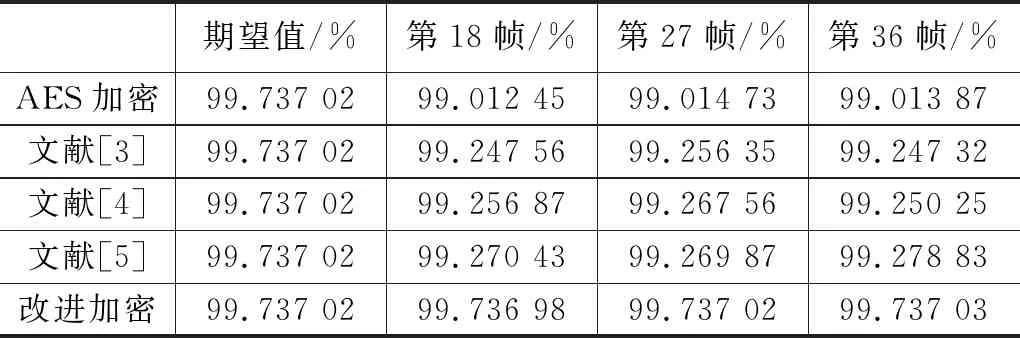
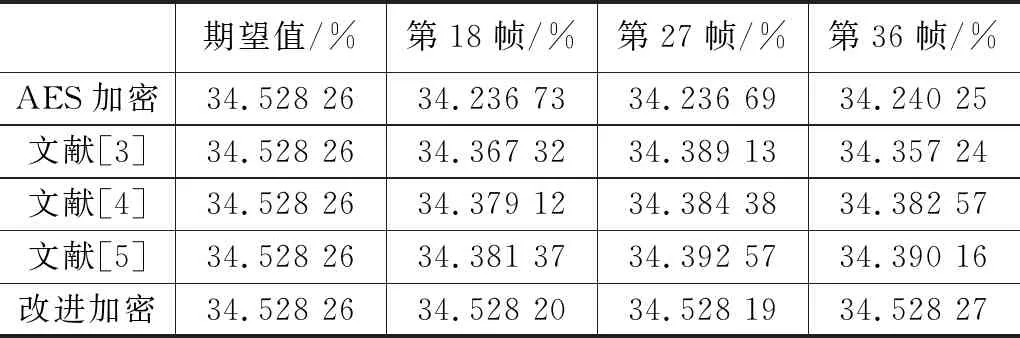
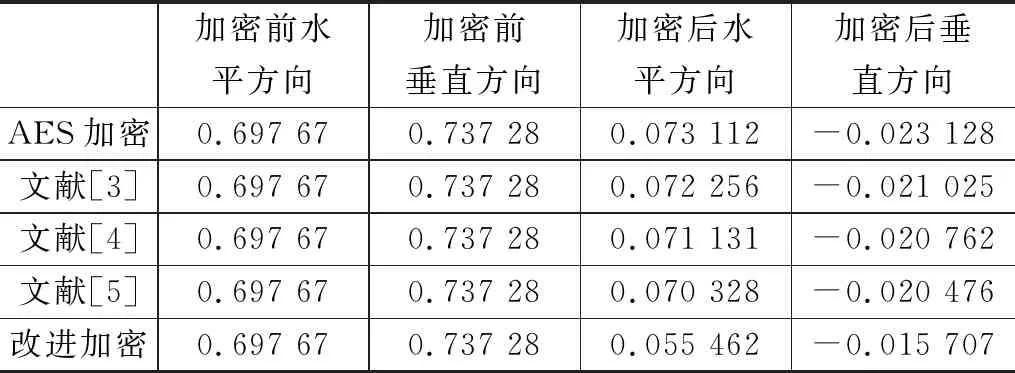
设p=k*i+r,(r (1) 则K*i+r=0(modp) (2) 两边同乘r-1+i-1,得 K*r-1+i-1=0(modp) (3) 移项,得 i-1=-k*r-1(modp) (4) 即 (5) 我们可以利用该公式进行递推,边界条件为1-1恒等于1(modp),时间复杂度为O(n)。 行移位是一个简单的左循环移位操作。当密钥长度为128比特时状态矩阵的第0行左移0个字节,第一行左移1字节,第二行左移2字节,第3行左移3字节,如图1所示。 图1 12行移位操作图 列混淆是在有限域下将状态的每列(a0a1a2a3)T的转置乘以一个固定多项式C(x)模乘4加1,多项式 C(x)=03*3+01*2+01*02 (6) 该变换以矩阵形式表示为: (7) 明显可知,列混淆中矩阵乘法较多,计算量较大,这里我们可以利用数学中矩阵乘法次数进行优化:对于矩阵的乘法运算是相乘再相加,所以执行的乘法次数就是Ai*Ak*Aj,第i个到第j个矩阵的乘法次数为: matrix[i][j]=matrix[k+1][j]+ d[i-1]*d[k]*d[j] (8) 根据运动矢量特性可以选取语法元素abs-mvd-minus2和mvd-sign-flag进行二值化,这两种元素分别是运动矢量残差幅值和运动矢量残差符号,残差数据可以体现相邻像素的相关性,对这两种元素采用不同的二值化方法。语法元素前者abs-mvd-minus2采用OTSU方法,该方法较大的一个优点便是不用考虑分块后的图像直方图是否具有明显的双峰;语法元素后者mvd-sign-flag采用截断莱斯二元化方法TR,其前缀是一元码,后缀是定长码,后缀长度为cRiceParam,但是注意最后有截断的情况输入参数为cRiceParm cMax以及要二值化的val。通过对AES编码标准[9]的语法元素进行筛选,可以得到如图2所示的适合本文加密的语法元素。 表1 适合加密的算法筛选 图2 运动矢量符号位加密 本文最大的创新即是在运动矢量加密以及DCT[10]变化系数加密时,在DCT变化系数二值化后,对运动矢量的残差数据进行二维序列处理时采用改进后的二维序列图像拼接融合技术,再结合2DLogistic映射与2D-DCT的数字图像隐藏技术,生成新的二值化编码。 二维序列图像拼接融合技术[11-13]包含数字图像拼接融合的基本流程、图像配准常用的算法、消除误匹配的算法、图像融合中常用的算法等,当然,采用SIFT特征初匹配算法很好地解决了畸形图像的拼接问题,通过改变校正算法和对图像进行SIFT特征提取、特征初匹配,利用RANSAN算法实现了误匹配的消除。 2DLogistic映射与2D-DCT的数字图像隐藏技术即是利用二维Logistic映射产生的混沌序列对秘密图像的像素进行扩散和置乱[14-15],达到了秘密图像的加密效果,然后分块对载体图像进行二维离散余弦变换,对扩散和置乱后的图像信息分存在变换后的每块右下角,最后进行二维离散余弦反变换,从而得到了隐藏图像。 运动矢量加密分析主要靠运动矢量的局部最优性和相邻相关性来构造特征。前者借助运动矢量残差来提取特征,后者借助运动矢量本身的相关性提取特征。运动矢量是可以用坐标系表示的,设运动矢量坐标系为MV(x,y),所作直角坐标系可以用肉眼进行直接分析,当改变运动矢量的横纵坐标的符号位,运动矢量的语法元素也随之发生了改变,运动矢量符号位加密如图3所示。 图3 运动矢量的加密流程图 Cosff-abs-level-remaining和Coeff-sign-flag语法元素是DCT变化系数加密所需要的语法元素。对DCT变化系数进行的二值化[16]最好的方法是采用对角线的处理模式,下图为改进算法的DCT视频加密流程如图4所示。 图4 DCT的视频加密流程图 对于视频加密技术而言,验证该加密技术效果是否良好最重要的几个参考角度便是视频质量、运算效率、密钥敏感性。因此,本文在Microsoft Vissual Studio 2017上搭建实验所需的集成开发环境,硬件平台为台式电脑,型号为i7-6700,主频为3,40 GHZ电脑运行内存为4 GB,系统为Windows7环境,对本文改进后的AES算法与AES算法两者的密钥敏感性作对比,判断本文改进后的AES算法的密钥敏感性是否比AES算法的密钥敏感性更加良好,从视频质量角度上对本文中改进后的AES算法加密前后的RGB直方图对比分析判断本文中改进后的AES算法加密质量和还原性能是否良好,从而判断本文中改进后的AES算法加密效果是否良好,从视频质量中的SSIM值以及PSNR值、加密算法运行效率两个方面分别对比原AES视频加密、文献[3]中改进算法、文献[4]中改进算法、文献[5]中改进算法、本文改进后的AES算法进行实验分析本文中改进后的AES算法加密是否具有优越性。下图为stefan、forman、gice、bus的原始帧及加密帧: 图5(a)为stefan原始帧,图5(b)为stefan加密帧,图5(c)为gice原始帧,图5(d)为gice加密帧,图5(e)为forman原始帧,图5(f)为forman加密帧,图5(g)为bus原始帧,图5(h)为bus加密帧。 图5 图像对比 密钥敏感性是指在加解密过程中,初始密钥发生微小的变化,经密钥序列发生器或迭代函数作用后所产生的密钥发生巨大变化,从而加解密图像发生巨大变化。密钥敏感性是密码系统是否安全的主要因素,如果在加解密过程中将图像的像素值设置为控制参数并作为初始密钥,那么该算法不仅仅具有密钥敏感性,而且可以抵抗已知明文攻击。分析密钥敏感度方法为:使用两个不同的密钥加密同一语法元素序列,然后比较加密结果。 表2 密钥敏感性对比 若密钥改变一位,则解密图像中像素值的像素个数占总像素个数的比例发生了变化,将理想结果0.996 1的定量计算数值进行引入来衡量密钥敏感性。算法中,初始密钥为[0,0,0,1e-5],在测试中,改变密钥的十万分之一,即1e-5,变为[0,0,1e-5,1e-10]对密文进行解密。为了更具普遍性,继续改变1e-7、1e-8、1e-9不同的初始密码,并与AES加密原本算法进行对比分析,实验多次改变初始密钥的结果都在0.996 1附近,相比单纯AES加密算法密钥敏感性,本文改进后的密钥敏感性更好,从而可以抵抗已知明文攻击。 RGB直方图[17]是图像检测系统中广泛采用的颜色特征,可以通过比较phthon语言输出的原始帧和解密帧的RGB直方图是否一致以及加密帧的RGB直方图来判断视频加密质量,下图分别为gice、bus、stefan、forman的原始帧、加密帧、解密帧的RGB直方图: 图6的图(a)为gice原始帧的RGB直方图,图6的图(b)为gice加密帧的RGB直方图,图6的图(c)为gice解密帧的RGB直方图,图6的图(d)为bus原始帧的RGB直方图,图6的图(e)为bus加密帧的RGB直方图,图6的图(f)为bus解密帧的RGB直方图,图6的图(g)为stefan原始帧的RGB直方图,图6的图(h)为stefan加密帧的RGB直方图,图6的图(i)为stefan解密帧的RGB直方图,图6的图(j)为forman原始帧的RGB直方图,图6的图(k)为forman加密帧的RGB直方图,图6的图(l)为forman解密帧的RGB直方图。 图6 直方图 显然,改进后算法的原始帧与解密帧基本一致,说明视频加密解密性能良好,加密帧图像的像元灰度值分布不具有概率统计分布的基本特征,即视频加密质量良好。 SSIM指数[18-20]通常用来评价视频相似度,如果SSIM值<0.6,则视为具有良好的保密性。计算公式如下所示: (9) C1=(k1L)2 (10) C2=(k2L)2(k=0.03) (11) 本文针对不同视频的100个I帧执行SSIM评估,AES算法、文献[3]、文献[4]、文献[5]、改进后的算法进行了分析对比,结果如图7所示。 图7 不同视频序列的SSIM测试结果图 图7中,五条曲线由上至下分别为AES加密序列帧、文献[3]序列特定帧、文献[4]序列特定帧、文献[5]序列特定帧、本文改进算法加密序列特定帧,经SSIM曲线图对比分析可知,相较而言,本文改进后的AES算法加密的SSIM值最小,其密文与明文之间的相似程度更小,即加密效果更好。 PSNR峰值信噪比[21-23]是评价视频加密前后对比的一项重要指标,PSNR指数越高,越不容易失真,PSNR值≥20为可接受范围内,如果大于30,则视频加密前后质量非常好。计算公式如下: (12) (13) 其中:MSE[24-25]为均方差,代表相邻像素点之间的相关性,V是原始像素点的行个数或者列个数,C是视频帧图像的加密图像,均方差值越小,峰值信噪比越好,则加密会有更好的效果体现。 图8中,五条曲线由上至下分别为AES加密序列帧、文献[3]序列特定帧、文献[4]序列特定帧、文献[5]序列特定帧、本文改进算法加密序列特定帧,由图明显可知,本文改进后加密序列特定帧PSNR值PSNR值相对更低,与AES加密序列特定帧PSNR值差距更大,即加密效果明显更好。 图8 不同序列的PSNR测试结果图 评价加密技术的一个关键特征就是处理时间[26-27]。计算机在每个测试时间所给出的执行不同,表3是计算了100个I帧对于AES加密与改进后加密由于加密过程而增加计算时间的速率对比。 表3 加密时间运算效率 表3中,从左到右分别为stefan、forman、ice、bus的AES加密编码、文献[3]编码、文献[4]编码、文献[5]编码、本文改进后的AES加密编码、普通视频编码的加密编码时间(ms)。 表4中,从左到右分别为stefan、forman、ice、bus的AES加密编码、文献[3]编码、文献[4]编码、文献[5]编码、本文改进后的AES加密编码、普通视频编码的解密编码时间(ms)。 表4 解密时间运算效率 表3中,将AES加密编码、文献[3]编码、文献[4]编码、文献[5]编码、本文改进后的AES加密编码分别与普通视频编码的作比较,经计算,AES视频编码加密时间增幅为0.65%,文献[3]视频编码加密时间增幅为0.46%,文献[4]视频编码加密时间增幅为0.456%,文献[5]视频编码加密时间增幅为0.44%,本文改进后的AES视频加密编码加密时间增幅为0.23%,从而可知本文改进后的AES视频加密的加密时间最少,即本文改进后的AES视频加密运算效率最好。 表4中,将AES加密编码、文献[3]编码、文献[4]编码、文献[5]编码、本文改进后的AES加密编码分别与普时间增幅为通视频编码的作比较,经计算,AES视频编码解密17.54%,文献[3]视频编码解密时间增幅为17.39%,文献[4]视频编码解密时间增幅为17.14%,文献[5]视频编码加密时间增幅为17.01%,本文改进后的AES视频加密编码解密时间增幅为8.56%,从而可知本文改进后的AES视频加密的解密时间最少,即本文改进后的AES视频加密运算效率最好。 3.4.1 密钥空间分析 密钥空间包含了运动矢量和DCT变化系数在加密过程中所有加密元素的全部可能性,密钥空间的大小与加密元素的种类和语法元素可能性的多少有直接关系,并且密钥空间与它们分别均为正相关的关系。密钥空间的计算公式如下: Sframe=(242l+12k+1)n=22WH/1024*2(l+4)m+(k+l)n (14) 其中:m和n为加密编码的编码块个数,视频分辨率为W*H,k为加密语法元素的后缀码长度,l为DCT变化系数的语法长度,预估计的密钥空间为24,在改进算法运动矢量的密钥空间为2k+1,改进算法DCT变化系数的密钥空间为2l+1,假定视频序列分辨率为496*448,则改进算法帧图像的密钥空间Sframe≥2256。一般地,密钥空间大于2100则认为足够抵抗穷举攻击,本文改进算法的密钥空间远大于2100,因此本文改进后算法视频加密抗攻击性十分良好。 3.4.2 抗差分攻击分析 加密中,像素改变率NPCR和统一平均变化强度UACI可以充分反映原始视频帧图像和加密后视频帧图像的关系,当攻击方对加密的原始视频帧图像进行细微的改变时,若视频帧图像发生了巨大的改变,则所受到的这种明文攻击将会失效。 (15) (16) 其中:CR,G,B为所加密的图像,M、N分别是该所加密图像像素的行数和列数。 表5和表6是某像素点改变时,AES加密、文献[3]、文献[4]、文献[5]、改进加密的视频帧分别受到的影响。经表中测试结果可知,改进加密视频帧所受影响后改变最为明显。因此,本文改进加密的抗差分攻击能力较强。 表5 NPCR测试表 表6 UACI测试表 3.4.3 抗统计攻击分析 加密后,视频帧图像都具有水平和垂直的相关性。相关性越大,代表视频加密效果越差;相关性越小,代表视频加密效果越好。 (17) (18) (19) (20) 其中:x、y为视频帧相邻像素灰度值,E(x)和D(x)为其数学期望和方差,rxy为其相关系数。 对AES加密、文献[3]加密、文献[4]加密、文献[5]加密、改进后加密下在水平和垂直方向加密前后像素对的相关系数分别进行测试。 由表7测试结果可知,改进后加密无论是在水平方向还是垂直方向加密前后像素对相关性明显最小,抗统计攻击性最强,即改进后视频加密效果最好。 表7 加密前后像素对的相关系数 本文在加密过程实现了算法创新,在加密元素的选取板块,由于二值化是处理异或运算比较好的一种方法,文中引入了相对更为合适的定长二进制的二值化方法,使得需要进行异或运算的轮密钥加得到了方法上的进一步优化;为了计算更加简便,通过比较求乘法逆的各种方法,在拥有大量乘法逆计算的字节代替环节进行了更优乘法逆方法的找寻;为了处理大量的矩阵乘法运算,利用数学中的矩阵乘法次数的优化使得处理列混淆上更加简便。通过对AES编码标准的语法元素进行筛选,得到了合适的加密语法元素,在DCT变换的图像压缩编码方法中,采用大津法和截断莱斯二元化分别对运动矢量和DCT的元素进行二值化。且在DCT的二维序列处理上引入了二维序列图像拼接融合技术,再结合2DLogistic映射与2D-DCT的数字图像隐藏技术。在后续仿真验证中,相比原本AES算法,密钥敏感性得到了很好的提升;视频质量方面,相比原本AES算法和文献[3-5],本文改进后的AES算法的RGB直方图可知其加密效果和解密还原效果良好,改进后的AES算法加密的SSIM值最小、PSNR值更低,即加密效果相对更好;运行效率经过计算可知,编码时间百分比增加了0.23%,解码时间百分比增加了8.56%,经过对比原本AES算法和文献[3-5],本文改进后的AES算法所需处理时间更短,抗统计攻击和抗差分攻击性能均最好,因此改进后视频加密效果相对更好。 在当今互联网高速发展的时代,视频加密技术有着非常大的发展潜力,非常值得进一步深入探索,尤其是对于国家网络安全、国家核心科技安全来说,视频加密技术显得极其重要,下一步将本文中改进后的AES算法尝试应用到工程应用中并与最新其他加密技术对比分析分别应用到工程后对工程所产生的价值。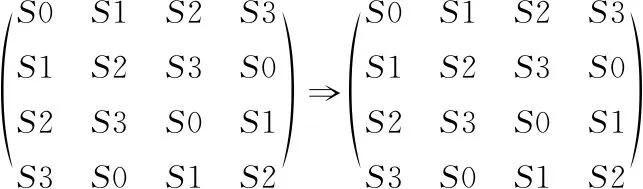
2.2 基于运动矢量的加密方案设计
2.3 基于DCT变化系数的加密方案设计
3 仿真结果及实验数据分析

3.1 密钥敏感性分析
3.2 视频质量分析
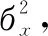
3.3 加密算法运行效率分析
3.4 改进加密算法安全性能分析
4 结束语

