基于有限元分析的橡胶回弹性模拟

雍占福，王茂辉，黄兆阁

（青岛科技大学 高分子科学与工程学院，山东 青岛 266042）

橡胶制品受到外力作用而发生高弹性形变时，橡胶分子的分子链构象和构象熵也会发生很大变化。 而小分子材料受力改变的是晶胞的尺寸（键长和键角），故其形变量很小，材料弹性变形很小［1-3］。 所以橡胶制品在外力作用下发生形变时，由于其分子链的变化，会导致分子链之间发生摩擦，造成能量的损失。 高分子材料回弹性的测定按照GB/T 1681—2009 （ISO 4662）硫化橡胶回弹性标准进行， 实验过程需要经历橡胶混炼、橡胶硫化及制作标准试样，最后才进行回弹性测试［4］。 本工作则提出了一种分析高分子材料回弹性以及回弹过程中能量变化的新方法，借助有限元分析软件ABAQUS 对橡胶的回弹性测试实验进行仿真模拟，探究橡胶在实验中理想状态（无摩擦、阻力等因素影响）下的能量损耗，并与实际回弹实验进行对比以确认方法的准确性［5］，借此获得橡胶真正的黏性损耗以及因为黏弹性造成的能量损失率。

机械式橡胶弹性测试仪回弹性的求法主要有2 种，一种是基于回弹高度的测定，另一种是基于回弹角度（α）的测定，其回弹性（R）的计算分别如式（1）和式（2）所示：

式中：hr为回弹高度；h0为摆锤下落高度。

1 有限元模型的建立

1.1 建立模型

对摆锤式橡胶机械回弹仪进行模型简化，忽略其试样夹持装置及机座等结构，建立简化后的仿真模型。 仿真模型主要由3 部分组成，分别是摆锤、冲头及试样。 将各部件按照正确位置装配到一起， 模型尺寸按照GB/T 1681—2009 规定执行，三维有限元模型如图1 所示。

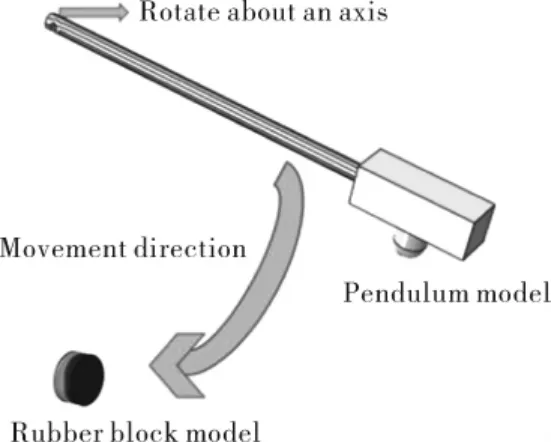
Fig 1 Diagram of three dimensional finite element model of rebound instrument

1.2 超弹性本构模型

选取合适的材料本构模型是保证有限元仿真分析准确性的关键因素之一，目前常用的表征橡胶材料的本构模型主要基于热力学统计方法和连续介质力学理论提出［5-6］。 在ABAQUS 软件中， 常用的橡胶复合材料本构模型有Mooney-Rivlin 模 型、Neo-Hookean 模型 和Yeoh 模型［7-9］。本研究在前人工作基础上，通过循环拉伸的方式消除了哑铃形试样的Mullins 效应， 选用单轴拉伸的测试方法得到了材料的应力应变曲线，将其导入ABAQUS 的property 模块进行超弹性材料参数的拟合，拟合曲线如图2 所示。 由图2 可以看出，Yeoh 模型拟合度最高， 所以本研究选用Yeoh 模型作为仿真所用材料属性。 实验采用GB/T 1681—2009 规定的哑铃形试样Ⅱ型，长20mm、厚2 mm，拉伸速率为500 mm/min。

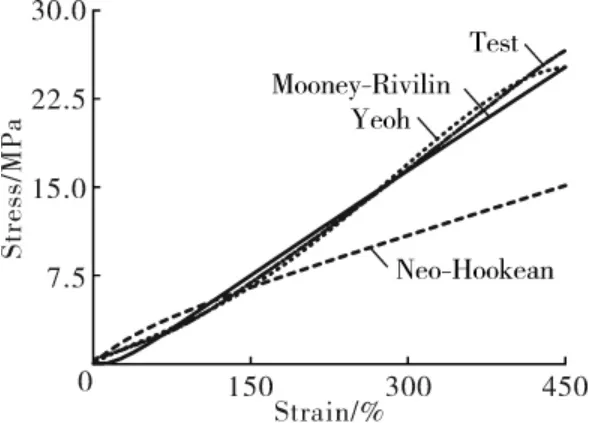
Fig 2 Stress-strain curves of vulcanized rubber under different models

1.3 黏弹性模型

橡胶高弹性来源于构象熵的变化，构象熵变化是由于高分子链链段的运动引起，链段的运动会造成分子链间及分子链与填料间的摩擦，导致滞后现象产生，引起能量变化。 因此，仿真中的黏弹性材料属性对动态分析结果至关重要［10-11］。 橡胶的黏弹性采用广义Maxwell 模型表示， 通过应力松弛实验确定参数，对应力松弛实验数据进行归一化处理，基于最小二乘法拟合出Prony 参数，以其作为材料黏弹性参数（见表1）［12-13］。 其中，G（i）为剪切模量，τ（i）为松弛时间。模型的应力松弛方程可用式（3）表示：

式中：σ（t）表示t 时刻的应力；σ0i和τ（i）分别为第i 个Maxwell 模型的初始应力和松弛时间。 由于其应变一定，则应力与模量正相关，即G（i）与初始应力σ0i正相关。

Table 1 Rubber material Prony parameters

黏弹性材料的损耗往往与温度、振动频率和应变幅度有关［14］，因此仿真过程中温度设定为实验室测试温度20 ℃，拟合材料属性选用的是接近仿真应变过程的100%应变条件下的应力松弛曲线。 图3 所示为实验与黏弹性模型拟合结果，由图3 可以发现， 天然橡胶试样的应力随时间减小，由于其应变一定，即剪切模量（G0）随时间的增加而逐渐减小，最终趋于稳定值。 此外，基于时间的上述应力松弛方程也可用剪切松弛函数方程g（t）表示：

式中：GR（t）为松弛时间t 时刻的剪切松弛模量；G∞为长时间下的剪切模量。 将剪切模量的Prony级数由时域转换为频域，式（4）可转换为关于阶数N 的式（5）：

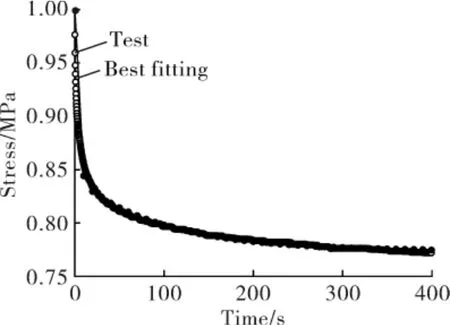
Fig 3 Stress relaxation curve under 100%strain condition

1.4 材料属性验证

合适的材料属性是影响仿真结果准确性的重要因素之一［15-17］。 为了验证拟合材料属性的准确程度，保证仿真数据的科学性和精确度，使用拟合后的材料属性进行橡胶单轴拉伸实验的仿真模拟，然后与实际拉伸实验对比，对应力进行平均处理，默认平均阈值是75%，结果见图4。 不同应变条件下试样的仿真结果与实际拉伸实验结果对比发现， 哑铃形试样仿真得到的应力-应变曲线与材料参数拟合得到的曲线基本重合，与实验测得的数据相近，证明以上讨论获取的材料参数能准确模拟回弹橡胶块的力学特性，可以用于回弹实验有限元模型的建立。 其保证了实验中材料属性的准确性，同时也可为之后的能量分析提供佐证。

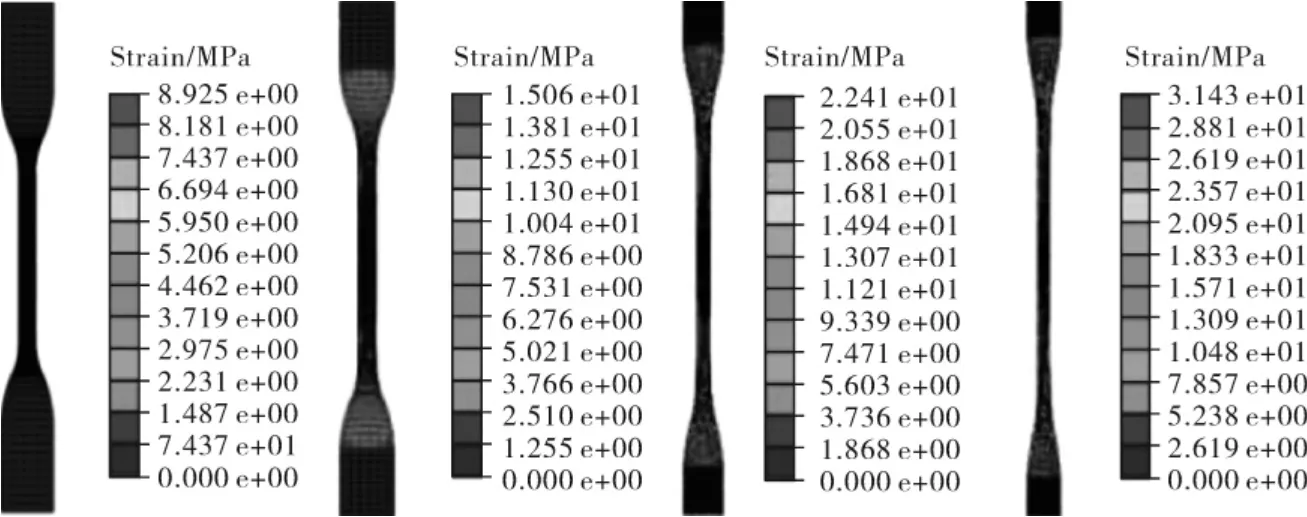
Fig 4 Simulation and actual comparison of rebound sample under different strains

2 结果与讨论

通过实际测试和本方法模拟可知，实验测试的橡胶回弹角度为64°09′时，仿真模拟为66°54′，误差为3.8%； 实验测试的橡胶回弹率为59.4%时，仿真模拟为60.8%，误差为2.4%。由于有限元分析是在理想条件下进行的，所以忽略了实际测试时的空气阻力和摩擦造成的能量损失，导致仿真模拟结果从数据上要略微高于实验测试结果。回弹率的精确程度较高也可以证明回弹过程中能量变化的准确性。

2.1 能量变化

在回弹实验中，从摆锤释放开始，其重力势能转化为动能且逐渐增大，当摆锤降落到最低点时的动能最大；摆锤撞击到高分子试样，高分子链变为伸展状态，无序性和构象熵减少。 此后伸展状态的分子链变为无规卷曲状态， 构象熵增加，反作用于摆锤，使摆锤回弹，根据回弹高度或回弹角度确定材料的回弹率［4］。 实验过程中最直观的表现是摆锤无法回弹至初始位置，其冲击试样的过程中存在能量损耗，这部分损耗是高分子材料的黏弹性引起［18］。 本方法测定的回弹率与实际结果相符，因此对实验过程中用有限元方法分析能量的变化也应是准确的。 图5 为试样回弹过程中能量的变化曲线，可以看出，摆锤大约在释放后0.27 s 能量达到最大值， 冲击试样后能量迅速降低，然后迅速达到回弹的最高值，但是显然该值无法达到冲击前的能量大小；模拟的能量是试样中储存的能量和摆锤动能之和，因为试样在摆锤离开后会迅速回弹至原来的形状并围绕该形状周期振动，因此试样中储存的能量呈现上下波动并逐渐降低。

Fig 5 Energy change curves of sample during rebound

图6 为回弹过程中试样中储存的摆锤动能与应变能的关系曲线， 可以看出， 摆锤大约在0.27 s 时冲击试样，将摆锤的动能传递给试样，试样在0.27 s 时储存的摆锤动量最大； 当摆锤回弹时，试样将一部分能量返还给摆锤成为摆锤的动能，另一部分能量成为试样的应变能。 从图中可以发现两种能量的变化相同，都呈现周期性上下波动并逐渐递减的规律； 不同的是二者峰值相反，即试样中储存的摆锤动能处于最大时，试样的应变能处于最小，二者彼此交替循环，试样中储存的部分摆锤动能先变化，试样应变能的变化相对滞后，其特点正反映出高分子材料的滞后现象，而试样中能量的损耗也正是因为这种滞后现象的存在［19］。

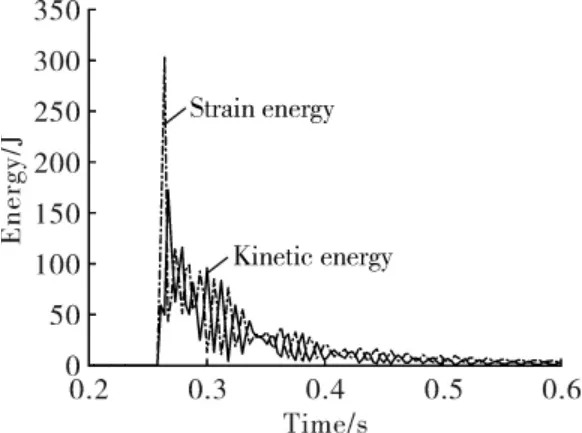
Fig 6 Relationship change curves of kinetic energy and strain energy of sample during rebound

综合图5 和图6 可以发现，摆锤冲击后的动能大部分通过接触传递给试样，试样形变到最大后又反作用于摆锤使其回弹，同时一部分能量变成试样的应变能。 摆锤离开试样后，试样残余的能量与应变能相互交替，微观上表现为分子链在无规则卷曲和伸展状态之间不断变化，链段之间彼此摩擦，能量逐渐被消耗并最终趋于稳定。

2.2 温度变化

高分子材料中分子链被迫由无规卷曲状态变为伸展状态，无序性和构象熵减少，然后自发地从伸展状态变成另一种无规状态［19］。 在转化过程中，分子链间必然伴有链段间及分子链与填料间的摩擦，导致机械能转化为热能，使温度升高。图7 为试样在不同冲击时间的温度变化（环境温度20 ℃），从中可以发现，初始冲击时试样温度最高，撞击的瞬间0.27 s 时试样最高温度达到46.34℃，温度范围很小，这是因为冲击时应变最大，外力作用快，分子链之间的摩擦更强烈。 随着时间的延长，最高温度趋近于环境温度20 ℃，热量从试样中间位置向周围传递，高于环境温度的范围越来越广，最终以热能形式散失到环境中。

Fig 7 Simulated temperature distribution of rebound sample at different impact time

试样温度场的变化除了高分子材料滞后现象的原因外，还因为撞击过程中摆锤与试样相对运动而产生的摩擦［3］。 因为摆锤冲击试样时存在接触，接触后试样发生形变，在动摩擦系数为0.2的条件下会发生摩擦。 图8 为摆锤作用时试样的摩擦力分布情况， 将输出的应力与试样直径作图， 更直观地分析试样在撞击过程中的受力情况。 从图8 可以发现，中心点处由于冲头沿垂直方向冲击试样表面，此处几乎没有摩擦力，而中心点周围接触应力更大， 在距离中心点5 mm 左右处产生的相对滑移更大，因此摩擦力最大。 从图9 可以看出， 由摩擦力引起的能量耗散（ALLFD）也是回弹过程中能量损耗的一部分，只是这部分占比很小。

Fig 8 Simulated friction distribution of rebound sample during pendulum action

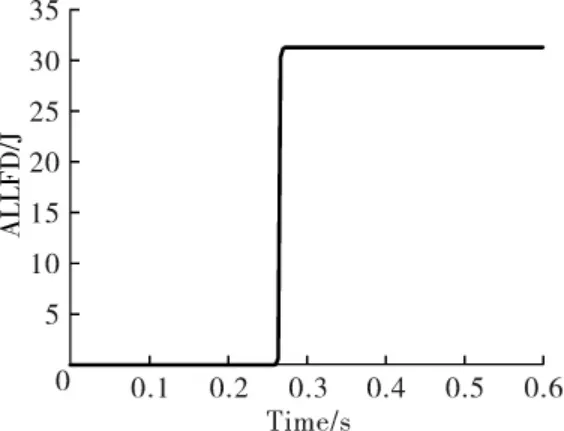
Fig 9 Energy dissipation curve of rebound sample

3 结 论

提出了基于有限元分析的橡胶回弹性模拟新方法，实验测定结果显示该方法模拟计算结果与其相符，对于橡胶材料回弹角度和回弹率的模拟精确度达到96%以上，这与黏弹性模拟计算考虑了WLF 方程的影响有关， 可以更好地模拟高分子材料的生热现象。