量子噪声对Shor 算法的影响

黄天龙 吴永政 倪明 汪士 叶永金

(中国电子科技集团公司第三十二研究所,上海 201808)

Shor 算法能够借助量子计算机以多项式级别复杂度解决大整数因式分解问题,从而破解一系列安全性基于大整数因式分解的加密算法,例如Rivest-Shamir-Adleman 加密算法、Diffie-Hellman 密钥交换协议等.由于量子测量结果是概率性的,在运行量子线路时很容易受到噪声的干扰,这将导致无法测量得到预期结果.本文分别研究了不同通道的噪声对Shor 算法的影响,分别是去极化通道、状态制备与测量通道以及热退相干通道.本文模拟在噪声环境中运行Shor 算法并且给出了数值结果.数值结果表明Shor 算法成功分解整数的概率易受到噪声影响,其中去极化通道中的噪声能够以指数形式影响Shor 算法成功分解整数的概率,其次是热退相干通道噪声,最后是状态制备与测量通道噪声,能够线性影响到Shor 算法成功分解的概率.本文能够为后续纠错、改进Shor 算法以及确定工程实现Shor 算法所需要的保真度等提供建设性意见.

1 引言

Shor[1]于1994 年提出用于解决大整数因式分解的量子算法,该算法能够以多项式级的复杂度解决大整数因式分解及离散对数问题[1,2].相较于经典因式分解算法,Shor 算法有指数级提升.目前复杂度最低的传统大整数分解算法是数域筛法[3-5],它的复杂度为Kleinjung等[6]借助上百台计算机花费两年时间使用数域筛法分解了一个768 比特的RSA (Rivest-Shamir-Adleman)整数,并且指出分解2048 比特的RSA 整数的开销是前者的百万倍.而文献[7]指出理论上在一台拥有两千万个物理比特的量子计算机上运行Shor 算法可以在8 h 内完成2048 比特的RSA 整数的分解.然而目前的量子计算机系统仍然处于萌芽状态,我们处于带噪声的中等规模的量子计算机时代(noise intermediate-scale quantum,NISQ)[8].中等规模指的是量子计算机所含有的量子比特个数范围为50—100,并且量子计算机运行量子算法时会受到噪声的影响.噪声是搭建NISQ 时代量子计算机的主要障碍[9,10].噪声出现的主要原因在于硬件(酉门)的失真以及量子计算机与环境之间会产生交互(例如弛豫与退相位、电磁退相干、引力退相干等)[11-13],这些噪声会对算法结果产生影响,导致与预期结果产生偏差.因此研究噪声对Shor 算法的影响是十分重要的.本文分别针对不同通道的噪声对Shor 算法的影响进行深入研究,通过数值分析任一通道中不同噪声大小与Shor 算法分解整数成功率的关系(Shor 算法成功率定义见2.2 节).

Shor 算法中的量子线路十分复杂,因此大量关于优化线路的文献被提出.Vedral等[14]首先搭建了算术运算的量子线路,其中包括加法门、乘法门以及模指数门等.模指数门是构成Shor 算法量子线路的重要组成部分.使用Vedral 等的方法搭建Shor 算法所需的量子线路需要7n+2 个逻辑比特,其中n是待分解整数N的二进制比特数.在此基础上Draper[15]改进了加法门.改进后的加法器需要两个输入a,b.与一般加法器不同的是,Draper加法门首先计算a的量子傅里叶(quatnum fourier transform,QFT)结果,记作F(a),紧接着再计算F(a+b),能够将Shor 算法中需要的逻辑比特数量级降低至2n.Beauregard[16]使用量子QFT 加法器以及半经典QFT (semi-classical QFT)构建Shor 算法线路.如果只使用一个量子比特循环控制受控模指数门,分解大整数N只需要2n+3 个逻辑比特.

由于真实量子计算机中噪声的存在,在不纠错的情况下运行复杂量子线路很难得到正确结果.关于在真实量子计算机上运行Shor 算法(使用纠错算法后)的开销也被分析.Fowler等[17]指出,以表面码为基础,当量子门噪声大小为10-3时,需要在一台拥有 2.2×108个物理比特的量子计算机上运行26.7 h,才能够分解一个2000 比特的整数.在O’Gorman 和Campbell[18]的工作中,使用了改进后的表面码,每个逻辑比特需要的物理比特数目更少,在量子门噪声大小为10-4的情况下,整个线路只需要 6.3×106个物理比特.Hwang等[19]在使用Steane 码以及表面码的基础上,对Shor 算法进行了分析,相比于文献[17,18]的工作,他们对Shor算法的分析更加详细,从而取得了更合理的结果,他们指出在量子门噪声大小为10-3的情况下使用Shor 算法分解一个512 比特的整数需要9.5×1010个物理比特并且花费 8.78×105h.Ha等[20]在使用旋转平面表面码[21]的基础上给出了待分解整数的比特数与分解时间以及分解所需要的量子比特数目的具体关系,他们指出,在量子门噪声大小为10-3的情况下分解2048 比特的RSA 整数需要1.37×107个物理比特,并且要花费 1.89×107h 完成.在Gidney[7]的工作中,他指出为了分解一个2048 比特的整数,在量子门噪声大小为10-3的情况下需要在一台拥有 2×107个物理比特的量子计算机上运行大约8 h.此外,Gidney[22]将窗口法与量子线路融合,进行量子运算的加窗操作,能够降低模乘法门中的线路深度.Xiao等[23]提出以量子隐形传态为基础使用两台量子计算机实现分布式的Shor 算法,能够降低每台量子计算机运行所需要的量子比特数目以及线路深度.Rossi等[24]提出了Shor 算法的简化版本,并且在IBM 的真实量子计算机上进行了验证,结果表明在损失部分准确率的情况下仍能够得到正确的分解结果.

然而鲜有强调关于给噪声建模或者模拟噪声对算法影响的文献[9,25,26].文献[10,25]提及了噪声建模的重要意义并且建立了对应的噪声模型.文献[27]研究了特定噪声对量子近似优化算法[28]的影响并且进行了数值分析.大部分实验室并没有可以运行的量子计算机,而一些公用量子计算机的比特数量以及相应参数不同,因此很难准确地进行量子噪声建模[29].根据文献[10],本文将噪声分成3 个通道分别进行研究,分别是去极化通道(depolarizing channel,DC)[30-32];状态制备与测量通道(state preparation and measurement channel,SPAM)[33];热退相干通道(thermal relaxation channel,TRC)[13,30].

目前Shor 算法中的量子线路的复杂度仍然很高.本文搭建的量子线路的深度达到了O(n3),线路宽度达到了4n+2.因此线路可能很容易受到噪声影响.一方面,明确量子计算机中噪声来源能够更有效地进行纠错[34,35];另一方面,了解不同噪声对Shor 算法的影响程度对于纠错也是十分重要的.本文针对噪声对Shor 算法的影响进行研究,根据文献[10]将噪声分成3 个通道,通过一系列模拟得到了每个通道中不同大小的噪声与Shor 算法成功率的数值关系,对于后续对Shor 算法进行纠错、改进等能够提供建设性的意见.

本文第1 节介绍Shor 算法以及量子噪声对Shor 算法的影响,分析本项研究的创新性以及意义;第2 节对Shor 算法进行系统梳理,定义了Shor 算法整数分解的成功率和均方误差并且分析了量子线路的复杂度;第3 节讨论3 个通道中噪声的模型以及作用过程;第4 节详述模拟噪声的实验过程并且对数值结果进行分析;第5 节总结数值模拟结果并且提出未来研究方向.

2 Shor 算法

Shor 算法将因数分解问题转换至一个求a在乘法群中的阶的问题[1].a的阶r=ord(a,N)的定义是能够使ar≡1(modN) 成立的最小的正整数r.算法流程如表1 所列.

表1 Shor 算法流程Table 1.Pseudo of Shor’s algorithm.

Shor 分解算法包括经典部分与量子部分.量子噪声会直接影响到其中的量子线路运行的结果.本节对Shor 算法量子部分进行系统梳理.

2.1 Shor 算法量子线路

Shor 算法的量子线路(量子求阶程序)如图1所示.

图1 Shor 算法中的量子线路Fig.1.Quantum circuit of Shor’s algorithm.

线路需要两个量子寄存器,分别含有t=个量子比特.对第一个寄存器中的每个比特施加一个H门得到均匀叠加态.并且第二个寄存器的初态为 |1〉.那么|ψ1〉=其中j=2t.Va量子门是通过量子线路实现的模指数运算,本质上是一个受控酉门[30],其定义为根据相位反冲原理,如果对第二个寄存器进行测量,将测量结果记作ab,其中 0 ≤b＜r.|ψ2〉将坍缩 至所有 |l〉的叠加,l满足al≡abmodN,即al与ab同余,并且l=kr+b,其中 0 ≤k＜r.那么|ψ3〉=其中c=.此时使用量子傅里叶逆变换[36-38]提取隐藏在第一个寄存器中的周期信息.根据量子傅里叶变换的定义可以得到:

其中ω=exp(2πi/j) .该态的含义是包含两种情况,分别是j|lr以及j∤lr的不同情况的叠加态.测量0 ≤l＜j的概率大小是:

当j能够被(lr)整除时,概率大小是c/j,此时对应的测量结果l满足l=kj,其中k是正整数.当j不能被(lr)整除时,P(l)会在l满足sin2(πlr/j)≈0的条件下产生极大值,对应的测量结果l应该满足l≈kj/r.因此对 |ψ4〉进行测量时,会有更高的概率使测量结果l满足l≈kj/r(约等于符号是因为测量得到的l是整数,是离散的)[39].

假设待分解的整数N=21,随机数选择a=2,那么r=ord21(2)=6,t==10,j=2t=1024,c==171,l的范围是0 ≤l＜1024,l∈Z.l的理论概率分布如图2 所示.

图2 Shor 算法分解(N=21,a=2)实验中 |ψ4〉 的预期概率分布Fig.2.Expected probability distribution of |ψ4〉 in factoring (N=21,a=2).

当l=0 或者l=512 时满足l|(qr),对应于图2 中最高的两个峰,其大小等于 1/r≈0.167 .其他情况(l≠0,l≠512 )下,当l≈k(j/r),即l=171,341,683,853 时,在图像中对应第二高的峰,大小约为0.114.|ψ4〉分布是有规律的.选择不同的随机数分解同一个整数时,分布会因随机数阶的不同发生差异.并且随着待分解整数增大,峰值概率也会降低.对于不同大小噪声下的情况,可以比较分布的差异从而判断出噪声对于线路影响程度的不同.

2.2 成功率的定义

在经典计算机上模拟时,能够计算 |ψ4〉的状态向量,因此能够得到l的分布.如果测量结果满足l=k(j/r),1≤k＜r,则可以进一步求其连分数[1](具体实现在附录A 中)最终完成对N的分解.例如在分解N=21(a=2)的实验中,|ψ4〉的概率分布如图2 所示,除去l=0,l=512,该分布有4 个峰值,将该4 个峰值的测量概率求和作为Shor 算法整数分解的成功率,即Ps=P(171)+P(341)+P(683)+P(853).对于一般情况,成功率的定义则是:

此外,本文还将均方误差(mean squared error,MSE)这一指标用于实验结果的比较,该指标定义式为

其中,P(l)theory代表l的理论概率分布,P(l)j代表某一噪声环境下第j次实验中l的概率分布,一共重复实验k次.而(P(l)theory-P(l)j)2的定义是所有可能测量得到的结果的理论概率与实际概率作差并求其平方和.这一指标能够很好地反映 |ψ4〉在不同噪声环境下的分布与理论分布的差异,从而能够帮助我们判断分解是否成功.

2.3 量子线路复杂度分析

本文以Draper[15]提出的QFT 加法器作为量子线路的算术基础,并且按照Beauregard[16]的方法依次搭建了模N加法门、受控模N乘法门、受控模指数门.与Beauregard 的方法不同的是,本文并没有使用半经典QFT,而是一般QFT (normal QFT),因此共需要4n+2 个量子比特.

QFT 加法门的深度为1,需要n+1 个量子比特,其中n是待分解整数N的二进制比特数.额外的一个量子比特用于防止溢出.模N加法门的复杂度取决于QFT 的精度.如果使用精确QFT,那么量子门数量为O(n2),线路深度达到了O(n),一共使用n+4 个量子比特,其中n+1 个比特用于实现QFT 加法门;2 个用于控制比特;1 个作为辅助比特.受控模N乘法门需要2 次QFT 以及n个模N加法门,线路深度达到了O(n2),共需要2n+3 个量子比特,其中n+2 个量子比特用于模N加法,另外n个比特用于存放 |x〉,剩下一个量子比特用于控制比特.受控模N指数门由一个受控模N加法门、受控交换门以及一个受控模N乘法门的逆门构成,因此深度仍然是O(n2),并且所需要的量子比特数目和受控模N乘法门相同,均为2n+3 个量子比特.搭建图1 中的Va门需要2n个Ua门,每个Ua门由不同的量子比特控制.最终的线路宽度为4n+2,线路的总深度达到了O(n3).

Shor 算法中的量子线路首先对第一个寄存器的所有的比特施加1个H门,并且在对第一个寄存器进行测量前进行1 次QFT 逆运算,分别需要O(n)个单比特门以及O(n2) 个双比特门.在QFT加法器中,需要1 次QFT 以及n(n+1)/2 个双比特门,那么单比特门的数量为O(n),双比特门的数量为O(n2) .在模N加法门中,需要3 个受控加法门、2 个加法门以及4 次QFT (其中2 次是逆变换)和2个X门以及2个CX门.那么双比特门的数量仍是O(n2),单比特门的数量为O(n).受控模N乘法门需要n个模N加法门以及2 次QFT (其中1 次是逆运算),因此该门共需要O(n3) 个双比特门以及O(n2) 个单比特门.Ua门包含 一个受 控模N乘法门、一个CSWAP 门以及一个受控模N乘法门的逆,不会改变所需量子门数目的量级.整个Shor 算法中共需要2n个Ua门来完成模指数运算.因此整个Shor 量子线路中共使用了O(n4)个双比特门以及O(n3) 个单比特门.

3 量子噪声

在量子计算机上运行量子算法的过程中噪声是不可避免的.噪声是构建大型量子计算机的主要障碍[9,10].随着构成量子线路的门数量增多以及使用的量子比特数增多,线路更容易受到噪声的影响,从而导致最终结果与预期产生偏差.根据2.3 节中的分析,Shor 算法中量子线路的宽度达到了4n+2,量子门数量达到了O(n4),在量子计算机上运行时很容易受到噪声影响,从而影响Shor 算法的成功率.因此模拟噪声环境中运行Shor 算法能够研究得到哪种噪声对算法的影响最大,能够使得纠错环节更加高效[34].本文根据文献[10]将噪声分为3 个通道进行研究,分别是去极化通道;状态制备与测量通道;热退相干通道.这3 个通道的噪声能够涵盖真实量子计算机环境中常见的噪声类别.

3.1 去极化通道

由于量子门的保真度无法达到100%,因此量子比特在经过量子门时会有一定的概率产生相位翻转或者比特翻转或者同时发生[30,40].比特翻转相当于在原有量子门基础上添加了一个X门.而相位翻转相当于在原有量子门基础上添加了一个Z门.当相位翻转和比特翻转同时发生时,相当于在原有量子门基础上添加了一个Y门.3 种泡利噪声出现的可能性相等.去极化通道作用于量子线路如下:

3.2 状态制备与测量通道

SPAM 通道的噪声仅导致状态制备后以及测量前的比特翻转.将SPAM 通道与DC 区别的原因在于,状态制备会向量子寄存器中注入预期的初态,会需要进行额外的操作,后者主要是发生在量子线路的运行过程中[33].将此通道中发生比特翻转的大小记作Pspam.使用算符和表达则是:

3.3 热退相干通道

退相干指的是量子比特与环境耦合过程中逐渐失去相干性的过程,来源于噪声与量子比特的微弱耦合[30,41].实际的量子比特系统很难做到完全孤立,除此之外,还要对量子比特进行测量,这就会使得量子比特总会与外部环境耦合.按照对量子比特的影响不同可以分为退相位(dephasing)[30]、弛豫(relaxation)[42].

3.3.1 退相位

3.3.2 弛豫

当T1越大时,该量子比特能够保持 |1〉状态的时间也越久.将纯退相位的过程一起考虑进来.根据(8)式,当能量弛豫与纯退相位两种噪声同时作用时,有

这里引入了参数T2来描述弛豫与纯退相位共同作用的结果,T2也被称为退相位时间.在实验中使用T1与T2来描述热退相干[25]噪声.T2与T1的关系为在模拟时,T2最大能够取到 2T1.在量子线路运行时(不包括测量与状态制备)每个量子比特经过量子门(单比特门、双比特门)都会按照(9)式同时发生弛豫与纯退相位.并且本文假定所有比特的热退相干模型相同,即共享一组T1,T2参数.

4 数值模拟

本文以Python 作为开发语言,借助用于量子计算的Qiskit库[44]进行模拟实验,在此基础上搭建了Shor 算法的量子线路、设置了不同的噪声环境以及计算 |ψ4〉的状态向量,从而计算 |ψ4〉的概率分布,并且按照2.2 节中的定义能够计算出成功率.这样做的优点在于仅进行一次模拟就可以得到准确的概率分布以及成功率,避免了通过重复测量得到分布的繁琐.按照第3 节将噪声分成3 类进行单独模拟.对于每一种噪声分别设置了不同参数区间,在不同噪声大小的基础上模拟运行Shor 算法量子线路,并且记录 |ψ4〉的分布.对于每次模拟,都至少重复1000 次,从而减弱随机误差的影响,将每次计算得到的成功率进行平均,作为最后的成功率,并进行进一步的分析.

4.1 去极化通道

本文针对去极化通道分别研究了单比特门去极化噪声与双比特门去极化噪声对Shor 算法的影响,并且认为所有的单比特门(X门,H门等)所经历的噪声大小相同.在运行量子线路过程中(不包括状态制备以及测量)当量子比特经过任意单比特门后,可能会发生X门翻转或者Y门翻转或者Z门翻转,概率均为P1/3 .本实验模拟了N=15,N=21,N=35 的分解,对于每个整数使用不同的随机数进行分解,具体组合如表2 所列.一次模拟整数分解实验所消耗的资源随着待分解整数比特增加而指数上升,代码运行时间只与待分解大整数的比特数目与硬件配置有关.平均1 s 左右即可完成一次对N=15 的分解.一次N=21 的分解实验需要消耗约12 s.而在对N=35 进行分解时,每进行一次分解实验需要花费大约2 min 的时间.对于每一次模拟都重复1000 次从而减弱随机误差,因此共需要花费约1.4 d 的时间完成,这导致无法对更大的整数进行模拟分解.

表2 实验选择的待分解整数与随机数组合(N,a)Table 2.Combination of integer about to be factored and random number (N,a).

对于每一个(N,a)组合,本文模拟了不同大小的单比特门去极化噪声作用于量子线路的实验.单比特去极化噪声大小取值为[0,0.0005,0.001,0.0015,···,0.01].对于双比特门去极化噪声,只有当目标比特经过任意双比特门(如CY门,CZ门,CX门等)后会发生X翻转或Y翻转或Z翻转,3 种噪声发生的概率均为P2/3,而控制比特不会受到影响.本文选择表2 的大整数、随机数组合进行模拟,对于每一个组合都模拟了其在不同噪声大小下的实验.P2取值为[0,0.00015,0.0003,0.00045,···,0.003].在去极化通道的模拟实验中,首先对比不同大小的单比特门去极化噪声对|ψ4〉的影响,如图3 所示.

图3 去极化通道中单比特门噪声对(N=15,a=2),(N=21,a=2),(N=35,a=2)中 |ψ4〉 概率分布的影响Fig.3.Effect of one-qubit gate noise in DC on probability distribution of |ψ4〉 in (N=15,a=2),(N=21,a=2),(N=35,a=2).

每一列子图都代表一组(N,a)组合,从左至右依次是N=15,N=21,N=35,每一组都选择a=2 作为随机数.每条曲线的数据都是1000 次模拟的平均并且归一化处理后的结果.|ψ4〉的分布随着噪声大小增大而变得更混乱.随着噪声逐渐增大,峰值大小相比无噪声时下降了很多.在3 组整数分解中,分解N=35 的实验受噪声影响最大.不同大小的双比特门去极化噪声对 |ψ4〉的影响如图4 所示.

图4 去极化通道中双比特门噪声对(N=15,a=2),(N=21,a=2),(N=35,a=2)中 |ψ4〉 概率分布的影响Fig.4.Effect of two-qubit gate noise in DC on probability distribution of |ψ4〉 in (N=15,a=2),(N=21,a=2),(N=35,a=2).

类似于图3,随着双比特门去极化噪声增大,每一组的分布更加混乱,峰值大小逐渐降低,分解N=35 受到噪声影响最大.按照2.2 节中定义的Shor 分解算法的成功率,给出了Ps和MSE 分别与两种去极化噪声的关系,如图5(a)和图5(b)所示(这里只给出部分结果,所有结果见附录B).

图5 (a) Ps 与去极化通道中单比特门噪声的关系;(b) Ps 与去极化通道中双比特门噪声的关系;(c) Ps 与状态 制备与测量 通道中噪声的关系Fig.5.(a) Effect of one-qubit gate noise in DC on Ps ;(b) effect of two-qubit gate noise in DC on Ps ;(c) effect of noise in SPAM channel on Ps .

图5(a)和图5(b)中的每个点对应相应噪声大小下成功率的具体值,曲线是对成功率与噪声大小关系的拟合,每组实验都选择随机数a=2.去极化噪声大小对成功率的影响呈指数形式,2.3 节中分析了量子门数量与待分解整数的二进制比特数的关系.随着待分解整数比特数目增多,线路中的门数量更多,导致成功率随着噪声增大而下降更快.成功率随着双比特去极化噪声增大而降低的趋势快于单比特门,原因在于线路中双比特门的数量多于单比特门数目.图6(a)和图6(b)是MSE 与两种去极化噪声的关系.

图6 (a) MSE 与去极化通道中单比特门噪声的关系;(b) MSE 与去极化通道中双比特门噪声的关系;(c) MSE 与状态制备与测量通道中噪声的关系Fig.6.(a) Effect of one-qubit gate noise in DC on MSE;(b) effect of two-qubit gate noise in DC on MSE;(c) effect of noise in SPAM channel on MSE.

4.2 状态制备与测量通道

在状态制备与测量过程中,本文假定所有制备状态或者测量的量子比特都会按照Pspam的概率发生比特翻转,选择表2 中的大整数、随机数的组合进行模拟.Pspam的范围是 [0.01,0.02,0.03,···,0.2] .类似于去极化通道,对于每一次模拟都重复1000次.首先对比不同大小的SPAM噪声对 |ψ4〉的影响,如图7 所示.

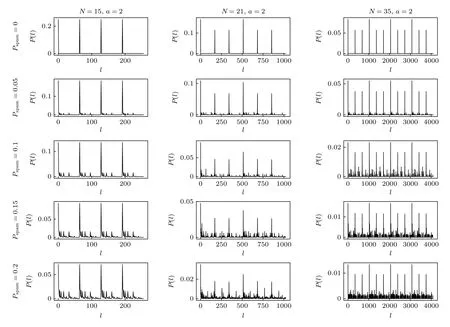
图7 状态制备与测量通道中噪声对(N=15,a=2),(N=21,a=2),(N=35,a=2)中 |ψ4〉 概率分布的影响Fig.7.Effect of noise in SPAM channel on probability distribution of |ψ4〉 in (N=15 a=2),(N=21,a=2) and (N=35,a=2).

在分解N=15 中,随着噪声增大,概率分布的峰值降低.|ψ4〉的分布相较无噪声情况更混乱.本文使用Ps与MSE 来量化SPAM 噪声对Shor算法的影响程度,分别如图5(c)和图6(c)所示.曲线中的每个点是实际计算的成功率大小,曲线则是对结果的拟合.通过曲线可以看出SPAM 噪声的影响是线性的.因为在线路中一共只会受到2t+n次SPAM 噪声的影响.理论上随着待分解整数比特数目增加,线路会更容易受到噪声影响,反映在图5(c)中是斜率的绝对值更大.然而模拟结果这种特征并不明显,主要原因在于分解的整数相差不大,相邻两个整数只相差了一位.并且由于测量次数与带分解整数二进制位数呈线性关系,导致图中拟合曲线斜率变化不明显.

4.3 热退相干通道

本文假定所有量子比特共享一组T1,T2,并且选择表2 中的大整数、随机数的组合进行模拟,对于每一个组合都模拟了在不同T1,T2组合下的算法运行.T1,T2参数选择如表3 所列,共100 组.在模拟中量子门的时间均设置为 50 ns .并且分别针对退相干通道中N=15,N=21,N=35 的分解实验重复了2000 次、4000 次以及8000 次.

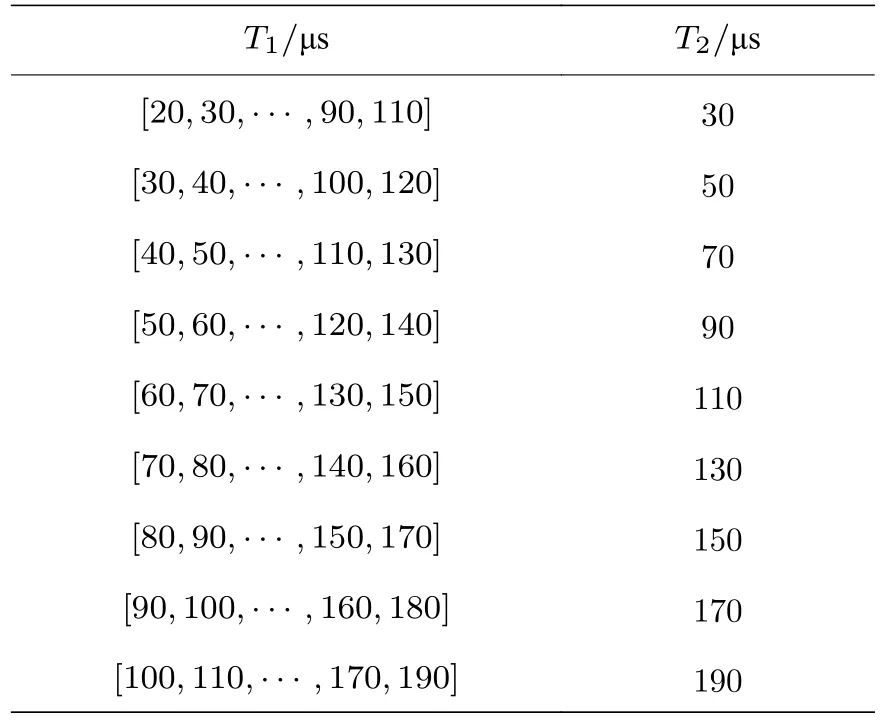
表3 退相干通道中 T1,T2 的取值Table 3.Choice of T1,T2 in TRC.

对比不同T1,T2对于分解N=15,N=21,N=35的|ψ4〉分布的影响,如图8 所示.

图8 热退相干通道中不同 T1,T2 对(N=15,a=2),(N=21,a=2),(N=35,a=2) 中的 |ψ4〉 概率分布的影响Fig.8.Different T1,T2 of TRC on probability distribution of |ψ4〉 in (N=15,a=2),(N=21,a=2) and (N=35,a=2).

随着退相干时间降低,每一组 |ψ4〉的峰值大小降低,分布也更混乱.待分解的整数越大,对应的|ψ4〉分布的峰值下降得越明显.与去极化通道的噪声类似,在模拟中每当量子比特经过一个量子门时都会按照(9)式发生热退相干.通过Ps以及MSE与退相干时间的关系可以更好地分析该类噪声对Shor 算法的影响,如图9 和图10 所示.

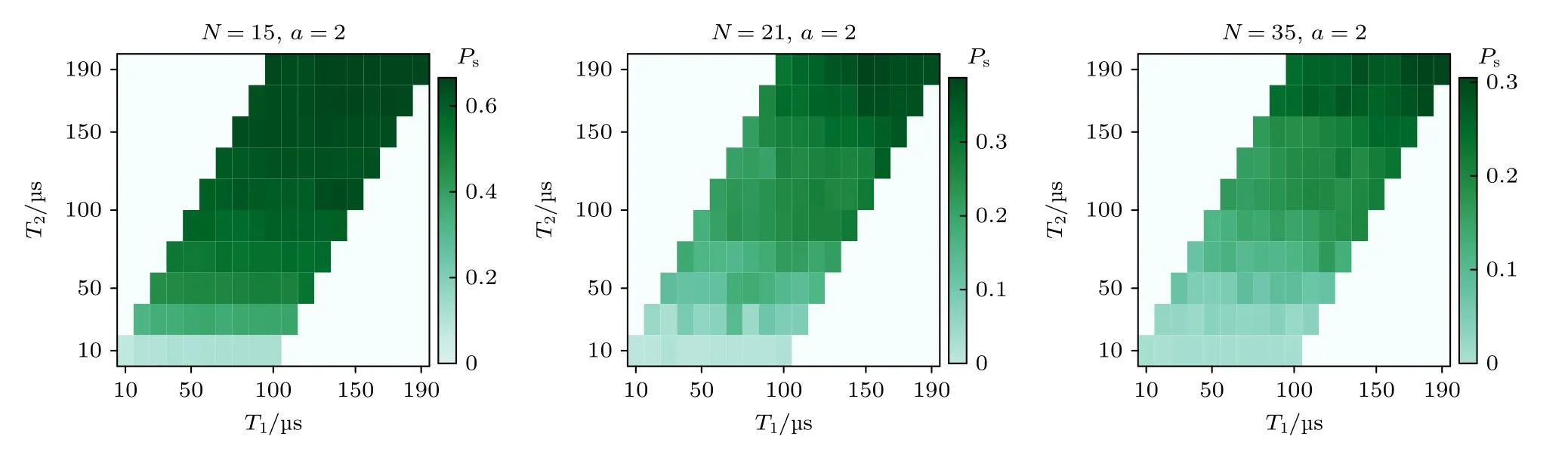
图9 Ps与热退相干通道的噪声的关系Fig.9.Effect of noise in TRC on Ps.

图10 MSE 与热退相干通道的噪声的关系Fig.10.Effect of noise in TRC on MSE.

图9 中白色区域是没有数据的点.其他区域里颜色越深代表该T1,T2条件下的成功率越高.随着T1,T2增大,成功率逐渐增大,并且随着待分解整数比特数目增多,更容易受到退相干噪声的影响,其成功率随着T1,T2变化而波动的幅度相对更大.图10 则是MSE与T1,T2的关系.

图10 中白色区域是没有数据的点.其他区域里颜色越深代表该T1,T2条件下的MSE 越高.随着T1,T2增大,成功率也逐渐增大,对应的MSE逐渐降低.

5 总结与展望

本文将Shor 算法测量得到预期结果的概率之和作为Shor 算法整数分解的成功率,发现概率之和与均方误差的高低能够准确评估Shor 算法中量子线路的运行结果的优劣,在此基础上开展了一系列针对不同类型的噪声与成功率关系的研究.分别研究了去极化通道、状态制备与测量通道、热退相干通道的噪声对Shor 算法的影响,并且在经典计算机上开展模拟Shor 算法分解整数的实验.对于任一通道,设置了不同噪声大小,得到了不同噪声大小与算法成功率的数值关系.模拟结果表明,在去极化通道中成功率随着噪声增大呈指数降低.受量子线路搭建方式的影响,成功率随双比特门去极化噪声增大而降低的趋势快于单比特门去极化噪声.而状态制备与测量通道中的噪声对于成功率的影响是线性的.相同噪声大小情况下,随着待分解的整数比特位数增多,需要的量子线路更加复杂,线路深度以及宽度都将增加,导致成功率随噪声增大而下降得更快.在真实量子计算机中运行Shor算法时,必须使用一系列的纠错手段进行纠错,并且需要将纠错重点放在去极化噪声中.此外,对于Shor 算法的量子线路进行优化与改进能够有效地降低线路复杂度,并且有助于减弱算法运行时各类噪声对量子线路的影响,如使用近似QFT 代替精确QFT 或者使用加窗以及陪集表示等方式都能够降低线路复杂度,从而减弱因噪声引起的误差.未来我们将针对优化后的线路进行纠错,探究在使用纠错算法的基础上量子线路的复杂度以及噪声对线路的影响.

柠檬果醋的L值、a值和b值使用色差计进行测定。色差计使用前需要用较厚的白纸进行校准。ΔL值表示亮度；Δa值正值偏向红色，负值偏向绿色；Δb值正值偏向黄色，负值偏向蓝色。通过公式ΔE=(ΔL2+Δa2+Δb2)1/2来计算总色差。ΔE在0～0.5时，色差可以忽略，肉眼很难辨认；ΔE在0.5～1.0时，色差值很低，只有长期训练的人才能观察出；ΔE在1.0～1.5时，色差值属于中等；ΔE>1.5时，色差严重。

感谢中国电子科技集团公司第三十二研究所量子创新中心的陈鑫淼与高薪凯对搭建Shor 算法量子线路的讨论,同时感谢邢耀文以及姚晓梅对量子噪声建模提供的思考以及对论文撰写提供的指导.

附录A

附录A 详述了连分数(continuous fraction)的原理,记作 Fraction() .在测量得到l后,需要计算 F raction(l/j),结果记作k/r,其中k是正整数,r是a的阶.有限项的常规连分数(简称连分数)满足以下的约束条件:∃N∈N,∀k∈N:aN+k=0,因此也可以写成如下形式:

在Shor 算法中,将l/j记作g,根据(A1)式可以将任意一个小于1 的正有理数其写成如下形式:

其中g1,g2,···,gM是正整数,如果在某一个gi将其截断,舍弃掉一些小数,便可以得到该数的一个收敛,如

随着gi的增加,被舍弃的部分越来越小,这些收敛值也越来越近g.在Shor 算法中,需要找到一组收敛[g1,g2,g3,···,gi],使得i足够大的同时满足有理数的分母gi也要小于N.最后得到的分母可能就是Shor 算法量子部分的最后结果r,即 1/[g1+1/(···+1/gi)]=k/r.

附录B

图B1 和图 B2 给出了分解N=15,N=21,N=35 的实验中Ps和MSE 与去极化通道中单比特门噪声的关系.

图B3 和图 B4 给出了分解N=15,N=21,N=35 的实验中Ps和MSE 与去极化通道中双比特门噪声的关系.

图B1 分解实验中 Ps 与去极化通道中单比特门噪声的关系 (a) N=15;(b) N=21;(c) N=35Fig.B1.Effect of noise of one-qubit gate in DC on Ps of factoring:(a) N=15;(b) N=21;(c) N=35.

图B5 和图 B6 给出了分解N=15,N=21,N=35 的实验中Ps和MSE 与状态制备与测量通道中噪声的关系.

图B7 和图 B8 给出了分解N=15,N=21,N=35 的实验中成功率和MSE 与退相干通道中噪声的关系.

表B1 给出了分解所有(N,a)组合的线路参数以及在不同噪声的环境下的成功率.