基于相对拟牛顿法的自卫式欺骗干扰抑制算法

齐美彬,赵 谦*,徐 晋,项厚宏,杨艳芳,崔国龙

(1. 合肥工业大学 计算机与信息学院, 安徽 合肥 230009)(2. 中国电子科技集团公司第三十八研究所, 安徽 合肥 230088)(3. 合肥工业大学 物理学院, 安徽 合肥 230009)(4. 电子科技大学 信息与通信工程学院, 四川 成都 611731)

0 引 言

主瓣干扰[1]的存在导致雷达系统的目标检测性能显著下降,近年来受到广泛关注[2-7]。作为一种有效的主瓣干扰技术,自卫式欺骗干扰[8]是由搭载于目标上的干扰机对雷达发射信号进行截获、存储、调制及转发产生的假目标信号,该干扰在空间角度上与目标完全一致,且与真实目标高度相似,传统的主瓣干扰抑制算法难以对其进行抑制。

为了抑制与目标同角度的干扰信号,构建有效的雷达系统是一个常用的策略。理想的雷达系统可以扩大目标与干扰之间的差异性,为抑制干扰提供条件。文献[9-10]引入频率分集阵列 (FDA) -多输入多输出 (MIMO) 雷达系统,利用距离维自由度对接收信号中的真假目标进行区分。但是文献[9-10]需要已知目标的距离和角度等先验信息,在实际战场环境下该条件难以满足。文献[11]利用FDA-MIMO雷达的距离-角度二维依赖性,通过基于最大信噪比 (SNR) 的盲源分离 (BSS) 算法从接收信号中分离出目标信号,实现在没有任何先验信息的前提下对同角度欺骗干扰的抑制效果。但是由于MIMO雷达的功率利用率低,该方法在低SNR的情况下干扰抑制效果较差。文献[12]引入极化单输入多输出 (PSIMO) 雷达系统,利用接收信号的极化自由度,采用基于特征矩阵联合对角化 (JADE) 的BSS算法,达到了抑制同角度干扰的效果。PSIMO雷达适用于低SNR场景,但是该方法只针对压制干扰,没有考虑自卫式欺骗干扰的抑制问题。

BSS算法主要利用目标回波与干扰信号之间的独立性,通过估计分离矩阵将目标信号和干扰信号分离在不同的通道上。该算法可以直接对接收信号进行处理,且需要的先验信息较少,具有很强的实用性,近年来成为了主瓣干扰领域的热门算法[13-16]。文献[17]首次在主瓣干扰抑制领域使用了基于高斯矩的BSS算法,实现了噪声干扰的抑制。文献[18]采用基于JADE的BSS算法,提升了干扰抑制的效果。文献[19-20]采用基于高阶统计量的BSS算法分离出目标信号,并利用分离出的目标信号估计出目标的距离和到达角等信息,实现了主瓣压制干扰下的目标检测。文献[17-20]所采用的BSS算法均高度依赖于源信号之间的相互独立性,而在自卫式欺骗干扰场景下干扰与目标分量之间的独立性严重降低,这会导致以上算法估计分离矩阵的性能降低,甚至失去抑制干扰的作用。

针对上述问题,本文在PSIMO雷达系统下提出了一种自卫式欺骗干扰抑制算法。该算法在PSIMO雷达的基础上构建重叠子阵模型,通过对各子阵白化后的信号计算自相关从而构建出三维联合自相关矩阵,并采用相对拟牛顿法准确估计出分离矩阵,进而实现分离目标和干扰信号的效果。本文算法对独立分量信号模型依赖性较低,能够有效抑制自卫式欺骗干扰,仿真结果验证了本文算法的有效性。

1 基于PSIMO雷达的子阵信号模型

1.1 PSIMO雷达信号模型

考虑如图1所示的PSIMO雷达系统[12],由1个极化发射天线和L个极化接收天线组成的间距为的均匀线阵构成。

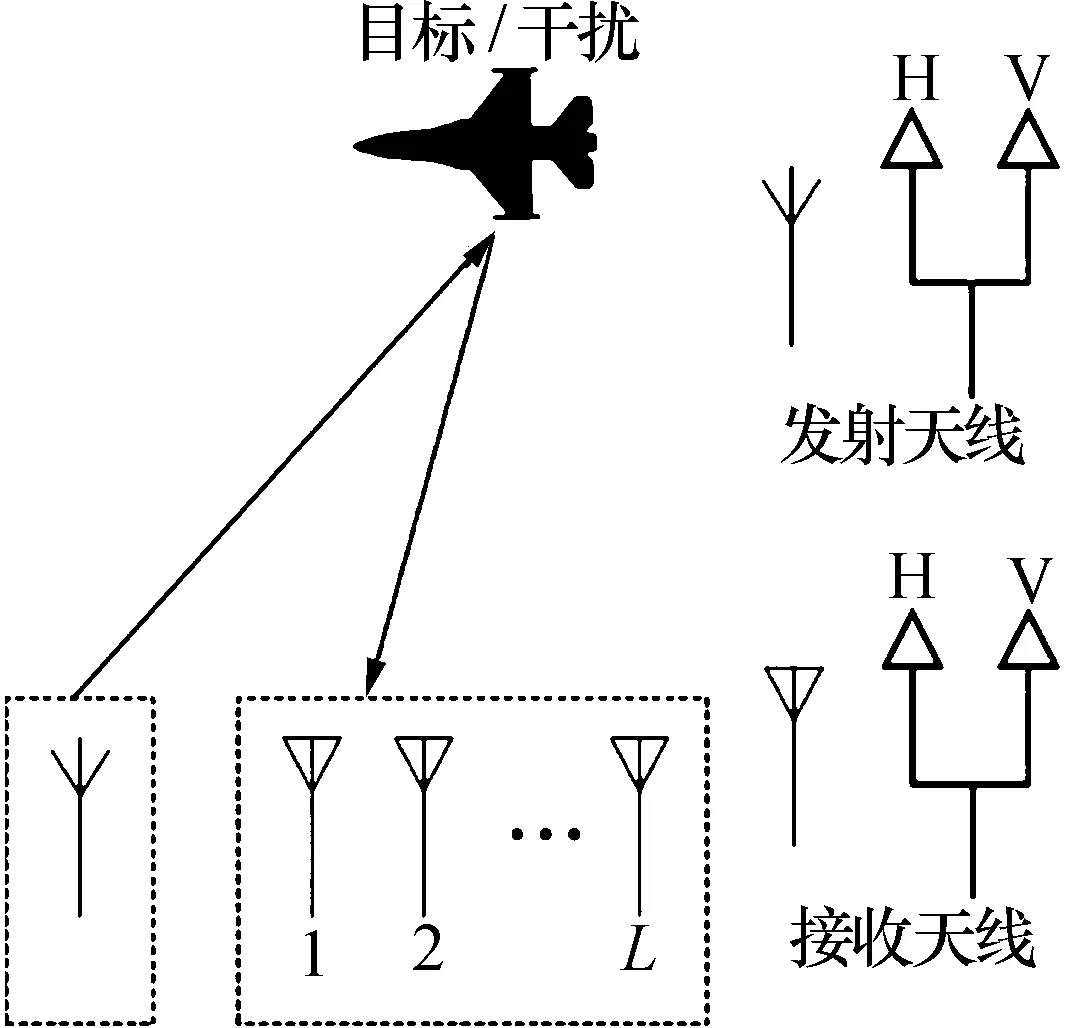
图1 PSIMO雷达系统示意图Fig.1 PSIMO radar system schematic

发射信号采用线性调频信号,信号形式如下

s(t)=sT(t)exp(j2πf0t)

(1)

式中:f0为发射信号中心频率,时间t∈[0,Tp];Tp为脉冲宽度;sT(t)表示线性调频信号的复包络。对于带宽为B的线性调频信号,调频系数μ=B/Tp,则sT(t)可以表示为

(2)

PSIMO雷达发射天线的极化矢量表示为Γt=[Γh,Γv]T,第l个接收天线的极化矢量rl=[rlh,rlv]T,l=1,2,…,L。考虑雷达探测范围内存在一远场目标,假设目标至雷达的距离为Rt,空间角度为θt,目标信号幅度为β,S是目标的散射矩阵,具体表示为

(3)

则L个阵元接收到的回波信号可以表示为

(4)

式中:⊙表示Hadamard积;c为光速。R=[r1,r2,…,rL]T是由接收阵列极化矢量构成的矩阵,阵列流形矩阵A=[a(θt),a(θt)],其中导向矢量

(5)

欺骗干扰是由干扰机截获的雷达波形经过数个短时延后,再由机载发射天线转发出去,使其产生不同的距离偏移,从而生成多个假目标干扰。考虑部署于目标上的自卫式干扰机,其接收天线极化矢量为rJ=[rJh,rJv]T,发射天线极化矢量为ΓJ=[ΓJh,ΓJv]T。则干扰机接收到的雷达信号

(6)

假设干扰机共计转发P个欺骗干扰,第p个干扰的转发时延τpJ,θJ表示干扰信号的到达角度,在自卫式欺骗干扰中θJ=θt。干扰信号可以表示为

(7)

则L个阵元接收到的干扰信号

(8)

式中:γ是干扰信号的幅度。流形矩阵AJ=[a(θJ),a(θJ)],其中导向矢量表示为

(9)

因此,L个阵元的总接收信号为

XL(t)=XT(t)+XJ(t)+NL(t)=Cg(t)+NL(t)

(10)

(11)

1.2 重叠子阵模型

重叠子阵是一种虚拟阵列技术,一般采用均匀的子阵结构,不同子阵间存在复用的阵元。本文在PSIMO雷达系统下构建如图2所示的重叠子阵结构,将由L个接收天线组成的均匀线阵分成K个重叠的子阵列,每个阵列包含个阵元,则有K=L-M+1。

图2 重叠子阵结构示意图Fig.2 Diagram of overlapping subarray structure

故第k个子阵的接收信号可以表示为

Xk(t)=Ckg(t)+Nk(t)

(12)

传统雷达系统下的BSS依赖于空间角度信息,在干扰和目标角度完全相同时无法分离出源信号。基于PSIMO雷达的重叠子阵信号模型提供了接收极化自由度,混合矩阵Ck满秩,为使用BSS进行干扰抑制创造了条件。

2 基于相对拟牛顿法的BSS算法

2.1 BSS算法介绍

BSS是一种对多通道数据进行无监督检测的技术,其依赖于源信号之间相互独立的混合信号模型Y=AX,通过估计分离矩阵B,进而从混合信号Y中分离出源信号,即X=BY。BSS算法的处理流程如图3所示。

图3 BSS算法处理流程Fig.3 BSS algorithm processing flow

信号的预处理包含白化和计算自相关矩阵两个部分。白化处理可以使各信号分量互不相关,提高BSS算法的分离效果[21]。对白化后信号求自相关可以得到自相关矩阵Z,利用对角化算法可以估计出分离矩阵B。

本文在PSIMO雷达子阵信号模型的基础上,提出了一种基于相对拟牛顿法[22]的BSS算法。对于子阵信号预处理生成的三维联合自相关矩阵Z,相对拟牛顿法的任务是找到一个矩阵B使得BZBT(BZ1BT,BZ2BT,…,BZKBT),包含尽可能多的对角化矩阵。当矩阵集Z可联合对角化时,该算法具有二次收敛性。因此,基于相对拟牛顿法的BSS算法的流程如下。

步骤1 预处理。对K个子阵的接收信号矩阵进行白化处理得到白化信号Wk(t),k=1,2,…,K,并分别计算出自相关矩阵Zk,从而构造出三维联合自相关矩阵Z=(Z1,Z2,…,ZK)。

步骤2 相对拟牛顿法估计分离矩阵。相对拟牛顿法构造了基于二阶导数集 (Hessian矩阵) 的平均对数似然函数,首先根据联合自相关矩阵Z计算出相对梯度矩阵和相对Hessian矩阵的近似,然后利用Hessian矩阵的稀疏对角结构计算出平均对数似然函数的牛顿方向 (下降方向),最后采用回溯线性搜索法迭代更新分离矩阵从而最小化似然函数,函数收敛后即可估计出分离矩阵。

步骤3 分离信号。利用分离矩阵与白化信号对源信号进行估计,实现信号分离。

2.2 预处理

信号白化过程可以通过以下方式进行。

Wk(t)=QkXk(t)=QkCkg(t)+QkNk(t)

(13)

式中:Wk(t)是第k个子阵接收信号的白化信号矩阵;Qk∈CN×M是白化变换矩阵,此处N=2表示目标回波和干扰信号两个分量。白化变换矩阵可以由以下公式给出。

(14)

(15)

对K个子阵接收信号计算得到的自相关矩阵集(Z1,Z2,…,ZK)构成一个三维联合自相关矩阵Z∈CN×N×K,对Z进行有效的联合对角化处理即可估计出分离矩阵。

2.3 相对拟牛顿法估计分离矩阵

相对拟牛顿法的损失函数通过一个平均对数似然函数给出。

(16)

为了从最大似然的角度解决联合对角化问题,算法需要最小化损失函数L(B)。L(B)的泰勒展开可以描述其关于B的相对变化。

(17)

式中:〈·|·〉表示矩阵的欧式标量积,即〈X|Y〉=Trace[XTY];G是相对梯度矩阵,其大小为N×N;张量H是相对Hessian矩阵,其大小为N×N×N×N。当独立分量信号模型不能完全成立时,G和H共同决定了损失函数的下降方向。Di表示对角化后的自相关矩阵,即Di=BZiBT,i=1,2,…,K,则

(18)

(19)

式中:a,b,c,d表示矩阵和张量的下标,当a=b时相对系数δab=1,否则δab=0。从结构上来看,H只有N3阶非零系数,因此是稀疏的,但是其计算复杂度过高,为O(N3×K)。考虑计算相对Hessian矩阵H的近似为

(20)

(21)

相对拟牛顿法对独立分量信号模型依赖性较低,在自卫式欺骗干扰场景下可以快速准确地估计出分离矩阵B。另外,本文采用的重叠子阵结构可以有效改善自适应算法的统计特性[23],能够提高相对拟牛顿法的估计效果。

2.4 信号分离

根据相对拟牛顿法估计的分离矩阵B,可对源信号矩阵进行估计。第k个子阵的源信号估计可以表示为

(22)

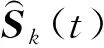
3 仿真实验

由于目前实验条件的限制,难以获取实测数据,因此本次实验采用仿真数据对所提算法进行验证与分析。在未来的工作中,我们将进一步结合实际工程应用进行深入研究。

3.1 仿真参数设置

雷达的接收阵列是由10个阵元构成的均匀线阵,阵元间隔为半波长。子阵个数设为3,每个子阵包含8个阵元。设置PSIMO雷达发射天线的极化矢量为

(23)

接收阵列的极化方式需要提供极化自由度,因此将接收极化矢量设置为

R=r1,r2,…,rm=

(24)

目标散射矩阵设置为

(25)

考虑实际战场情况下,干扰机存在截获雷达发射信号所有信息的可能性,包括发射天线的极化矢量ΓJ=Γt,因此在实验中令干扰机的发射天线极化矢量,干扰机接收和发射采用同一根天线,即rJ=ΓJ。其他参数设置如下。

如表1所示,远场环境下存在一个真实目标,位于目标上的干扰机产生4个假目标干扰,SNR远小于干噪比 (JNR),即干扰幅度远大于目标幅度。接收信号的脉冲压缩结果如图4所示,由图可以看出目标所在距离单元的谱峰消失,真实目标被完全淹没。

表1 仿真参数Tab.1 Simulation parameters

图4 接收信号脉压结果Fig.4 The pulse compress result of the received signal

3.2 有效性实验结果及分析

为验证PSIMO雷达系统对自卫式欺骗干扰抑制的有效性,分别对传统SIMO雷达和PSIMO雷达的接收信号,采用本文算法分离出目标通道和干扰通道,两个通道的脉冲压缩结果如图5所示。

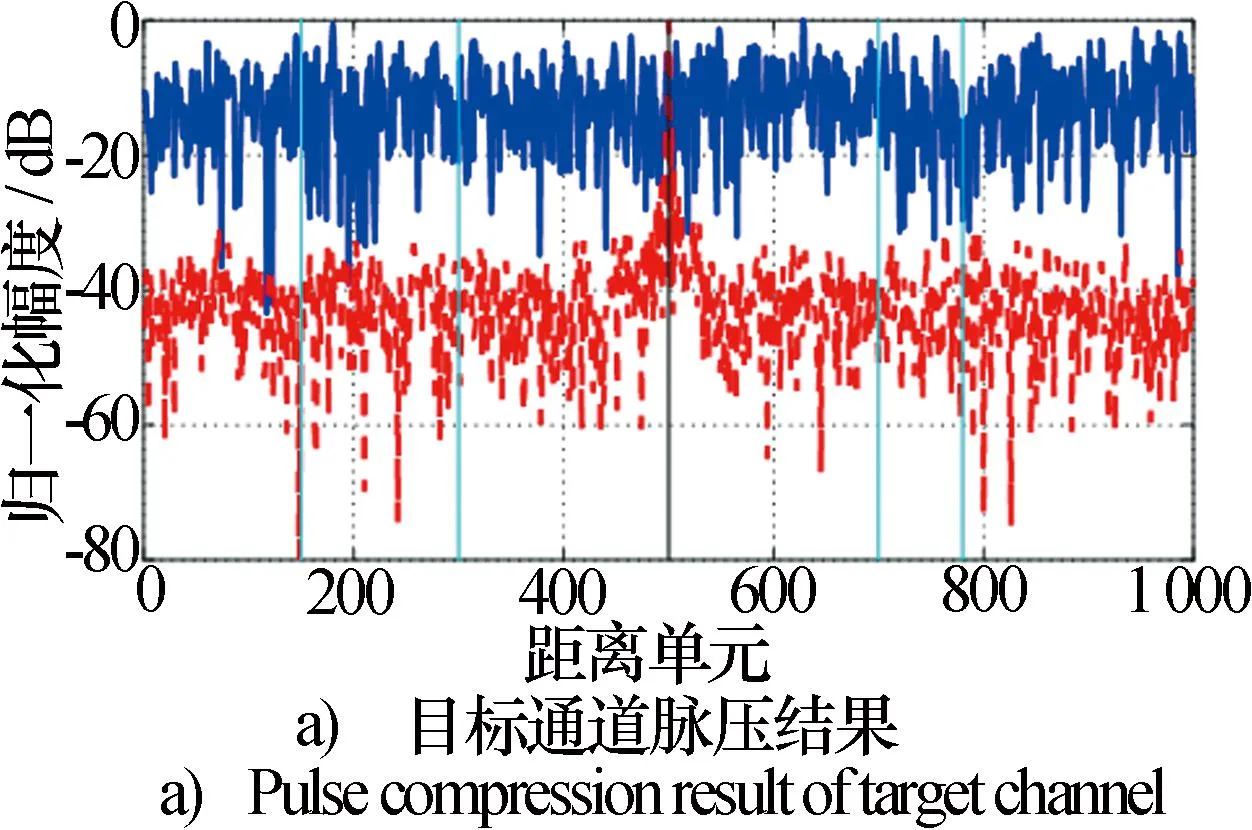
图5 传统SIMO和PSIMO分离结果Fig.5 Traditional SIMO and PSIMO separation results

对比传统SIMO雷达和PSIMO雷达的处理结果,前者的目标通道和干扰通道在目标距离单元位置均未出现明显的谱峰,没有成功分离出目标信号。在PSIMO雷达系统下,分离得到的目标通道经过脉冲压缩后,在目标距离单元处存在明显的谱峰,而干扰距离单元处的谱峰完全消失,同时在干扰通道上只有干扰距离单元处存在谱峰,目标信号和干扰信号被成功分离在不同通道上,实现了干扰抑制的效果。图5有效地验证了PSIMO雷达系统下本文算法在抑制自卫式欺骗干扰问题上的有效性。

为了进一步验证本文算法的有效性,将本文算法与文献[12,17-18]进行了对比实验。文献[17-18]采用的是传统的盲源分离算法,文献[12]对PSIMO雷达的接收信号采用JADE算法对压制干扰进行抑制。本次实验中,文献[12,17-18]都只考虑自卫式欺骗干扰。图6展示了在SNR=10 dB,JNR=80 dB时四种算法的干扰抑制结果。

图6 算法分离结果Fig.6 Algorithm separation results

由图6可以看出,文献[17-18]传统的基于BSS的方法无法分离出目标信号。自卫转发式干扰的空间角度与目标信号完全一致,因此传统SIMO雷达系统中,混合矩阵不是满秩的,盲源分离算法失效。文献[12]和本文算法考虑了极化信息,混合矩阵满秩,因此可以将目标信号和干扰信号分离在不同的通道上。图6展示了文献[12]和本文都具有较好的分离效果,但从干扰通道的脉压结果来看,本文算法在目标距离单元附近的幅度更低,即干扰通道中目标信号的分量更少。

在实际战场环境下,密集自卫式欺骗干扰较为常见,这就要求抑制算法能在转发时延较低的情况下依然能达到抑制效果,即具有良好的鲁棒性。针对密集自卫式欺骗干扰,将干扰距离单元设置为[369,435,586,651],图7展示了在SNR=10 dB,JNR=80 dB时四种算法的干扰抑制结果。

图7 密集干扰下算法分离结果Fig.7 Algorithm separation results under dense interference

从图7可以看出,文献[17-18]依旧无法达到抑制干扰的效果。在密集干扰场景下,自卫式欺骗干扰信号与目标回波存在大量的时域重叠部分,严重降低了源信号之间的独立性。文献[12]采用的基于JADE的BSS算法严重依赖于独立分量信号模型,因此在文献[12]分离得到的目标通道和干扰通道中,目标距离单元和干扰距离单元处均存在明显的谱峰,未能完全抑制干扰信号。而本文算法对源信号之间的独立性依赖性更低,在分离得到的目标通道中,只有目标距离单元处存在明显谱峰,干扰信号被完全抑制。因此,在密集自卫式欺骗干扰场景下,较于文献[12,17-18]三种方法,本文算法仍然能保持较好的干扰抑制效果,且抑制性能不受干扰距离单元的影响,具有良好的鲁棒性。

3.3 性能分析

雷达接收信号的信噪比会干扰抑制算法的抑制效果,为了分析本文算法与文献[12,17-18]的在不同输入SNR下的表现,本文针对非密集自卫式欺骗干扰进行了两组统计对比试验。

目标通道的信干噪比 (SJNR) 作为衡量干扰抑制算法的重要指标之一,是指信号中目标信号与干扰和噪声之和的比。设定JNR=80 dB,图8a)展示了1 000次蒙特卡洛实验后,不同的输入SNR下四种算法目标通道脉压后的输出SJNR的统计结果。

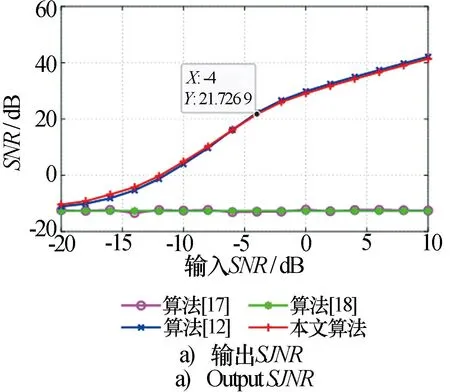
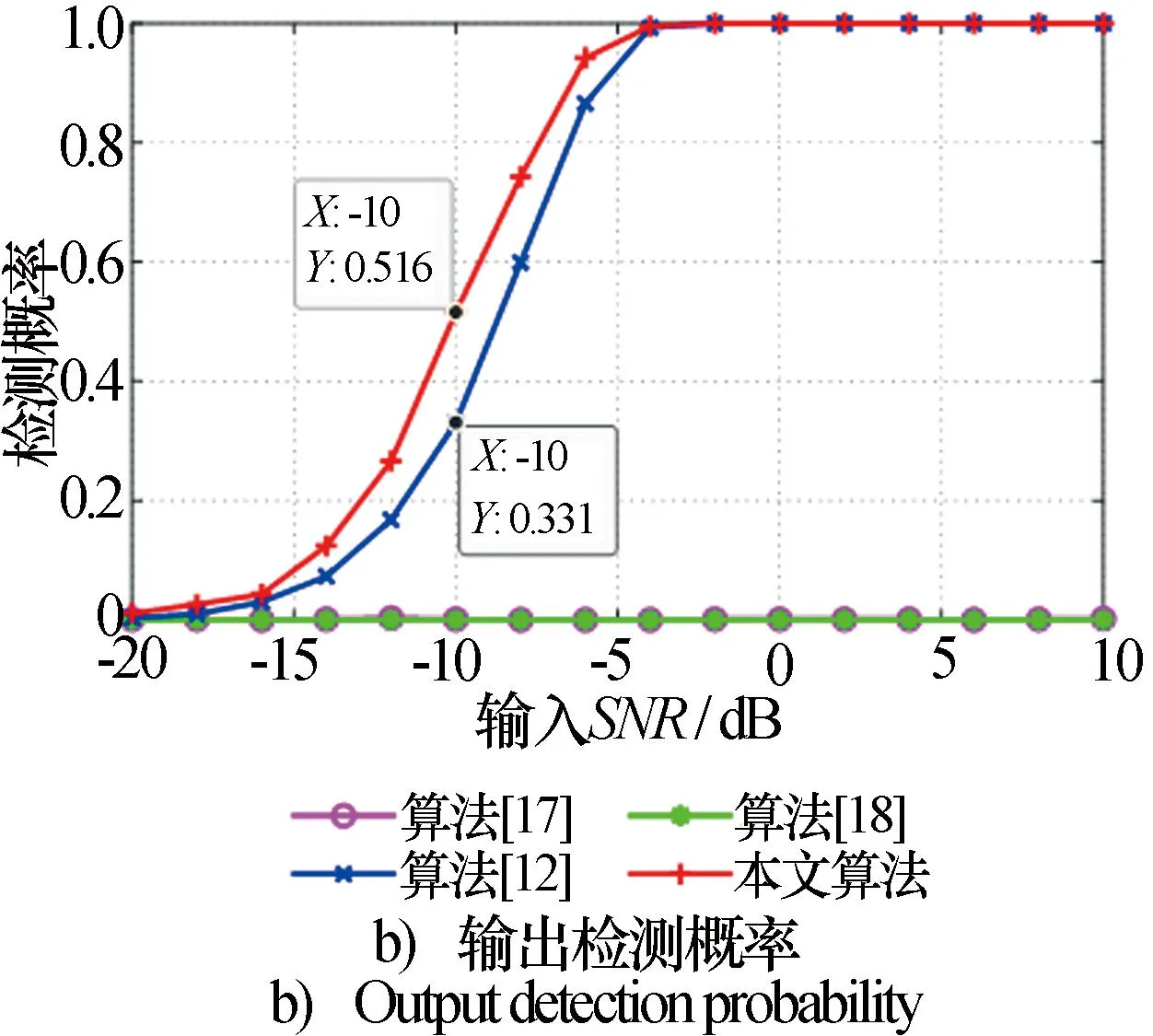
图8 输入SJNR对算法性能的影响Fig.8 Effect of input SJNR on algoirthm performance

从图8a)可以看出,由于文献[17-18]对同角度的干扰无效,分离后得到的目标分量非常小,因此SJNR一直保持在-12 dB左右。在非密集自卫式欺骗干扰下,文献[12]和本文算法所得到的曲线非常接近,且在输入SNR为-4 dB时,分离后脉压的SJNR达到了21 dB以上。

主瓣干扰的作用是为了降低雷达的目标检测性能,因此分离后的目标检测概率也是衡量干扰抑制算法性能的重要指标之一。同样将输入JNR设置为80 dB,对不同输入SNR下分离的目标通道进行目标检测,1000次蒙特卡洛实验统计得到的目标检测概率如图8b)所示。

仿真结果表明,一方面,文献[17-18]分离后的检测概率均接近0,再次证明了传统SIMO雷达系统下盲源分离对自卫式欺骗干扰无效。文献[12]和本文算法分离后的目标检测概率均随着输入SNR的增加而提高,且均在-2 dB时达到100%。另一方面,在输入SNR低于-2 dB时,本文算法的目标检测概率曲线明显高于文献[12]。在SNR为-10 dB时,文献[12]分离后的检测概率只有33.1%,而本文算法可达到51.6%,算法性能提升了18.5%。

由图8a)和图8b)可以看出,在非密集自卫式欺骗干扰下,本文算法可以有效抑制干扰信号,输入SNR越高抑制效果越好。在输入SNR低于-2 dB时,相较于算法文献[12],本文算法拥有更好的干扰抑制性能。

为了验证不同子阵个数K对本文算法性能的影响,在10阵元的PSIMO雷达系统下设置K=2,3,…,9,对应的子阵内阵元个数分别为M=9,8,…,2,SNR=10 dB,JNR=80 dB,在1 000次蒙特卡洛实验下分别统计输出目标通道的平均SJNR以及算法平均运算时间,统计结果如表2所示。

表2 不同子阵个数下的算法性能Tab.2 Algorithm performance under different number of subarrays

从表2可以看出,当子阵个数设置为3时干扰抑制效果最优,此时输出平均SJNR达到38.80 dB。而当时算法的平均运算时间最短,仅为0.751 6 ms。另外,在的情况下,本文算法的输出SJNR均超过36 dB,且平均运算时间均低于1 ms,能够保持较好的分离性能以及较低的运算时间。

4 结束语

自卫式欺骗干扰的空间角度与目标完全一致,且与目标高度相似,导致传统BSS算法完全失效,无法对干扰信号进行抑制。针对这一问题,本文提出了基于相对拟牛顿法的自卫式欺骗干扰抑制算法,在PSIMO雷达系统下构建重叠子阵模型计算联合自相关矩阵,采用相对拟牛顿法进行联合对角化从而估计出分离矩阵,将目标信号和干扰信号分离在不同通道上,达到了干扰抑制的效果。仿真实验表明,在低SNR下,本文算法能够有效抑制自卫式欺骗干扰,并且在干扰密集的情况下依然能够分离出干扰信号,分离性能对干扰距离单元具有良好的鲁棒性。