基于概率的步行导致结构振动评估方法

李兆凡, 潘 斌, Mark SARKISIAN

(1 清华大学土木工程系，北京 100084；2 史基摩欧文美尔(上海)建筑设计事务所有限公司， 上海 200031；3 Skidmore，Owings &Merrill LLP，San Francisco，CA 94111)

0 引言

结构竖向自振频率与行人步行频率相同(或是其整数倍)时,结构会发生共振。评估步行导致结构竖向振动的方法,大致可以分为三种类型。第一种是基于公式的简化评估方法,例如中国的JGJ 3—2010[1]附录A、JGJ/T 441—2019[2]第5.3.1节、美国ATC设计指南1[3]和AISC设计指南11第一版、第二版[4](以下皆指第二版)。第二种是基于频域的方法,例如英国混凝土学会出版的CCIP-016[5]以及钢结构研究院出版的SCI publication P354[6](简称P354)。第三类是基于时域的方法,将步行荷载作为动力时程作用于结构,通过时程分析求解结构振动加速度,如JGJ/T 441—2019、AISC设计指南11、法国道路和高速公路技术研究部Sétra的设计指南[7]。Zivanovic[8]等对结构振动相关文献做了很好的总结。

上述方法都可以得到结构共振时产生的最大加速度,而无法得到加速度的概率分布。本文提出的评估方法可以评估共振加速度值出现的概率,从而对结构振动的风险做出更准确、全面的评估。

1 现有的评估方法

采用AISC设计指南11的算例4.5来对比现有方法及本文建议的基于概率的评估方法。算例为长度40英尺(12.192m)的室外天桥,桥面由两根平行的W21×44铰接钢梁支承。混凝土弹性模量采用放大系数1.35。阻尼比取0.01。

ISO 10137[9]附录C和ISO 2631-2[10]给出了不同环境下振动加速度的可接受标准。这个标准给出了一条与振动频率相关的加速度基准线,将结构振动加速度与基准线的倍数定义为反应系数。CCIP-016建议了可接受的反应系数限值,其中室外天桥为64,室内天桥为32,办公环境为8。

1.1 基本理论

行人引起的结构振动是步行周期荷载引起的有阻尼强迫振动[11-12]。将周期荷载通过傅里叶变换分解为一系列正弦函数:

Fh(t)=Pαhsin(2πhfwt+φh)

(1)

式中:Fh(t) 为周期荷载的第h阶分量;t为时间;P为行人重量,取700N;αh为第h阶分量的动力荷载系数,可以通过仪器实测来获取;h通常取1～4,更高阶的分量忽略不计;fw为行人的步行频率;φh为相位差,当h=1～4时,φh分别为0、-π/2、π、π/2。

当结构竖向自振频率fn与步行频率fw存在倍数关系,即fn=h·fw时,式(1)的第h阶分量与结构频率fn相同,引发结构共振,其跨中的稳态响应加速度为a:

(2)

式中:β为楼板结构阻尼比;We为楼板结构阻抗有效重量,对于简支梁We=0.5W,W为楼板结构的实际重量;g为重力加速度。

1.2 简化评估方法

简化评估方法根据楼面梁的挠度来计算其竖向自振频率(也可用有限元程序分析确定),然后用式(2)计算楼面梁竖向振动的最大加速度。AISC设计指南11取动力荷载系数为:

αh=0.83e-0.35h·fw

(3)

由于在有阻尼强迫振动达到稳态响应之前步行活动可能即已结束,并且激励位置和感知位置不一定都处在最不利位置,该指南建议对式(2)结果进行折减,折减系数对步行天桥取0.7,对楼面结构取0.5。

JGJ 3—2010附录A、JGJ/T 441—2019第5.3.1节的方法与AISC设计指南11一致,公式形式也相同。虽然简化方法只考虑引起共振的谐波分量,但是仍能够给出足够精确的结果。简化方法的局限是当结构比较复杂时(例如连续梁和长悬臂梁振动会引起相邻跨结构的振动),计算结构有效重量比较困难[13]。

1.3 基于频域的方法

CCIP-016、P354提供的方法类似。以CCIP-016为例,考虑正常步行频率区间1.0～2.8Hz,对共振反应的评估包括下列步骤。

第一步将步行荷载用傅里叶变换分解为式(1)的正弦波分量(通常也取前4阶)。两个指南建议的动力荷载系数αh见表1,其中fh=h·fw,为第h阶荷载分量的频率。

表1 CCIP-016与P354推荐的步行动力荷载系数

第二步使用有限元软件对结构进行模态分析,得到频率在15Hz以下的所有振型。

第三步,第h阶正弦荷载对第m阶振型引起的加速度实分量areal,h,m、虚分量aimag,h,m分别为:

(4)

(5)

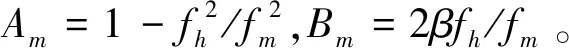
分别求和后,再计算结构加速度实分量峰值areal,h、虚分量峰值aimag,h以及对应的反应系数Rh:

areal,h=∑mareal,h,m

(6)

aimag,h=∑maimag,h,m

(7)

(8)

Rh=ah/aR=1,h

(9)

式中:ah为第h阶正弦荷载引起的振动加速度,aR=1,h为频率fh对应的基准加速度,即人对应该频率的振动时能感觉到的加速度阈值;Rh为反应系数。

第四步,将4阶荷载分量对应的反应系数和加速度进行SRSS组合,得到总的反应系数Rh及反应加速度峰值a。

(10)

(11)

CCIP-016和P354都通过分析实测数据,给出了步行荷载前4阶谐波分量的动力荷载系数,如表1所示,可见两本指南给出的系数比较接近。

按照CCIP-016的方法进行SAP2000建模分析,只有第1阶频率6.72Hz低于15Hz,因此只需要计算第1振型。采用1%阻尼比,最不利情形激励节点和反应节点都位于跨中,因此其振型位移ue,m和ur,m都为1。取步行频率为结构自振频率的1/3,即2.24Hz,此时计算得到的反应系数见表2。可以看到,主要的结构振动来自于第3阶正弦分量引起的结构共振。

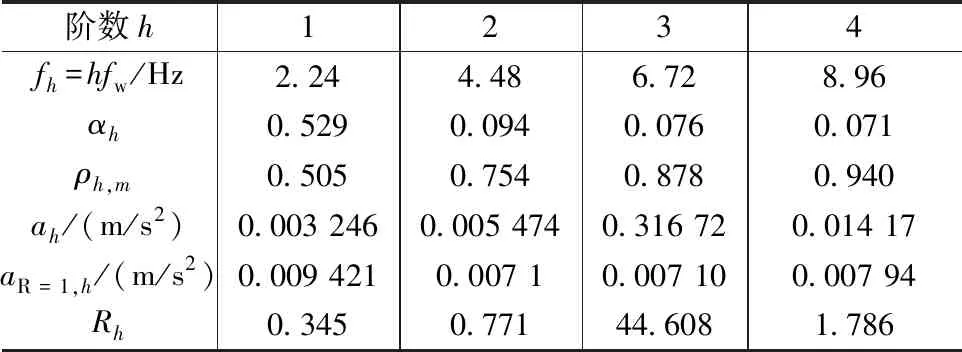
表2 根据SAP2000分析的频率通过CCIP-016方法计算反应系数

按式(10)SRSS组合得到总反应系数为44.7,小于CCIP-016推荐的室外天桥限值64,满足要求;按式(11)得到峰值加速度0.3171m/s2,与AISC设计指南11的计算结果比值为1.21。产生差异的原因将在1.4节讨论。

上述计算可以基于不同步行频率进行,从而得到不同频率步行激励下天桥结构的反应系数,见图1。可以看到曲线有两个峰值,分别对应结构自振频率6.72Hz的1/4和1/3,即1.68Hz和2.24Hz,一旦远离这两个频率,反应系数快速降低。

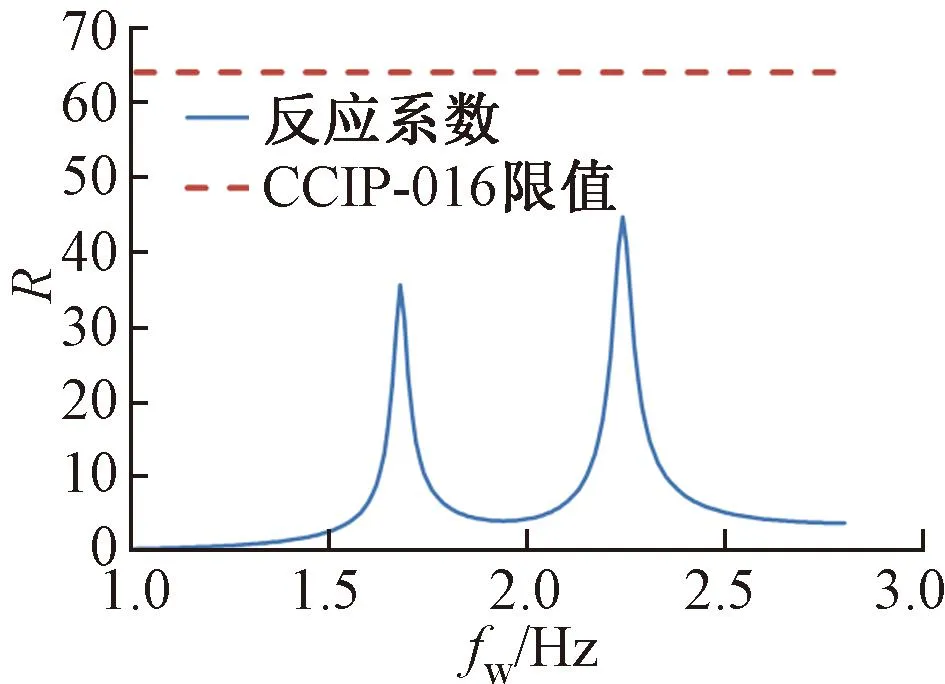
图1 天桥跨中节点的反应系数

1.4 基于时域的方法

CCIP-016推荐的式(4)动力荷载可以作为时程荷载施加于结构的激励节点,通过弹性时程分析求解结构反应。本例取h=3,则步行频率fw=fn/3=2.24Hz,位于常见的步行频率范围1.6～2.4Hz内。定义动力荷载并作用于SAP2000模型天桥跨中节点,采用1%阻尼比进行弹性时程分析,即可得到跨中节点的竖向加速度响应。从图2可以看到,加速度在步行开始后逐渐增大,最后稳态响应的最大加速度为0.3323m/s2。

1.5 三种方法的对比

三种计算方法的结果列于表3,如果以SAP2000时程计算结果为基准,可以看到AISC指南11结果偏差较大。

表3 三种方法计算的跨中竖向加速度

AISC指南11采用的动力系数为0.83e-0.35×6.72=0.079,折减系数对天桥取0.7。而CCIP-016的动力系数为0.033+0.0064×6.72=0.076,折减系数为ρh,m=1-e-2πβN=0.878。可以看到,两种方法动力系数和折减系数的差别是造成结果差别的原因。AISC设计指南11采用的动力系数随结构自振频率以指数形式递减,而CCIP-016采用的动力系数与频率之间是线性关系(h=1,2,3,4),见图3(a)。可以看到两者在较低频率段相差很大,在较高频率段差别稍小:在6.72Hz处,两本指南给出的动力系数相差不大,而在4.0Hz处(h=2,h·fw=4.0Hz),设计指南11给出的动力系数几乎是CCIP-016的两倍。

图3 AISCA设计指南11与CCIP-016的调整系数对比

在AISC设计指南11第二版的第7章,新增加了有限元方法分析楼板振动问题的说明,其中采用的动力系数参考了CCIP-016第2～4阶动力系数,并近似取为α=0.09e-0.075fn。

折减系数方面,AISC设计指南11对所有天桥取0.7(对楼面结构取0.5),而CCIP-016的折减系数是梁跨度的函数,跨度越长则折减系数越接近1.0。图3(b)显示了两个设计指南折减系数的对比。

2 基于概率的评估方法

2.1 步行频率的概率分布

本文第1节三种评估方法都能够得到步行荷载导致结构共振时结构所经历的峰值加速度,但是没有考虑共振发生的概率。对某一特定结构,只有特定频率的步行才会引发共振,而不同步行频率出现的概率并不相同。Matsumoto等[14-15]从统计的角度研究了505个行人步行频率,发现步行频率很好地符合正态分布(fw～N(μ,σ2)),其均值μ为1.99Hz,标准差σ为0.173Hz。步行频率的概率密度函数p(fw)为:

(12)

图4实线为统计数据,虚线为总人数与概率密度函数p(fw)乘积,可以看到两者非常接近。

图4 统计的505个步行频率

2.2 不超越概率的计算

对于某个结构,如果引发结构共振时的步行频率与1.99Hz相差越大,则其出现的概率就越低,因此在一个统计样本总体(如1 000次行人步行)中结构发生共振的概率就越低。

对结构按1.3节所述方法得到反应系数对于步行频率的函数R(fw) (图5(a))后,根据式(12)步行频率概率密度函数p(fw),就可以计算任意反应系数R的不超越概率,即保证率。定义二元函数h(fw,R):

(13)

图5 通过积分计算反应系数的保证率

对此函数在步行频率[1.0Hz,2.8Hz]范围积分,得到一个关于R的函数P(R),其含义即为结构反应系数低于R的保证率。

(14)

具体的计算方式为:对于任一给定的R值,通过图5(a)得到反应系数不超过R的频率范围(图中R=10),在图5(b)中计算相同频率范围对应的概率密度函数下方阴影区的总面积。对于本例天桥结构,得到的结果如图6所示。为方便仍以反应系数R为y轴,不超越概率P(R)为x轴。

图6 反应系数与不超越概率

最大的反应系数Rmax对应的不超越概率(保证率)为100%。本文建议根据结构类别取一定保证率的反应系数与限值比较来评估结构振动表现。办公建筑对振动要求高,建议取保证率为95%的反应系数,天桥建议取保证率为90%的反应系数。

对本例保证率为90%的反应系数为19.9,仅约为最大反应系数44.7的44%。保证率为95%的反应系数为30.5,约为最大反应系数的68%。图7显示了天桥竖向自振频率与反应系数的关系。改变钢梁刚度使竖向自振频率从1Hz变化到15Hz,对每个竖向频率,计算得到类似图7的结果,从而得到对应的峰值反应系数和90%不超越概率的反应系数,分别见图7的虚线和实线。可以看到,90%不超越概率反应系数曲线明显低于峰值反应系数曲线,同时结构竖向频率在3、5、7Hz附近时,不容易发生行人导致的结构振动,而结构竖向频率位于2、4、6Hz附近时,比较容易发生行人引起的共振。

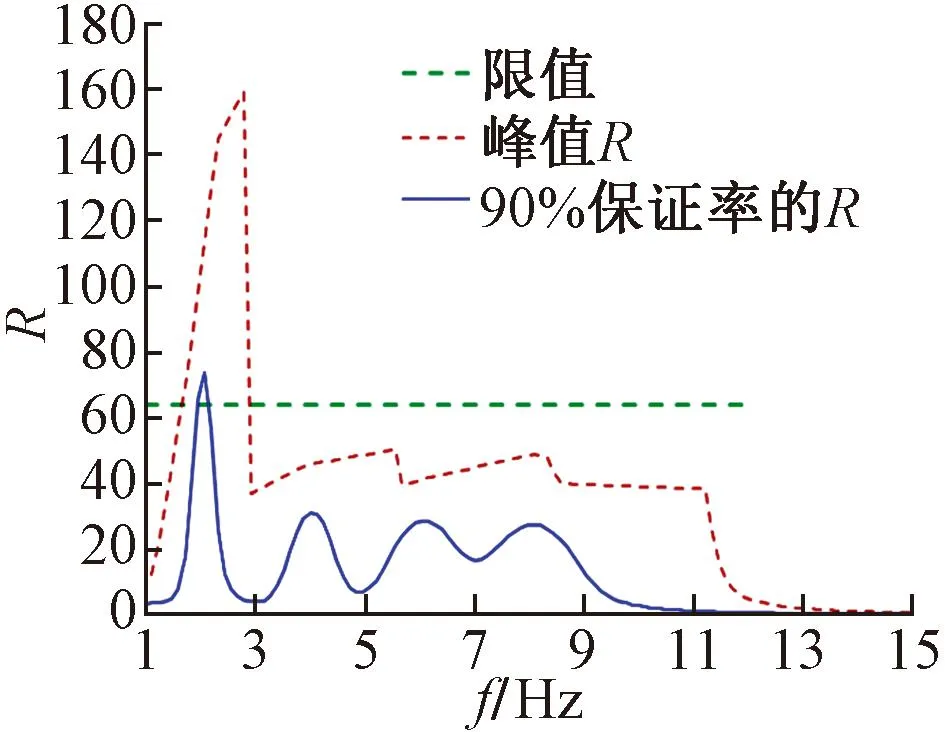
图7 结构竖向频率与反应系数关系

3 工程实例

洛杉矶某办公楼地上10层,建筑总高67m,建筑面积5.88万m2。建筑平面为正方形,边长约68m。楼面采用钢结构组合楼板,总厚度6.25英寸。楼面钢梁支承于剪力墙和钢吊柱之间,最邻近角部的柱位落在和轴线上,角落处没有布置柱位,因而整个角部板跨双向各悬挑10m(图8)。

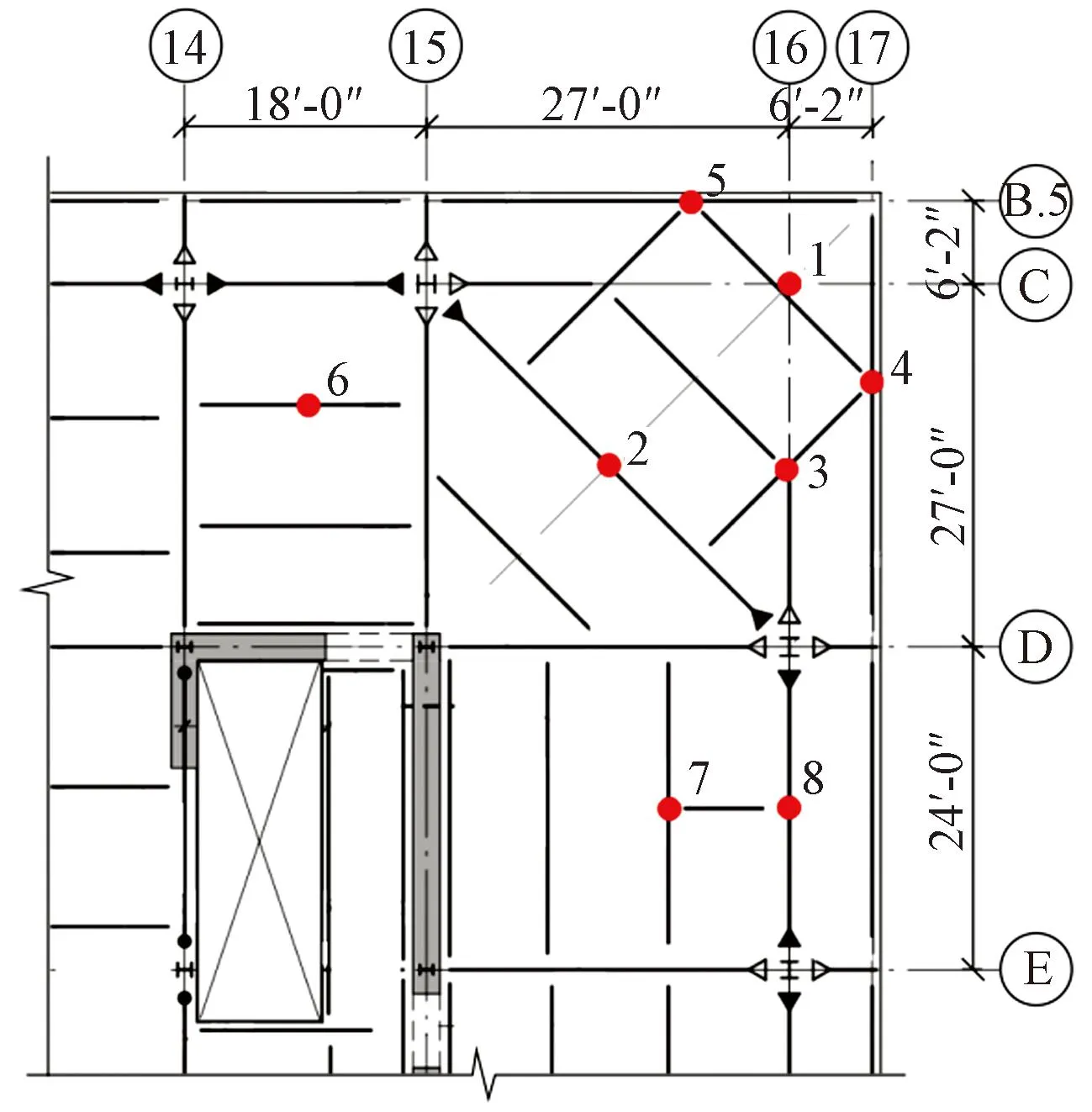
图8 楼层悬挑角部平面图(红色点为测点)

该办公楼项目施工工程中,在楼板完工、幕墙尚未安装、室内尚未装修时,工人在此悬挑角部行走时能够感觉到明显的楼面振动。业主因此对该处楼板建成后的性能感到担心,要求进行针对性的研究及测试。因此,笔者对楼板建成后的振动加速度进行了计算。悬挑结构有效质量、自振频率难以准确手算,此处不采用简化算法进行计算。

3.1 CCIP-016方法

按照CCIP-016的方法,采用ETABS有限元模型进行分析,前三阶模态的振型及频率如图9所示。

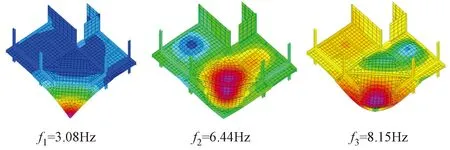
图9 悬挑角部的前三阶竖向振型及频率

考虑实际使用情况,最不利激励节点和反应节点都假设在距离楼板边8英尺处(图8中1号点)。选择步行频率为结构自振频率的1/2,即1.54Hz,采用3%阻尼比,对应的反应系数见表4,其中4阶荷载分量的4个Rh值按SRSS组合得到总的反应系数为7.2,接近但小于办公空间限值8,因此满足要求。加速度峰值0.0575 m/s2。

表4 根据ETABS分析的频率通过CCIP-016方法计算反应系数

考虑[1.0Hz, 2.8Hz]正常步行频率范围,得到悬挑角部1号点的反应系数曲线见图10。可以看到步行频率1.54Hz处对应峰值反应系数为7.2,但是在步行频率2.8Hz处反应系数更大,达到12.2。因此进一步计算了[2.8Hz, 3.5Hz]范围内的反应系数,可见步行频率3.08Hz处的反应系数高达46.3,远远超过可接受限值8。这是否会造成振动问题,显然CCIP-016方法难以做出回答。本文建议的基于概率的评估方法(见3.4节)发现,由于超过2.8Hz的步行频率极少出现,超过8的反应系数出现的概率极低,因此预计不会造成振动问题。

图10 悬挑角部1号点的反应系数

3.2 时程分析方法

按CCIP-016计算4阶正弦荷载,并叠加得到总的步行荷载,作用于ETABS模型中的楼面控制点,定义阻尼比为3%的弹性时程分析工况并运行分析,即可得到该节点的竖向加速度响应。可以看到,加速度在步行开始后迅速增大,然后逐渐进入稳态响应。稳态响应的最大加速度为0.0590m/s2。

CCIP-016的SRSS组合和SAP2000时程分析两种方法计算的步行频率为1.54Hz时竖向加速度如表5所示,分别相当于0.59%g以及0.60%g,超出规范限值0.50%g。

表5 两种方法计算的步行频率为1.54Hz时竖向加速度

3.3 基于概率的评估方法

按照本文第3节提出的基于概率的评估方法,分别按照步行频率范围[1.0Hz, 2.8Hz]以及扩大的频率范围[1.0Hz, 3.5Hz]计算反应系数与不超越概率关系,分别见图11(a)、(b)。

图11 反应系数与不超越概率

从图11可以看到,两种情况下最大反应系数差别很大,分别是12.2和46.3,但是按照图11所示,两种情况下具有95%保证率的反应系数几乎相同,都是3.5。反应系数超过办公室限值8的概率只有0.01%,基本可以忽略不计。这是因为步行频率在2.5～3.5Hz范围内的概率密度函数值非常低,因此导致楼板振动的概率很低。按照基于概率的评估方法,预计建成后此角部不会出现振动问题。

3.4 楼板振动现场测试

在AISC设计指南11编委Murray教授的指导下,其团队于2015年1月份完成了楼板振动舒适度实测工作[16]。现场选取了图8中8个位置进行竖向振动加速度记录,设置了三种经过最不利点的步行路线,包括沿南北向、沿东西向、沿着楼板边缘的“L”形路线。请工人以各种步行速度步行,记录的每分钟步数为90～143步,对应频率1.50～2.38Hz,同时采用Datastick VSA-1214加速度采集器和分析仪记录了各种行走频率下的楼板振动反应谱,并提供了分析报告。

现场共进行了图12所示四种情形下的测量,每种情形都是在前一种情形基础上的累加:1)只有结构楼板;2)布置混凝土砌块模拟附加楼面荷载;3)安装室内隔墙;4)沿楼板边缘放置钢筋模拟幕墙的重量。

图13 一次步行的测试结果

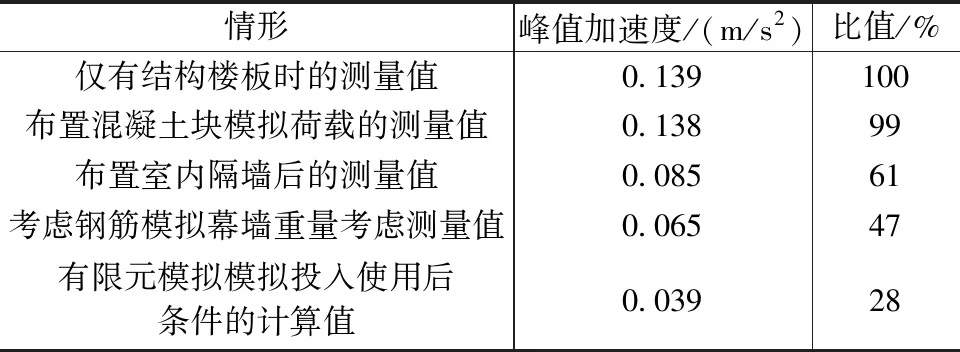
表6 测试报告给出的峰值加速度

测试无法模拟大楼竣工投入使用后情形,但是报告[16]也通过有限元分析模拟了使用后情形。当玻璃幕墙安装后楼板振动的阻尼会增加,按照3%等效阻尼比计算,测试报告预测峰值加速度将降到约0.039 m/s2,相当于0.40%g,舒适度满足要求。表6第三列是各种情形的峰值加速度相对比值,可以看到考虑各因素后峰值加速度逐步降低的过程。

3.5 小结

该办公楼在施工期间发现楼板振动问题,虽然施工阶段楼板振动性能并不能代表使用阶段,但是设计团队用不同方法评估了建成后楼板的振动性能。基于频域和时域的方法预测峰值加速度超过0.5%g。基于概率的评估方法发现振动超过可接受限值的概率极低,预计不会出现振动问题。进行了现场测试,结果表明施工期间峰值加速度确实很高,但是预测投入使用后加速度不会出现问题。

项目建成后,Murray教授团队在相同的悬挑角部再次进行了测试。结果显示峰值加速度仅约0.010 m/s2,约0.104%g,远小于限值0.5%g。可见外幕墙提供的刚度与阻尼远大于预计,已经基本消除了楼板振动问题。目前该大楼已经建成并使用5年以上,没有出现振动舒适度问题。

4 结论

(1)本文提出的基于概率的评估方法可以评估各加速度值或反应系数值出现的概率,更准确地评估楼板振动性能。

(2)建议有固定座位的办公等用途楼面采用具有95%保证率的加速度值或者反应系数来代表结构的振动表现。无座位的天桥等结构可以采用具有90%的保证率的数值。