基于无损检测的残损古建筑木结构受力性能研究*

白晓彬, 陈慧慧, 梁宁博, 刘崇焱, 杨 娜

(1 中冶建筑研究总院有限公司检测中心，北京 100088；2 北京交通大学土木建筑工程学院，北京 100044)

0 引言

中国古建筑木结构具有极高的文化、历史和艺术价值,按屋顶形式可分为庑殿、歇山、悬山、硬山、攒尖等。硬山式是古建筑中最普通和应用最广的形式,无论住宅、园林、寺庙中均有大量的硬山建筑。然而,古建筑木结构在服役过程中经历自然和人为因素的作用后会出现不同程度的损伤[1-2],如木材老化、表面开裂、构件腐朽、节点拔榫等现象。因此,通过检测确定结构的残损状况,并对残损状态下古建筑木结构的受力性能进行研究,进而对其结构安全状态进行评估是十分有必要的。

古建筑木结构常用的无损检测技术包括皮罗钉检测、应力波检测、超声波检测、微钻阻力仪检测等[3],其中应力波和微钻阻力仪检测是目前应用较为广泛的技术。20世纪90年代国外的Ross、Perllerin等[4-5]应用应力波对木制桥梁进行了检测,发现了木构件内部的腐朽。微钻阻力仪最早用于活立木的腐朽检测[6],后来逐步应用于古建筑木构件的缺陷检测。近年来,我国已经应用应力波和微钻阻力仪对清东陵[7]、谭柘寺[8]、雍和宫[9]、保国寺[10]等古建筑木构件进行了检测,解决了古建筑检测工作中的很多难题。

国内外学者对残损古建筑木结构的受力性能也已经进行了很多研究。在材料性能方面,高悦文、王晓欢、Yang N等[11-13]均进行过新旧木材的力学性能测试,结果表明旧木材的各项力学性能均有不同程度的降低。在节点受力性能方面,谢启芳等[14-15]分别对残损的斗拱和榫卯节点进行了抗震性能试验研究,研究了不同残损程度下节点的刚度退化规律。在结构整体受力性能方面,秦术杰等[16]进行了残损状态下明清井亭结构的动力特性和地震响应分析,结果表明,残损现象会降低结构的自振频率,增大地震作用下结构的位移和加速度。

目前已有的研究中,针对古建筑木结构整体受力性能的研究大都是基于理想模型,这些研究结果和结构的实际状况往往有所偏差。对于残损结构的研究大都集中在材料退化和残损节点方面,而有关古建筑木结构在残损状态下的整体受力性能则研究较少。为获得更接近实际状况的古建筑木结构的计算模型,赋予每个构件更精准的材料、几何信息,研究残损现象对古建筑木结构整体受力性能的影响,本文以北京市某硬山式古建筑为研究对象,首先对其进行现场无损检测,对结构的损伤状况进行量化,然后基于检测结果建立带有残损的结构有限元模型,研究残损状态下硬山式古建筑的静力性能和抗震性能,并对各个残损参数对结构频率的影响进行敏感性分析。

1 结构概况

本文所研究的硬山古建筑为北京某四合院内的正房,始建于清朝末年。其平面形式为五开间布局,结构形式为典型的六檩前出廊硬山建筑,开间12m,进深4.3m,建筑平面图和剖面图分别如图1和图2所示。该建筑山柱位于山墙内,外部不可见;后檐金柱位于后檐墙内,外部仅后檐金柱柱头可见;前檐金柱嵌有槛墙。墙体均为围护墙体,其中山墙、后檐墙均为青砖垒砌。

图1 建筑平面图

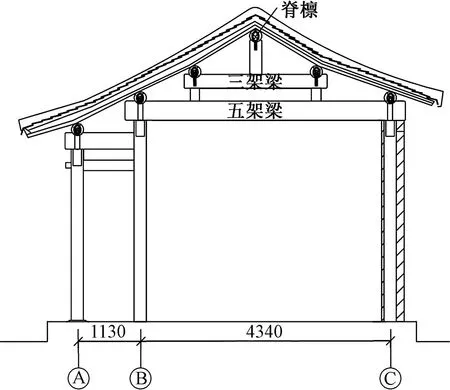
图2 1-1剖面图

2 现场无损检测

2.1 外观缺陷检查

由于结构已经过了上百年的服役,在长期自然环境的作用下,构件出现了不同程度的损伤,如梁枋开裂、柱表面腐朽、屋面破损等,如图3所示。

图3 构件破损现象

2.2 应力波检测

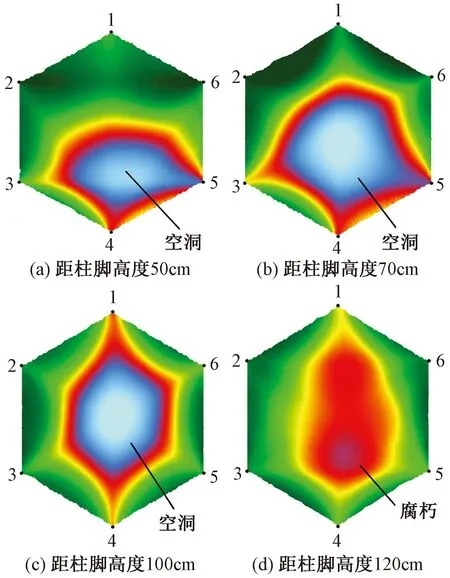
图4 柱3/A检测结果

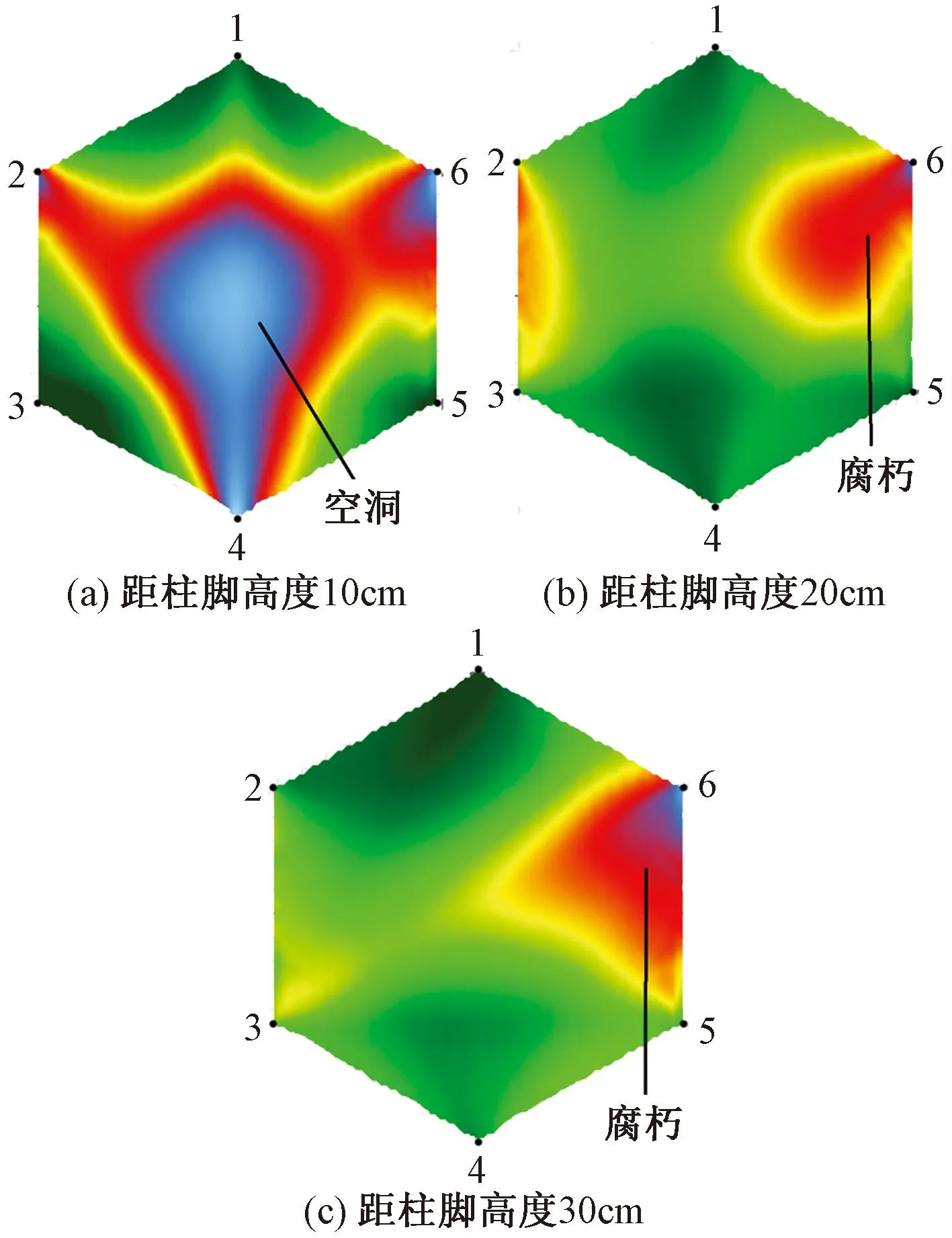
图5 柱4/A检测结果

2.3 微钻阻力仪检测

柱1/A、柱6/A和柱1/B～6/B共8根柱均有一半包裹在墙体中,一半露在外面。应用微钻阻力仪在8根柱的不同高度对其内部状况进行了检测,其中柱1/A和6/B的内部腐朽较为严重,其阻力曲线分别如图6和图7所示。柱的直径均为200mm,根据检测结果,柱1/A的最大腐朽面积位于距柱脚高度20cm处,距柱表皮80mm以后严重腐朽,腐朽面积随柱高度逐渐减小,腐朽的最大高度为100cm。柱6/B的最大腐朽面积位于距柱脚高度10cm处,距柱表皮100mm以后严重腐朽,腐朽面积随柱高度逐渐减小,腐朽的最大高度为60cm。其余6根柱内部结构较为完整,其中柱2/B的阻力曲线如图8所示,柱内未见明显腐朽。

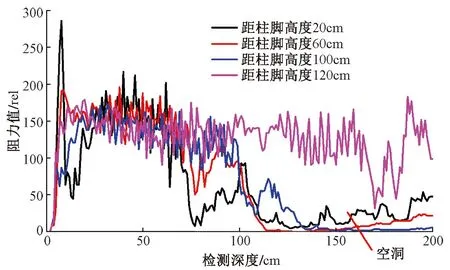
图6 柱1/A检测结果

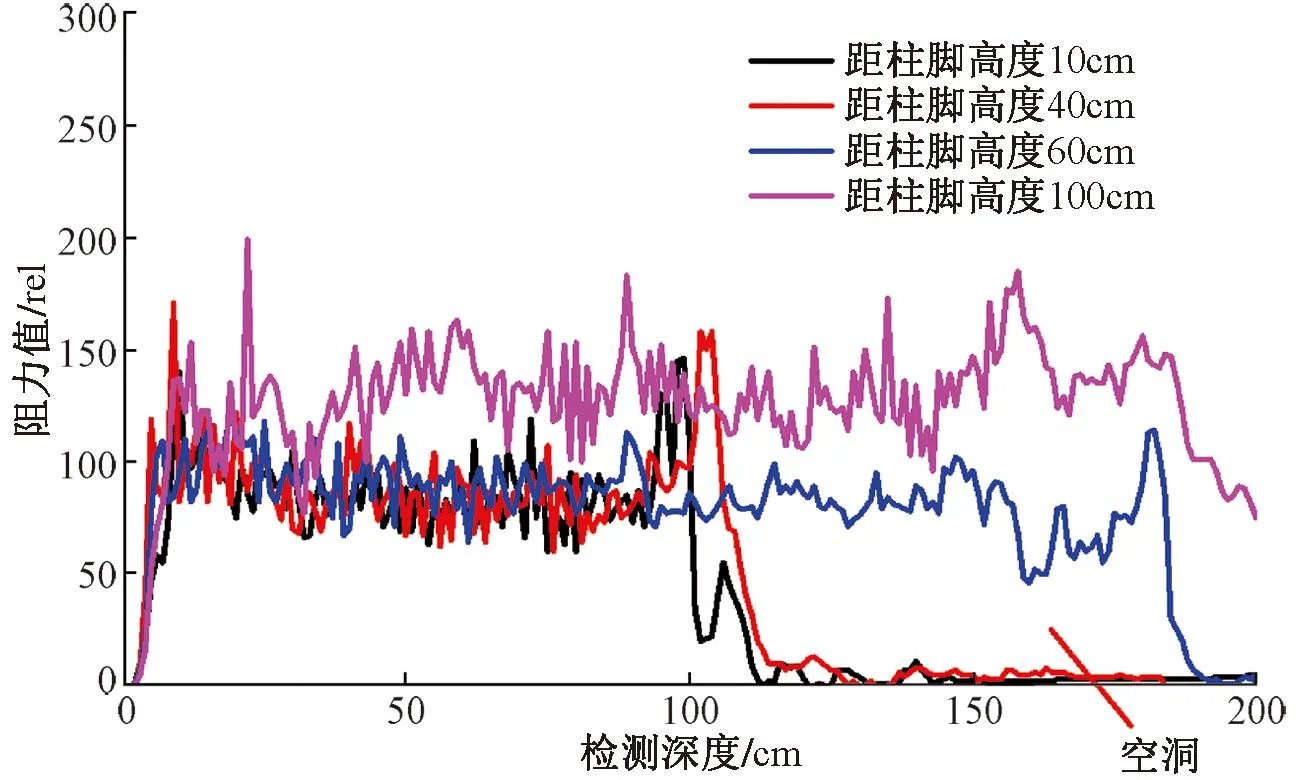
图7 柱6/B检测结果

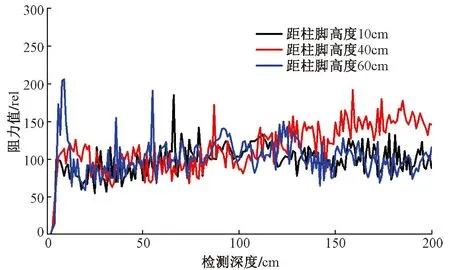
图8 柱2/B检测结果

2.4 柱倾斜检测

古建筑木结构在建造过程中柱子均会设置侧脚,在长期自然环境和屋顶荷载的作用下,柱子的倾斜角度会发生变化。应用全站仪对轴和轴的12根柱子的倾斜进行了测量,各柱在不同方向均有倾斜,其角度见表1。由于侧脚的缘故,12根柱整体向北倾斜,东、西方向倾斜的角度比南、北方向小。其中柱3/B倾斜角度最大,该柱向西倾斜0.15°,向北倾斜0.93°。

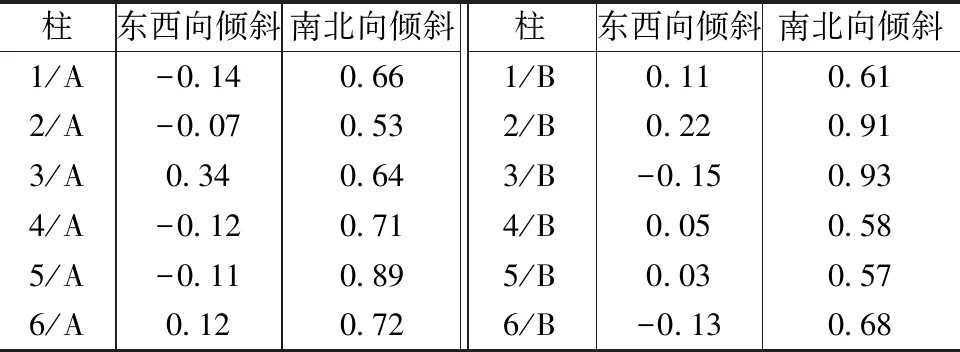
表1 柱倾斜角度/°

2.5 木材树种鉴定

根据现场情况,分别从柱4/A、④轴五架梁、 (2～3)/B下金檩选取了三组木材试样送实验室进行树种鉴定,其中下金檩的试样如图9所示。树种鉴定的依据标准为《木材鉴别方法通则》(GB/T 29894—2013)[17],鉴定结果显示,三处位置的木材均为硬木松,属松科松属。

图9 树种鉴定试样

3 有限元分析

3.1 模型建立

采用MIDAS Gen有限元软件,分别建立完好和残损的硬山式结构有限元模型,完好模型如图10所示。残损模型主要考虑柱倾斜、柱内部腐朽、材料老化等因素。完好模型的柱倾斜按照初始侧脚为1/100考虑,残损模型的柱倾斜按照实际倾斜角度考虑。残损模型的柱内部腐朽通过截面面积折减实现,根据无损检测结果,柱1/A、柱3/A的截面面积在柱高120cm以下折减1/2,柱4/A的截面面积在柱高30cm以下折减1/2,柱6/B的截面面积在柱高60cm以下柱折减1/2。Ⓒ轴的柱均嵌入在山墙中无法检测,而墙内的柱易发生腐朽,因此残损模型中将Ⓒ轴的6根柱均假定1.2m高度以下截面面积折减1/2。

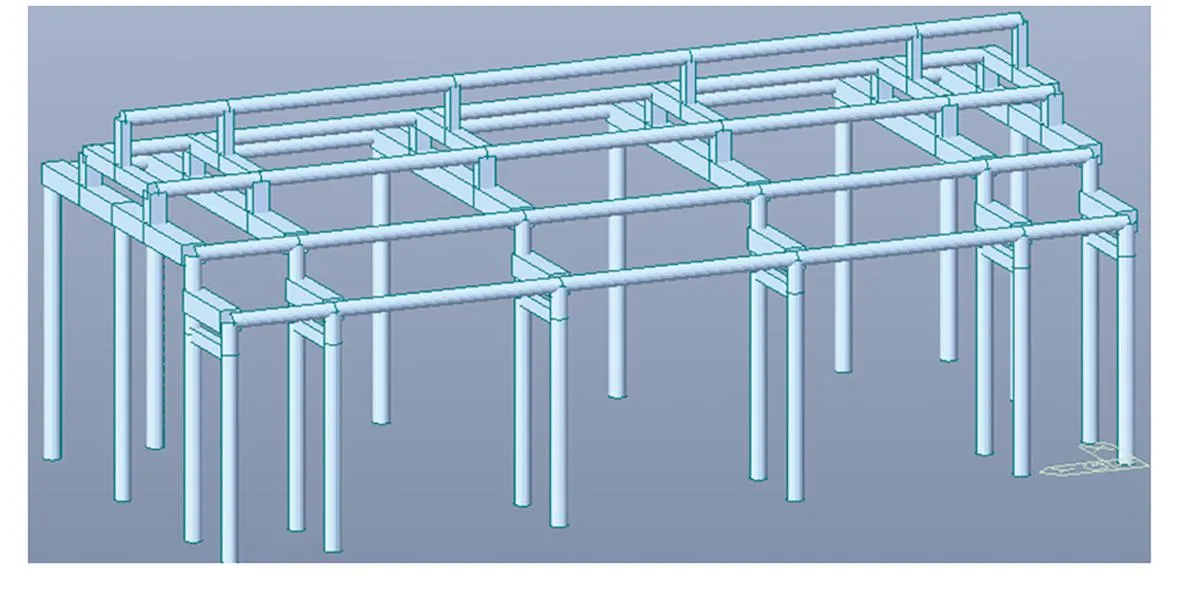
图10 完好结构有限元模型

3.1.1 材料参数

根据树种鉴定结果,该古建筑主要用材为硬木松。根据《木结构设计标准》(GB 50005—2017)[18],完好模型的材料参数取值见表2,EL、ER、ET分别为木材顺纹、径向和切向的弹性模量,GTR、GLT、GRT分别为径向和切向、纵向和切向、纵向和径向三个切面的剪切模量,σc为抗弯强度,σb为顺纹抗压强度,σt为顺纹抗拉强度。对于残损结构,根据《古建筑结构安全性鉴定技术规范 第1部分:木结构》(DB11/T 1190.1—2015)[19],计算古建筑木结构时,其木材设计强度和弹性模量应乘以重要性系数0.9;对于木质老化构件,应乘以考虑长期荷载作用和木质老化的调整系数0.9。因此,对残损模型的材料参数进行81%的折减。

表2 完好模型材料参数取值/MPa

3.1.2 荷载取值

结构的恒载主要为屋面自重,根据现场勘查的屋面构造做法,参照《古建筑屋面荷载编汇》[20]计算屋面各部分的质量,如表3所示,屋面的总质量为146262kg。根据《古建筑木结构维护与加固技术标准》(GB/T 50165—2020)[21],屋面活荷载取0.7kN/m2,基本风压为0.6 kN/m2,基本雪压为0.48 kN/m2。考虑荷载组合后,计算模型中将各种荷载均以线荷载的形式平均施加在屋架的每个檩上。

表3 屋面各部分质量/kg

3.1.3 关键节点简化

本结构中的关键节点包括榫卯和柱脚节点,建立有限元模型时应合理的设置节点刚度以反映节点对整体受力的影响。

榫卯节点表现出的的受力特征是半刚性连接,即节点具有一定的拉压和转动刚度。拉压刚度只考虑梁长度方向的拉压刚度K1;扭转刚度不考虑梁绕自身轴的扭转变形,假设另外两个方向抗弯刚度相同,记为K2。根据已有的有限元模拟和试验研究结果,取榫卯的刚度为:K1=250kN/m[16],K2=335.88kN·m/rad[22]。

在古建筑木结构中,柱脚浮搁在柱础石上,在结构底部承担着传递竖向和水平荷载的作用。在水平荷载作用下柱脚截面会出现不均匀的的嵌压以提供恢复力,因此柱脚是具有一定抗弯刚度的半刚性节点。根据已有的试验结果,柱脚的抗弯刚度取值为:K3=426.5kN·m/rad[23]。

对于残损结构,考虑材料退化、材料残损等因素,参照材料参数的折减系数,其K1、K2、K3的取值均进行81%的折减。

3.2 模态分析

分别对完好模型和残损模型进行模态分析,前三阶自振频率的结果见表4,完好模型的振型结果见图11。可见,第一阶振型为东西向平动,第二阶振型为南北向平动,第三阶振型为扭转。

表4 前三阶自振频率/Hz

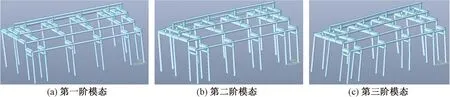
图11 完好结构的前三阶振型

参照《古建筑防工业振动技术规范》(GB/T 50452—2008)[24],古建筑木结构的水平固有频率fi计算公式为:

(1)

式中:H为结构计算总高度,H=3.28m;λj为结构第j阶频率计算系数,λ1=1.571;ψ为木结构质量刚度系数,按照无围护墙取ψ=33。

根据计算公式(式(1)),结构的第一阶频率计算值f1=2.51Hz,计算值和完好模型模拟值的误差为1.2%,误差较小,可以验证计算模型的可靠性。

由表4的频率对比结果可知:残损模型的各阶频率均比完好模型低,前三阶频率分别降低了13.7%、14.1%、12.7%,说明结构缺陷、材料退化等残损因素降低了结构的整体刚度,影响了结构的动力特性。

3.3 结构静力分析

静力分析中考虑的荷载为恒荷载、活荷载、风荷载和雪荷载,根据《建筑结构荷载规范》(GB 50009—2012)的规定,不上人的屋面活荷载可不与雪荷载和风荷载同时组合。本结构可视为由永久荷载控制,经验算,内力最大的荷载组合形式为:1.35恒荷载+1.4×0.7活荷载。

完好模型和残损模型部分构件的最大应力对比见表5,其中柱为顺纹受压应力,梁为受弯应力。由表5的对比可知,残损模型中梁、柱的最大应力均高于完好模型,这是由于截面削弱、材料退化等因素引起的。

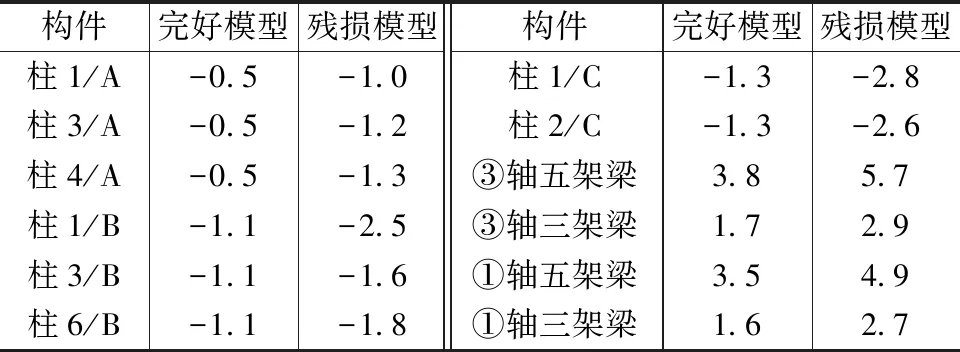
表5 构件最大应力对比/MPa

3.4 结构地震响应分析

地震响应分析时选取了Taft波、天津波和El Centro波作为地震激励。根据《建筑抗震设计规范》(GB 50011—2010)[25],北京地区抗震设防烈度为8度,设计基本地震加速度值为0.2g,将地震加速度最大值按70cm/s2对每条地震波进行调幅,作用于完好模型和残损模型进行时程分析,分别计算两种结构东西向和南北向的地震响应。

3条地震波作用下完好模型和残损模型结构脊檩处的最大加速度、最大位移和最大位移角见表6。从表6中可以看出:1)对于完好模型或残损模型,在不同地震波作用下其最大加速度、最大位移和柱头位移角均差别较大;2)相同地震作用下,残损模型的最大加速度、最大位移和柱头转角均大于完好模型,说明残损因素会进一步增大结构的地震响应;3)计算结果中东西向的最大加速度、最大位移和最大位移角均大于南北向,说明东西向的刚度小于南北向,与模态分析的结果一致;4)根据《古建筑木结构维护与加固技术标准》(GB/T 50165—2020),抗震变形验算中木构架的位移角限值可取1/30,对应的角度为1.9°,完好模型和残损模型的抗震能力满足要求。

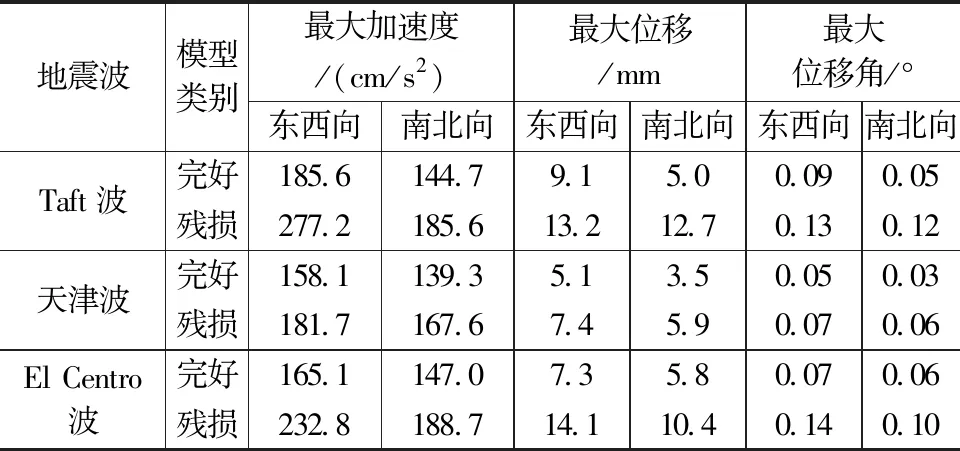
表6 最大加速度、最大位移和最大位移角

3.5 残损参数对结构频率的敏感性分析

材料退化、节点刚度降低等残损因素均会影响结构的频率,且各个参数对结构频率的影响程度各不相同。参数的敏感性分析有助于识别关键参数,减少参数的不确定性影响。影响结构频率的主要残损参数有:材料顺纹弹性模量EL、榫卯拉压刚度K1、榫卯抗弯刚度K2、柱脚抗弯刚度K3,将各个参数的取值在一定合理范围内变化,计算结构频率对各参数的敏感性。

Morris方法[26-28]是一种常用的敏感性分析方法,其原理是选取模型中的一个变量Xi,其余参数值固定不变,自变量Xi以设定好的变幅变化运行模型得到目标函数y(x)=y(X1,X2,…,Xn)的值,用影响值Si判断参数变化对输出值的影响程度。

(2)

(3)

式中:yi为参数变化后的输出值;y0为参数变化前的输出值;X0为初始参数值;Δi为参数变化的幅度。

灵敏度判别因子S取Si的平均值,即:

(4)

设定木材顺纹弹性模量EL的取值范围为5 000～12 000MPa,K1的取值范围为0～600kN/m,K2的取值范围为0～1 000kN·m/rad,K3的取值范围为0～1 000kN·m/rad。结构第一阶频率随各参数变化的曲线如图12所示,结构频率和各参数之间均成正比。根据Morris方法,计算得到各参数对第一阶频率的灵敏度判别因子的结果见表7。结果表明:结构频率对4个残损参数的敏感性排序为:EL>K3>K2>K1,木材的顺纹弹性模量对结构频率的影响最大,榫卯的拉压刚度对频率的影响最小,且柱脚节点比榫卯节点对结构频率的影响更大,在日常维护中应更加关注柱脚的残损。

表7 各参数的灵敏度判别因子S

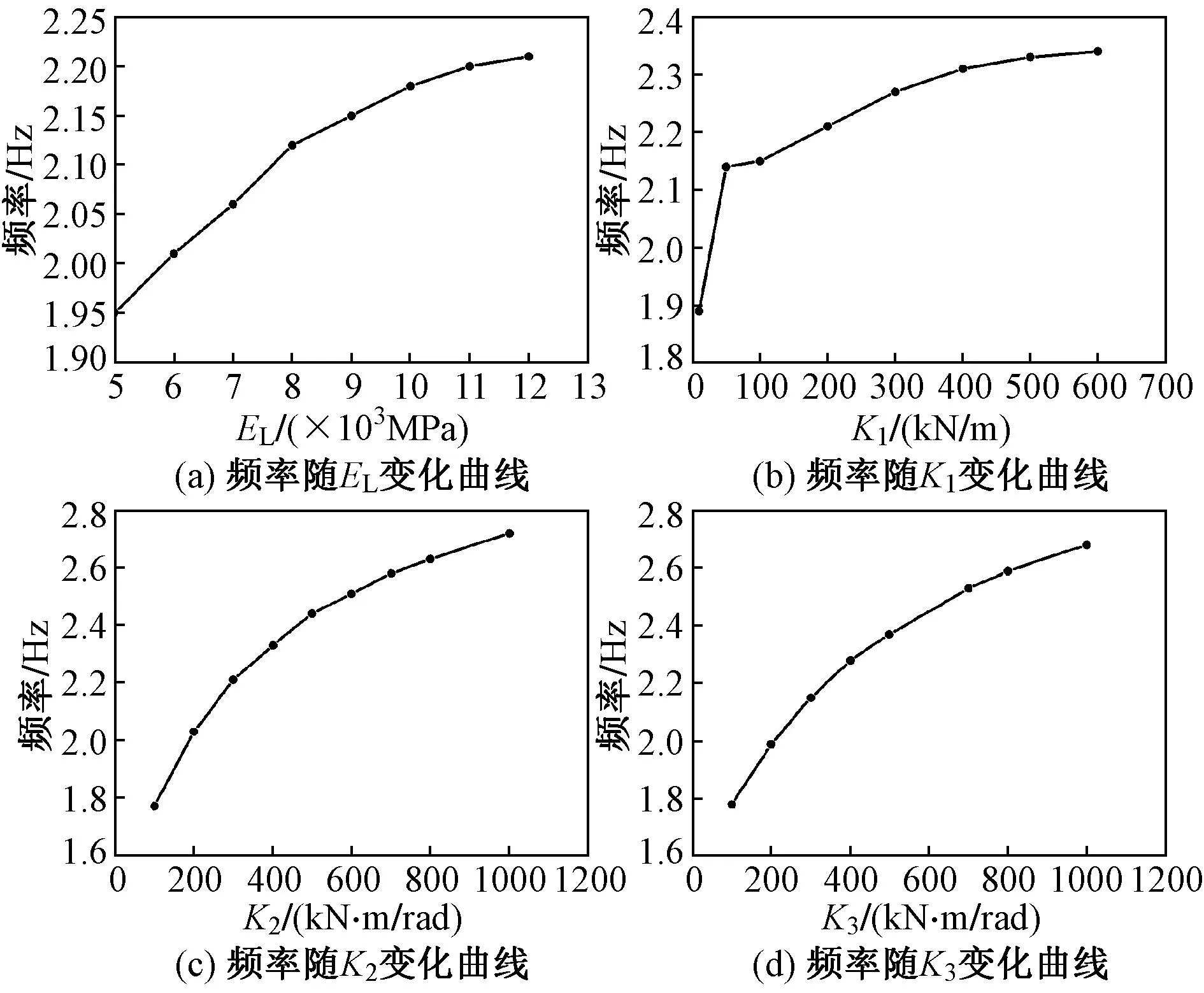
图12 第一阶频率随残损参数的变化曲线

4 结论

(1)通过无损检测确定了硬山式古建筑木构件的内部残损、柱倾斜等,木柱内部的最大腐朽面积超过了柱截面的1/2。

(2)基于检测结果建立了结构的完好模型和残损模型,并通过频率结果对有限元模型的有效性进行了验证。结构中存在的残损现象削弱了结构刚度,残损模型的各阶频率明显低于完好模型,前三阶频率分别降低了13.7%、14.1%、12.7%。

(3)在静力作用下,受残损现象的影响,残损模型中梁、柱的最大应力均高于完好模型。

(4)结构在不同地震波作用下,地震响应均不同;在相同地震波作用下,残损模型的地震响应均大于完好模型。

(5)根据敏感性分析结果,在各残损参数中,材料的顺纹弹性模量对结构频率的影响最大,榫卯的拉压刚度对结构频率的影响最小,柱脚节点比榫卯节点对结构频率的影响大。