基于基准网稳定性检验的自动化监测系统研究

马彦凤，常梦雅，樊海青，肖 红

（1. 广东省测绘工程有限公司，广东 广州 510700；2. 广东省国土资源测绘院，广东 广州 510700）

深基坑工程由于自身风险性较高，需布设大量监测点对其进行高密度监测作业，导致传统人工监测工作量较大、效率较低，且很难对基坑施工引发的安全问题进行及时反馈[1]，因此基于测量机器人的基坑三维形变自动化监测系统应运而生。基坑自动化监测系统能实时获取基坑变形信息，并自动上传至云端[2]，无需人工干预，具有较高的时效性和量测便捷性。现阶段，已有较多自动化监测系统应用到基坑工程项目监测中，但大多未与施工工况进行有效结合，设站点变形对监测结果影响较大[3]，且未对该影响进行校验修正，也未考虑气象条件和施工环境对监测数据的影响[4]，自动化监测成果可靠性较差。本文从现有基坑自动化监测系统的不足出发，设计了顾及基准网稳定性检验的优化算法，对气象环境参数未知条件下的监测数据进行了差分改正，并通过实验和项目应用进行精度验证。结果表明，优化后的自动化监测系统监测数据精度显著提升，可为基坑施工安全提供准确可靠的数据支撑。

1 基准网稳定性检验

1.1 平均间隙法原理

三维形变自动化监测系统通常以测量机器人为核心设备，采用极坐标法测量原理[5]，但当设站点或后视基准点发生变形时，往往无法自动识别，从而导致监测数据可靠性降低，影响施工安全判断。为解决该问题，本文采用平均间隙法对基准网稳定性进行检核。平均间隙法主要包括整体检验和局部检验，整体检验是检测基准网中是否存在动点，局部检验是确定动点位置。平均间隙法的基本思路为：将两个等精度观测周期的基准点坐标值作为一组双观测值，利用双观测值之差计算观测值的单位权方差验后估值；再对两个观测周期图形进行一致性检验[6]，判断是否存在动点，如存在，则依次去掉一个基准点；然后计算两个观测周期图形差异性降低的程度，降低最大的点则为动点[7]；重复上述过程，直至所有动点均被剔除为止。

1.2 基准网动点检查

假设i、j为两个观测周期的等精度监测数据，利用平差改正数获取其单位权方差的估值，则有：

式中，、分别为i、j的单位权方差验后估值；σ2为联合单位权方差估值；v为观测值的改正数；p为观测值的权矩阵；fi、fj分别为i、j的自由度。

假设两个观测周期的基准网无动点，利用两期基准点坐标差计算另一方差估值，即

式中， ΔX为两期基准点坐标差；θ2为方差估值；PΔX=QΔX-1=(QXj+QXi）-1；fΔX为独立个数。

对σ2和θ2进行F检验，如式（3）所示，检验是否存在动点。

原假设H0为两期观测的基准网无动点，统计量F则服从自由度为fΔX、f的F分布，则有：

式中，α为置信水平，取值通常为0.05 或0.01；分位值F1-α(fΔX'f) 可从F分布表中查找获取，若F＜F1-α(fΔX'f)，则H0成立，基准网无动点，反之，则拒绝H0，基准网中存在动点。

1.3 基准网动点定位

当整体检验发现基准网中存在动点时，可采用间隙分块法对动点进行精确定位[8]。将基准网中的基准点随机分为稳定点组M和不稳定点组N，采用图形一致性检验法对M进行动点检查，若无动点，则再对N进行检查。将ΔX、PΔX按照M和N进行排序并分块，即

由于ΔXM和ΔXN相关，则PMN=≠0，且受N影响，PMMΔXM无法检验M图形一致性，因此需要对其进行转换，则有：

ΔXMΔXM能对M的图形一致性进行准确表达，因此其方差估值为：

对M进行稳定性检验，其统计量的计算公式为：

原假设H1为M中无动点存在，则有：

若F1＜Fα(fF'f1+f2)，表示H1成立，M中无动点；反之，则拒绝H1，M中存在动点，需对其再次分组检测，分离出稳定点组。此时，除N外，其他基准点均为稳定点，但N中可能存在多个动点，需对其进行逐个搜索，排查出一个动点后，再对剩余的基准点进行稳定性检验，直至剩余基准点无动点为止。

若基准网中的不稳定点为后视基准点，则进行剔除，后续观测过程中同步观测不稳定的基准点，将其视为监测点归入基准网扩展网，采用经典平差方法对其进行平差计算，多次监测稳定后再作为新的后视基准点存储[9]；若不稳定点为测量机器人设站点，则采用间接平差方法重新计算设站点三维坐标，在系统内自动更新。

1.4 基准网校核实验验证

为验证平均间隙法基准网校核算法的可靠性，本文在稳定区域内设计动点测试实验，采用测角精度为0.5″ 、测距精度为0.8 mm+1 ppm 的高精度SOKKIA NET05AXⅡ测量机器人进行测量实验，设站点、后视基准点和监测点均采用强制对中装置降低对中误差，后视基准点和设站点均安置具有精密刻度的可微调整平基座，便于控制点位位移。本次实验在多云无风天气下进行，分别仅移动后视基准点、仅移动设站点、同时移动后视基准点和设站点，对比分析基准网校核前后各个监测点相对真值的变化情况，结果见表1，可以看出：①后视基准点发生位移变形时，基准网校核后监测点平差结果与真值之差均在1 mm以内，基准网校核前监测点存在一定程度的变化，但相较于后视基准点自身的变形值，监测点变形较小，但仍超过规范限差要求；②设站点发生位移变形时，基准网校核后监测点平差结果与真值之差也在1 mm以内，基准网校核前设站点发生位移对监测点的影响与设站点自身变形值基本一致，监测点误差较大；③后视基准点和设站点同时发生位移变形时，基准网校核后监测点坐标值与真值基本一致，最大差值仅为-0.3 mm，基准网校核前监测点误差与设站点变形值较接近。

表1 后视基准点和设站点变形校核前后数据变化分析

因此，相对于后视基准点，设站点位移变形对监测结果的影响更大，但后视基准点变形对监测结果的影响同样不可忽视；采用平均间隙法可以有效识别监测基准网中的动点，并对其进行修正处理，从而降低基准点变形对监测结果的影响，最大程度地保障监测数据的可靠性和准确性。

2 环境因素误差差分改正

测量机器人自动化监测过程易受大气折光、温湿度、大气压等环境因素影响，且多安装在露天环境下，采用厚度3 mm 的亚克力透明罩进行防雨防尘；但透明板材会对测量机器人激光束传播路径产生影响，随板材受损程度加重误差影响也会变化，且该误差属于动态未知环境变量，无法利用传感器获取。因此，本文采用固定参考基准差分改正方法对环境误差影响进行实时改正。

2.1 固定参考基准差分改正

在基坑三维形变自动化监测系统中，后视基准点、设站点和形变监测点共同构成监测基准网，由于测量机器人测速较快，在同一监测轮次内气象环境因素相对稳定，可将其视为不变量，以固定参考基准对监测结果进行实时差分改正[10]。同一监测轮次内测得的后视基准点和监测点数据均存在气象和环境误差，但后视基准点为已知监测基准，假定已知数据不存在误差[11]。因此，自动化监测前先测量后视基准点，并将实测的斜距、高差和水平角与已知数据作差，求出该测量轮次单位尺度下的斜距、高差和水平角改正数，从而对每个监测点的测量结果进行差分改正。

1）斜距差分改正的计算公式为：

式中，ds为该监测轮次下单位长度斜距差分改正数；为设站点和后视基准点间的已知固定斜距；SJ、Si分别为该监测轮次下测量机器人对后视基准点和某监测点的实测斜距；为该监测轮次下利用ds对Si进行差分改正后的监测点斜距。

2）高差差分改正的计算公式为：

式中，dh为该监测轮次下单位距离高差差分改正数；为设站点到后视基准点之间的已知固定高差；hJ为该监测轮次下设站点与后视点的实测高差；hi为该监测轮次下测量机器人对某监测点的实测高差；为该监测轮次下利用dh对hi进行差分改正后的监测点高差。

3）水平角差分改正的计算公式为：

式中，ΔL为该监测轮次下水平角差分改正数；LJ0为设站点与后视基准点之间的已知固定水平角；LJ为该监测轮次下设站点与后视点的实测水平角；LP为该监测轮次下测量机器人对某监测点的实测水平角；L'P为该监测轮次下利用ΔL对LP修正后的监测点水平角。

2.2 差分改正实验验证

为验证固定参考基准差分改正的可行性，本文在空旷具有硬化地面的室外场地内进行实验验证，布设1个设站点（CZD）、1个后视基准点（HSD）和1个监测点（JCD），均浇筑混凝土观测墩，采用强制对中盘降低对中误差[12]，设计3 种实验方案模拟高温和光线折射环境，在多云无风天气下选用SOKKIA NET05AXⅡ测量机器人对实验点进行多次重复观测，统计测量数据。

方案一：理想测量环境，光照和环境温度均不做改变，在多云无风天气条件下对后视基准点和监测点进行多次重复测量；方案二：高温测量环境，在测量机器人和实验点旁边放置小太阳取暖器，提高测量过程中的环境温度，对基准点和监测点进行多次重复观测，研究高温环境对监测结果的影响；方案三：折光测量环境，采用透明亚克力罩遮住测量机器人，模拟监测过程中增设透明保护罩环境，研究激光束传播速度和传播途径的改变对监测结果的影响。3 种方案的实验原始测量数据见表2，CZD与HSD之间的已知斜距、高差、水平角分别为58.357 5 m、4.286 6 m和104°35′32.21″；CZD与JCD之间的已知斜距、高差、水平角分别为24.859 4 m、3.741 5 m和104°35′32.21″ ，可以看出，方案一为理想测量环境，连续5轮测量结果变化较小，与各实验点已知数据的差值较小，最大斜距、高差、水平角差异分别为0.3 mm、0.4 mm和-0.27″ ；方案二改变了测量环境温度，测量结果与已知数据差异较明显，最大斜距、高差、水平角差异分别为-10 mm、-11.8 mm和-0.93″ ；方案三增设了透明防护罩，导致测量机器人激光束传播过程发生变化，测量结果与已知数据偏差较大，最大斜距、高差、水平角差异分别为-10.6 mm、-8.2 mm和-1.17″。

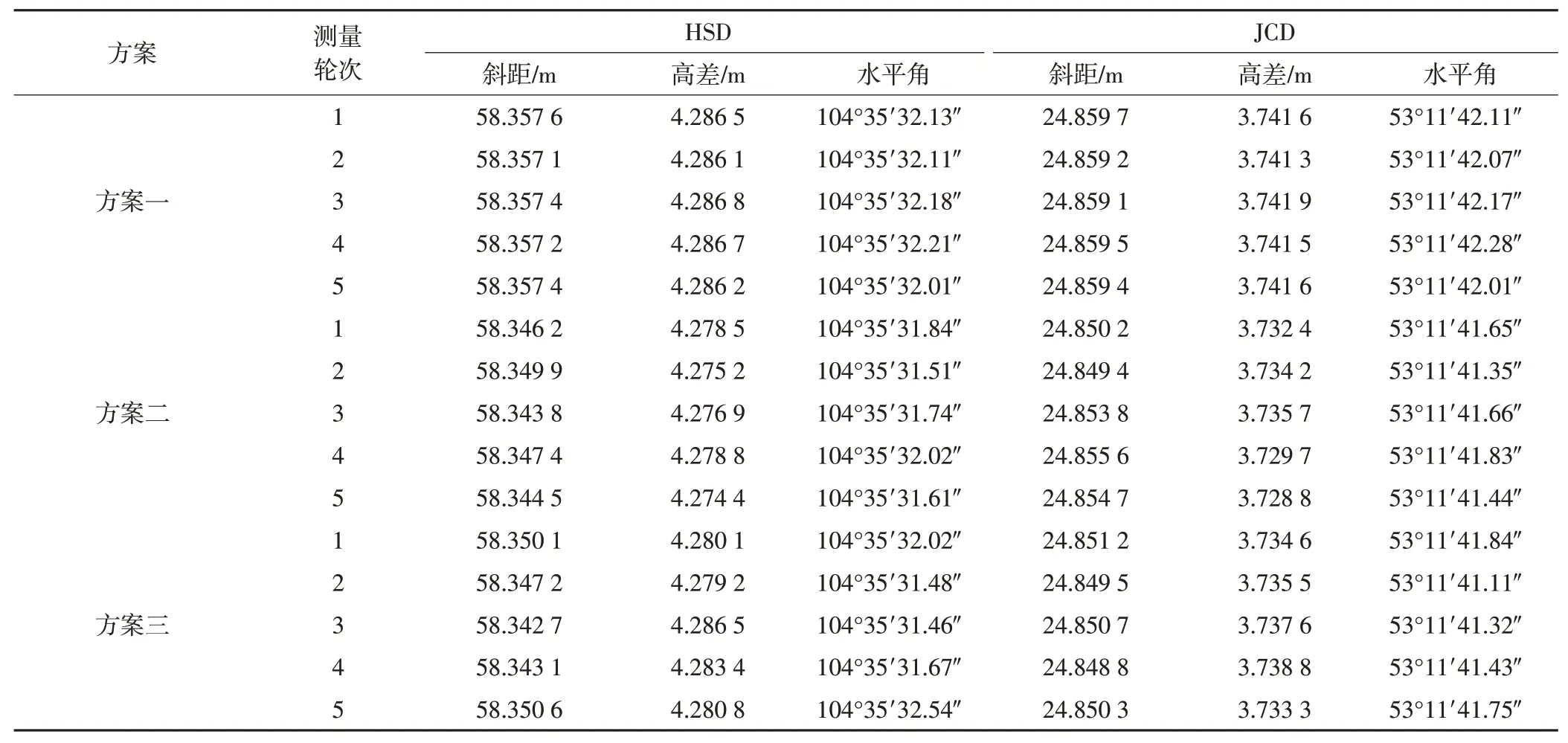
表2 差分改正实验原始测量数据

受限于实验场地面积，设站点、后视点和监测点之间的距离较近，但方案二和方案三的测量结果仍产生了较大偏差，说明温度和透明挡板会对测量结果造成较大影响，在自动化监测过程中不可忽视气象和环境因素的影响，需对其进行修正处理。本次实验采用固定参考基准差分改正方法对方案二和方案三中的JCD 数据进行差分改正，以方案一中较理想条件下的监测数据为数据基准，分别计算方案二和方案三差分修正后的斜距、高差和水平角，并与修正前的数据进行对比（表3），可以看出，经过差分改正后，两种方案CZD 与JCD 之间5 轮观测数据的实测斜距和单向三角高差与已知数据的差值均小于0.5 mm，水平角较差均小于0.5"，观测数据的准确性和可靠性得到大幅提升，因此利用后视基准数据对每轮观测数据进行差分改正处理，能大大降低气象条件和环境因素的影响，削弱测量误差，提高监测精度。

表3 方案二和方案三差分改正前后数据对比

3 项目应用分析

3.1 项目概况

为验证平均间隙法基准网校核和固定参考基准差分改正算法应用于实际工程项目的可靠性，本文利用某基坑自动化监测项目进行分析研究。该项目为跨海隧道盾构始发井深基坑，基坑长度约为156 m，宽度约为46.2～58.5 m；基坑开挖深度约为28.4～40.1 m，基坑深度范围存在填石、淤泥、砂层和粘性土，采用地下连续墙和6～8 层钢筋混凝土内支撑的支护形式。由于基坑开挖深度较深，基坑安全等级为一级，且基坑位于海边，地质条件较差，附近多为堆场，在基坑可视范围内基本无长期稳定区域，若采用人工监测方法，监测频率较低，难以满足基坑变形信息实时监控需求；若采用常规三维形变自动化监测方法，则无法对后视基准网的位移变形进行实时校核，需采用人工监测方法从远处城市高等级基准点进行频繁联测，大大增加了监测工作量，降低了监测效率，因此项目采用本文优化后的测量机器人自动化监测系统对基坑围护结构顶三维形变进行实时监测，每次自动化监测前均对后视基准网进行稳定性检验，以保障监测数据的准确性。项目采用SOKKIA NET05AXⅡ测量机器人进行自动化监测，利用透明亚克力罩进行防护，在基坑主要风险点共布设17 个监测点，在3 倍基坑开挖深度范围外的稳定区域布设4 个后视基准点（图1）。本文在数据库中提取自动化监测系统差分改正前后的监测点原始测量数据，采用相同设备对监测点进行人工测量，取测量数据的多次算数平均值作为真值。

图1 测点分布示意图

3.2 监测数据分析

测量机器人自动化监测频率默认为2 h/轮，监测数据量较大，本文选取MWD-ZQS-11 监测点进行分析，将监测点差分改正前后的原始观测数据与真值进行对比（表4），测量机器人设站点与稳定性较高的HS1后视基准点之间的已知固定斜距、高差、水平角分别为408.741 6 m、3.651 7 m 和91°18′17.38″；测量机器人设站点与MWD-ZQS-11 监测点之间的已知固定斜距、高差、水平角分别为113.265 7 m、3.216 9 m和173°51′45.19″。

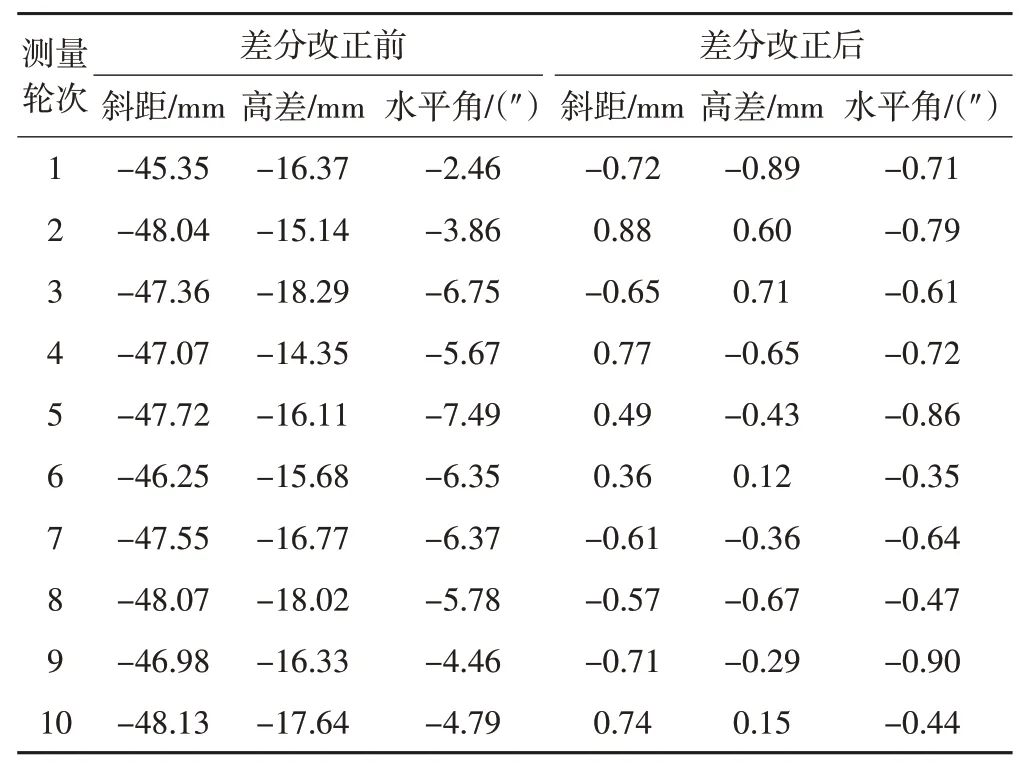
表4 差分改正前后与已知数据偏差

由表4 可知，差分改正前监测点原始观测数据与已知数据偏差较大，远超过实验数据的偏差值，主要是由于项目现场工况较复杂，影响监测结果的环境因素较多，且监测距离较远，导致差分改正前监测数据精度较差。在基于已知后视固定参考基准差分改正前，斜距、高程、水平角的观测最大偏差分别为-48.13 mm、-18.29mm和-7.49"，已超过项目监测预警值；差分改正后，监测数据精度得到了较大幅度的提升，斜距、高程、水平角的观测最大偏差分别为0.88 mm、-0.89 mm 和-0.90"，与已知数据偏差较小，监测结果较可靠，由此表明基于后视固定参考基准的差分改正算法能大幅降低温度、湿度、大气压、阴雨雾霾和透光板等外界环境因素对监测数据的影响，提高监测数据的可靠性，为深基坑工程施工安全提供数据支撑。

基坑施工过程中，采用人工校核方法每月对基准点进行复核，严格按照规范要求从城市高等级基准点进行控制点复核，结果表明控制网中一个基准点变化较明显，且设站点受施工影响一直在变动。将某一期基准网人工复核结果与自动化监测系统中基准网校核后的基准点和设站点数据进行对比，结果见表5，可以看出，测量机器人设站点SZD和基准点HS2均出现厘米级变形，变化较大，若不进行基准网检校则会使得监测数据出现较大变形，影响基坑施工安全分析；而采用本文设计的基准网校核方法，能够较准确地识别更新基准网中的动点，且检校成果与人工复核数据基本一致，说明采用平均间隙法进行基准网动态校核的实际应用效果较理想，能有效识别并校正监测过程中基准网变形，大大提高监测数据的精度。

表5 基准网校核成果分析/m

4 结 语

随着深基坑工程的大量涌现，传统人工监测难以实时获取基坑安全信息，基于测量机器人的自动化监测系统越来越成为深基坑实时监测的主要发展方向。本文分析研究了基坑自动化监测过程中基准网变形和外界环境因素对监测数据的影响，采用平均间隙法对监测基准网的动态变化进行检核，及时发现基准网变形并进行修正，保障监测过程中基准网的准确性；并基于已知固定参考基准对监测点数据进行实时差分改正，有效解决了气象参数未知条件下的气象和环境因素修正问题，提高了监测成果精度。通过设计相关实验验证了两种算法的可行性与可靠性，并成功应用于基坑自动化监测项目中，取得了较理想的应用效果，为基坑自动化监测系统稳定以及高精度数据获取提供了参考。