应用时空复合趋势面Kriging 方法插值地表沉降

黄丙湖，李欣芮，范芷睿，潘海燕，廖一兰

（1. 中国石油大学（华东） 海洋与空间信息学院，山东 青岛 266580；2. 新疆大学建筑工程学院，新疆 乌鲁木齐 830046；3. 中国科学院地理科学与资源研究所资源与环境国家重点实验室，北京 100101）

地铁施工中土质、荷载等因素将导致地面沉降，易引发坍塌、开裂等事故，因此必须建立相应的观测体系进行风险评估，以便采取相应措施防止事故灾害的发生。目前的常用方法为在地铁施工线上设立地表沉降监测点，并定期观测监测点沉降数据，但所得的采样数据较离散，无法直观体现整体沉降趋势，必须对采样数据进行插值[1-2]。空间插值考虑了沉降监测点在空间上的相关性，能对整体沉降区域的监测点进行预测。常用的空间插值方法包括几何方法、统计方法、函数方法和综合方法[3]，其中以Kriging 为代表的地学统计方法可定量描述空间随机分布变量的相关性，已应用于测绘、地质学、GIS 等学科，具有高度可行性和有效性[4-8]。陈雷[9]等利用Kriging 插值方法对地面沉降数据进行内插，但选取样本量小，只能反映局部趋势；刘志平[10]等利用Kriging插值方法研究了边坡变形速率，但其将变形速率演化为与时间相关的函数，弱化了时空关联性。在对地表沉降量等时空变量进行插值前，除分析变量空间相关性外，还应考虑时间相关性，王建民[11]等利用时空Kriging插值方法，将时间域扩展到空间域，建立了时空半变异函数，该方法计算量大，选择变异函数模型时需人工干预，会造成一定误差；Kyriakidis P C[12]等利用时空Kriging 插值方法研究区域变化量的时空分布特征，但未与传统地统计插值方法进行比较，无法体现其优势。时空复合趋势面（CSTM）兼顾了沉降点的时间相关性和空间相关性，利用已知沉降点监测值进行趋势面拟合得到区域内每个时空变量的全局平均趋势。因此，本文在传统地统计插值模型的基础上引入了CSTM，使模型能更准确地反映时空变量特征，从而提高模型预测精度；并与传统方法进行了精度对比，验证了时空插值的优势。

1 基于CSTM的Kriging插值方法

1.1 CSTM

CSTM 首先通过区域内已知时空变量的属性值进行趋势面拟合，再利用指数平滑法得到每个时空变量的属性值。该方法将区域内每个属性值分为趋势值和残差值两个部分，以此反映时空变量的变异情况。Lee[13]等提出CSTM 是基于时空随机场等理论定义的。时空随机场[14]即z(p)=z(s't)，包括时间尺度和空间尺度两个维度，s为二维空间位置（本文中为沉降监测点空间位置），t为时间（本文中为沉降监测点观测时间），将Y(p)=log[z(p)]作为z(p)的对数变换。全局平均趋势mY(p)是由Y(p) 构建的确定性函数，反映Y(p)的全局平均趋势。CSTM是基于复合时间/空间指标获得mY(p)的有效方法[13]。传统理论获得mY(p)（即mY(s't)）的方法是将其分为时间和空间两部分，而CSTM的优势在于兼顾了时间分量与空间分量[15]。

对于一个周期性变量，CSTM 可利用基于指数平滑函数的权重来计算拟合函数，以获得每个时空坐标平滑的平均趋势值，在任意时空坐标pj=(sj'tj)下，平均趋势值的计算公式为[13]：

式中，Y(sj'tj)为沉降量在可测量监测点pj处的对数变换；wi为权重；d(si'sj)为沉降监测点pi、pj之间的欧氏距离，；as、at分别为指数平滑函数的空间范围和时间范围。

1.2 基于CSTM的Kriging插值

CSTM 将区域内每个属性值分成趋势值和残差值，基于CSTM的Kriging插值是对残差进行插值，再与趋势值求和，最后得到时空变量的预测值。

1）数据空间分布的判断。使用Kriging 插值方法的前提是待插值数据满足正态分布且具有空间自相关性，因此可利用Moran’s I等空间自相关性统计量指标判定待插值数据的空间分布特征，满足该前提才能使用该方法。

2）时空尺度的确定。式（2）中as的选取原则为小于等于两个测量沉降监测点之间的最大欧氏距离，at的设置原则为小于等于沉降监测点多次观测的最大时间差。根据式（2）计算得到指数平滑函数的权重。

3）mY(p)的计算。沉降过程中根据已知监测点沉降量来构建CSTM，利用式（1）计算得到每个时空监测点的mY(p)。

4）Kriging插值。Y(p)由确定性变换X(p)=Y(p)-mY(p) 产生，由局部稳定平均值mx(p)=E[X(p)]=E[Y(p)-mY(p)]获得固有平稳时空随机场，其中E[.]表示期望算子[13]，X(p) 为残差。由于沉降监测点p=(s't)和p'=(s''t')之间空间滞后γ=‖s-s'‖ 和时间滞后τ=|t-t' |的影响产生误差，二者之间的总体误差用协方差计算，能衡量一对沉降监测点间的时空相关性，即

Kriging 插值方法考虑了样本之间的空间相关性，通过最小化均方误差权重来获得未监测沉降点残差的最佳估计值。X(p)在点k处的估计值⌒是测量值xd的线性组合，计算公式为：

式中，λ为采用传统Kriging 插值估算权重的列向量，沉降点pk、pd的时空复合距离越近，权重越大；mx(pk)、mx(pd)为X(p)在预测点pk、pd的平均趋势。

式中，cx(pk'pd)为估计点与数据点之间X(p)的协方差行向量；cx(pd'pd)为数据点之间X(p)的协方差矩阵[16]。

5）监测量插值结果的估计。将区域内每个沉降监测点的mY pj=(sj'tj) 与Kriging 插值得到的残差对应求和，最后进行指数变换得到每个监测点的沉降量。

2 实验与结果分析

2.1 数据来源

本文的实验数据来源于乌鲁木齐市轨道交通3 号线一期工程05标明园站—友好站区间，该工程处于施工阶段，以2 号竖井和横通道开挖。考虑到地层自稳能力差，受开挖、支护工程和地下水等因素影响，地表会出现不同程度沉降，因此竖井施工过程中针对可能沉降变化较大的区域布设41个监测点，构成了6条监测线（图1），在井口顶部圈梁短边周围布设6个监测点，其余监测点分别布设在竖井横通道附近和隧道线路附近。采用徕卡电子水准仪（±0.3 mm/km），按照二等水准测量方法，对地表监测点进行观测，经平差合格后，获得监测点处的高程；再统计观测期间监测点的高程变化情况，获得沉降变化量。实验获取了2017-06-24—2017-09-08 共15 期沉降数据，监测频率为5 d/次，监测过程中个别监测点数据缺失，导致总数据量小于n=41×15。

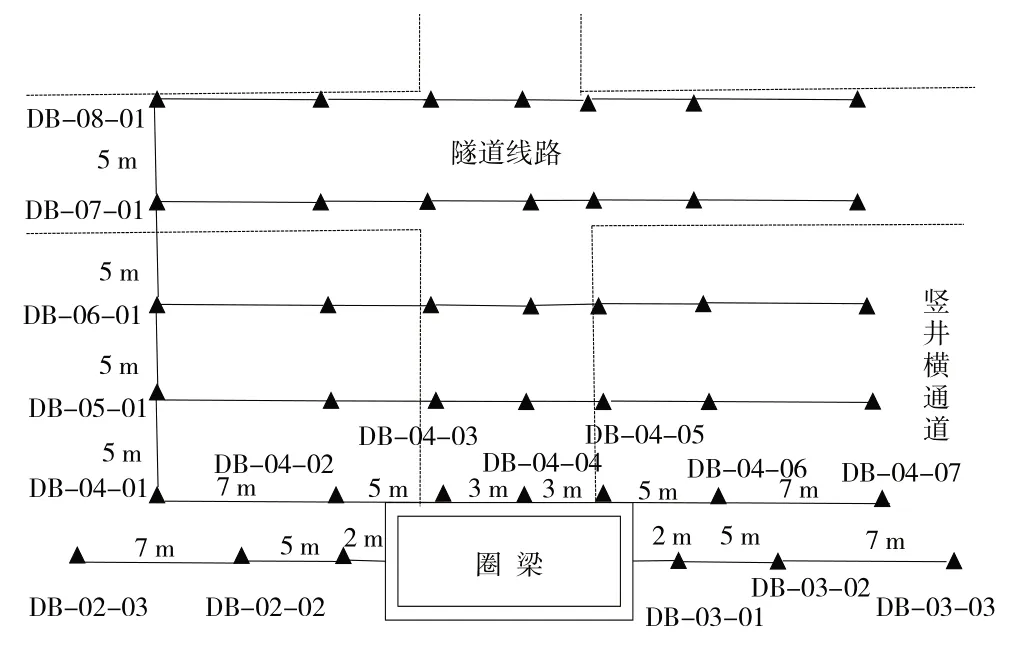
图1 地铁地表沉降监测点布设图

2.2 插值过程

首先，对获取的数据进行空间自相关性检验，利用Moran’s I 进行判定，p值小于0.05 且z 得分超过1.65，认为通过95%置信度检验，结果见表1，可以看出，4个时段的数据未通过显著性检验，且它们的Moran’s I 均接近于0，空间自相关性很弱，将其剔除。本文分别利用Kriging插值和基于CSTM的Kriging插值方法对研究区内符合条件的11个时段的监测点沉降量进行插值。实验中选取每期监测数据利用Kriging方法进行独立插值发现，预测沉降监测点与半径为2 m 区域内的已知沉降点空间相关性最强，因此确定CSTM基于指数平滑函数权重的空间尺度为2 m，时间尺度选取待插值数据的前后1 个时间段。值得注意的是，由于剔除了7 月30 日—8 月4 日的数据，导致该时段周期变为10 d，即7月30日—8月9日，本文将这种时段相距天数不相等的间隔称为非等时间间隔，反之称为等时间间隔。然后，计算区域内每个沉降监测点的mY(p)。最后，对每个地表沉降监测点的残差进行Kriging插值。

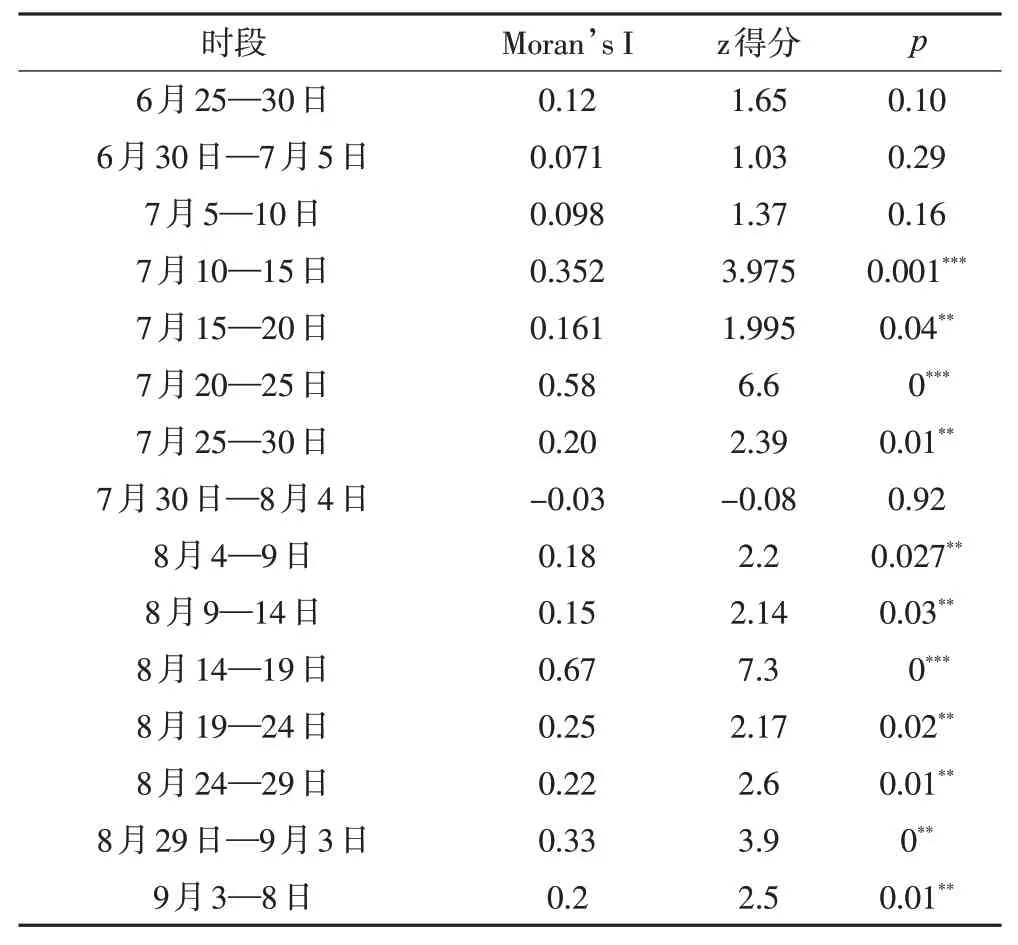
表1 实验数据空间自相关性检验

两种方法的插值结果见图2，可以看出，圈梁、竖井横通道附近的沉降程度相对明显，因此施工过程中需加强监测这两个部分；基于CSTM的Kriging插值方法考虑了时空相关性，7月15—25日圈梁附近地表缓慢下降，而7月25日—8月14日则开始抬升，后期逐步趋于稳定状态；竖井和横通道附近的点在不同时段内沉降波动较大，这可能是由施工推进造成的。

2.3 精度评价

实验采用留一交叉验证的方法，即对于N个样本，每次选择N-1 个样本训练数据，一个样本验证模型预测的好坏。该方法的优势在于，每个回合中几乎所有的沉降数据皆用于训练模型，因此最接近原始沉降数据的分布，评估结果比较可靠。首先假定某一监测点沉降量为未知，然后利用插值方法计算该监测点沉降量，最后计算该监测点实际观测值与插值得到的沉降值之间的误差。这种误差主要是由插值算法的准确性和监测点的分布情况造成的[17]。实验选取均方根误差（RMSE）和R2作为精度验证指标（表2），RMSE 可反映监测点数据插值结果的离散程度，计算公式为：

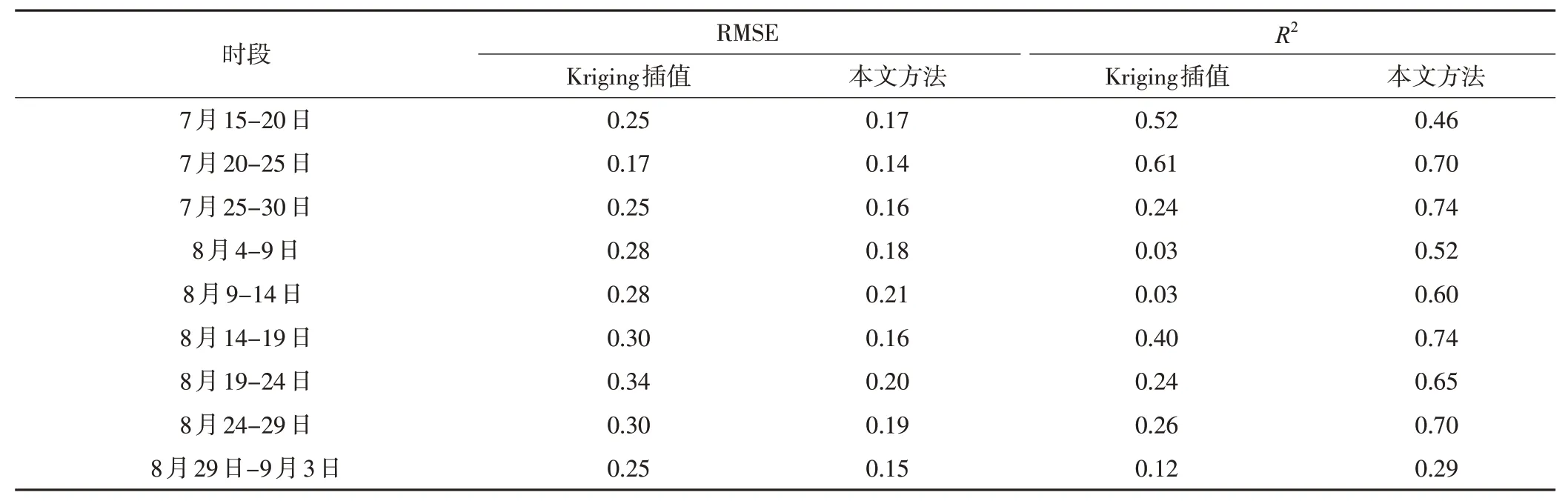
表2 两种方法的RMSE和R 2 比较

式中，vi为第i个监测点的实际沉降量；v'i为第i个监测点的差值估算值；n为参与交叉验证的监测点数目。

R2可体现模型的拟合效果，由残差平方和总体平方组成，其值越接近1，表明线性相关程度越高，计算公式为：

由表2 可知，空间插值和时空插值都表现出较强的线性相关性，本文方法比传统方法的RMSE 降低约35%，说明本文方法的总体离散程度明显小于传统方法；传统方法的R2大部分在0.5以下，而本文方法的拟合程度更好；综合来看，本文方法提高了模型精度，更适用于地表沉降监测。

然而，CSTM 未给出标准的时间尺度确定方法，因此本文在前后一个以非等间隔时间段为指数平滑的时间尺度实验之后，又将时间尺度设为等间隔时间段进行探索性实验，结果见表3，可以看出，采用等间隔时间段的沉降数据构建CSTM 得到的精度更好。插值结果见图3。

表3 不同时间尺度的本文方法的精度评价

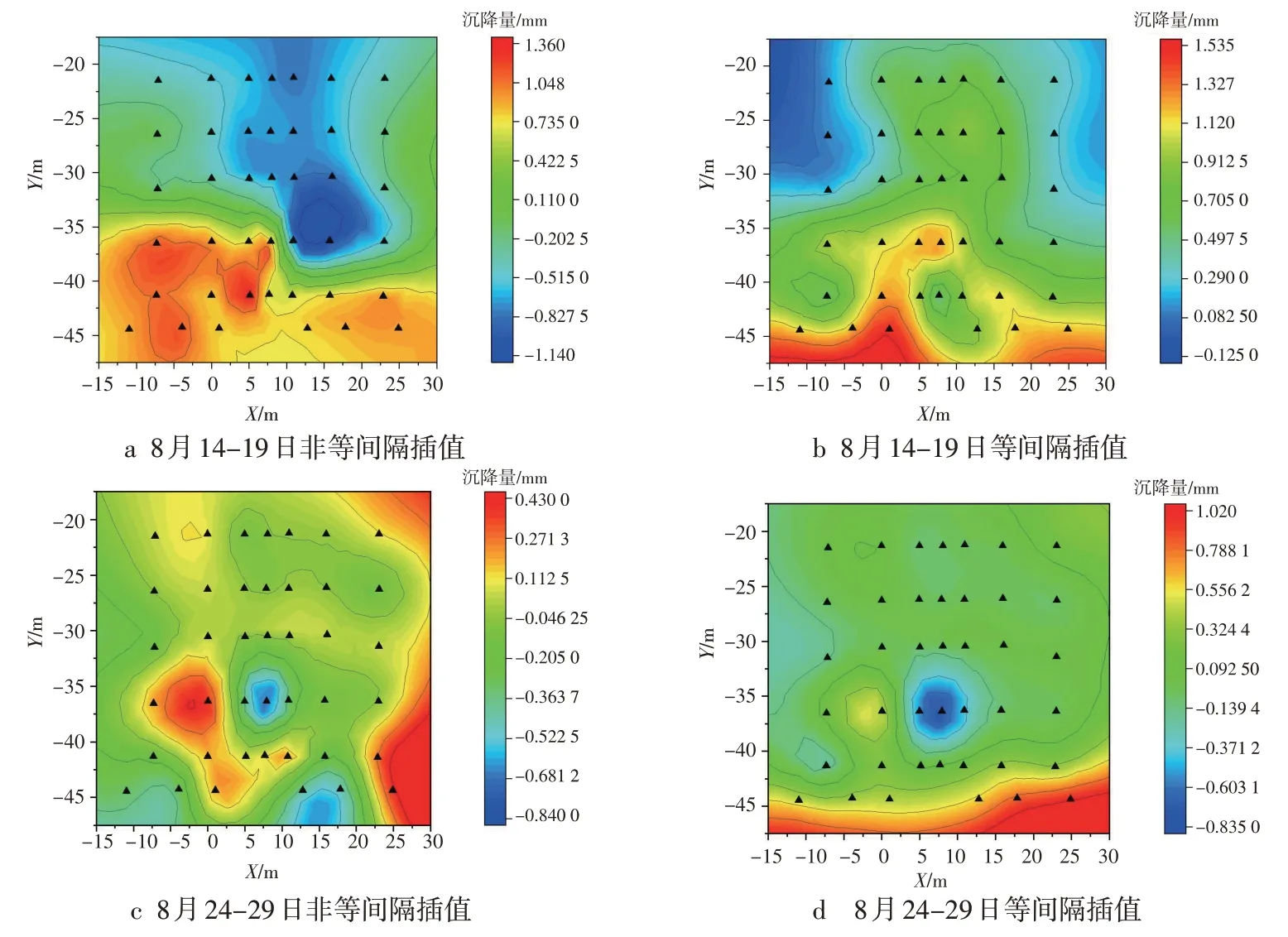
图3 同时期非等间隔与等间隔本文方法插值结果比较

CSTM 同时考虑了沉降监测点的时间相关性与空间相关性，因此选取研究区域内均匀时段进行预测将得到更好的效果，由于本次实验数据量的局限性，等间隔沉降量差值的时间序列较短，未来可选取更长时间序列进行实验。

3 结 语

本文将CSTM 引入Kriging 插值，同时考虑了空间相关性和时间相关性，使该插值方法能更真实地反映时空变量变化趋势，提高了地表沉降监测精度。实验表明，与传统方法相比，本文方法的RMSE 降低约35%，具有更高的拟合精度；从插值结果来看，能更精细地反映沉降量的时空差异，以实现对地铁地表沉降的有效监测。受限于数据观测天数较少，本文具有一定局限性，未来可考虑对更长时间的沉降监测进行实验，同时可引入周边建筑物、土质、施工方式、人口密度、车流量等辅助变量来优化插值模型，实现长时间、大范围的地表沉降趋势分析。除此之外，本文方法还可与三维激光扫描数据的点云数据相结合，对格网化后的点云数据进行插值，实现更高效快捷的整体监测分析。