基于双重限制Q 学习的机器人控制方法

周维庆，王飞，赵德京

（1.青岛大学 自动化学院，青岛 266071；2.山东省工业控制技术重点实验室，青岛 266071；3.山东潍坊烟草有限公司，潍坊 262400）

伴随着人工智能的兴起，强化学习在近些年得到了广泛的发展，但是强化学习的面向对象大多是虚拟环境，很难真正的应用到现实生活中，这是由于强化学习的训练需要智能体不断与环境交互，不仅成本高，安全性也得不到保障。为了解决上述问题，近几年在广大学者的不断探索中，离线强化学习算法应运而生，其不需要智能体与环境进行交互，直接通过给定的历史数据集即可训练出令人满意的效果，这种特性使得人工智能可以更好地应用到现实生活中。但是离线强化学习的缺点也显而易见，由于数据集是固定大小的，不可能包含环境中所有的状态-动作，当面临OOD 动作时，很有可能对动作的价值高估，造成外推误差，随着算法的迭代更新，误差值将越来越大，最终影响算法的性能。

为了缓解外推误差等问题，先前的方法通常是约束学习策略，使学习策略尽可能的接近行为策略[1]，这种方法的本质类似于模仿学习，一定程度上缓解了外推误差带来的影响，又或者是根据值函数约束的方式，尽可能的降低数据分布外动作的估计值，鼓励策略选择数据分布内的动作，达到缓解了外推误差的影响[2]。上述算法本质思想都是尽可能少的去评估OOD 动作，这样的做法好处是提高算法稳定性，但缺点也显而易见，就是过于保守，局限性很大，太依赖于数据集的好坏，通过训练可能仅仅学习到次优策略。

为此，不同于以上介绍的方法，本文重新改变对OOD 动作的看法，鼓励算法对OOD 动作进行一定的探索，在数据集较差的情况下也可以取得不错的结果。因此，本文提出了基于双重限制Q 学习的离线强化学习算法DIQL。

1 研究现状

本小节主要介绍目前比较流行的离线强化学习算法。BCQ[3]算法通过限制学习策略接近行为策略分布来抑制外推误差；TD3+BC[4]算法在TD3 算法的基础上，添加了约束学习策略与行为策略距离的正则项；BRAC[5]提出了值函数惩罚vp（value penalty）方法；AWR[6]算法将限制学习策略尽可能的接近行为策略作为约束项，把优势函数作为权重进行策略提升；AWAC[7]算法引入优势函数先进行离线预训练；CQL[8]算法通过学习一个保守的函数来抑制外推误差；IQL[9]算法引入值函数正则项，仅使用数据集内的数据训练策略。

以上提到的大部分算法都有一个共同的局限，就是太依赖于数据集的好坏，泛化能力较差，为了应对外推误差和过于保守的问题，本文提出了DIQL 算法。主要创新点包括：

（1）提出了一种数据增强的方法。对数据集内的状态进行数据增强，并使用贝尔曼误差方程单独训练V 值网络，提高算法的泛化能力。

（2）提出了一种双重限制Q 学习的方法。将经过数据增强的v 值网络作为目标网络来训练Q 值网络，限制算法对OOD 动作的估值在合理范围内，并在策略网络的更新过程中限制策略产生的动作不应远离数据集分布。

（3）对双重限制Q 学习方法进行了理论分析，证明了Q 值函数的可收敛性，并在双足六自由度机器人步态控制环境halfcheetah[10]的不同数据集下对算法的有效性进行了验证。

2 算法介绍

在这一小节，主要介绍DIQL 算法的框架，并从v 值网络、Q 值网络和策略网络[11]3 个部分逐步分析DIQL 算法是如何缓解外推误差和提高探索度的。

2.1 V 值网络

由于v 值网络不需要对动作进行价值估计，将v 值网络作为Q 值网络的目标网络可以有效限制对OOD 动作价值高估的现象。为了设计一个可收敛的v 值网络，本文的主要思路是通过多层感知机[12]来搭建v 值网络，并以贝尔曼误差方程更新v 值网络的超参数ψ。考虑到离线强化学习的数据集是固定的，在算法训练时很容易出现过拟合现象，对状态s进行数据增强，可以提高算法的稳定性和泛化能力，数据增强示意图如图1 所示。

v 值网络的贝尔曼误差方程如公式（1）所示：

式中：s 表示此时此刻的状态；a 表示执行的联合动作；s′表示在状态s 下执行动作a 转移到的下一状态；r 表示在状态s 下执行动作a 得到的立即回报；γ为折扣因子；ψ 为v 值网络的参数；εi∈N（0，σI），σ为一实参。

2.2 Q 值网络

为了得到一个既可准确评估数据集内动作Q值，又可以缓解OOD 动作Q 值高估的Q 值网络，本文将Q 值更新函数划分为2 部分。第1 部分主要通过数据集内的动作，使用贝尔曼误差方程训练Q 值网络；第2 部分将经数据增强后的v 值网络视为目标网络，使用策略πφ采样得到的OOD 动作来训练Q 值网络，Q 值函数更新方式如公式（3）所示：

由公式（3）可以看出，Q 值更新函数的第1 部分目的是提升Q 值网络对数据集内动作价值估计的准确度，第2 部分目的是缓解OOD 动作Q 值高估的问题。与以往的离线强化学习算法思路不同，DIQL算法的工作重心不再是如何避免评估OOD 动作，而是鼓励算法对OOD 动作进行评估。同时，为了缓解外推误差的现象，在公式（3）的第2 部分使用经过数据增强的v 值网络作为目标网络来训练Q 值网络，这样的做法并不代表把所有OOD 动作的Q 估计值都限制到一个很小的范围，策略仍有很大机会去选择OOD 动作，这意味着算法在面对数据集质量较差的情况下更有机会取得令人满意的效果。

2.3 策略网络

根据2.2 小节，得到了一个即可以准确估计数据集内动作的价值，又可以合理估计OOD 动作的Q值网络，但是为了保证Q 值网络对OOD 动作的估值更具可靠性，应当限制策略产生的动作不应离数据集分布较远，这就是本文提到的第二重限制，策略网络的更新方式如公式（4）所示：

式中：L 为MSE 函数；Qmin（s，a′）代表双Q 值网络中Q 值估计较小的价值函数；ζ 为一超参数，通过ζ将策略产生的动作控制在数据集外的一定范围内。DIQL 算法伪代码如表1 所示，DIQL 算法框架图如图2 所示。

表1 DIQL 算法Tab.1 DIQL algorithm

图2 DIQL 算法框架图Fig.2 Framework diagram of the DIQL algorithm

2.4 算法分析

为了探讨使用公式（3）更新Q 值函数的合理性和可靠性，特对Q 值函数的收敛性进行了理论分析及证明。

3 实验

本文使用的实验环境是halfcheetah，如图3 所示。halfcheetah 环境的主要任务是通过施加连续的关节扭矩来驱动双足六自由度机器人的运动。halfcheetah 的回报函数通常根据机器人的前进速度来计算，即当机器人以较高的速度移动时会获得更高的奖励。

图3 Halfcheetah 环境示意图Fig.3 Schematic diagram of the halfcheetah environment

由于离线强化学习算法的训练不需要与环境进行交互，并且数据集由D4RL 提供，不再对halfcheetah环境的基础情况进行过多的介绍，关注的是在相同环境的不同数据集下算法是否均有优异的表现。halfcheetah 的数据类型包括：medium、medium-replay和medium-expert。medium 代表数据集由次优策略生成，medium-replay 代表使用在线强化学习将策略训练至“中等”性能水平时采样得到的数据集，medium-expert 代表数据集由等量的最优策略和次优策略混合生成。本文实验主要包括2 个部分，第1 个部分主要是在halfcheetah-medium 环境中对算法的超参数进行对比实验。第2 部分主要将所提算法与近期流行的离线强化学习算法在halfcheetah 实验环境中进行比较。

3.1 超参数对比实验

对于超参数ξ 的选取，在面对数据集质量不高的情况下，不同的ξ 对算法性能有较大影响，ξ 选取过大会导致算法的约束力降低，Q 值网络虽然对数据集内的动作可以准确估值，但面对OOD 动作仍会面临外推误差的问题，选取过小会导致Q 值网络对数据集内动作估值的精确度降低。将选取［0.1，0.3，0.4，0.9］作为ξ 的取值进行对比试验，实验结果如图4 所示。可以看出，当ξ=0.4 的时候，算法效果最佳。

图4 ξ 值对比实验结果Fig.4 ξ-value comparison experimental results

对于超参数ζ 的选取，当ζ 选取过大会导致OOD动作偏离数据集，导致算法稳定性变差，选取过小则导致算法的探索度降低。本文将选取［0.05，0.2，0.4］作为ζ 的取值进行对比试验，实验结果如图5 所示。可以看出，当ζ=0.2 的时候，算法效果最佳。

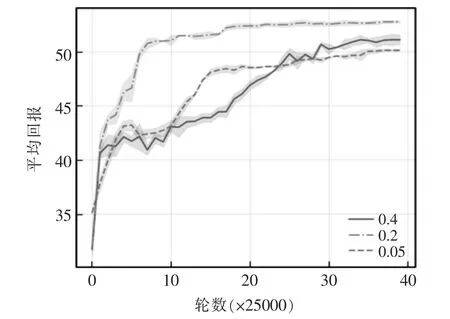
图5 ζ 值对比实验结果Fig.5 ζ-value comparison experimental results

3.2 DIQL 算法性能对比试验

为了验证DIQL 算法提出的有效性，在halfcheetah 环境下3 种不同的离线数据集中进行测试，使用当今较为流行的离线强化学习算法作为对比算法，包括：BC、DT[14]、AWAC、Onestep RL[15]、TD3+BC、CQL 和IQL 算法，为了保证公平性和防止偶然性，学习率均设为0.005，在所有实验环境中均进行了50 次实验，实验数据来自这50 次实验的均值。在不同数据集中的平均归一化分数对比结果如表2 所示，算法中超参数的具体设定值如表3 所示。

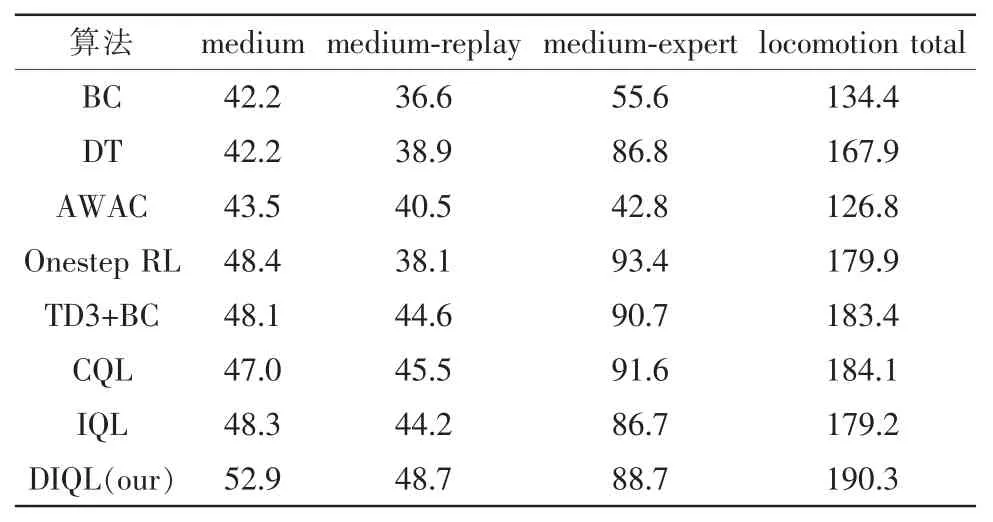
表2 平均归一化分数对比Tab.2 Comparison of average normalized scores

表3 实验数据Tab.3 Experimental data

由表3 可以发现，由于目前流行的离线强化学习算法对OOD 动作的限制，导致算法的大部分的训练数据均来自数据集中的元组，当halfcheetah 数据集的质量较差时，如medium 或者medium-replay，算法无法学习到最优策略，DIQL 算法打破这种固有思维，在双重限制Q 学习的基础上允许算法对OOD动作进行一定的探索，往往可以探索到相比于仅在数据集内更好的策略。

4 结语

为了缓解离线强化学习算法的学习效果太依赖于数据集的质量的问题，本文提出了基于双重限制Q 学习的离线强化学习算法DIQL，引入了双重限制Q 学习方法，限制算法对OOD 动作的估值在合理范围内，鼓励算法进行一定的探索，并且使用数据增强的方法提高了算法的泛化能力。最后在双足六自由度机器人halfcheetah 环境的数据集上对算法的有效性进行了验证，实验结果表明，在面对数据集质量较差的情况下，算法的学习效果有所提升。但是，在面对数据集质量较好的情况下，算法如何自动调节探索度以提高性能，将在后续工作中进行更加深入的研究。