构网型变流器多环控制阻抗建模与稳定性分析

郑雨萱，陈兰杭，李先允，程煜

（1.南京工程学院 电力工程学院，南京 211167；2.国网江苏省电力有限公司镇江分公司，镇江 212000）

并网变流器作为大量新能源并网的关键组成器件被广泛使用。传统并网变流器使得电力系统呈现低惯量、欠阻尼的系统特性，降低了电网电压频率支撑力[1]。为此，近年来国内外学者提出了构网型变流器以及多种控制技术。其中虚拟同步发电机（VSG）控制[2]模拟同步发电机运行机理，不借助锁相环实现同步，为系统提供虚拟惯性和阻尼，有利于改善系统稳定性。

对变流器多环控制并网稳定性研究，可以使用阻抗分析法。文献[3]采用谐波线性化方法建立VSG序阻抗模型，但忽略了VSG 输出端电压波动，未考虑无功电压控制环的影响；文献[4]考虑滤波电路、无功环路和控制延时的影响，建立了较完整的VSG序阻抗模型。但上述研究仅针对只含有功率控制环的单环控制构网型变流器，均忽略了电压电流控制双环的影响。

本文在现有研究基础上，针对虚拟同步控制的构网型变流器，采用谐波线性化方法建立考虑电压电流解耦控制双环的多环控制变流器序阻抗模型。对比分析两种控制方式下变流器在不同频段阻抗差异，提出引入虚拟阻抗提高多环控制变流器并网稳定性。最后对分析结果进行仿真实验验证。

1 构网型变流器序阻抗模型

1.1 拓扑结构和控制原理

构网型变流器并网拓扑如图1 所示。主电路中，Lf、Rf、Cf为滤波电感及其寄生电阻和滤波电容；Le、Re和Zg为变流器等效连接电感、电阻和电网等效阻抗；PCC 为变流器并网点。控制环路主要由功率控制环，电压电流控制双环组成。

图1 变流器并网拓扑图Fig.1 Topology diagram of grid connected converter

变流器功率控制环控制原理如图2 所示。功率控制环模拟同步发电机机械与电磁特性，其数学模型表示为

图2 功率控制环控制框图Fig.2 Power control loop control block diagram

式中：Pref、Qref与Pe、Qe为有功和无功功率参考值与瞬时值；ω 和ωn是变流器瞬时角频率与额定角频率；J 为虚拟转动惯量；K 为无功惯性系数；Dp和Dq为有功和无功阻尼系数；Vm和Vn为变流器采样电压幅值与输出电压额定值；Em和θ 为功率控制环输出参考电压幅值和相位。

为了更加精确地控制，引入考虑解耦的电压电流控制双环，其传递函数表达式为

式中：vdref、vqref与idref、iqref为电压环和电流环参考值；erd和erq为控制双环输出信号；vd、vq、iLd、iLq与id、iq是电容电压v、滤波器电感电流iL和输出电流i 在dq轴上分量；Gv（s）=kvp+kvi/s 为电压环PI 调节器；Gi（s）=kip+kii/s 为电流环PI 调节器。

本文将只含有功率控制环的变流器称为单环控制变流器，将含有功率控制环和内部电压电流控制双环的变流器称为多环控制变流器。

1.2 构网型变流器序阻抗建模

利用谐波线性化构建多环控制变流器正负序阻抗模型。以正序为例，在PCC 处注入fp频次正序电压扰动，根据2 倍镜像频率耦合效应，主电路可分解为fp频次和fp-2 f1频次等效电路，其小信号模型为

式中：滤波电容电压va[f]、输出电流ia[f]、电感电流iLa[f]具体定义分别为

正序电压扰动经过功率控制环引起相角扰动Δθ，使得θ＝θ1+Δθ，其中θ1＝ω1t 为基波电压相位角。va[f]、ia[f]和iLa[f]经过park 变换得到dq 轴下的电压电流表达式为

式中：Vd=V1，Vd=0，Δvd0=Vp+Vp2，Δvq0=∓jVp±jVp2，Id=I1cos φi1，Iq=I1sin φi1，Δid0=Ip+Ip2，Δiq0=∓jIp±jIp2，ILd=IL1cos φi1，ILq=IL1sin φi1，ΔiLd0=ILp+ILp2，ΔiLq0=∓jILp±jILp2。

忽略高频分量，利用频域卷积定理得到变流器有功功率和无功功率频域表达式：

根据式（1）和式（2）功率控制环数学模型，忽略二次项小信号量，得到θ 和Em频域表达式：

电压电流控制双环电压环参考值由功率控制环产生，其中vdref[f]=Em[f]，vqref[f]=0，结合式（3）和式（4），并经过Park 坐标反变换求得a 相桥臂电压响应ea[f]，如式（20）所示：

式中：Mp（s∓jω1）、Np（s∓jω1）、Lp（s∓jω1）、Mp2（s±jω1）、Np2（s±jω1）、Lp2（s±jω1）为电压电流相关分量的系数。

为了消去fp-2 f1频次耦合电流，将式（20）代入式（6）中，得到Ip2关于滤波电容电压和输出电流表达式：

式中：Dp2（s）=［（s∓jω1）Le+Re］-Lp2（s）+｛［（s∓jω1）Lf+Rf］-（-Gpi（s）-jωnLf）｝×｛［（s∓jω1）Le+Re］（s∓jω1）Cf+1｝。

将式（21）带入式（20），并结合式（5），求解得到变流器正序阻抗如式（22）所示。负序阻抗与正序阻抗求解过程相似，其结果如式（23）所示：

2 阻抗特性与并网稳定性

2.1 单环、多环控制变流器阻抗特性差异

构网型变流器主要参数如表1 所示。依据表1参数数据绘制变流器单环控制[4]、多环控制下正负序输出阻抗曲线对比图，如图3 所示。

表1 构网型变流器主要参数Tab.1 Main parameters of grid-forming converter

图3 变流器与电网阻抗特性曲线Fig.3 Sequence impedance curves of converter and grid

引入电压电流双环控制前后比较分析如下：

（1）200 Hz 以上的中高频段，变流器单环控制正负序阻抗特性主要受主电路滤波器以及等效连接阻抗影响，在650 Hz 左右呈现幅值较大，相角180°突变的谐振峰，系统可能在该频率处出现谐波振荡。改为多环控制后，变流器谐振频率后移，谐振幅值大大降低，避免其与电网阻抗幅频曲线交截，改善了变流器稳定性。

（2）200 Hz 以下的低频段，变流器单环控制正负序阻抗特性主要呈现功率控制环特性，受功率环控制参数影响，正负序阻抗接近感性，变流器正负序阻抗相位裕量较大，满足系统稳定要求。改为多环控制后，由于电压电流q 轴分量在正负序上相位相反，正负序相位变化呈现相反变化趋势，正序阻抗相位大幅度降低呈现容性，将系统引入较小的相位裕度状态，降低变流器稳定性能，相反负序阻抗相位提高，使系统具有较好的相位裕度。

2.2 并网稳定性分析

变流器并网时，由阻抗稳定性准则可知，当电网阻抗与变流器输出阻抗的幅频曲线相交频率点处的相角裕度γ=180°-为正，系统稳定。在工程应用中，为增加变流器并网交互系统的鲁棒性，通常要求γ＞30°[5]。

如图3 所示，电网阻抗从下至上不断增大，分别取1.5 mH、4 mH、11 mH。不同电网阻抗与单环控制正负序阻抗在不同频率交截，交互系统相位裕度均大于0，满足系统稳定要求。但是在高频区域859.6 Hz处，变流器并网系统的相位裕度γ=0.92°较小，易引起整个系统的振荡。采用多环控制后，无论电网阻抗如何变化，系统相位裕度大于0，但均小于30°。如当Zg=4 mH 时，3.128 Hz 幅频曲线交截处相位裕度γ=20.3°，系统稳定性能差。

3 基于虚拟阻抗的变流器并网改善策略

通过前述分析比较，多环控制变流器低频正序输出阻抗容性特征主要是由电压电流控制双环引起的。若是在多环控制基础上，保持高频阻抗特性不变，改善变流器正序阻抗低频相位裕度，将提高变流器并网稳定性。

在变流器电压控制环中引入虚拟阻抗，其中，Rv为虚拟电阻，Lv为虚拟电感。引入虚拟阻抗后，电压参考值表达式改写为式（24），构建含虚拟阻抗的变流器阻抗模型：

如图4 所示，电网阻抗从下至上分别取1.5 mH、4 mH、11 mH。在多环控制基础上，令虚拟电阻Rv=0.2，虚拟电抗Lv=1 mH，绘制相关阻抗曲线。可以看出加入虚拟阻抗后，变流器正序阻抗低频幅值和相角均有明显提升，高频阻抗特性基本保持不变；而变流器负序阻抗低频幅值提高但相位降低。不同电网阻抗下，系统均有充足的相位裕度，如当电网阻抗Zg=4 mH 时，变流器正序阻抗与电网阻抗在低频区域13.19 Hz、46.19 Hz 和55.43 Hz 交截，负序阻抗在低频区域12.06 Hz 与电网阻抗交截，交互系统相位裕度均大于30°，满足系统稳定要求。因此，加入虚拟阻抗提高了变流器基频及以下区间相位裕度，有利于系统稳定。

图4 加入虚拟阻抗的变流器输出阻抗模型Fig.4 Output impedance model of inverter with virtual impedance

4 仿真与实验验证

为了验证上述理论分析的正确性，本文在MATLAB/Simulink 中按照表1 所示的系统参数搭建了仿真模型，并进行实验验证。

如图5、图6 和图7 所示，给出了电网阻抗Zg=4 mH 时单环控制、多环控制、虚拟阻抗控制下，构网型变流器0 s 并网电压电流波形，变流器稳定运行时电压电流波形图。

图5 单环控制下变流器并网电压电流分析Fig.5 Analysis of grid connected voltage and current of converter under single-loop control

图6 多环控制下变流器并网电压电流分析Fig.6 Analysis of grid connected voltage and current of converter under multi-loop control

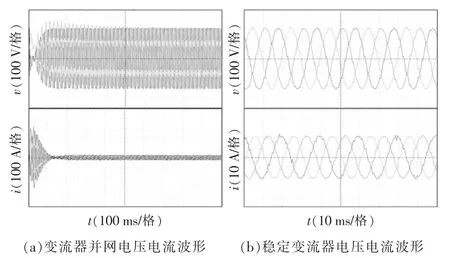
图7 虚拟阻抗控制下变流器并网电压电流分析Fig.7 Analysis of grid connected voltage and current of inverter under virtual impedance control

对比图5 和图6 可以看出，单环控制下的电流波形稳定后存在明显谐波振荡；相比而言，采用多环控制后，并网时刻变流器具有约单环电流2 倍的电流脉冲，经过较长恢复时间，电流才趋于稳定，稳定后的电压电流不存在谐波振荡，均与图3 中的理论分析相吻合。

对比图6 和图7 可以看出，虚拟阻抗改善控制下的电压电流稳定性，并网电流脉冲较小，能更快趋于稳定且稳定后电流谐波含量极小，验证了图4理论分析的准确性。

5 结语

本文考虑构网型变流器多环控制稳定性问题，分析了电压电流控制双环对变流器不同频段稳定性影响，并在此基础上提出了基于虚拟阻抗的改善控制策略，通过理论分析和仿真实验验证，主要结论如下：电压电流控制双环使得变流器正序输出阻抗在低频呈现容性，降低了低频稳定性。通过降低变流器高频幅值，避免变流器与电网交互，提升了构网型变流器高频稳定性；在电压电流控制双环中引入虚拟阻抗改变了变流器的低频段阻抗特性，提高了相位裕度，增加了交互系统稳定性。但是由于q轴分量在正负序上的相反性，正序相位裕度提高的同时，负序相位裕度减小，虚拟阻抗的选取应兼顾正负序阻抗特性变化。