基于QPSO-LSTM 的短期电力负荷预测

祝少卿，张钧皓，于禄霏，张沥新，叶靖南

（辽宁工程技术大学电气与控制工程学院 辽宁 葫芦岛 125000）

0 引言

随着“双碳”目标的制定，近年来，电力负荷预测在能源管理和电力系统运行与调度中扮演着至关重要的角色。为了提高电力负荷预测的准确性和精度，许多研究人员开始将深度学习模型应用于该领域。

范茜茜等［1］提出了一种基于N-BEATS 与辅助编码器的短期电力负荷预测模型，其模型可充分挖掘负荷序列中的趋势特征与周期性特征，提升短期电力负荷预测精度。刘林虎［2］则利用神经网络在处理时间序列数据中的优势，初步建立门控循环单元（gate recurrent unit，GRU）－卷积神经网络（convolutional neural network，CNN）深度神经网络，又通过实验讨论了注意力机制在网络中不同位置的影响，建立了GRU-CNN-Attention 深度神经网络模型。

综上所述，基于神经网络的短期电力负荷预测已成主流，本文提出了一种基于量子粒子群优化（quantum particle swarm optimization，QPSO）算法和长短期记忆网络（long short-term memory，LSTM）的短期电力负荷预测模型，采用比利时地区电力负荷数据进行算例分析以验证基于QPSO-LSTM 的短期电力负荷预测模型的有效性。

1 概述

基于QPSO-LSTM 模型的电力负荷预测方法是一种结合了量子粒子群优化算法和长短期记忆网络的预测方法。QPSO 算法被用来优化LSTM 神经网络中的参数。 通过结合QPSO 算法和LSTM 神经网络，基于QPSO-LSTM 模型的电力负荷预测方法能够充分利用历史负荷数据中的信息，提高预测的精度和稳定性。 该方法在实际应用中具有一定的优势，并且可以进一步改进和扩展，以应对电力负荷预测中的挑战和需求。

2 算法实现

2.1 LSTM

LSTM 是一种用于处理序列数据的特殊循环神经网络。 不同于循环神经网络（recurrent neural network， RNN）只考虑最近的状态，LSTM 在时间序列数据的处理上表现出优异的性能。 在实际应用中，LSTM 通常通过堆叠多个LSTM 单元来构建深层网络。 这样可以增强模型的表达能力，并提高其在复杂任务上的性能。

LSTM 单元的内部结构对应的数学表达式如式（1）～式（5）所示［3］。

式（1）～式（5）中，ft表示遗忘门的输出；σ为sigmoid 激活函数，将ht－1和xt输入σ函数中，输出介于0～1 之间，0 表示完全丢弃该内容，1 表示保留；it为输入门的输出，控制候选记忆单元gt的删减或保留；ot为输出门；W为对应的权重参数；b为对应的偏置。

2.2 QPSO

QPSO 算法通过引入量子力学的思想，对粒子群优化（particle swarm optimization，PSO）算法进行了改进。 QPSO算法的粒子采用薛定谔方程进行描述，然后利用蒙特卡洛模拟得到粒子位置，分析如式（6）所示。

式（6）中，u为随机数，u∈［0，1］，其值服从正态分布；pi，d（t）为第i个粒子在第t次迭代时的最优位置；L为量子系数；pi，d（t）、L的值可根据式（7）～式（10）确定。

式（7）～式（10）中：M为粒子个数；d为维数；φ为随机数；φ∈［0，1］，其值服从正态分布；pg，d（t）为所有粒子在第t次迭代时的最优位置，g表示最优个体；z为所有粒子在第t次迭代时最优位置的平均值；β为收扩系数；m、n为收扩系数参数。 综合式（6）～式（10），得到QPSO 算法粒子位置的更新方程如式（11）所示：

2.3 使用QPSO 优化LSTM 模型参数的方法

使用QPSO 优化LSTM 模型的步骤如图1 所示。

图1 使用QPSO 优化LSTM 模型流程图

步骤1：首先根据LSTM 模型的参数个数和取值范围，初始化一定数量的粒子，并在参数空间中随机分布。

步骤2：根据当前粒子的参数向量，构建LSTM 模型，并利用训练数据进行训练。 然后，使用验证集或交叉验证来评估模型的性能，计算该粒子的适应度值。 适应度函数可以选择模型在验证集上的准确性或其他性能指标。

步骤3：再根据QPSO 算法的更新公式，更新每个粒子的速度和位置。 更新公式使用了粒子自身历史最好解和全局最好解，以及一些随机因素来调整搜索过程。

步骤4：迭代执行步骤2 和3，直到达到预定的迭代次数或满足停止准则（如适应度收敛）为止。 在迭代结束后，选择具有最佳适应度值的粒子作为最优解。 该粒子所对应的参数向量即为优化后的LSTM 模型的参数。

步骤5：将最优参数应用于LSTM 模型，并在独立的测试集上进行评估。

3 实验分析

3.1 数据采集与处理

本文采用比利时某地区某年6 月份电力负荷的数据，以15 天负荷数据作为预测样本，该数据以15 min 为间隔进行采样。 之后对数据进行预处理和归一化，归一化操作如式（12）所示。

将处理完的数据分成两部分，前70%的样本作为训练集得到模型参数；后30%作为测试集，用来验证模型预测精度。 训练集和测试集数据情况如图2 所示。 横坐标为采样时间编号，纵坐标为归一化操作后的负荷数据。

图2 训练集和测试集数据情况

3.2 评价标准

本文选取的各种模型预测精度评价指标为均方根误差（root mean square error，RMSE）、平均绝对误差（mean absolute error，MAE）、平均绝对百分比误差（mean absolute percentage error， MAPE）和决定系数R2（R-square）。 作为评价基准［4］，其表达式分别如式（13）～式（16）所示。

RMSE 是衡量预测结果与实际观测值之间差异的指标；MAE 是对预测误差绝对值的平均值进行衡量的指标；MAPE 是预测误差相对于实际值的百分比平均值。 以上3个数越小表示模型的拟合效果越好、预测准确性越高、相对误差越小。R2是评估模型拟合程度的指标，其数值越接近1 表示模型对数据的拟合效果越好。

3.3 实验结果分析

利用训练集数据构建QPSO-LSTM 模型、传统PSO 优化的LSTM 模型和传统LSTM 模型，分别进行负荷预测。其预测结果如图3 所示。

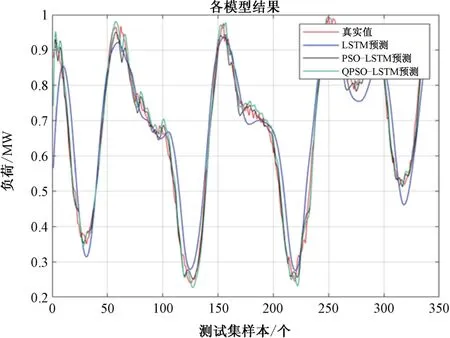
图3 各模型预测结果

如表1 所示，根据以上各项结果，可以看出PSO-LSTM和QPSO-LSTM 相较于传统LSTM 算法在预测效果上有明显的提升，已经能够更准确地预测目标变量的数值，并能够更好地拟合观测数据。 并且QPSO-LSTM 算法的预测效果比PSO-LSTM 算法更好。

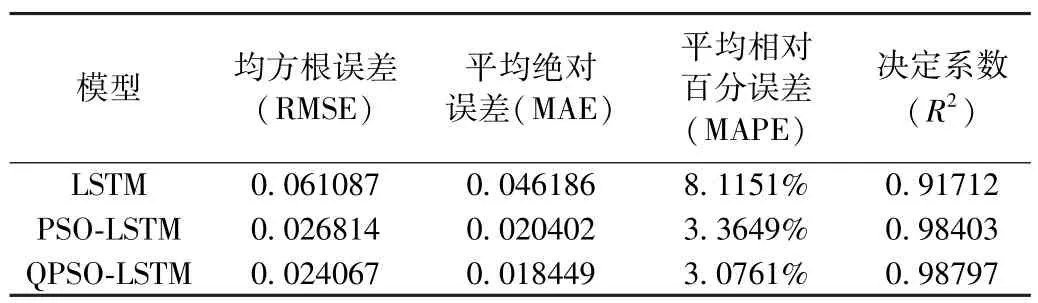
表1 各模型结果误差分析

4 结语

综上所述，本文应用QPSO-LSTM 模型进行负荷预测，相比于传统模型，QPSO-LSTM 网络模型针对时间序列数据具有较高的预测精度，可以更准确地预测时间序列数据的未来趋势和变化。 QPSO-LSTM 算法在短期电力负荷预测方面具备较高的研究应用价值。