基于贝叶斯神经网络的船用惯导定位修正方法

周红进, 宋 辉, 范文良, 王 苏, 谷东亮

(1. 海军大连舰艇学院航海系, 辽宁 大连 116018; 2. 国家检察官学院信息技术部, 北京 102206)

0 引 言

惯性导航系统(inertial navigation system, INS)能够独立工作、可在不依赖于任何外部信息的条件下,为载体提供位置、速度、航向和姿态等全量导航信息。INS的这种优越特性使其在军事领域中得到了广泛应用。船用INS具有工作时间长、对定位精度要求高的特点,独立自主工作的INS的定位误差随着时间的延长逐渐发散且超出误差限制。为此,通常将INS与全球卫星导航系统(global navigation satellite system, GNSS)进行组合导航以提高INS的定位精度、延长INS保精度的时间。在GNSS失效时,INS的定位误差将快速发散。

为了提高惯导独立工作时的定位精度,传统的做法是测量陀螺漂移和加速度计零偏并在惯导定位解算过程中加以补偿,如陀螺壳体旋转法、平台旋转调制法、H调制法、应用监控陀螺(监控器)法等[1-4],这些方法都是陀螺漂移的自校正方法,需要对INS进行补充硬件设计开发,提高了INS的控制复杂度,也增加了INS的成本。也有利用外部提供的准确位置(GNSS定位信息)和航向信息估计陀螺漂移,从而对INS进行校正的[5-9]方法。在深远海航行环境下,一旦遭遇GNSS拒止,这种方法难以实现。还有通过零速校正提高INS定位精度的[10]方法,这种方法需要舰船周期性的停车,直至获得零速才可实施,这对于承担作战任务的舰艇而言是不切实际的。

近年来,基于神经网络的深度学习技术发展迅速,在人工智能等自主学习领域已经展现出巨大的应用前景。神经网络在惯性导航领域的应用研究也开始增多[11-23]。文献[11]和文献[12]率先使用单隐藏层的反向传播神经网络(back propagation neural net, BPNN)来预测定位和速度误差。文献[13-16]将小波神经网络和强跟随器相结合,利用位置信息提出INS误差补偿方法。文献[17-19]总结了很多基于人工智能的定位误差抑制算法,提出了自适应模糊神经网络。这些早期的文献从理论角度探索了神经网络在惯性导航领域中的应用。文献[20]提出将长短时记忆(long short term memory, LSTM)网络用于训练微机电系统(micro-electric mechanical system, MEMS)的误差修正模型,在GNSS失效时将MEMS输入至训练得到的模型,得到东向、北向位置增量,从而提高MEMS独立工作时的定位精度。文献[21]以当前时间、东北向速度增量、姿态增量为输入,以东北向位置增量和航姿增量为输出,构建了基于Bagging的神经网络,在全球定位系统(global position systern, GPS)失效时,利用训练得到的神经网络预测东北向位置增量和航姿增量,进行定位修正。文献[22]采用BPNN神经网络直接拟合加速度计脉冲输出与速度增量间的计算关系,在高超声速飞行器飞行初始阶段存储INS数据和卫导数据,从中段开始训练网络,在卫导中断的末段启用神经网络计算速度增量,开始定位解算。文献[23]提出改进膨胀卷积神经网络对惯性测量单元(inertial measurement unit, IMU)的陀螺仪误差进行标定补偿,利用时间卷积神经网络检测车辆运动状态(零速、平面零速、垂向零速),结合二者处理结果,采用不变扩展卡尔曼滤波(invariant extend Kalman filter, IEKF)进行信息融合,估计车辆位置。上述方法训练网络的输出有陀螺漂移、速度增量、位置增量,都需要考虑INS的误差模型,均存在训练样本少、训练时间长,模型参数相对固定、训练得到的模型在后续INS独立工作时保精度时间不明等问题。

本文提出一种改进的BPNN,该神经网络由输入层、1个隐藏层和输出层组成,以INS原始数据作为输入,以载体位置作为输出,直接训练网络建立INS解算位置的数学模型。采用Bayesian算法动态训练调整各层间的权重系数和偏差值,以抑制由陀螺仪漂移和加速度计零偏造成的定位误差,结合理论分析和试验研究确定了神经元个数、训练数据集的分配方案。实船测试结果表明,INS独立工作时,经过神经网络修正后的定位误差显著低于INS自身的定位误差,且延长了INS保精度的时间。

1 船用捷联惯导解算模型

船用捷联INS(strap-down INS, SINS)在计算机中建立数学平台,计算机根据陀螺仪和加速度计的测量输出解算载体位置、速度、航姿等信息。图1所示为船用SINS解算导航参数的流程[24]。

图1 船用SINS解算导航参数流程图Fig.1 Navigation parameters resolution flowchart of ship SINS

1.1 导航参数解算

对于船用SINS,姿态解算非常关键。通常选择当地地理水平坐标系作为导航坐标系。载体的姿态是指载体坐标系相对导航坐标系的旋转关系。可以采用方向余弦矩阵算法解算载体姿态。

(1)

(2)

方程式(1)的解可以写成如下形式:

(3)

由Ck+1即可解算载体姿态。

船用捷联惯导速度解算方程为

(4)

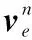
载体的位置更新方程为

(5)

式中:P为载体在导航坐标系下的位置矢量,ξ为载体线速度到经纬度变化率的转换矩阵。

式中:RM为卯酉圈半径;RN为子午圈半径;h为距离地球表面的高度;φ为载体纬度。

1.2 误差方程

SINS陀螺仪和加速度计的输出包含常值误差和随机误差。由式(1)、式(4)、式(5)可以得到SINS误差方程

(6)

2 定位修正模型

2.1 BPNN模型

船用SINS原始输出为陀螺仪测量的载体角速度、加速度计测量的载体线加速度。在已知初始位置和速度的情况下,即可根据式(1)、式(4)、式(5)进行位置、速度和姿态解算。INS定位结果与陀螺仪和加速度计的测量量以及时间存在多输入与多输出的映射关系。

(λ,φ)=f(Δt,λINS,φINS,vx,vy,Ax,Ay,Az,ωx,ωy,ωz)

(7)

考虑使用一个合适的神经网络拟合其映射关系f,将INS误差补偿模型包含进神经网络拟合的映射关系中,网络直接输出修正后的经纬度。这种方法既可以降低根据式(6)建立的误差修正模型带来的神经网络复杂度,提高网络训练速度,也有助于提高INS定位修正的效率。

BPNN具有强大的非线性映射能力,且具备结构简单的优点[25],非常适合拟合陀螺仪和加速度计的测量值与INS解算经纬度之间的非线性函数关系。考虑到INS误差有其自身内在的规律,为了避免过拟合,提高神经网络的泛化性,将INS解算的经纬度作为第二输入,这样就可构建一个输入为x1=(Δt,λINS,φINS,vx,vy,Ax,Ay,Az,ωx,ωy,ωz)、x2=(λGNSS,φGNSS),输出为y=(λGNSS,φGNSS)的13输入2输出的BPNN结构。根据模型复杂度的需求,建立含有一个隐藏层的网络进行训练。如图2所示为BPNN训练模型。当GNSS有效时,x2=(λGNSS,φGNSS),当GNSS失效时,x2=(λINS,φINS)。

图2 BPNN训练模型Fig.2 BPNN training model

隐藏层激活函数为tansig,输出层激活函数为purelin,表达式为

(8)

GNSS有效时,INS可以正常获取GNSS定位信息。因此采用GNSS定位结果与INS定位结果的差值的均方误差(mean square error, MSE)作为损失函数,以评价网络训练效果。MSE的计算公式为

(9)

式中:K为训练样本中的数据量;λGNSS,φGNSS为卫星导航经纬度;λy,φy为神经网络输出经纬度。

2.2 基于Bayesian权重更新算法

神经网络的权重直接决定了模型的性能。权重更新算法直接影响模型对输入输出关系的拟合能力。常用的L-M(Levenberg-Marquart)算法是牛顿法的改进,能够避免在雅克比矩阵奇异或病态时发生的不收敛的情况。该算法通过直接计算黑塞矩阵,减少了训练中的计算量,对于中等规模的BPNN有较快的收敛速度[26]。但L-M算法基于点集合训练权重参数,是一种根据反向传播误差确定性更新权重参数的方法,容易过拟合模型。因此,这种方法对于包含各种随机噪声的输入数据集抑制效果较差,模型泛化能力不足。

考虑到INS误差周期长,训练数据集必须足够长,即至少需要24 h的历史数据才能训练出符合INS误差规律的解算模型。本文采用Bayesian算法进行权重更新。Bayesian权重更新算法不是训练单个网络,而是训练网络集合,每个网络的权重来自共享的学习概率分布。Bayesian估计与最大似然估计的区别是Bayesian估计可求出权重参数W的后验分布P(W|D)(D为输入数据集),这样就可以为神经网络的预测引入不确定性,从而提高神经网络的泛化能力。

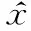
(10)

式中:ΕP(W|D)为期望值。

式(10)需要计算在P(W|D)上的所有可能的神经网络的预测值,但是后验分布P(W|D)难以直接计算。为了计算P(W|D),可以采用变分的方法,使用一个由一组参数θ控制的分布q(W|θ)逼近真正的后验分布P(W|D)。比如,可以用高斯分布(μ,σ)近似θ,这样就把求后验分布的问题转化为了求最优θ的问题。这个过程可以通过最小化两个分布的KL(Kullback-Leibler)散度实现:

(11)

式(11)可以写成目标函数:

F(D,θ)=DKL[q(W|θ)|P(W)]-Εq(W|θ)[lgP(D|W)]

(12)

式(12)的第一项就是变分后验和先验的KL散度,第二项的取值依赖于训练数据。第一项叫做复杂性代价,第二项叫做似然代价,用于描述对样本的拟合程度。

对于P(W),可以给出一个混合尺度高斯先验分布:

(13)

即对于每个权重,其分布的先验都是两种相同均值、不同标准差的高斯分布的叠加。

继续对目标函数式(11)取近似:

(14)

式中:W(i)是处理第i个数据点时的权重采样。

根据式(14)可以计算式(12),由式(12)可以计算θ的最优分布,进而逼近后验分布P(W|D)。

2.3 模型训练

对于定位修正模型,输出为经度、纬度。输入为不同时刻的INS原始数据和卫导定位结果,包括:时间、东向、北向、天向加速度计测量输出和陀螺仪测量输出,INS东向、北向速度,INS经度、纬度,卫导经度、纬度。

输入序列:x1=(t,λINS,φINS,vx,vy,Ax,Ay,Az,ωx,ωy,ωz)i,x2=(λGNSS,φGNSS)i。输出序列:y=(λ,φ)i。

训练流程如图3所示。当GNSS有效时,利用GNSS定位结果,通过反向传播的随机梯度下降法来计算神经网络参数。当GNSS失效时,采用SINS的数据取代GNSS,神经网络工作在自主修正模式。

图3 算法训练流程Fig.3 Algorithm training flowchart

由于INS定位误差包含3种分量:舒勒周期误差、地球周期误差和傅科周期误差。舒勒周期误差调制傅科周期误差。为了避免训练出的模型失真,即背离INS解算数学关系,取训练数据集持续时间约为24 h。

满足如下条件之一,则停止训练:

(1) 达到最大迭代周数1 000;

(2) 训练时间达到最大限制;

(3) 训练MSE达到0;

(4) 性能梯度低于最小梯度(一般为1e-7)。

3 试验及结果分析

神经网络训练计算环境为:CPU:i7_6700@3.4GHz,内存16.0 GB,显卡HD530,操作系统为Windows7。

为了验证本文提出的INS定位修正方法,实船采集了某型船用SINS的数据和GNSS定位数据。GNSS系统为Trimble MS860接收机。海上采集数据持续时间为24 h,舰船航行轨迹如图4所示。

图4 舰船航行轨迹Fig.4 Ship trajectory

SINS数据输出频率为1 Hz,GNSS数据输出频率为1 Hz。在训练阶段,SINS与GNSS进行组合导航,以修正INS定位结果。在验证阶段,关闭GNSS数据,直接使用神经网络修正SINS定位结果。

3.1 神经元个数对定位修正的影响

神经元的个数与神经网络处理的问题的复杂度有关,也直接影响训练效率和网络的后续处理能力和泛化能力。根据Kolmogorov定理,神经元个数可计算如下:

Nh=2n+1

(15)

式中:n为输入层结点个数。另外,还有一种确定神经元个数的计算公式:

(16)

式中:Ns为训练集样本数据点数;Ni为输入层结点个数;No为输出层结点个数;α=[2 10]。

本文建立的网络输入层节点个数为13,输出层节点个数为2,训练样本数据点数约为86 400。根据式(15),神经元个数为27。根据式(16),神经元个数最少为576。本文参考式(15)、式(16)的结果,采用试验的方法确定使用的神经元个数。

将神经元个数分别设置为30、40、50、60。图5所示为训练迭代周数和训练时间随神经元个数变化的曲线图。图6所示为GNSS关闭后,神经网络修正后与INS独立工作定位误差比对曲线图。表1为神经网络修正后与INS独立工作定位结果。

表1 INS独立工作与神经网络修正后定位误差Table 1 Position error between independent-working INS and INS with neural networking correction

图5 训练周数和时间与神经元个数关系曲线Fig.5 Training epoch and duration vs. number of neuron

图6 INS独立工作与神经网络修正后定位误差比对曲线Fig.6 Comparison curve of position error between independent-working inertial navigation system and INS with neural networking correction

从图5可以看出,随着神经元个数的增加,训练时间显著延长,但训练周数变化微小。这说明随着神经网络复杂度的增大,训练时间成本会显著增大,对于对实时性要求高的应用,则对硬件资源的要求会显著提高。

从图6可以看出,神经网络修正INS定位的效果并不一定随着神经元个数的增加而变好。神经元个数为30时,在2 h内,神经网络修正后定位误差一致低于INS独立工作时的定位误差。当神经元个数为40时,在约3 100 s内,神经网络修正后的定位误差小于INS独立工作时的误差。在3 100 s之后,神经网络修正后的定位误差发散速度显然要比INS独立工作时快;6 800 s之后,神经网络修正后的定位误差显著超过INS独立工作的定位误差,神经网络已经不具备误差修正能力。当神经元个数为50时,在2 h内,神经网络修正后定位误差一致明显低于INS独立工作的误差,最小误差一度为0 m,且误差随时间发散速度低于INS独立工作时的速度。当神经元个数为60时,在约7 200 s内,神经网络修正后的定位误差小于INS独立工作时的误差,在其之后神经网络修正后的定位误差开始加速随时间发散,且大于INS独立工作时的误差。

从表1可以发现,神经元个数为50时,对INS定位修正的效果最好,其中误差均值为640.9 m、均方根误差为342.4 m,最大值为1 152.8 m;相比INS独立工作的原值,误差均值下降63%,均方根误差基本不变,最大值下降约50%,最小值为0 m。如图7所示为修正前后INS定位轨迹与GPS定位轨迹。

图7 INS独立工作定位轨迹与修正后轨迹(GPS关闭后2 h)Fig.7 Independent-working INS position trajectory and trajectory with correction (with GPS-off of 2 h)

分析出现上述结果的原因是:当神经元个数不足时,网络对INS解算位置的数学关系拟合度不够,导致误差偏大;当神经元个数过多时,网络对INS解算位置的数学关系拟合过度,对由于陀螺漂移和加速度计零偏的随机性引起的误差修正缺乏弹性。合适的神经元个数,既能实现INS位置解算模型的拟合,也保证了神经网络具有一定的泛化能力,从而具有更好的误差修正能力。

确定神经元个数为50,通过试验比较本文采用的基于Bayesian的权重参数更新方法与传统的基于L-M算法更新网络权重参数的方法训练得到的模型性能。表2列出了两种方法的训练时间、占用内存、模型计算时间、修正后的INS定位误差。其中:训练持续时间是指利用约24 h的INS和GNSS数据训练出定位误差修正模型参数所经历的时间;占用内存是指训练模型所需要的内存;模型计算时间是指批量处理GNSS关闭后的2 h内INS独立定位数据所经历的时间;修正后的INS定位误差是指经过神经网络模型修正INS原始定位结果后与GPS定位结果进行比对而得到的误差。从表2可以看出,L-M方法的模型训练迭代周数和训练时间相比Bayesian方法多约30%,占用内存多90%,模型计算时间接近。L-M修正后INS定位误差均值为2 941.2 m,误差均方根为2 190.1 m,最大误差为16 803.2 m,各项误差指标远大于Bayesian方法的修正结果。L-M方法修正后误差曲线如图8所示。由图8可以发现,在前3 000 s,L-M方法对INS定位误差具有一定效果,在约3 000 s后,L-M算法已经不具备修正INS定位误差的能力了,且误差曲线中包含了大量的噪声。比对试验结果进一步验证了L-M算法基于点集合训练权重参数导致的过拟合问题。

表2 两种方法模型性能比较Table 2 Comparison of model performance between two methods

图8 INS独立工作与L-M算法修正的定位曲线(神经元个数为60)Fig.8 Position curve of independent-working INS and INS with L-M algorithm correction (60 neurons)

3.2 数据分配对定位修正的影响

确定神经元个数为50。实验不同数据分配(即训练集、验证集、测试集比例分布)方案对定位修正的影响。

分配方案A:样本数据个数为76 755,从数据样本中产生153 510个训练数据,其中50%的数据(76 754个)用于训练网络,25%的数据(38 378个)用于检测网络的泛化能力,25%的数据(38 378个)用于独立评估网络在训练中和训练后的性能。

分配方案B:样本数据个数为76 755,从数据样本中产生153 510个训练数据,其中70%的数据(107 456个)用于训练网络,15%的数据(23 027个)用于检测网络的泛化能力,15%的数据(23 027个)用于独立评估网络在训练中和训练后的性能。

分配方案C:样本数据个数为76 755,从数据样本中产生153 510个训练数据,其中90%的数据(138 158个)用于训练网络,5%的数据(7 676个)用于检测网络的泛化能力,5%的数据(7 676个)用于独立评估网络在训练中和训练后的性能。

图9所示为3种不同的数据分配方案训练得到的网络,在GNSS关闭后的2 h内对INS定位修正的误差曲线。

图9 3种训练样本的INS定位误差修正曲线Fig.9 Error correction curve of INS position among three training samples

表3所示为3种不同分配方案训练得到的网络,在GNSS关闭后,对INS定位误差进行修正后的结果。

表3 3种数据分配方案的INS定位误差修正结果Table 3 Position error correction results of INS via three data training distribution schemes

从图9可以看出,用于训练的数据量过少,神经网络拟合INS位置解算与惯性元件测量量之间的数学关系不准确,其表现就是神经网络修正后的INS定位误差规律偏离其一般规律,这一点随着时间的延长愈发明显;训练的数据量过多,神经网络拟合INS位置解算与惯性元件测量量之间的数学关系过于精确,对陀螺仪和加速度计随机误差引起的定位误差缺乏平滑能力,其表现是修正能力持续时间缩短,泛化能力变弱。

4 结 论

船用INS工作时间长,随着时间延长,INS独立工作时的定位误差将快速发散并无法使用。为了延长INS独立工作时保精度的时间,本文使用BPNN模型设计了INS定位预测修正方案,基于Bayesian算法更新网络权重系数。当GNSS有效时,采用组合导航的方式提高系统定位精度,并同步存储INS原始输出数据和GNSS定位结果;当GNSS失效时,利用历史存储数据训练网络参数,将训练完毕的模型用于解算INS位置。结合实船测试的分析结果,可以得到如下结论:

(1) 相比采用L-M算法更新网络权重参数,采用Bayesian算法更新网络权重参数,在训练时间、内存占用、模型计算时间等方面都更具优势,而且能够加强网络对陀螺仪和加速度计噪声的抑制能力,进而提高INS定位修正精度。

(2) 神经元的个数以50为宜,神经元个数过少,容易造成网络欠拟合;神经元个数过多,将造成网络过拟合。欠拟合和过拟合都将导致后续网络修正INS定位的性能下降、持续时间缩短。

(3) 数据集的分配以70%的数据用于训练、15%的数据用于检验网络的泛化能力、15%的数据用于评估网络性能为佳。训练数据偏少将会造成对INS解算的数学模型拟合不足,导致网络解算INS的定位误差不符合规律;训练数据偏多将造成对INS解算的数学模型拟合过于确定,导致网络对陀螺仪和加速度计噪声平滑效果下降。

通过采用上述方法,可以延长INS保精度时间至少2 h。相比INS独立采用实际的数学物理模型解算位置,定位误差均值下降63%,误差最大值下降约50%,最小值下降至0 m。