基于双重反馈的水炮射流稳定系统

程博森，杨 光，蒋奇泽

基于双重反馈的水炮射流稳定系统

程博森1，杨 光2，蒋奇泽2

（1. 武汉船用电力推进装置研究所，武汉 430064；2. 大连测控技术研究所，辽宁 大连 116001）

在海上执法的过程中，执法船只经常会遭遇风浪，而风浪带来的船体晃动会导致水炮晃动，使水炮射流无法准确命中目标。现有的水炮系统多采用单反馈控制方法，没有考虑到载体运动对水射流的干扰。为了减轻载体运动对水炮射流的干扰，本文提出了一种基于双重反馈的水炮射流稳定系统。该系统利用IMU采集载体运动姿态，利用自回归滑动平均模型对载体姿态进行补偿；利用摄像机采集射流落点信息，通过反向传播算法实时调整射流模型参数，并对水炮关节角度进行反馈调整。在智能水炮平台上的实验结果表明，采用双重反馈机制后，水炮的射击误差可有效降低33%以上。

视觉反馈；载体运动反馈；水炮射流稳定；智能水炮；闭环控制

0 引言

水炮系统的发展经历了三个阶段：手动控制、电动控制和自动控制。1944年，美国的Antonio R. Marchese等人发明了固定式手操射流装置，利用蜗轮蜗杆控制水炮的旋转[1]，奠定了现代双轴水炮的雏形。1956年，美国的Edward Z.发明了一种遥控喷射炮塔，用电动马达代替人工来进行驱动[2]，使水炮走向电控时代。2009年，大连海事大学的李鑫设计开发了一种无线遥控水炮控制系统[3]，该系统采用手动遥控的形式来控制水炮的射击操作。2016年，大连理工大学的杨亚飞设计了一种开环控制系统，该系统能够完成水炮的变速旋转、目标跟踪和自动射击等操作[4]，具有一定的自动射击目标的能力。2020年，中国矿业大学的林达设计开发了一种具备视觉反馈的闭环自动控制系统[5]，但该系统没有考虑载体运动对射流轨迹的影响。2016年，陈学军等[6]对消防水炮射流进行建模并作了定位补偿，提高了水炮的定位速度和精度。王冬月[7]将红外技术应用于射流定位补偿，构建了闭环水炮控制系统。Zhu J等[8]利用反向传播技术调整射流模型，提高了射流模型的泛化能力和射击精度。然而，现有水炮系统的反馈调整过程只考虑了风速、泵功率、炮口形状等因素对射流轨迹的影响，没有考虑在外界因素影响下载体姿态变化对水炮射流系统的影响。本文结合视觉反馈和载体运动反馈，设计了一种基于双反馈机制的射流稳定系统，有效降低了载体运动干扰和外界因素干扰带来的影响，提高了水炮系统运行的稳定性。

图1 射流稳定系统控制框图

1 射流稳定系统设计

1.1 射流稳定系统的设计思路

射流稳定系统的控制框图如图1所示。该系统利用摄像机采集目标信息和射流信息，并发送至控制台内的工控主机进行数据处理，计算射流落点和目标位置之间的偏差，再根据偏差来计算和调整步长。此外，系统通过IMU（Inertial Measurement Unit，惯性测量单元）采集载体运动数据并构建误差补偿模型，对采集到的载体运动数据进行补偿，以此获得更准确的运动数据。

基于双重反馈机制的射流稳定方法根据射流落点的偏差计算和调整步长，结合载体运动数据计算水炮各关节电机的转角，然后控制水炮调节姿态以抵抗外部干扰，达到稳定射流的目的。

1.2 载体运动反馈

载体运动反馈由载体运动数据采集和数据调整补偿两部分构成。该系统利用IMU来采集载体运动数据，而IMU采集的数据通常需要进行误差补偿。这些误差一般被分为确定性误差和随机误差[9]。

1.2.1 确定性误差补偿

确定性误差通常包括设备安装误差和内部误差，因此需要计算安装误差系数和IMU校准系数，并构造校准参数矩阵[10]。

IMU的组成如图2所示。

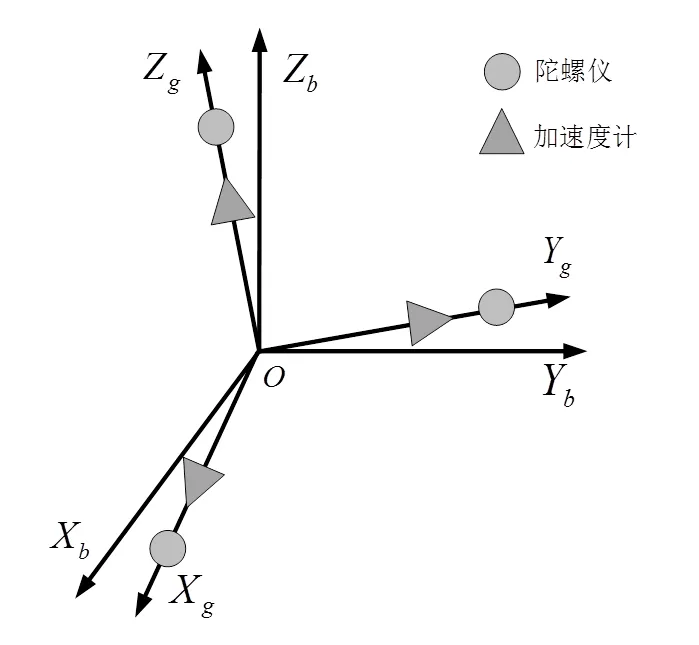
图2 IMU安装图

当载体坐标系绕X轴、Y轴、Z轴旋转的角度已知时，IMU的坐标系可由式(1)推出：

式(2)中，S，S，S为IMU的校准系数，而K，K，K，K，K，K为安装误差系数。

1.2.2 随机误差补偿

本文采用ARMA-KF方法来进行随机误差补偿[11]。卡尔曼滤波算法中估计量的变化规律可通过状态方程来进行描述。假设k时刻的估计状态为X，系统噪声序列为W，则系统状态方程为：

根据最小均方误差准则，可得到如下6个卡尔曼滤波的基本方程：

预测方程：

滤波方程：

增益方程：

预测误差：

估测误差

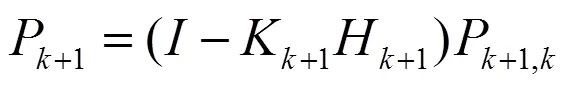
从公式(4)-(9)可以看出，当给定初值0和0时，可以根据时刻的测量量k递归得到时刻的状态估计k。应用卡尔曼滤波的困难在于难以估计随着环境变化而变化的运动状态方程，但ARMA通过对相应数学模型的分析和研究，可以更好地从根本上辨明这些动态数据的内在结构和复杂性。通过将误差ARMA模型转化为卡尔曼滤波所需的状态空间模型，可以提高卡尔曼滤波在实际工作场景中的稳定性。

ARMA()模型可通过式(10)进行描述：

其中：为AR()模型的阶数，为MA()模型的阶数，它们共同组成了ARMA(,)模型的阶数；i为自回归模型的参数，j为移动平均模型的参数，ε是测量误差序列，通常可以假设该序列是一个均值为0，方差为δ的白噪声序列。该模型表明，随机过程{i}在时刻的测量值与之前的个测量值和之前的个白噪声有关。当为0时，模型退化为MA()模型，当为0时，模型退化为AR()模型

下面以ARMA(3,2)为例，将ARMA模型与卡尔曼滤波补偿方法相结合，建立基于自回归移动平均模型的卡尔曼滤波器。

根据式(10)，ARMA(3,2)模型的表达式为：

将式(12)、式(13)和式(14)代入式(3)，即可得到ARMA-KF的模型，进行随机误差补偿。

1.3 视觉反馈

在水炮坐标系中，可以通过分析水炮与目标G之间的坐标关系，采用几何分析法计算射流的偏差角。水炮与目标G的坐标关系如图3所示：

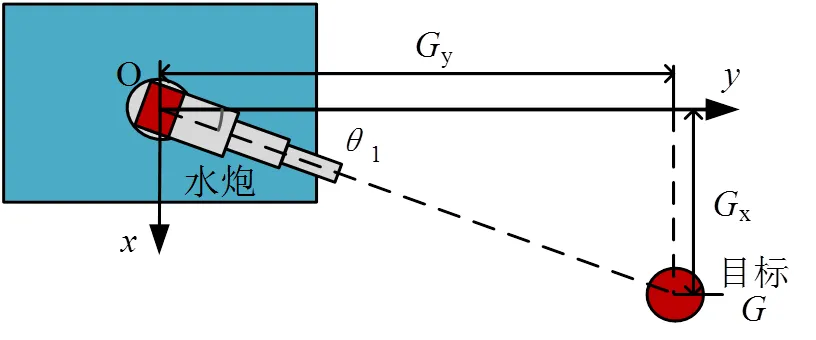
图3 水炮与目标位置关系俯视图

当水炮锁定目标准备射击时，坐标系原点O、枪口和目标中心三点共线。此时，炮管和轴之间的角度即为射流偏差角1。根据图3所示的几何关系，偏差角的计算公式为：

水炮的俯仰角则利用射流预测模型来进行计算，该方法分为两个阶段：利用Matlab离线拟合非线性函数以及基于反向传播算法的在线参数调整方法[12]。

第一阶段，用Matlab离线拟合非线性函数：

式(16)中，为射流落点到水炮坐标系原点的垂直距离。

第二阶段，基于反向传播算法的在线参数调整方法：对射流落点进行实时监测，计算其与目标之间的状态关系，并根据状态关系利用反向传播算法实时计算调整预测模型函数的参数，提高模型精度。

反向传播算法的步骤包括构造损失函数，计算损失函数对模型参数的导数，以及使用梯度下降法更新模型参数[15]。具体步骤如下:

步骤1：构造损失函数。用表示目标与水炮的距离，将其代入式(16)，可以得到此时理论上的俯仰角为：

根据需要的调整方向，构造一个固定的损失角来调整射流模型，定义=0.1°，则实际需要的俯仰角调整角度为：

损失函数的表达式为：

步骤2：计算损失函数对模型参数的导数。

由式(19)易得：

将式(16)中的参数表示为向量形式：

根据矩阵的求导法则，可得：

为了求出损耗函数对参数的导数，利用求导的链式规则，将式(20)和式(22)联立，可得：

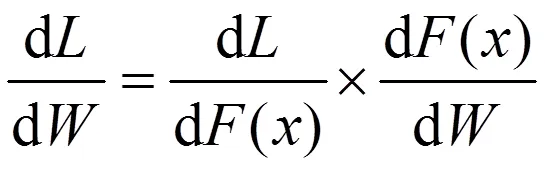
步骤3：采用梯度下降法对模型参数进行更新。根据梯度下降理论，可以根利用(24)在线更新模型的参数，其中lr为反向传播算法的学习率，在本方法中，该参数用于设置调整俯仰角模型时的步长。

针对环境风、泵功率、机械传动误差等因素影响射流运动规律发生变化的问题，采用上述方法实时调整射流模型，可使射流模型动态适应射流运动规律的变化。

2 实验测试

为了测试本文方法的实际应用效果，搭建了图4所示的智能水炮实验平台，其硬件包括：光电摄像机、水炮、水泵、控制台、六自由度平台。

图4 智能水炮实验平台

目标固定在距水炮直线26 m处，光电摄像机安装高度距水平面为3 m，水炮安装高度距水平面2.5 m，目标漂浮，长3 m，宽1 m，高2 m，水炮射程60 m，六自由度平台运动模拟5级海况。实验按以下四步执行：

（1）发射水流对目标进行打击，测量并计算射流落点与目标区域之间的相对误差。

（2）将载体姿态扰动信号加载到六自由度平台上，测量并计算射流落点与目标区域之间的相对误差。

（3）启用载体运动反馈，测量并计算射流落点与目标区域之间的相对误差。

（4）启用视觉反馈，测量并计算射流落点与目标区域之间的相对误差。

本文采用平均绝对偏差（MAD）作为评价指标，该指标可以避免误差相互抵消的问题，能够准确反映实际预测误差的大小。其计算公式为：

误差数据i通过测量获取，()为参考值，本文中设置为0。

2.1 射击误差对比

水炮射击误差数据记录如下：

表1 水炮射击误差对比表

从表1可以看出：采用双重反馈稳定方法于不采用稳定方法使射流落点误差减小了约54%；比采用模型定位补偿法使射流落点误差减小约33%。

2.2 实验效果展示

水炮射击实验的俯瞰效果如图5所示：

图5 不同工况下的射击效果俯瞰图

从图5(a)和(b)可以看出，当载体开始运动时，射流受到明显干扰，射击精度下降，射流落点相对于目标的误差增大。由图5(c)和(d)可以看出，启用双重反馈机制后，与未启用双重反馈机制时相比，射流落点与目标之间的误差明显减小。

3 结论

本文将载体运动反馈与视觉反馈相结合，构建了一种基于双重反馈机制的射流稳定方法，根据视觉反馈的射流落点计算调整步长，结合载体运动反馈，计算水炮各关节电机的调整角度，控制水炮执行，达到抵抗外界干扰，保持射流稳定的目的。实验结果表明，基于双重反馈机制的射流稳定方法可以显著降低载体运动过程中的水炮射击误差，减小幅度超过33%。

[1] Ramasubramanian S, Muthukumaraswamy S A, Sasikala A. Fire Detection using artificial intelligence for fire-Fighting robots[C]//2020 4th International Conference on Intelligent Computing and Control Systems (ICICCS). Madurai: IEEE, 2020: 180-185.

[2] Rakib T, Sarkar M A R. Design and fabrication of an autonomous fire fighting robot with multisensor fire detection using PID controller[C]//2016 5th International Conference on Informatics, Electronics and Vision (ICIEV). Dhaka: IEEE, 2016: 909-914.

[3] 李鑫. 遥控消防水炮系统设计[D]. 大连: 大连海事大学, 2009: 44-60.

[4] 杨亚飞. 水炮控制系统的研发[D]. 大连: 大连理工大学, 2017: 23-48.

[5] 林达. 城市主战消防车自动消防炮研究[D]. 徐州: 中国矿业大学, 2021: 81-94.

[6] 陈学军, 杨永明. 消防水炮射流运动轨迹模型与定位补偿方法[J]. 工程设计学报, 2016, 23(06): 558-563+611.

[7] 王冬月. 红外舰船目标的检测跟踪与射流定位研究[D]. 南京: 南京航空航天大学, 2018: 46-61.

[8] Zhu J, Li W, Lin D. Real-Time Monitoring of Jet Trajectory during Jetting Based on Near-Field Computer Vision[J]. Sensors, 2019, 19: 690.

[9] Du J, Li J. A Compensation Algorithnm for Zero Drifting Error of MEMS Gyroscope[C]//Proceedings of the 2016 5th International Conference on Measurement, Instrumentation and Automation (I CMIA 2016). Amsterdam: Atlantis Press, 2016: 780-784.

[10] 邹泽兰, 徐祥, 徐同旭等. 一种基于改进型自适应遗传算法的MEMS三轴加速度计标定方法[J]. 传感技术学报, 2020, 33(10): 1450-1456.

[11] 陈明明, 高国伟, 毕新磊等. 基于ARMA建模的MEMS陀螺随机误差补偿改进算法研究[J]. 传感器世界, 2014, 20(05): 7-13.

[12] Rumelhart D E, Hinton G E, Williams R J. Learning representations by back-propagating errors[J]. Nature, 1986, 323: 533-536.

Water cannon jet stabilization system based on dual feedback

ChengBosen1, Yang Guang2, Jiang Qize2

(1. Wuhan Institute of Marine Electric Propulsion, Wuhan 430064, China; 2. Dalian Institute of Measurement and Control Technology, Dalian 116001, Liaoning, China)

U661

A

1003-4862（2024）03-0049-05

2023-09-28

程博森（1992-），男，硕士研究生，研究方向：电机控制。E-mail：cbs2266@126.com