基于马斯洛需求理论构建城市吸引力评价模型——以太原市为例

侯娇娜

（山西工程职业学院，山西 太原 030009）

一、引言

“十四五”时期是经济发展换挡提速关键期，人口规模作为生产投入要素刺激产业集聚发展，也作为消费群体释放市场潜力，直接影响城市经济发展。人口集聚为城市带来人口红利，包括劳动力资源、消费动力、创新能力，在新时代新发展阶段下，拥有更多人力资本要素往往意味着有更强的经济增长潜力[1]。同时，城市作为大型人口聚居地，发展水平较高，综合生活成本也相对较高，人口定居或在城市稳定生活的必要条件是具备与城市消费水平相匹配的资本积累能力。人类社会生存必然产生消费需求，而消费是拉动经济增长的“三驾马车”（消费、投资、出口）之一。按照劳动力年龄结构可将人口分为两大类，一类为15～65 岁具备较高劳动力水平的人口，另一类为0～15 岁及65 岁以上不具备劳动力水平或劳动力水平较低的人口。前者反应出城市人口红利水平，是发展贡献的主力军[2]；后者为少年儿童和老人，能够在城市定居或稳定生活说明其家庭或自身具备一定消费潜力，此类群体多为养老、教育、文化、旅游等产业服务对象，也具备刺激新兴市场产生和促进经济发展的正向作用[3]。适龄的劳动力人口流入会产生更为显著的城市建设促进作用，过去一段时间部分城市面向中青年群体的人才落户政策自由度和经济支持力度较大，而针对老年人的落户政策上存在着年龄、子女居住地等条件限制。但是，随着20 世纪60 年代开始的第二次生育高峰期出生人口陆续进入老年阶段，未来中国将进入人口老龄化更为快速发展的时期。不同于以往，当前人民的整体生活质量有了极大的提升，中国社会的主要矛盾转变为人民日益增长的美好生活需要和不平衡不充分的发展之间的矛盾，总体上看，中国老年人消费需求结构也将由生存型需求向发展型和享受型需求升级。同时，在加快构建以国内大循环为主体、国内国际双循环相互促进的新发展格局引导下，市场规模庞大的养老服务相关产业如健康养老服务、养老制造业、养老文旅、养老金融服务以及健康老年人再就业等产业发展将成为一个重要的消费增长点，老年人在城市经济发展内循环中将起到更加重要的作用。同样的，伴随生活水平提升和生育政策放开，未来儿童经济发展也将持续升温，处于消费升级、体验经济和数字经济时代的新一代家长追求儿童成长的全面发展，教育投入成本更高，也为城市经济发展带来了更大市场。因此，对城市来说，人口规模客观上反映了其地区经济发展水平潜力。

近年来，在国家出台多项生育激励政策背景下，中国人口自然增长率仍呈现不断下降态势，2021 年仅为0.34‰。受养育责任大、经济负担重、工作生活难平衡等因素影响，人口增速下降局面在一定时期内难扭转，老龄化现象又日趋严重，甚至有专家预测将迎来人口负增长[4]。2022 年，我国人口自然增长率为-0.60‰，随着经济发展和城镇化步伐加快，伴随生育率持续下降趋势，各城市意识到人口规模增长的重要性，纷纷放开落户政策，开展“抢人大战”。城市人口规模变化呈现出典型的持续性流失或增长的“马太效应”，一些城市人口吸引力较强的地区，人口增速逆势而为，产生虹吸效应，促进城市发展良性循环，给自身发展注入了强大动力，同时另一些城市存在严重的人口流失现象。

合理评估和针对性提升城市人口吸引力水平迫在眉睫。人的行为由一定动机引起，动机源于需求，由此构成“需求-目标-动机-行为”的活动体系。目前主流人类需求理论有马斯洛需求理论、爱尔德弗ERG 理论等，被广泛应用于人类行为动机研究中，如对事物的满意度和获得感、城市宜居性、员工行为激励等[5]。黄江松等（2018）[6]基于马斯洛需求理论构建三级指标体系定量分析探讨城市宜居性。目前城市人口吸引力水平量化评价中，指标体系选取方面以大型机构、学者研究中主流影响因素以及从城市面板数据中挖掘选取两大类为主[7-8]。通常，一级指标多为城市经济、政治、文化、社会、环境等宏观指标，再进一步细化出二级指标构建评价模型，或直接选取如就业收入、公共服务、生活环境等因素作为一级指标构建模型。数据分析处理方面主要有结构方程模型、聚类分析法、因子分析法、主成分分析法、模糊评价法、随机森林法等灵活多样的数据处理方法。综合来看，先前研究虽然意识到城市人口吸引力水平是多种因素共同作用的结果，但仍存在定性分析多、定量分析少，定量分析中指标体系选取系统性、全面性不足，缺少经典理论支撑的问题，少有深度挖掘人的自身需求和进行模型评价结果的验证。

因此，在对城市人口吸引力水平评价中，拟引入社会科学界主流的马斯洛需求理论分析人的自身需求构建指标体系，将城市常住人口作为研究对象构建评价模型并进行回归验证，为增强城市人口吸引力提供可量化的评价依据。

二、模型构建及验证方法

（一）指标体系构建

通过对当前社会科学界主流的人类需求层次理论的分析比较，优选马斯洛需求模型为理论基础，结合相关研究进展，构建出城市人口吸引力评价模型的两级指标体系。其中，一级指标称为“需求层”，共5 个；二级指标称为“条件层”，共30 个。具体内容如表1 所示。需要注意的是，构建的指标体系具有普适性，适用于一般城市，针对特定城市分析人口吸引力水平时要因地制宜，考虑当地实际增补或剔除条件层指标项以完善评价模型。

表1 城市人口吸引力评价模型指标体系表

（二）原始数据量纲化

反映需求层的30 项条件层指标均为量化指标，但其计量单位明显不同。为便于模型构建并进行定量分析，须对原始数据量纲化处理后作为条件层指标数据。根据条件层作用于需求层的倾向不同，数据处理分为两类：可以更好满足需求层的条件层指标进行正向化处理，反之逆向化处理。

正向化处理公式为：

逆向化处理公式为：

公式（1）、公式（2）中，i 为条件层的第i 项指标；Xi为第i 项指标原始数据；为第i 项指标量纲化数据，范围介于0～1 之间；Xi_min、Xi_max 分别为第i 项指标原始数据中的最大值和最小值。

分析条件层的30 项指标，需进行逆向化处理的有：住宅均价、道路交通等效声级水平、工业废水排放总量水平、环境噪声等效声级水平、PM2.5排放水平共5 项。

（三）确定指标权重

1.条件层指标权重确定。根据统计的城市多年份数据，基于主成分分析法赋权，得到各条件层指标权重。主成分分析是数据浓缩、降维处理的方法，将多个指标数据浓缩成为几个彼此不相关的概括性指标（主成分）。

（1）主成分权重：方差解释率除累积方差解释率。

（2）指标权重：第一，计算线性组合系数矩阵，公式为：loading 矩阵/Sqrt（特征根），即载荷系数除以对应特征根的平方根；第二，计算综合得分系数，公式为：累积（线性组合系数* 方差解释率）/ 累积方差解释率，即上一步中得到的线性组合系数分别与方差解释率相乘后累加，并且除以累积方差解释率；第三，计算权重，将综合得分系数进行归一化处理即得到各指标权重值。

2.需求层指标权重确定。需求层指标基于马斯洛需求理论，按生理需要＞安全需要＞归属和爱的需要（社交需要）＞尊重需要＞自我实现需要并结合城市人口特点采用梯度赋值法确权，需求层权重赋值结果如表2 所示。

表2 城市人口吸引力评价指标体系需求层指标权重值

（四）城市人口吸引力水平测算

城市人口吸引力水平测算方法为每层指标体系权重与对应指标层得分或数据相乘，然后相加。具体计算如公式（3）、公式（4）所示。

公式（3）中，AP 为城市人口吸引力水平综合评价得分；n 为需求层指标个数，本研究中取值为5；i为第i 个需求层指标；Wi为第i 个需求层指标对应权重值；Ai为第i 个需求层指标得分。

公式（4）中，im 为第i 项需求层指标下的条件层指标个数；j 为第j 个需求层指标；Wij为第i 个需求层指标下第j 个条件层指标对应权重值；Bij为第i 个需求层指标下第j 个条件层指标得分，其余符号含义同公式（3）。

（五）回归分析验证

采用回归分析法验证构建的城市人口吸引力评价模型是否具有现实意义，验证方法如下：

设由上述模型测算得到的某城市人口吸引力评价综合得分为X，城市年末常住人口数（量纲化数据）为Y，以变量X 为自变量，变量Y 为因变量进行数据回归分析，验证是否存在有意义的回归模型即可判断所构建的城市人口吸引力评价模型是否具有现实意义。

验证回归模型是否存在意义，如针对线性回归模型，可以通过样本代表系数R2、DW 检验值、模型及相关系数的显著性水平（Sig）等相关统计学指标来判断。其中，R2越接近1，模型拟合度越高；查询萨白1977 表判断DW 值区间进而分析模型是否存在自相关；Sig 小于0.05，则拒绝原变量间不相关假设，认为回归方程有意义。

三、太原市人口吸引力水平评价实证分析

按照上述城市人口吸引力评价模型构建及验证方法，对太原市人口吸引力水平进行评价分析，在模型构建中，30 项需求层指标原始数据选取2012—2020 年城市统计年鉴数据。

（一）确定指标权重

太原市人口吸引力评价模型采用指标体系同表1。经过原始数据量纲化（缺失值处理采用均值替代法）、主成分分析法确定需求层、条件层权重如表3 所示。

表3 太原市人口吸引力评价模型指标权重值

（二）城市人口吸引力水平测算

根据式（3）计算得到2012—2020 年太原市人口吸引力评价模型条件层指标得分（见表4）。根据式（4）进一步计算得到需求层指标得分（见表5）。测算得到历年城市人口吸引力综合评分（见图1），可以看出太原市人口吸引力水平逐渐增高。

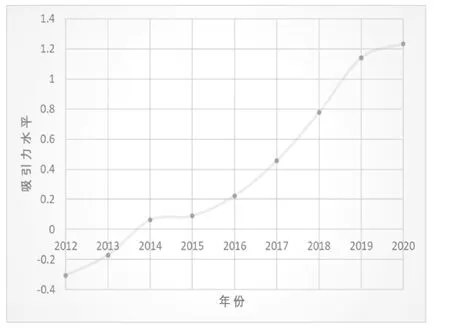
图1 太原市人口吸引力水平值

表4 太原市人口吸引力评价模型条件层指标得分

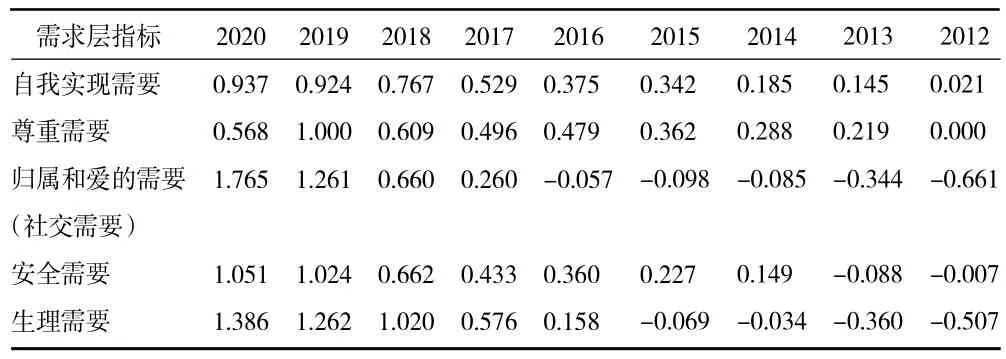
表5 太原市人口吸引力评价模型需求层指标得分

（三）回归分析验证

设由上述模型测算得到的太原市人口吸引力评价综合得分为自变量X，太原市年末常住人口数（量纲化数据）为因变量Y，进行回归分析，构建模型。

1.散点图分析。构建变量间散点图，初步观察自变量X 与因变量Y 之间的关系。可以看出太原市年末常住人口数（量纲化数据）与太原市人口吸引力评价综合得分存在明显的线性关系，适合构建线性回归模型。

2.模型检验分析。进行回归分析得到回归模型：Y=0.627X+0.241，分析模型检验参数表6～表8 可知，模型R2为0.972，接近1，模型拟合度很高；DW值为1.143，查询萨白1977 表得到显著性水平为0.01 时的下界dL=0.554，上界dU=0.998，满足dU＜DW ＜4-dU，判断模型无自相关关系；Sig 小于0.01，则拒绝原变量间不相关假设，认为回归方程有意义。综上所述，构建的线性回归模型有意义，进一步验证了上述方法构建的太原市人口吸引力评价模型有意义。

表6 模型摘要

表7 方差分析

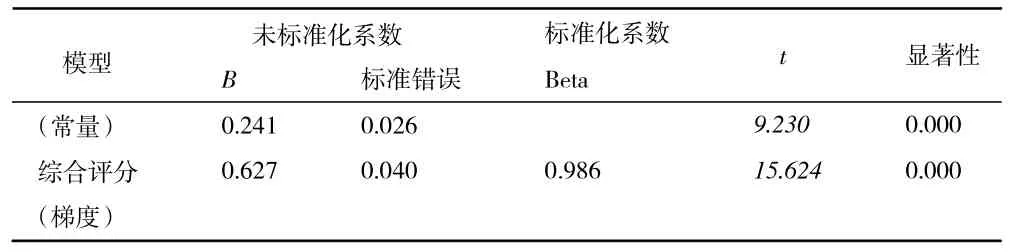
表8 系数检验

四、结论与建议

中国特色社会主义进入新时代，城市高质量发展尤其是经济水平加快提升离不开人的推动，在人口增长率呈逐年下降趋势且短时间内难以扭转的大背景下，增强城市人口吸引力水平，抓住机遇谋发展的需求迫在眉睫。立足以人为本理念，分析人口流动的重要驱动力是人的自身需求，基于马斯洛需求理论从定量角度提出了一种城市人口吸引力水平评价模型的构建及验证方法。评价模型包含需求层、条件层两级指标体系，根据梯度赋值法和主成分分析法确定各级指标权重，结合回归分析法验证模型有效性。该模型可用于不同城市人口吸引力水平评级对比，以及同一城市多年份人口吸引力水平测算自评。

以太原市为例进行实证分析，研究表明：太原市人口吸引力因素中信息互联程度、居民收入储蓄潜力是相对重要的因素，其次为社会保障能力、医疗学校等公共服务配套，权重占比较高。太原市作为国家区域中心城市和省会城市，具有天然的人口吸引力优势，但在人口增速放缓的形势下也需要借助城市建设更好增强人才竞争力。建议在城市发展中加大力度实施智慧城市建设，增强大数据、互联网等信息技术赋能；促进产业转型升级，提供更多高质量就业岗位，提高人均收入水平，增强城市获得感；优化配置公共服务设施，创造优质教育、医疗资源等，增强城市幸福感。通过城市综合环境和治理水平提升，吸引更多常住人口，发挥人口集聚效应，进一步打造I 型大城市，向特大城市奋进，形成良性循环的发展局面。

随着中国人口自然增长率出现负值，为了缓解人口流动行为中两极分化的“马太效应”对经济发展全局带来的不利影响，对于一些人口流入长期呈现正增长的特大型城市或省会城市等，建议未来发展由地区核心城市“一城独大”定位向打造区域双城或多城经济圈、城市群转变，以经济互联互通、产业集约化发展等模式辐射带动城市郊区、周边城市发展水平提升，进一步优化资源配置，提高城市群层面上的人口吸引力水平，由此也能缓解人口过度集中带来的城市住房、教育、环境卫生等公共资源紧张、居民生活压力较高等“城市病”问题，推动地区经济协调均衡发展。总体而言，在城市发展中凸显以人为本的理念，从满足人的生理、安全、社交、尊重、自我实现等方面着手，提高居民幸福指数，打造城市或城市群特色名片，将成为提升人口吸引力水平的根本所在。