SF6气体密度状态检测的快速算法

刘天宇，赵 磊，种佳丽，赵 俊，冯汝明，余 辉，常 敏

（1.内蒙古电力（集团）有限责任公司内蒙古电力科学研究院分公司，呼和浩特 010020；2.内蒙古自治区新型电力系统智能电网企业重点实验室，呼和浩特 010020；3.上海乐研电气有限公司，上海 201802）

0 引言

电力设备的自动化监控对电力系统的安全性非常重要，发展准确性高、实时性好的状态检测算法是监控技术发展的核心[1-5]。SF6气体是一种电负性大、绝缘能力强的介质，在高压电气设备领域得到了广泛应用，作为绝缘和灭弧介质，对高压电气设备和电网的安全具有重要影响。在实际应用中，常常在高压电气设备中充入额定密度的SF6气体来保持设备的绝缘和灭弧能力。但高压电气设备在长期运行中，受各种因素的影响会逐渐发生SF6气体泄漏，甚至发生低温液化，导致高压电气设备的绝缘和灭弧能力下降。因此，对高压电气设备中的SF6气体状态进行检测监控是电力设备维护中的一项重要任务[6-9]。

目前，对高压电气设备中的SF6气体监测，最常用的办法是检测气体密度的变化。SF6气体被填充至密封的空间中，密度不变时，表明密封良好，没有泄漏或液化现象发生，但在理论和实际中很难设计一种直接测量SF6气体密度的传感器[7-17]。大量的研究和工程试验表明，在一定的条件下，SF6气体的密度、压力和温度存在一定的关系，可以用解析公式进行表征。这样就可以借助于软测量技术，得到一种间接测量SF6气体密度的方法。软测量技术在工业领域应用广泛，是一种借助难测物理量和易测物理量之间的模型关系，通过测量易测物理量，再借助模型计算得到难测物理量的实际值。由于缺乏SF6气体密度传感器，密度成为一个难测物理量，但SF6气体的压力和温度的测量技术十分成熟[18-20]。因此，SF6气体密度的检测可以转换为通过检测SF6气体的温度和压力来实现。在得到SF6气体的温度和压力后，如何快速准确地判断其密度状态，取决于计算模型和计算方法的准确性、快速性和鲁棒性能力[21-25]。本文对现有SF6气体检测方法进行分析，提出一种新的快速检测法，介绍了该算法的实现过程，并与现有算法的实时性进行比较，以期达到快速判断SF6密度状态的目的。

1 现有检测算法

SF6气体密度、压力和温度之间关系的解析模型有很多种，最常用的模型为贝蒂-布里奇曼状态方程（Beattie-Bridgeman Equation of State），表达式为：

式中：P为SF6气体压力，MPa；ρ为SF6气体密度，kg/m3；T为SF6气体温度，K。

由公式（1）可知，P、ρ和T之间存在解析表征关系，只要选择好系数，采用较高的计算精度，就能在目前高压电气设备使用的气体密度范围和工作环境温度范围内保证密度的测量相对误差小于1%。SF6气体检测装置可通过传感器采集SF6气体的P和T后，将其代入公式（1），得到一个关于ρ的一元三次方程，采用数值计算方法求解出ρ，然后根据ρ的变化来判断SF6气体是否存在泄漏。电力工业中，高压电气设备中SF6气体的密度，一般是采用标准温度（20 ℃）的压力值P20来表征的。具体检测中，采用贝蒂-布里奇曼状态方程求得SF6气体的密度后，还需进行压力换算，以此作为当前密度的表征值。

软测量过程较复杂，在检测过程中需要不断进行复杂系数的一元三次方程求解运算，以及求解后的等效转换运算，因此SF6气体检测装置对计算能力的要求较高，对于简单的、计算能力弱的CPU 集成电路芯片不适用。基于这些因素，本文提出一种更为简单的、判断SF6气体密度状态的快速检测算法。

2 快速检测算法

分析式（1）可知，当ρ确定后，P和T呈线性关系。高压电气设备出厂时，SF6充气密度的初始值是确定的，在实际运行过程中，应关注密度的变化。现有的检测算法通过模型计算来获取每个时刻SF6气体密度的实际值，再和初始值或设定的阈值进行比较，判断SF6气体是否存在泄漏。SF6气体密度状态监测中关注的是密度的变化而不是密度值本身，密度值是用于比较判断的依据，因此，可以构造一种新的判断算法，不需要SF6气体当前的密度值，只需要对SF6气体的密度变化做出准确的判断，这样能够简化算法，避免大量计算。简化SF6气体密度检测装置的计算复杂性，可以为电力系统中大量应用的电子式SF6气体密度继电器等设备的研制提供一种新的技术思路。该算法的计算过程如下。

（1）确定SF6气体密度的初始额定值ρ0和密度检测的精度要求；

（2）根据密度检测精度要求，确定密度检测结果的上下限，如3级精度，则密度检测的下限是0.97ρ0，上限是1.03ρ0，从而得到上下两个密度限值；

（3）当密度一定时，压力和温度呈线性关系，可以在离线情况下，根据额定密度值和上下限密度值确定3条直线，依次标为下限、额定值和上限；

（4）实际上SF6气体在20 ℃时额定充气压力一般小于1 MPa，设备工作的环境温度范围一般为-40～80 ℃，在这个温度范围内压力变化在0.3～0.9 MPa，因此在这个矩形范围内考虑问题，就可以满足实际应用需要；

（5）如果P 和T 在上述矩形范围内，则密度也在额定值的误差范围内，否则表示越界。

这个算法在实际应用中，只需确定温度和压力的两条临界线段，即可判断SF6气体密度变化是否超标，避免了计算SF6气体密度后再进行判断所导致的运算复杂性。

3 应用举例

对于SF6气体的密度用20 ℃时的压力来表征时，该气室初始密度的压力额定值为0.55 MPa，当表征密度的压力值处于0.55 MPa 附近的误差范围时（一般要求3%的检测精度），表示无泄漏；当由于SF6气体泄漏，表征密度的压力值变为0.50 MPa 时，就需要给出告警信号；当气体进一步泄漏，表征密度的压力值降低为0.48 MPa 时，就要发出闭锁信号，禁止气体绝缘金属封闭开关设备操控动作并需要及时补气。可以看出，SF6气体密度状态监测，重点关注的是状态变化，而非密度本身。

图1为220 kV气体绝缘金属封闭开关设备灭弧室外其他气室（简称GIS 其他气室）的SF6气体压力和温度变化曲线，可以看出，当SF6气体密度确定后，其T和P呈线性关系，密度不同导致线性关系式的特征斜率和截距不同。但是，结合式（1）可知，由于斜率和截距与密度成非线性关系，因此不同密度直线间所夹的区域并非均匀变化的。如图1 所示，随着温度的升高，不同密度之间的间距逐渐变大；但当变换纵轴和横轴的位置时，随着压力的增大，不同密度之间的间距也逐渐变大，但这时密度大的线段处于下面的位置，这与纵轴和横轴互换前的位置恰好相反。

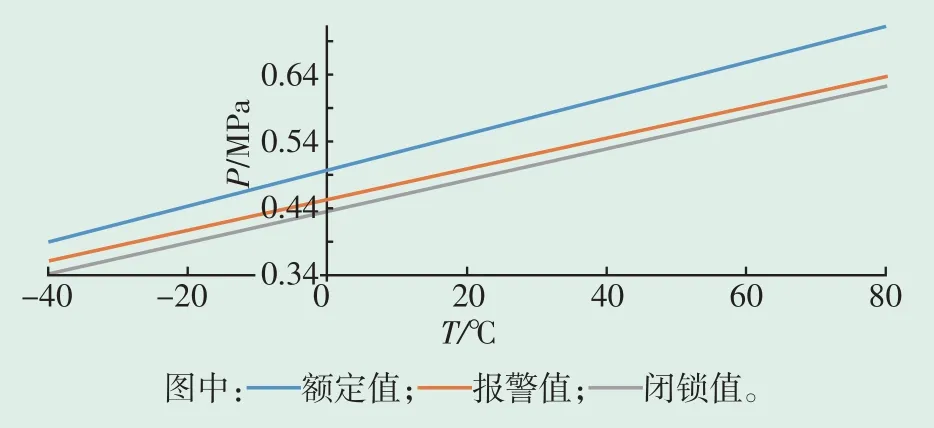
图1 220 kV GIS其他气室SF6气体压力和温度变化曲线Fig.1 Pressure and temperature variation curve of SF6 gas in 220 kV GIS other gas chambers

生成220 kV GIS 其他气室表征SF6气体密度的压力额定值、报警值和闭锁值的判定依据如下。

（1）假设密度的检测精度需要达到3 级，即检测的正负偏差绝对值不超过额定值的3%。表征SF6气体密度的额定值、报警值和闭锁值分别为0.55 MPa、0.50 MPa 和0.48 MPa，根据3%的精度要求，计算确定表征密度的压力上下限值，结果见表1。

表1 220 kV GIS其他气室表征SF6气体密度状态的中心值及其误差限值Tab.1 Center values and error limits for characterizing the density state of SF6 gas of 220 kV GIS

（2）根据3%精度要求确定表征密度的压力额定值、报警值和闭锁值的上下限，将压力值和20 ℃温度条件代入式（1），得到相应的9 个密度值，结果见表1。

（3）将表1的直接密度值代入式（1），可得到额定值、报警值和闭锁值的中心线以及上下误差线的方程式（2）—（10）（为了提高表征方程的有效位数，将压力作为自变量，温度作为因变量）。

与额定值对应的方程式：

与报警值对应的方程式：

与闭锁值对应的方程式：

（4）绘出上述9 个方程对应的直线，如图2 所示，分别为额定值、报警值和闭锁值的中心线及其上下偏差直线。其中在每一组3 条直线中，中间的直线是温度和压力变化过程中的中心线，上面直线误差为-3%，下面直线误差为3%。

图2 220 kV GIS其他气室表征SF6气体密度状态额定值、报警值和闭锁值的中心线和误差线Fig.2 Center lines and error lines characterizing rating value, alarm value and blocking value of SF6 gas density in 220 kV GIS other gas chambers

由图2（a）可知，当检测压力和温度处于上下两条线夹杂的带状区域内时，可以保证密度检测的误差在拟定的精度范围内（＜3%），表明此时SF6气体基本无泄漏。

由图2（b）可知，当检测压力和温度处于上下两条线夹杂的带状区域内时，可以保证密度检测的误差在拟定的精度范围内（＜3%），表明此时SF6气体密度接近报警值附近，存在一定的泄漏，必须给出报警信号。

由图2（c）可知，当检测的压力和温度处于上下两条线夹杂的带状区域内时，可以保证密度检测的误差在拟定的精度范围内（＜3%），表明此时SF6气体密度接近闭锁值，泄漏较多，已经开始影响到设备及系统的安全运行，必须给出闭锁信号，禁止开关投切等动作，并需及时补充SF6气体。

（5）得到SF6气体状态的判断依据并建立判断方法。从图2可知，本文采用的判断SF6气体密度的方法比较简单，可以在不计算SF6气体密度数值的条件下，有效地判断SF6气体密度的状态。以额定值误差阈值直线来说明本文采用的方法，当P和T满足式（11）时，说明SF6气体密度在额定值附近，基本无泄漏，此时检测的SF6气体的温度和压力坐标夹在图2（a）上下两条线之间。对于SF6气体密度是否临近报警值和闭锁值的判断依据与判断方法此类似。

4 实时性仿真验证

现有算法和本文算法的SF6气体密度检测流程见图3。根据图3 所示的流程，在相同的计算环境中，编制两种思路下SF6气体密度状态判定的算法软件。表2为采用两种算法在同一计算机软硬件环境下，分别在每一个温度和压力点累计循环计算图3（a）和（b）的流程各1000次所用的时间。

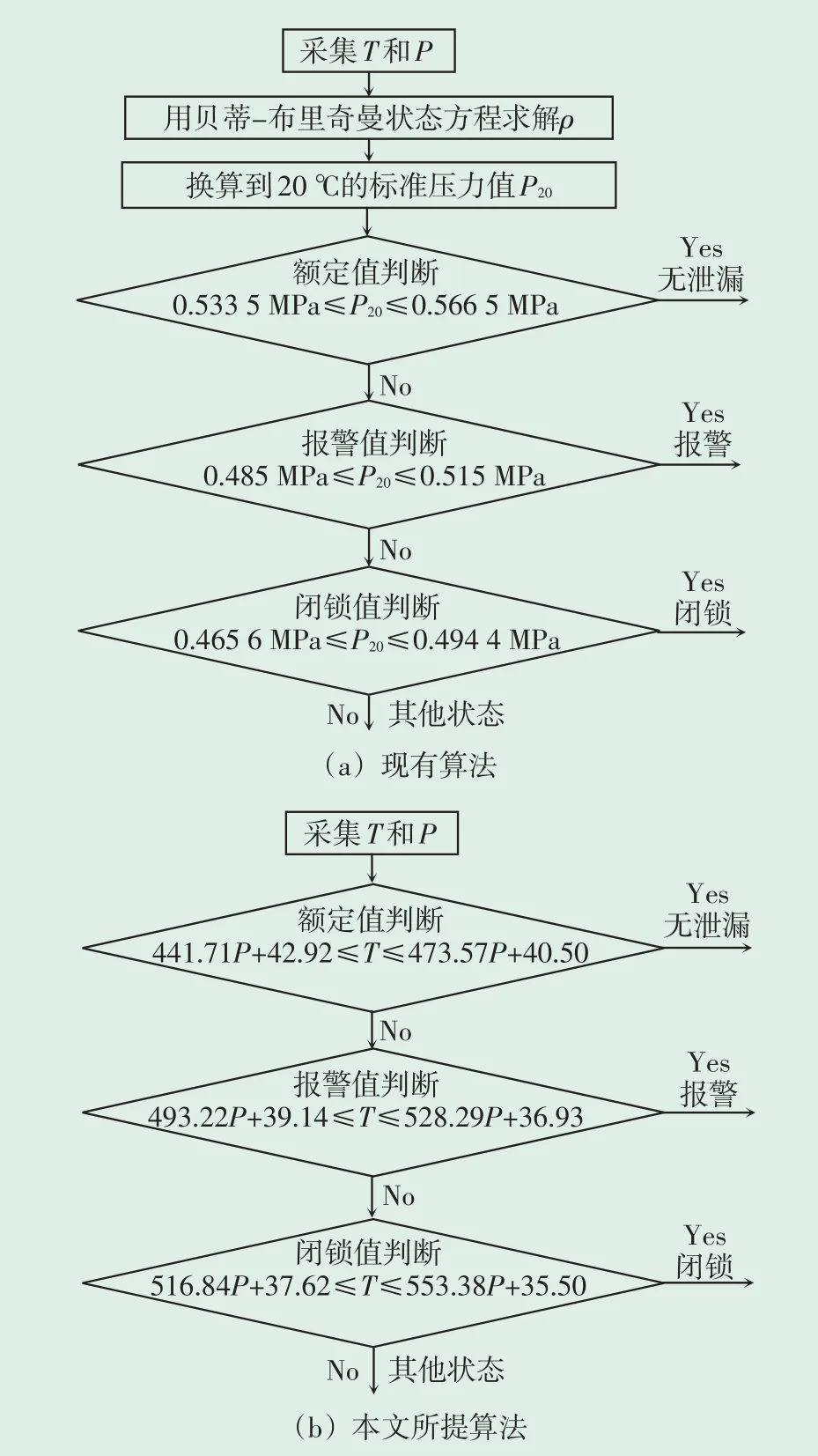
图3 SF6气体密度判定流程示意图Fig.3 Schematic diagram of SF6 gas density determination process

由表2 可知，采用现有算法1000 次运算的时间约50 s，则单次运算用时约50 ms；同样条件下，采用本文算法，单次用时＜1 ms。可见，在同样的计算能力下，本文算法可以大幅提高SF6气体密度判断的实时性，对提高大规模集中检测多个监测点SF6气体密度系统的实时性非常有效。另外，本文算法的判据可以离线准备，然后在线使用，同时计算和编程过程简单，可大幅降低对CPU计算能力的要求。

5 结语

本文针对SF6气体密度状态监测问题，提出了一种新的快速监控的算法，与现有算法相比，可以在规定的检测精度范围内，不需要直接求解计算SF6气体密度数值的基础上，根据SF6气体温度和压力坐标，对SF6气体密度状态做出快速准确的判断。以220 kV GIS其他气室SF6气体密度状态监控点的实现过程为例进行分析，测试了现有算法和本文算法的计算用时，充分说明了该算法的实时性和可操作性。并且，本文算法可以有力支持电力系统中应用边缘计算集中实现智能云监控，同时可以对大量SF6气体密度监测点状态做出快速判断。