吐鲁番地区电网孤网运行的稳控策略
土亚军,胡仁祥,胡 阳,沈志伟,王明慧,曹永吉
(国网吐鲁番供电公司,新疆 吐鲁番 838000)
0 引言
吐鲁番地区属于典型的大陆性暖温带荒漠气候,日照充足极端干燥,降雨稀少、大风频繁,吐鲁番电网作为我国重要的能源电力基地和“西电东送”战略最早的送端之一,电网结构坚强,拥有丰富的风能和光热资源,其中风电主要分布在三十里风区和百里风区[1-2],光伏主要分布在七泉湖光伏区、红山口光伏区和库米什光伏区。风电和光伏因其独特的优势,预计2025 年风电装机高达2728 MW,光伏装机高1460 MWp。
由于风能的随机性和波动性,大规模的风电并网会影响电网动态稳定特性[3-7],近年来,对风电并网的研究较多,但对电网孤网运行下的稳控策略研究较少。本文采用仿真和理论相结合的方法,基于特征值分析法[8],分析在孤网运行情况下,通过对比选取最优振荡模态,采取稳控策略使电网在最短时间内趋于稳定,并提出提高吐鲁番电网动态稳定特性的措施。
1 双馈风机模型
图1为双馈风机并网结构图,由图1可知,风力机通过叶轮将风能转化为机械转矩,机械功率经过传动链推动发电机旋转并产生电磁功率,一部分电磁功率通过发电机定子侧直接向电网传输,一部分电磁功率通过转子侧变换器与电网侧变换器向电网馈电或从电网吸收功率,因此,转子侧变换器用于调节风机输出的有功功率和无功功率,定子侧变换器用于保持控制系统的电压平衡。
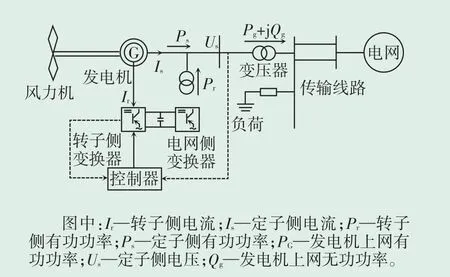
图1 双馈风机并网结构图Fig.1 Grid connected structure diagram of double-fed wind generator
本文忽略转子的谐波分量,只考虑基波分量;忽略磁滞、涡流、铁耗、变频电源的阻抗和损耗,得到双馈风机的等值电路图,见图2所示,该图基于异步电动机等效电路模型图,增加了外接电势源。由双馈电动机的等效电路图可得,双馈发电机的基本方程式如式(1)所示[9]。
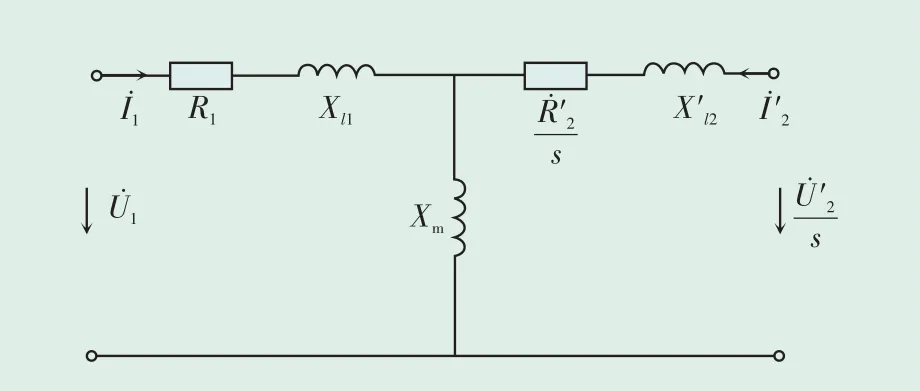
图2 双馈电动机的等效电路图Fig.2 Equivalent circuit diagram of doubly-fed motor
式中:R1、Xl1分别为定子侧的电阻和漏抗;R′2、X′l2分别为转子折算到定子侧的电阻和漏抗;Xm为激励电抗;分别为定子侧的电压、感应电动势和电流;分别为转子侧的感应电动势以及转子电流经过频率和绕组折算到定子侧的值;为转子励磁电压经过绕组折算之后的值;为再经过频率折算后的值;为转子折算到定子侧的电阻再经过频率折算后的值。
2 动态稳定特性
2.1 孤网运行简况
图3为吐鲁番电网结构示意图,由图3可知,吐鲁番电网以750 kV为最高电压等级,以220 kV、110 kV为主干网架,其供电范围东至鄯善七克台镇,西至阿拉沟矿区,南至鄯南南山矿区,北至大河沿镇北部矿区,供电面积达7万km2,同时接入火电厂、水电站、风电场和光伏电站。基于吐鲁番现有网架结构,750 kV 吐鲁番变电站接带负荷为1690 MW,该片区电源总装机为4354.5 MW,其中火电装机为1610 MW,新能源装机为2744.5 MW。新能源最大外送出力为1100 MW。

图3 电网结构示意图Fig.3 Schematic diagram of power grid structure
当新能源大发时,吐鲁番电网多余出力通过750 kV吐鲁番变电站外送,从而保持电网电压和频率平衡。但若吐鲁番变电站1号、2号主变压器故障跳闸,同时什金一二线、柴托一二线热备用将会造成吐鲁番电网局部孤网运行。当新能源出力增加,电网电压、频率随之升高,导致系统发生振荡,为了让电网在最短时间内恢复稳定,需要按一定的比例切除某一片区的风电和光伏出力,因此本文主要通过吐鲁番电网振荡模态图分析切除不同比例风电和光伏下的电网稳态特性。
2.2 振荡模态分析
本文通过特征值分析法分析吐鲁番电网动态稳定特性,求得不同特征值,每个特征值对应某个振荡模态的阻尼情况,特征值λ的表达式如式(2)所示[10-11]:
式中:σ为特征值的实部,w为特征值的虚部。当σ>0时,系统对振荡模态具有正阻尼,系统处于不稳定状态;当σ=0 时,系统对振荡模态具有零阻尼,系统处于等幅振荡状态;σ<0 时,系统对振荡模态具有负阻尼,系统经一定时间的衰减振荡后趋于稳定;w为某振荡模态所对应的振荡角频率,表示该模态下系统振荡的快慢。
当阻尼比小于0.03 时,该特征值所对应的振荡模态为弱阻尼振荡,为了使电网以更短的时间趋于稳定,本文选取阻尼比大于0.03的振荡模态进行分析。特征值对应的振荡模态的振荡频率和阻尼比如式(3)所示:
式中:f为振荡频率;ξ为阻尼比。
为了分析吐鲁番电网孤网运行方式下的稳定特性,提出最优的稳控策略,本文基于PASAP/Prony仿真平台,针对750 kV吐鲁番变电站1号、2号主变压器故障跳闸情况,分别对新能源外送出力为500~950 MW 建立切除不同比例风电、光伏出力情况下的频域仿真模型。电力系统的振荡模态与特征值如表1所示。
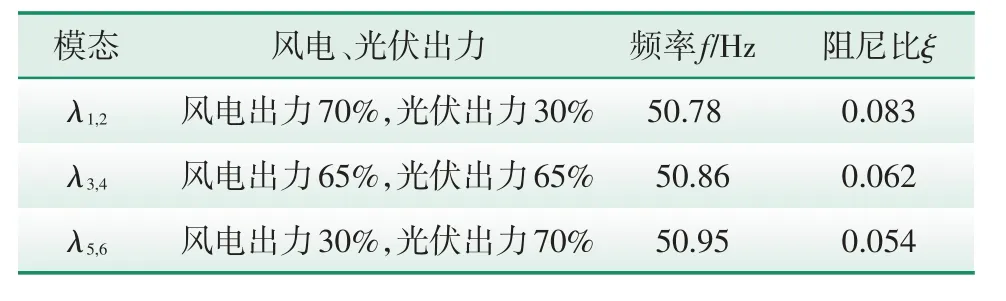
表1 电力系统的振荡模态与特征值Tab.1 Oscillation modes and eigenvalues of power system
图4为各出力下的电网频率图,由图4可知,不同比例的风电、光伏出力均能使电网的频率恢复到允许偏差范围内。但是不同的出力所对应的频率不尽相同,且频率恢复到允许偏差范围内所需要的时间也不同。当风电出力70%、光伏出力30%时,频率变化幅度最小、变化最快,频率在3.48 s内恢复到了50.2 Hz;当风电出力65%、光伏出力65%时,频率变化幅度较为缓慢,频率在4.63 s内恢复到50.2 Hz;当风电出力30%、光伏出力70%时,频率变化幅度较大,变化缓慢,频率在6.85 s时才能稳定到50.2 Hz。

图4 不同出力下的电网频率Fig.4 Power grid frequency under different output
当新能源外送出力为500~950 MW 时,切除风电出力70%、光伏出力30%时,电网频率能在最短的时间内恢复到允许范围内,而当风电出力30%、光伏出力70%时,电网频率恢复到允许范围内所需要的时间最长。
综上所述,为了提高电网的动态稳定特性,当新能源外送出力为500~950 MW 时,本文选择切除风电出力70%、光伏出力30%的策略作为吐鲁番电网孤网运行情况下的最优稳控策略。
3 动态稳定特性改善措施
3.1 电网建设
吐鲁番电网仅有2座750 kV变电站,通过750 kV线路分别与乌鲁木齐电网、哈密电网、巴州电网相连,作为连接新疆主电网以及与东疆电网、南疆电网的枢纽,加强750 kV电网的建设至关重要,在“十四五”规划中需新增750 kV 变电站落点,提高电网断面交换能力,满足新能源送出需要以及大容量火电机组接入系统需要。
近年来,风电、光伏装机占比持续升高,风电、光伏出力参与电力平衡,可以大大弥补火电等常规电源出力不足的缺口,但由于新能源出力的随机性、间歇性以及受网内调峰电源不足等限制,对电网的电压调整、电能质量等具有较大影响,因此,“十四五”期间亟待加强750 kV电网建设[12-18]。
为了提高电网稳定特性,防止出现750 kV变电站全站失压,造成吐鲁番电网局部孤网运行的情况,需优化吐鲁番电网网架,在托克逊片区建设750 kV变电站1座,电网结构图如图5所示。
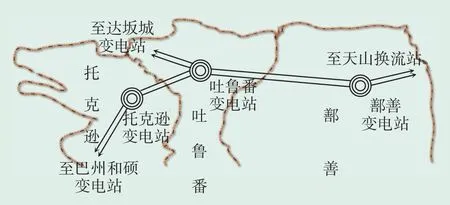
图5 电网结构优化图Fig.5 Optimization diagram of power grid structure
750 kV 托克逊变电站接入吐鲁番电网后,对750 kV吐鲁番变电站1号、2号主变压器同时故障跳闸进行暂态稳定分析,计算结果如表2所示,阻尼振荡模式的阻尼明显提高,说明通过新建750 kV托克逊变电站可以提升吐鲁番电网运行的动态稳定性。

表2 750 kV托克逊变电站投运前后暂稳分析Tab.2 Transient stability analysis of 750 kV Toksun substation before and after operation
3.2 其他措施
对吐鲁番网内机组采取加装电力系统稳定器(Power System Stabilizer,PSS)装置或对机组PSS参数进行优化[18-25],以满足事故后运行方式的需求,尤其是在振荡模式强相关的机组上增设PSS,对于增强阻尼、提高系统动态稳定性效果更为显著。
4 结束语
本文以2022年吐鲁番电网网架结构为基础,通过对比分析不同出力、不同运行模态下阻尼比对电网震荡特性的影响,研究孤网运行情况下的最优稳控策略,以提高吐鲁番电网的动态稳控性。同时提出在托克逊片区新增一座750 kV变电站,解决由于750 kV吐鲁番变电站1号、2号主变压器同时故障跳闸引起的局部电网动态稳定问题。以上结论可为吐鲁番电网局部孤网运行情况下所采取的策略研究提供参考。

