Measuring small longitudinal phase shifts via weak measurement amplification
Kai Xu(徐凯), Xiao-Min Hu(胡晓敏),3, Meng-Jun Hu(胡孟军), Ning-Ning Wang(王宁宁),3,Chao Zhang(张超),3, Yun-Feng Huang(黄运锋),3, Bi-Heng Liu(柳必恒),3,‡,Chuan-Feng Li(李传锋),3,§, Guang-Can Guo(郭光灿),3, and Yong-Sheng Zhang(张永生),3,¶
1CAS Key Laboratory of Quantum Information,University of Science and Technology of China,Hefei 230026,China
2CAS Center For Excellence in Quantum Information and Quantum Physics,University of Science and Technology of China,Hefei 230026,China
3Hefei National Laboratory,University of Science and Technology of China,Hefei 230088,China
4Beijing Academy of Quantum Information Sciences,Beijing 100193,China
Keywords: weak measurement,phase estimation,quantum optics
1.Introduction
Weak measurement, which was first proposed by Aharonov, Albert, and Vaidman,[1]has attracted a lot of attention in the last decades.[2]In the theoretical framework of weak measurements, the system with a pre-selected state interacts weakly with the pointer first and then followed by a post-selection on its state.When the interaction is weak enough so that only the first-order approximation needs to be considered, the so-called weak value of observable ˆA, defined as〈ˆA〉w=〈ψi|ˆA|ψf〉/〈ψi|ψf〉 with|ψi〉 and|ψf〉 being the pre-selected state and post-selected state of the system,respectively,emerges naturally in the framework of weak measurements.[1]The weak value is generally complex, with its real part and imaginary part being obtained separately by performing measurement of non-commuting observables on the pointer,[3]and can be arbitrarily large when|ψi〉and|ψf〉are almost orthogonal.Although the weak value has been intensively investigated since its birth,[4-7]the debate on its physical meaning continues.[8-13]Regardless of these arguments,the method of weak measurement has been shown powerful in solving quantum paradox,[14-16]reconstructing quantum state,[17-20]amplifying small effects[21-25]and investigating foundations of the quantum world.[26-31]
Among the above applications, weak value amplification(WVA)is particularly intriguing and has been rapidly developed in high-precision measurements.In order to realize WVA,the tiny quantity to be measured needs to be converted into the coupling coefficient of a von Neumann-type interaction Hamiltonian,which is small enough so that the condition of weak measurements is satisfied.The magnification of WVA is directly determined by the weak value of the system observable appearing in the interaction Hamiltonian.When the pre-selected state|ψi〉 and the post-selected state|ψf〉 of the system are properly chosen,the weak value can be arbitrarily large.However,the magnification is limited when all orders of evolution are taken into consideration.[32-35]While the potential application of the weak value in signal amplification was pointed out as early as 1990,[36]it has drawn no particular attention until the first report on the observation of the spin Hall effect of light via WVA.[21]Since then, many kinds of signal measurements via WVA have been reported,such as geometric phase,[37]angular rotation,[38,39]spin Hall effect,[21,40-42]single-photon nonlinearity,[43-46]frequency,[47,48]etc.
Despite those progresses in experiments, WMA obtains the large weak value at the price of low detection probability by post-selection, which may cause greater overall error.[49]Therefore, the controversy on whether or not WVA outperforms conventional measurements (CM) arises.[50-55]Several theoretical articles reveal that the post-selection process loses some information, which can reduce the quantum Fisher information (QFI) and result in poorer overall precision than the CM.[56-58]However, advantages arise when practical experiments are taken into consideration.There are some works showing that WMA has the robustness to technical noise.[59-61]Meanwhile,some technical advantages of WVA have been experimentally demonstrated.[62-65]The reason for this contradiction is that the theoretical analysis ignores some practical constraints, which may dominate the error of experiment results.In the experiment, the signal is amplified while the technical noise remains constant.Therefore,the signal-to-noise ratio is boosted by a factor determined by the weak value.[66]There were many attempts of WVA-based proposals for further improvement of the precision, including optimization of pointer states such as squeezing[55]and entanglement,[67,68]the utilization of the recycling technique,[69-72]iterative interactions,[73]and the almost-balanced weak-value amplification technique.[74-76]
Since many physical quantities can be converted into phase measurements,using WVA to realize small phase measurement, especially longitudinal phase, has been developed rapidly.[77-81]However,previous schemes are still not suitable for practical applications because of their severe requirements on the preparation of the initial state of the probe with the continuous degree of freedom and detections on time or frequency domain.The direct amplification of the phase shift in optical interferometry with weak measurement has been experimentally studied by Liet al.[82]The final phase shifts are calculated by scanning the oscillation patterns without and with weak measurement.However, the amplified phase cannot be obtained quickly and their scheme does not apply to the longitudinal phase.Here we propose a different scheme of small longitudinal phase amplification measurement within the framework of weak measurements.Compared with the Sagnac interferometer scheme in Ref.[82],it is universal and can be used in other interferometers like the Michelson interferometer suggested in Refs.[83,84].
In this article, we experimentally demonstrate this new scheme by measuring a small longitudinal phase caused by the liquid crystal variable retarder and realizing one order of magnitude amplification.Besides,the previous theoretical and experimental works do not consider the effect of magnification errors when doing error analysis.In this paper, we add this part and find that the magnification error gradually increases and becomes dominant as the weak value increases.We obtain the trade-off between the weak value magnification and measurement accuracy.
2.Weak measurements based phase amplification
The key idea of weak measurements based small phase amplification (WMPA) is to transform the small longitudinal phase to be measured into a larger rotation along the latitude of the Bloch sphere of the meter qubit, e.g., larger rotation of a photon’s polarization.[83]To explicitly see how it works,consider a two-level system initially prepared in the state of superposition|ψi〉S=α|0〉+β|1〉with|α|2+|β|2=1.Contrary to most discussions of WVA in which continuous pointer is used,[1,2,21,22]we adopt discrete pointer|φ〉P=µ|↑〉+ν|↓〉with|µ|2+|ν|2=1.The pointer can be another two-level system or a different degree of freedom of the same system.We consider a unitary control-rotation evolution of the systempointer interaction

with the successful probabilityPs= Tr[|˜φ〉P〈˜φ|], whereα,β,γ,ηare all taken to be real numbers without loss of generality.Sinceθ ≪1,αγ+βηeiθ ≃(αγ+βη)eiκin the first order approximation with
Since our pointer state is discrete and we do not use the weak interaction approximation exp(-igA ⊗P)≈1-igA ⊗P(the operatorsAandPact on the system and the pointer, respectively), no definite weak value is needed in our case and the magnification is nonlinear.In the traditional standard WVA,the pointer is a wave packet,such as a Gaussian wave packet,which is slightly deformed after coupling.Only through the first-order approximation of the coupling,the shift of the wave packet can be accurately defined.Our scheme uses the polarization as a pointer, and the shift of the pointer angle can be calculated using exact values in theory.Phase signal amplification is realized when the post-selected state is properly chosen such thatS〈ψf|ψi〉S=αγ+βη →0.The normalized pointer state is
in the first-order approximation.Figure 1 shows the schematic diagram of our scheme.Analogous to the micrometer,which transforms small displacement into a larger rotation of the circle, our protocol transforms the small phase into a larger rotation of the pointer along the latitude of the Bloch sphere.The amplified phase informationκcan be easily extracted by performing proper basis measurement on the pointer.It is intriguing to note that the WMPA seems to work even whenS〈ψf|ψi〉S=0,but the approximation of Eq.(3)should be replaced by an accurate one.
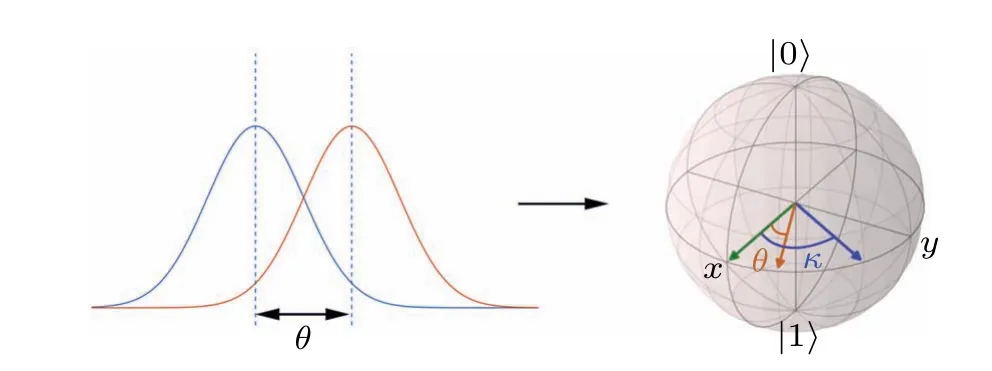
Fig.1.The schematic diagram of our scheme.The longitudinal phase shift θ (the left)is converted to polarization rotation and is amplified to the phase κ (the right).
3.Experimental realization

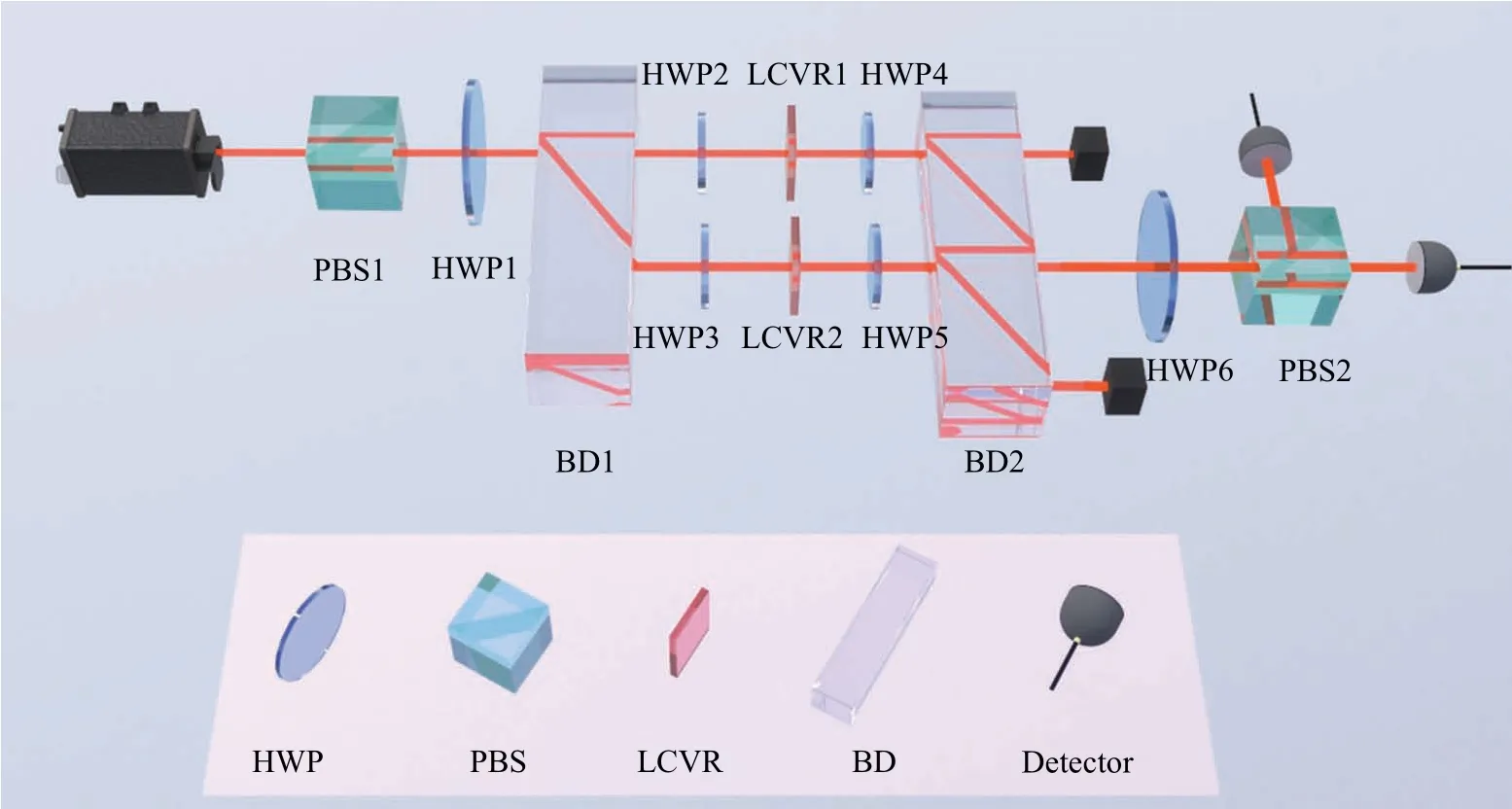
Fig.2.Experiment setup.An attenuated fiber-coupled laser beam is initially prepared in|+〉polarization state by a polarizing beam splitter(PBS)and a half-wave plate(HWP1)rotated at 22.5°.The initial state of the system and the pointer is prepared by a beam displacer(BD)and the HWP2 rotated at 22.5°,the HWP3 rotated at 67.5°,in which the system is the path degree of freedom and the pointer is the polarization degree of freedom.The small phase between horizontal and vertical polarization is produced by the liquid crystal variable retarder(LCVR1)and LCVR2 without voltage added is used for phase compensation.The post-selection of the system is completed by HWP4 rotated at 22.5°-δ,HWP5 rotated at 67.5°-δ and a BD with δ being an adjustable small angle to realize different magnification.The amplified phase signal,which is encoded in the polarization state of the post-selected photons,is extracted by a polarization analyzer consisting of the HWP6 rotated at 22.5° and a PBS.
The whole experimental setup consists of four parts,i.e.,the initial state preparation, small phase signalθcollection,phase signal amplification via the post-selection, and extraction of the amplified phase signalκ.The small phaseθis derived by substituting the measuredκinto the approximation formula of Eq.(3), whereαγ/(βη) is the predetermined experimental parameter.
As shown in Fig.2,the 775 nm laser beam is emitted from the laser.The laser beam has been attenuated before passing through the optical path (it is not drawn in Fig.2), which results in the final counting rate of approximate 8×105s-1.The light beam passes through a polarizing beam splitter(PBS)and a half-wave plate(HWP1)rotated at 22.5°such that the polarization of photons is prepared in the state|+〉.Preparation of the initial state of photons is completed by passing through a calcite beam displacer (BD) and two HWPs (HWP2 and HWP3)placed in the two paths separately.The BD is approximately 39.70 mm long and photons with horizontal polarization|H〉 can transmit through it without change of their path while photons with vertical polarization|V〉suffer a 4.21 mm shift away from their original path.The HWP2 and HWP3 are rotated at 22.5°and-22.5°,respectively,which gives the initial state of photons as,where|0〉represents the state of down path and|1〉 represents the state of up path.In fact, the initial state of the system, i.e., path degree of freedom, and the pointer, i.e., polarization degree of freedom, can be prepared into an arbitrary state via rotating HWP1,HWP2,and HWP3.
The small longitudinal phase signalθto be measured is produced by LCVR1(Thorlabs LCC1411-B)placed in the up path.The LCVR causes a phase shift between the horizontal and vertical polarization states of photons when the voltage is introduced by a liquid crystal controller(Thorlabs LCC25),the calibration of LCVR is shown in Appendix B.Another LCVR placed in the down path without introducing voltage is used for phase compensation.The LCVRs fulfill the unitary operation of a controlled rotation and the state of photons,after passing through the LCVRs,becomes
The amplification of the small phase signalθis completed via HWP4, HWP5, and BD2, where the post-selected photons come out from the middle path of the BD toward HWP6.To see explicitly how post-selection works, we can recast Eq.(5)as
which implies the exchange of the path degree of freedom and the polarization degree of freedom of photons.Since the polarization degree of freedom of photons represents the system now, post-selection of the system can be readily realized by an HWP combined with a PBS.Suppose that the HWP is rotated at 22.5°-δwithδbeing a small angle, then the postselected state of photons coming out from the reflection port of the PBS is|ψf〉=sin(45°-2δ)|H〉-cos(45°-2δ)|V〉.After the post-selection, we exchange back the system and the pointer to the original degrees of freedom by using an HWP rotated at 45°in one of the outgoing paths and a BD to recombine the light beam.The above process of post-selection can be equivalently realized via HWP4 rotated at 22.5°-δ,HWP5 rotated at 67.5°-δand BD2 as shown in Fig.2.

4.Results
Figure 3 shows the relationship between the amplified phaseκand the small phaseθ, in which lines are theoretical predictions and dots are measured data.When the phase signal to be measured is small enough, according to Eq.(3),the factor of amplification is mainly determined by the parameter(αγ)/(βη).Two different values of(αγ)/(βη)are considered in our experiment corresponding to the magnification factors about 4 and 10 with success probabilitiesp=0.0204(δ=0.0716)andp=0.0026(δ=0.0255)respectively in the linear amplification region.For each case, four small phases are chosen in the range between 0.03 rad and 0.08 rad,which are produced by LCVR1 and are measured in advance.

Fig.3.Experimental results of phase amplification.The relationship between the amplified phase κ and the small phase θ which is to be measured.The real lines are theoretical predictions based on Eq.(3)with different colors representing different values of (αγ)/(βη).The dots are measured data.The transverse errors come from the calibration errors and the longitudinal errors are derived from the raw data.

Once the parameter (αγ)/(βη) is settled, the voltage can be added to LCVR to produce a small phase and the amplification measurement can be realized.The small phaseθis immediately estimated by conventional measurement methods after the amplification measurement,which is done by blocking the down path between BDs, replacing HWP4 with an HWP rotated at 67.5°and rotating HWP6 to 45°.Two different values of(αγ)/(βη)are obtained by adjusting the small angleδand four small phases are measured within 30 s counting for each value.Considering the relevant statistical errors, random errors,and imperfections of optical elements,our results fit well with the theoretical predictions.

5.Conclusion
Although we only experimentally demonstrated the amplification of a polarization-dependent longitudinal phase,the general tasks of phase amplification can be readily realized by using Michelson interferometer suggested in Refs.[83,84].This realization indicates that WMPA is capable of measuring any small phase signal with higher precision and sensitivity than the CM in practice.
In conclusion, we have described and demonstrated a weak measurements amplification protocol,i.e.,WMPA that is capable of measuring any small longitudinal phase signal.The small phase introduced by LCVR is measured and one order of magnitude of amplification is realized.In our error analysis,the effect of magnification error is considered and we find that there is a trade-off between magnification and error.Larger amplification is possible if we consider cascading scenarios.The WMPA would have higher precision and sensitivity than the CM if the quantum noise limitation is negligible, which is usually the case in practice.In addition, the precision of our scheme has the potential to achieve the Heisenberg-limited precision scaling by using quantum resources such as squeezing states.[55]Our results significantly broaden the area of applications of weak measurements and may play a crucial role in high-precision measurements.
Appendix A:Phase uncertainty
Here we calculate the phase uncertainty of our scheme.Considering a realistic interferometer, the detection probability is

However, Ref.[82] does not consider the uncertainty of magnification factors.As previously mentioned,the factor of amplification is mainly determined by the post-selection probability which is related toδ.The phaseθ ≃4δκ.According to the error transfer function,the phase uncertainty becomes
Appendix B:The calibration of the liquid crystal variable retarder
Project supported by the National Natural Science Foundation of China (Grant Nos. 92065113, 11904357, 62075208,and 12174367), the Innovation Programme for Quantum Science and Technology (Grant No. 2021ZD0301604), and the National Key Research and Development Program of China (Grant No. 2021YFE0113100). This work was partially carried out at the USTC Center for Micro and Nanoscale Research and Fabrication. Meng-Jun Hu is supported by Beijing Academy of Quantum Information Sciences.
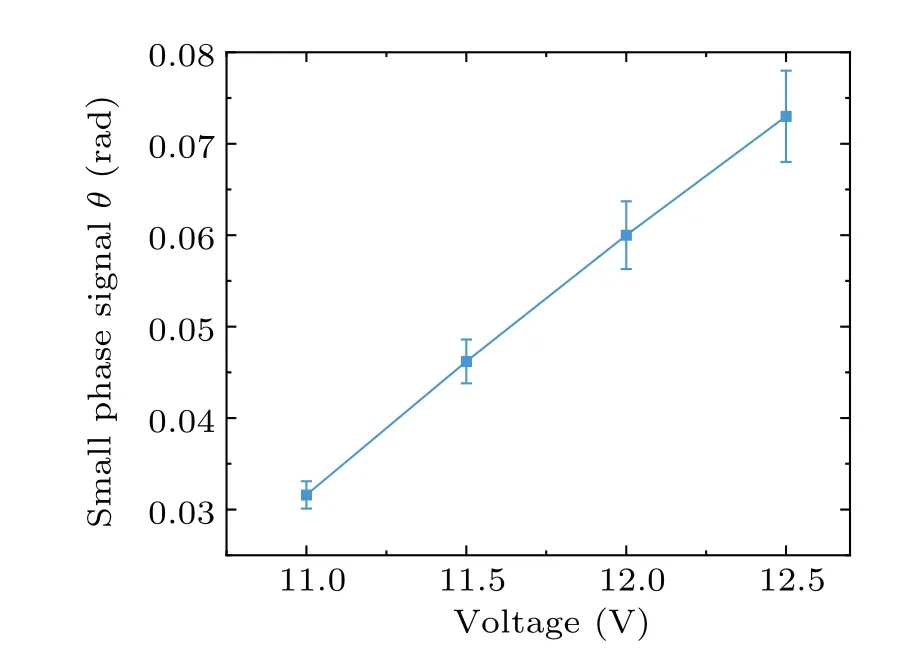
Fig.B1.The calibration curve of the LCVR.
Acknowledgements
Project supported by the National Natural Science Foundation of China (Grant Nos. 92065113, 11904357, 62075208,and 12174367), the Innovation Programme for Quantum Science and Technology (Grant No. 2021ZD0301604), and the National Key Research and Development Program of China(Grant No. 2021YFE0113100). This work was partially carried out at the USTC Center for Micro and Nanoscale Research and Fabrication. Meng-Jun Hu is supported by Beijing Academy of Quantum Information Sciences.
- Chinese Physics B的其它文章
- Does the Hartman effect exist in triangular barriers
- Quantum geometric tensor and the topological characterization of the extended Su–Schrieffer–Heeger model
- A lightweight symmetric image encryption cryptosystem in wavelet domain based on an improved sine map
- Effects of drive imbalance on the particle emission from a Bose–Einstein condensate in a one-dimensional lattice
- A new quantum key distribution resource allocation and routing optimization scheme
- Coexistence behavior of asymmetric attractors in hyperbolic-type memristive Hopfield neural network and its application in image encryption

