Tunable spectral continuous shift of high-order harmonic generation in atoms by a plasmon-assisted shaping pulse
Yuan Wang(王源), Yulong Li(李玉龙), Yue Qiao(乔月), Na Gao(高娜),Fu-Ming Guo(郭福明), Zhou Chen(陈洲), Lan-Hai He(赫兰海),†,Yu-Jun Yang(杨玉军),‡, Xi Zhao(赵曦), and Jun Wang(王俊),¶
1Institute of Atomic and Molecular Physics,Jilin University,Changchun 130012,China
2Jilin Provincial Key Laboratory of Applied Atomic and Molecular Spectroscopy,Jilin University,Changchun 130012,China
3Beijing Institute of Space Launch Technology,Beijing 100076,China
4School of Physics and Information Technology,Shaanxi Normal University,Xi’an 710062,China
Keywords: high-order harmonic,semi-integer-order,spectra shift,inhomogeneous field
1.Introduction
High-order harmonic generation (HHG)[1-9]serves as a potent avenue for generating coherent radiation in the short-wave spectrum, with applications extending from the infrared to the XUV and even the soft x-ray range (1-30 nm).[10-12]This property makes high harmonics an invaluable source of light, particularly for producing attosecondduration pulses.[13,14]
The mechanism behind HHG can be comprehended through the semi-classical three-step model.[15]It commences with the depression of atomic potential under the influence of the electric field, allowing electrons to tunnel through potential barriers.[16]Subsequently,electrons move freely within the electric field,and a subset of electrons have the opportunity to emit high harmonics by recombining with the parent ions as the electric field reverses.This emission process hinges upon the time-domain characteristics of the laser field and can be manipulated to achieve spectral tuning.
Previous methods of spectral tuning have been demonstrated to be successful, such as using laser chirp conditions[17-19]and controlling the carrier-envelope phase.[20-23]However, these approaches are often complex and offer limited tuning ranges.Spectral gating methods,like polarization gating,[24]have also been explored to extend the HHG platform.Recently, the utilization of spatially inhomogeneous fields[25]generated by irradiating specific metal nanostructures with femtosecond laser pulses has emerged as an effective HHG technique.This approach capitalizes on the spatial gradient of the inhomogeneous field, enabling ionized electrons to attain higher energies and significantly extending the harmonic cutoff position.[26]Furthermore, the unique spatial properties of the inhomogeneous field impact electron motion and contribute to the HHG process[27,28]often resulting in the generation of even harmonics due to the spatial symmetry breaking.[29,30]Therefore,the intricate interplay of intense laser pulses with matter gives rise to a rich tapestry of nonlinear phenomena, with high harmonics serving as a versatile and powerful tool for generating coherent short-wave radiation.The novel utilization of spatially inhomogeneous fields offers an exciting avenue for further advancing HHG technology, providing new opportunities for spectral control and modulation.
The ability to achieve spectrally tunable HHG with adjustable photon energies holds significant importance for various experimental applications, such as angle-resolved photo emission spectroscopy and lifetime measurements of excited atomic or molecular states.These experiments often require a narrow wavelength range for excitation.To address this requirement, Oldalet al.proposed a method involving double pulses to generate higher-order harmonics with tunable photon energies and spectral widths.[31]Spectral tuning involves shifting the frequency of the HHG spectrum.This frequency shift is attributed to two main factors: the rapidly varying envelope effect of ultrashort laser pulses and the propagation effect.When the laser pulse intensity and atom density are relatively low, the propagation effect can be neglected.For instance, in the case of a Gaussian pulse, electrons gain more kinetic energy from the laser electric field during the rising part of the pulse,leading to a blue shift in the HHG spectrum.Conversely,a red shift occurs during the descending part of the pulse.These effects are analogous to frequency chirp modulation and amplitude chirp modulation.The blue shift in HHG can be achieved using a strong and long laser pulse, and it has been widely investigated theoretically.[32-34]Similarly,red shifts in molecular HHG,which can probe nuclear motion,are of great interest.[35,36]
Interestingly,the simultaneous occurrence of red and blue shifts in atomic HHG has been reported.[37]It investigates the sinusoidal phase shaping pulseφ(ω)=Asin[(ωref-ω)T+φ]under homogeneous field, which has made very good results by the predecessors.However, we found that under homogeneous fields, continuously tuned harmonic spectra cannot be obtained by changing the absolute phase offset(φ).The ability to achieve spectrally tunable HHGs using tunable photon energies is of great importance for various experimental applications.In order to fulfill this requirement,therefore,an inhomogeneous field factor is introduced to improve the tunability of the harmonic spectrum.We investigate the harmonic emission of helium atoms interacting with a plasmon-assisted sinusoidal phase-modulated shaping pulse,compared to the homogeneous field case, because of the incorporation of spatial gradients due to inhomogeneous fields,with further increasing the regulation of the electron trajectories.The modulation of the electric field in the frequency domain not only alters the atomic harmonic spectrum but also introduces a novel method to modify harmonic frequency centers.By adjusting the absolute phase parameter of the incident laser pulse, harmonic wavelength can be continuously tuned.Additionally, semiinteger order harmonics are observed in the harmonic spectrum.Unlike traditional explanations that rely on harmonic absorption and quantum leap theory,[38]it is proposed that these semi-integer order harmonics arise from the interference between multiple back-nucleation electron-emission harmonics.
The work is organized as follows: Section 2 outlines the theoretical model and the numerical methods used in the study.Section 3 discusses the effects of tuning the phase parameter of the incident laser pulse on atomic HHG spectral modulation.Finally,Section 4 provides a concise summary of the findings.Throughout this paper, atomic units are utilized unless specified otherwise.
2.Theoretical model and method
In our theoretical study, we perform calculations on the harmonic emission process of helium atoms under the influence of a plasmon-assisted sinusoidal phase-modulated shaping pulse.To model this process, we consider the one-dimensional (1D) time-dependent Schr¨odinger equation(TDSE) in the length gauge, and we solve it using the splitoperator method.The TDSE can be expressed as
whereRis the position of the atom,V(x,R) =is the soft Coulomb potential of the helium atom with the soft-core parametersZ= 0.6338 anda=0.113, andVE(x,t) is the potential function of the laser field.For a spatially inhomogeneous field,the interaction energy isVE(x,t)=∫x0E(x′,t)dx′.An inhomogeneous electric field can be expressed as the product of a spatial functional part and a temporal functional part:E(x,t) =Es(x)Et(t).The time partEt(t) corresponds to ˜Eoutafter sinusoidal bitphase shaping.We start with a transform limit laser pulseEin(t)=(1/2)E0f(t)eiω0t+c.c.The initial electric field intensity,full width at half maximum(FWHM),and wavelength of the driving laser pulse areE0=0.05, 10 o.c.(optical cycle), and 800 nm.With the Fourier transform, we can obtain the electric fieldEin(ω) in the frequency domain.Further,we could modulate the electric field by adding a phase modulation parameter ˜Eout(ω)= ˜E˙in(ω)eiφ(ω).In the frequency domain,the phase function isφ(ω)=Asin[(ωref-ω)T+φ],whereAdescribes the amplitude modulation function of the phase,Tis the frequency of the sinusoidal oscillations,andφis the absolute phase offset,ωref=0.057.Finally,a new timeenvelope function ˜Eoutis obtained by using the Fourier inverse transform.Different from other phase modulation techniques,this modulation is carried out in the frequency domain,which can greatly regulate the degree of asymmetry of the laser field,while at the same time the central frequency of the laser field remains unchanged before and after the sinusoidal phase shaping.Moreover, the robustness and manageability of this modulation is not achieved by other phase modulation techniques.
Experimentally,the above part is commonly achieved by pulse shaping,with the 4fshaping optical path scheme being one of the most typical laser field shaping approaches.[39,40]The specific device is schematically illustrated in Fig.1.[41]The optical path incorporates two diffraction gratings, two cylindrical lenses, and a liquid crystal spatial light modulator(SLM).As the laser pulse traverses the shaping optical path,it undergoes a Fourier transform from the time domain to the frequency domain through the first grating and the cylindrical lens.Subsequently,the laser polarization direction aligns with the optical axis direction of the liquid crystal array in the SLM.The refractive index of individual pixels in the liquid crystal array is manipulated by applying distinct voltages to the electrode plates at ends of the SLM,inducing variations in the phase of corresponding frequency components.By calculating the projection of the laser electric field on each coordinate axis, we can ascertain the electric field’s changes as it passes through each segment of the liquid crystal spatial light modulator,thus achieving precise modulation of the phase.[42,43]Finally,through the second set of cylindrical lenses and gratings,a inverse Fourier transform is executed to transition from the frequency domain back to the time domain,accomplishing the goal of laser shaping.In experimental settings,various phase functions exist,with the sine phase garnering attention for its capability to generate pulse sequences with specific spacing.
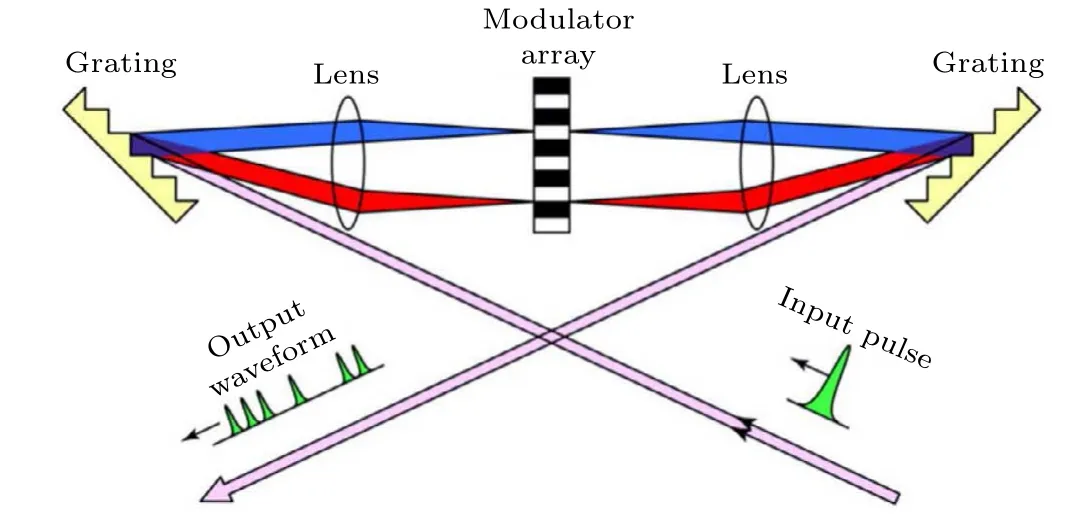
Fig.1.Schematic diagram of 4 f shaping optical path.
For the space functionEs(x)denoted by
in experimental scenarios the spatial field distribution closely resembles the actual conditions, especially when a pulse interacts with a nanotip nanostructure, resulting in the creation of a spatially inhomogeneous field due to resonance effects.The extent of this spatial inhomogeneity can be controlled by the spatial factorε,η, andµ.Additionally, to mitigate the influence of wave packets near the boundary on HHG,a mask function of the form cos1/8is implemented.Subsequently,the time-dependent induced dipole moment is determined using the Ehrenfest theorem,

After thorough investigation,[44]it is evident that the onedimensional program is plagued by the wave packet dispersion issue.However,upon comparison with three-dimensional calculations,it becomes apparent that the harmonic spectra differ primarily in intensity.This work,in particular,concentrates on finely tuning the frequency of the harmonic spectrum.Despite the one-dimensional program’s tendency to over-calculate the ionization rate and harmonic spectrum intensity, the shift in the harmonic order, when compared to the three-dimensional program, appears to have minimal impact.Based on this observation, we confirm that wave packet dispersion is unlikely to significantly influence the harmonic order shift, and therefore, it will not exert a substantial impact on the conclusions drawn in this work.
In order to understand the high harmonic generation process, we also simulate the motion of ionized electrons driven by an intense laser pulse by solving the classical Newtonian equations of motion:
3.Results and analysis
In our theoretical investigation,we have studied the process of harmonic emission from helium atoms under the influence of a plasmon-assisted sinusoidal phase-modulated shaping pulse.Figure 2(a)provides a schematic representation of the laser-atom interaction scenario.The parameters chosen for the sinusoidally phase-modulated pulses in our calculations areA=0.5,T=1400, andE0=0.05.To better approximate the actual spatial field distribution encountered in experiments, we employ an inhomogeneous field expression ofε=12.02,µ=0.8001,η=340.7.Additionally, the nanotip’s position is set at-20 nm in the onedimensional space, while the mask function is positioned at-19 nm.Figures 2(b) and 2(c) illustrate the temporal and spatial profiles of the coupling field, as well as its projected image.It is evident that the inhomogeneous field effect decreases as the distance from the gold tip position increases.Consequently,the coupling field exhibits significant variations in both time and space as the position changes.
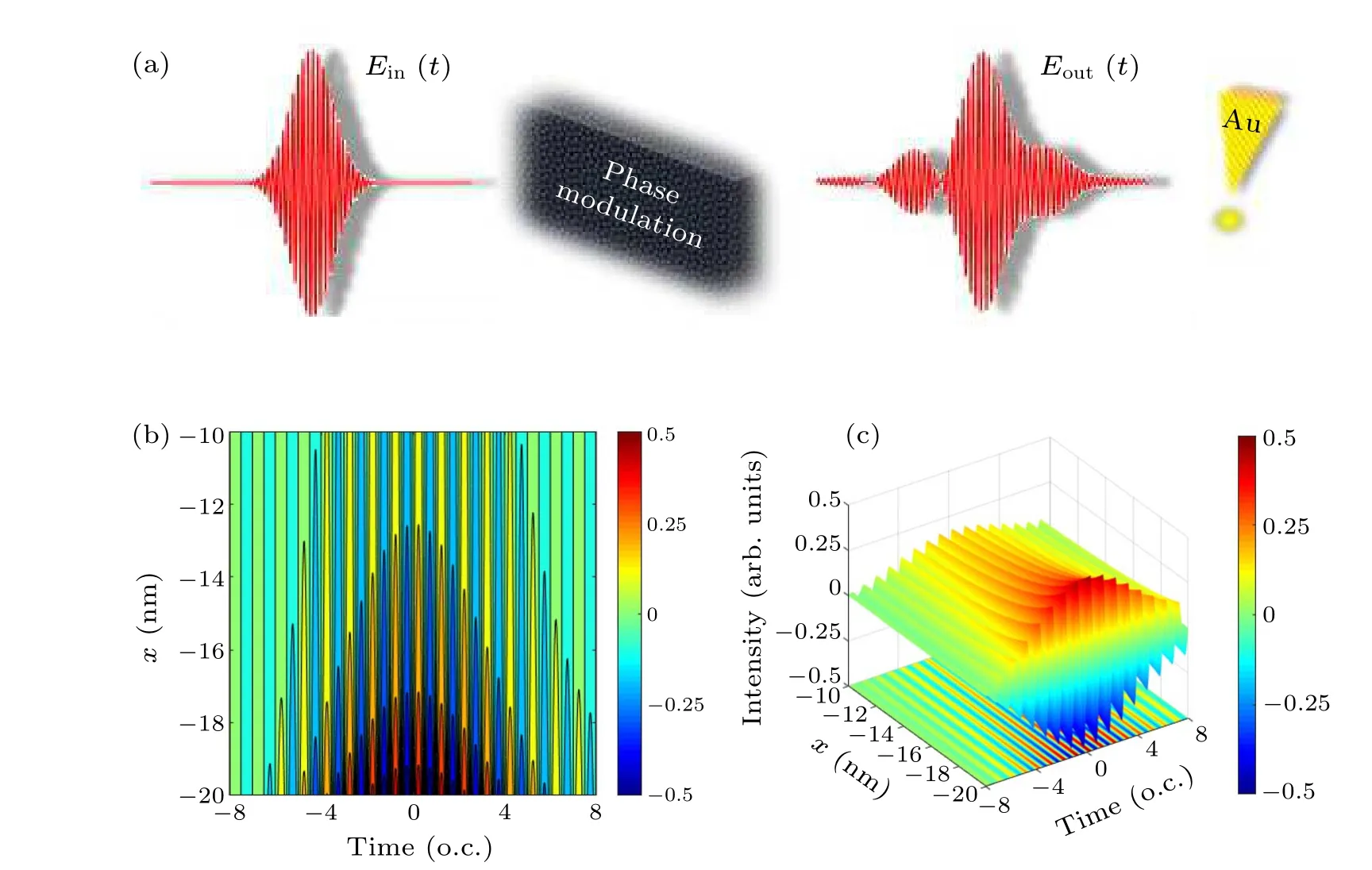
Fig.2.(a) Schematic diagram of laser interaction with helium atoms, (b) projection of simulated field in the space-time plane,(c)schematic diagram of simulated spatio-temporal field.
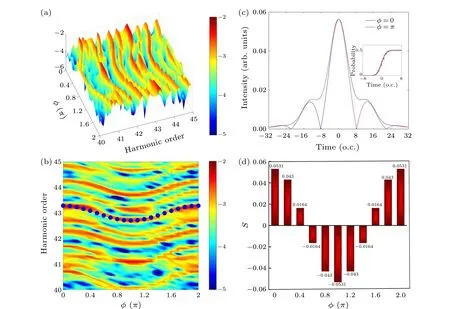
Fig.3.(a)Variation of harmonic intensity with φ.(b)Envelope intensity of sinusoidal phase modulated pulse when φ =0(red solid line)and φ =π (blue solid line).The inset shows the ionization probability of helium atoms.(c)Comparison of the variation of the harmonic intensity with φ and the fitted curve of the asymmetry coefficient.(d)Variation of the asymmetry parameter with φ.
In our investigation, we have delved into the harmonic emission process arising from helium atoms when subjected to plasmon-assisted sinusoidal phase-modulated shaping pulses with different absolute phases in the spatially inhomogeneous field.The resulting variation in harmonic intensities at different absolute phases is depicted in Fig.3(a).This figure portrays the intensity variation of low-order harmonics (40-45 orders of magnitude).Several observations can be made from this figure.Firstly, the harmonic spectrum undergoes a considerable frequency shift asφchanges.The photon energies of the resulting harmonics are controllable within a range of 1.2 eV, with the harmonic frequency shifts symmetrically distributed concerningφ=π.Whenφis very small, a pronounced blue shift in the harmonics becomes evident asφvaries.Conversely, asφincreases overπ, a significant red shift in the harmonics occurs.The blue shift is attributed to the positive chirp induced by the rising part of the laser field,resulting in a spectral blue shift,where dI(t)/dt >0 withIbeing the pulse intensity.In contrast,the negative chirp from the descending part of the laser field leads to a spectral red shift,where dI(t)/dt <0.When the rising and falling parts of the laser field are symmetric, the blue and red shifts could cancel each other, and notable harmonic frequency shifts might not be observed.To further explore the frequency shifts of the harmonic spectrum at differentφvalues, we illustrate the envelope intensity of the sinusoidal phase-modulated pulse atφ=0(red solid line)andφ=π(blue solid line)in Fig.3(b).The rest of the electric field parameters remain consistent with Fig.3(a).It is evident from Fig.3(b)that the pulse comprises a main pulse and two sub-pulses situate at different positions.Withφ=0 the left sub-pulse is farthest from the main pulse,while the right sub-pulse is closest, creating an asymmetric distribution about the midpoint of time.Additionally, the intensity of the descending part of the laser field exceeds that of the ascending part.Asφgradually increases towardsπ, the left sub-pulse moves closer to the main pulse while the right sub-pulse moves away,ultimately the highest degree of envelope symmetry around 0.5π.During this process the intensity of the ascending part of the laser field gradually increases and contributes to the blue shift in the harmonic spectrum.Conversely, asφincreases fromπto 2πthe process inversely mimics the transition fromφ=0 toφ=π, resulting in a red shift in the harmonic spectrum.The degree of asymmetry in the pulse can be quantitatively analyzed by defining the asymmetry coefficient between the ascending and descending parts asThe asymmetry parameters corresponding to differentφvalues are presented in Fig.3(d).It is noted that the asymmetry parameter is 0.0531 atφ=0 and it is-0.0531 asφ=π.The asymmetry parameter decreases whenφgradually increases from 0 toπ,it gradually increases withφincreasing fromπto 2π.Figure 3(c)displays a comparison between the harmonic spectral shifts and the fitted curves of the asymmetry parameter for differentφvalues.The relationship between the harmonic shift and the asymmetry coefficient is expressed awhereqis the harmonic order.This equation enables us to determine the range of harmonic energy shifts given the asymmetry coefficient of the pulse.In this context,Kis found to be 5.5.The fitted curves for the asymmetry coefficients are provided for Fig.3(c).It is evident that the trend of harmonic intensity variation withφaligns with the asymmetry coefficient trend.Furthermore, Fig.3(c)also showcases the appearance of semi-integer order harmonics in the harmonic spectrum.The frequency shift of these semi-integer order harmonics is significantly pronounced asφchanges.
Continuing our analysis, we delve into the reason behind the emergence of semi-integer order harmonics.The time evolution of the laser electric field under sinusoidal bit-phase modulation atφ=0(red solid line)andφ=π(blue solid line)is illustrated in Fig.4(a).The field predominantly governing the emission of higher harmonics corresponds to a time range from-8 o.c.to 8 o.c., depicted by the green background region.Further insight is gained from the time-frequency analysis schematic for the interval from-8 o.c.to 8 o.c.atφ=0,as shown in Fig.4(b).This analysis unveils three harmonic emissions within each cycle,situated at-4 o.c.to-4 o.c.the first emission occurs in the initial half of each cycle,while the second half of the cycle witnesses two harmonic emissions with a relatively shorter time interval and comparable emission intensity.To investigate the unique harmonic emission pattern,a classical trajectory analysis is undertaken and presented in Fig.4(c).This figure provides an enlarged view of the region corresponding to Fig.4(b)(the enlarged section is enclosed by a navy-blue box in Fig.4(b)).The blue line represents the classical trajectory of the primary return core, and the black line corresponds to the classical trajectory of the secondary return core.Form Fig.4(c),it is evident that the first and second harmonic emissions within each cycle at-4 o.c.to-4 o.c.stem from the primary recombination of electrons.Conversely,the third harmonic emission arises from the secondary recombination of electrons.This analysis offers valuable insights into the origins of these different harmonic emissions within the cycle.
To gain deeper insights into the origin of semi-integer order harmonics, we aim to untangle the contribution of the third harmonic emission.This is achieved by reducing the influence of the secondary back-core electrons on higher order harmonics, accomplished by decreasing the strength of the electric field.In Fig.5(a), we present the schematic of the time-frequency analysis of time 0 o.c.-4 o.c.at an electric field strength of 0.04, with other parameters maintained as the same as those in Fig.4(c).Here, it becomes evident that the contribution of secondary recombination electrons to higher order harmonics is significantly suppressed, with no discernible contribution to harmonics beyond the 110th order.Simultaneously, the two primary recombination electrons no longer contribute equally to various harmonics.Figures 5(b)-5(d)display the variation of harmonic intensities for different orders withφat the electric field strength of 0.04.Specifically, Fig.5(b) examines the 135th to 140th order harmonic intensities,showcasing only one contribution from the second harmonic emission of the nucleus return electron.In this case,only integer-order harmonics are observed in the spectrum.In Fig.5(c), we analyze the 100th to 105th order harmonic intensities.Here,there are two harmonic emissions corresponding to nucleus return electrons.We observe that the harmonic spectrum exhibits not only integer-order harmonics but also non-integer-order harmonics between the two emission components.This results from the interference between the two primary nucleation electron emissions.Figure 5(d)delves into the harmonic intensities of the 45th to 50th orders.With the inclusion of harmonic emissions from secondary nucleation electrons, the harmonic interference becomes more intricate,leading to the presence of numerous non-integer-order harmonics.These findings reinforce our conjecture, which departs from the traditional generation of half-integer order harmonics via two-color fields.The emergence of semi-integer order harmonics within a monochromatic linearly polarized field can be attributed to the interference between multiple nucleation-back electron harmonics.This discovery opens up a novel avenue for generating semi-integer order harmonics.

Fig.4.(a) Time evolution of the laser electric field after shaping of sinusoidal phase-modulated pulses for φ =0 (red solid line) and φ =π (blue solid line).(b)Schematic of the time-frequency analysis of time-8 o.c.to 8 o.c.(c)An enlarged version of(b)(in which the blue line is the classical trajectory for the primary return core,and the black line corresponds to the classical trajectory for the secondary return core).

Fig.5.The field strength is 0.04 a.u.,the other parameters are the same as those in Fig.4(c).(a)The time-frequency analysis schematic for 0 o.c.-4 o.c.(b)-(d)The variation of harmonic intensities of different orders with φ.
In order to further understand the role of the inhomogeneous field, the corresponding time-frequency analysis schematic of time 0 o.c.-4 o.c.is given in Fig.6(a) atφ=0(in which the blue line is the classical trajectory for the primary return core,and the black line corresponds to the classical trajectory for the secondary return core).Comparing with Fig.4(d),we observe that the addition of the inhomogeneous field greatly modulates the electron motion, resulting in two high-intensity harmonic emissions in the second half of each cycle of the time-frequency analysis.It is also further verified that the semi-integer harmonics appear due to the interference of the harmonics of the primary and secondary return cores,which does not occur in the case of the homogeneous field.Figures 6(b)-6(d)display the variation of harmonic intensities for different orders withφin the case of the homogeneous field ofE0=0.18, in which all other parameters are the same as those in Fig.3(d).Referring to Fig.3(d),we find that in contrast to the homogeneous field, the inclusion of the inhomogeneous field gives us a continuously tunable harmonic spectrum.It can be found that the secondary return core electrons only act on the lower order harmonics, whereas the continuously tuned harmonic spectrum is not obtained even if only the primary return core electrons act at 85-95 orders.
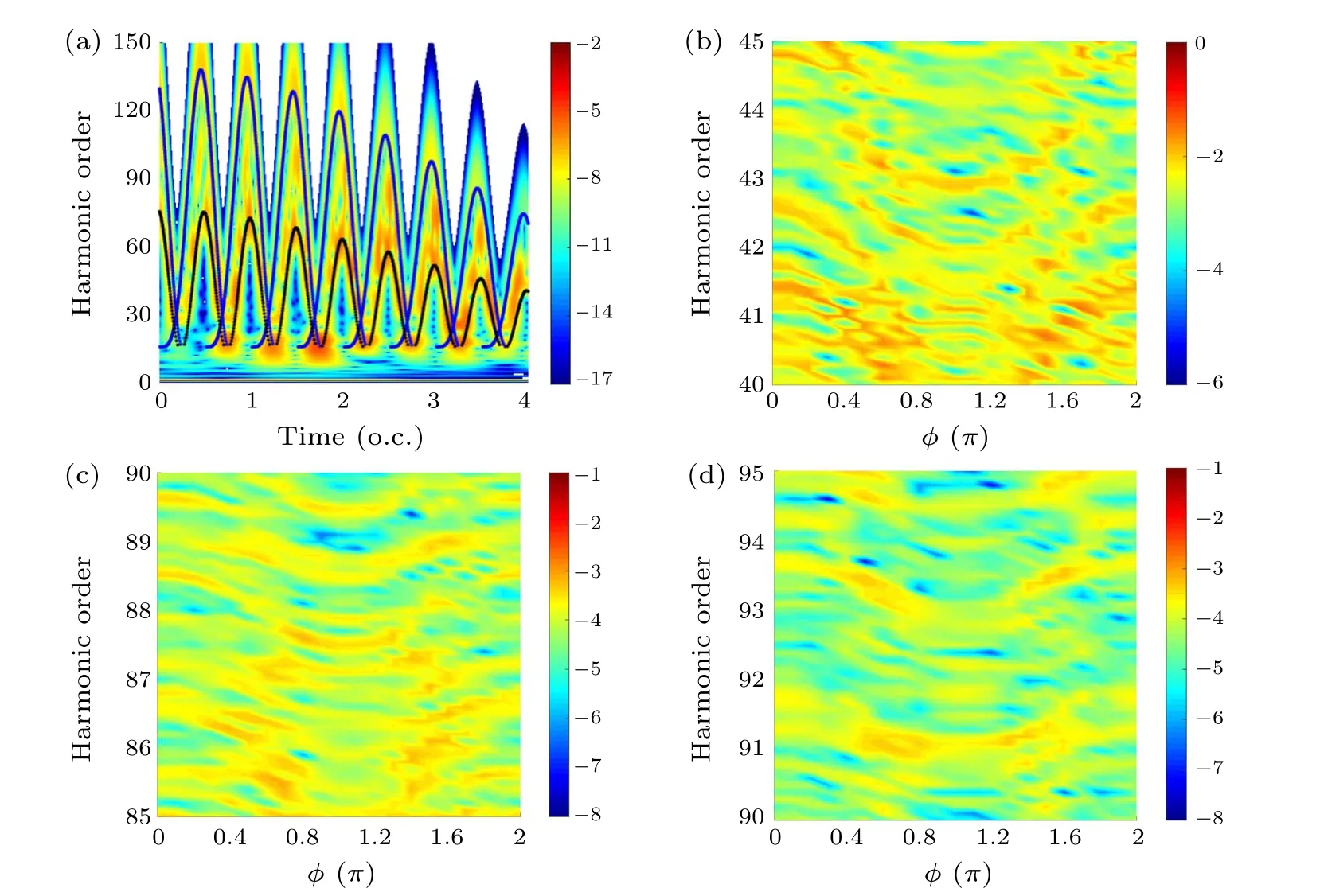
Fig.6.The field strength is 0.18 a.u.in the case of the homogeneous field,for the other parameters as the same as those in Fig.3(c).(a)The time-frequency analysis schematic for 0 o.c.-4 o.c.(b)-(d)The variation of harmonic intensities of different orders with φ.
4.Conclusions
In summary, through theoretical solutions of the timedependent Schr¨odinger equation, we have conducted a thorough investigation into the modulation of harmonic spectra through the manipulation of the absolute phase of a plasmonassisted sinusoidal phase-modulated shaping pulse.Our findings reveal two key aspects of the harmonic emission process.Firstly, we observed that the harmonic spectrum is subject to significant frequency shifts as the absolute phase is altered.These shifts encompass both continuous red and blue shifts of harmonic peaks.This modulation in frequency results from the asymmetry in the envelope of the driving laser pulse,which is responsible for the spectral changes.Secondly, our analysis identified the emergence of semi-integer order harmonics within the harmonic spectrum.This occurrence is attributed to the intricate interference patterns of harmonics resulting from multiple electron emissions and nucleation events.The appearance of semi-integer orders offers a novel avenue for generating these specific harmonics and enhances the overall degree of harmonic tune-ability.
Our work not only presents a novel approach for obtaining semi-integer order harmonics but also extends the range of possibilities for continuous harmonic modulation, thus advancing the field of high-order harmonic generation.
Acknowledgments
This project was supported by the National Key Research and Development Program of China (Grant Nos.2022YFE134200 and 2019YFA0307700), the National Natural Science Foundation of China (Grant Nos.11604119,12104177,11904192,12074145,and 11704147),and the Fundamental Research Funds for the Central Universities (Grant Nos.GK202207012 and QCYRCXM-2022-241).
——中华第一玉龙
- Chinese Physics B的其它文章
- Does the Hartman effect exist in triangular barriers
- Quantum geometric tensor and the topological characterization of the extended Su–Schrieffer–Heeger model
- A lightweight symmetric image encryption cryptosystem in wavelet domain based on an improved sine map
- Effects of drive imbalance on the particle emission from a Bose–Einstein condensate in a one-dimensional lattice
- A new quantum key distribution resource allocation and routing optimization scheme
- Coexistence behavior of asymmetric attractors in hyperbolic-type memristive Hopfield neural network and its application in image encryption

