Versatile and controlled quantum teleportation network
Yao-Yao Zhou(周瑶瑶), Peng-Xian Mei(梅鹏娴), Yan-Hong Liu(刘艳红), Liang Wu(吴量),Yan-Xiang Li(李雁翔), Zhi-Hui Yan(闫智辉), and Xiao-Jun Jia(贾晓军)
1Department of Physics,Taiyuan Normal University,Jinzhong 030619,China
2College of Information Engineering,Shanxi Vocational University of Engineering Science and Technology,Jinzhong 030619,China
3Shanxi North Machinery Manufacturing Co.,Ltd,Taiyuan 030000,China
4State Key Laboratory of Quantum Optics and Quantum Optics Devices,Institute of Opto-Electronics,Shanxi University,Taiyuan 030006,China
5Collaborative Innovation Center of Extreme Optics,Shanxi University,Taiyuan 030006,China
Keywords: quantum teleportation,coherent feedback control,versatile,controlled transformation
1.Introduction
Quantum teleportation,[1-8]one of the most basic quantum protocols, transfers an unknown quantum state from one location to another through local operation and classical communication via shared quantum entanglement without physical transfer of the information carrier.It has been widely applied in various quantum information protocols,such as entanglement swapping,[9]quantum repeaters,[10]quantum gate teleportation,[11]quantum computation based on measurement,[12]and quantum teleportation networks,[13]which have high application value in quantum computation and quantum information.[14-16]The concept of quantum teleportation was first proposed by Bennettet al.in 1993 in the discrete variable (DV) domain.[1]In 1994, Vaidman proposed a quantum teleportation scheme in continuous variables(CVs),in which entangled optical fields,joint measurements,and information transformations were used to realize the transfer of an unknown quantum state.[17]Later, many theoretical and experimental investigations of DV and CV quantum teleportation were carried out.[18-22]
With the further development of quantum information research, it is necessary to transfer quantum states or quantum information among increasing numbers of users.Multipartite quantum protocols are expected to form fundamental components for larger-scale quantum communication and computation,[23-25]such as quantum key distribution (QKD)networks,which are promising to serve large numbers of users with information-theoretic secure communication.[26]Thus a quantum teleportation network involving multiple users is essential for future quantum internet.[13,27]A quantum teleportation network is a quantum communication network based on multipartite entanglement, in which multiple users are spatially separated and over which they have previously shared multipartite entanglement.Any pair of users can choose to transfer an unknown quantum state among specific users in the quantum network, which provides a foundation to construct the complex and diverse quantum communication and quantum computation.[28,29]The open-destination teleportation with five-photon entanglement has been realized.[28]The schemes of quantum teleportation using multipartite entanglement have been demonstrated, and the sent quantum state can be conditionally recovered and reconstructed at any of the multiple receivers.[30,31]Besides,the generation and detection of CV entanglement sources are efficient.The CV quantum network enables to construct metropolitan quantum networks with multiple users,[32,33]and thus it is possible to implement controlled teleportation of any unknown quantum state.The controlled quantum teleportation is demanded in practical applications.Sometimes it is required to teleport the quantum state within fewer users instead of all the users,and the whole quantum resource of multipartite entangled state can be divided into several sub-networks to simultaneously implement versatile quantum communications.
Here, based on a CV six-partite Greenberger-Horne-Zeilinger (GHZ) entangled state, we propose a highly versatile and controlled teleportation network with six users.First,six spatially separated users are connected in a network over which they have previously shared six-partite entanglement.Then,an unknown quantum state is jointly measured together with one mode of the GHZ entangled state in the input node,and the measurement results are transmitted selectively to any one of the remaining five nodes through different classical channels according to actual demand.Because of the quantum correlation among six users,to complete the reconstruction of the unknown quantum state, the sender and receiver may require assistance from multiple controllers.The number of controllers has a strong influence on the effect of the teleportation,so the flexibility to change the number of controllers required in a quantum network is meaningful.To control the minimum number of controllers required for successful quantum teleportation,three nondegenerate optical parametric amplifiers with coherent feedback control(CFC-NOPAs)are used to generate the six-partite GHZ entanglement.[34]The dependence of the teleportation fidelity on the transmissivity of the control beam splitter(CBS)is theoretically analyzed.Our scheme includes two operations.One is for the entanglement source.The entanglement degree of the entanglement source is adjusted by adjusting the transmittanceTof the control coupling mirror in the CFC system.Different entanglement degree leads to different quantum teleportation networks that can be constructed;the other operation is for users in the network, who can control where their information goes and communicate flexibly as sub-networks.These two operations are independent of each other.
In multiple user networks, quantum states can be transferred between different sub-networks consisting of different senders, receivers and controllers.More users, such as six users,can perform different kinds of subnetworks,to demonstrate the versatility.Versatility means that quantum teleportation can be implemented among various combinations of different users.In the CV GHZ state not only there are quantum correlations among all the users; but also there still exist quantum correlations with some users with proper squeezing factor.With such a CV GHZ state, quantum users can selectively transmit their information to other users in different subnetworks, which construct a versatile teleportation network.It can demonstrate two three-user subnetworks for controlled quantum teleportation, and three two-user subnetworks for quantum teleportation,which satisfy different applications with different user combinations.Moreover, the versatile quantum teleportation network can be flexibly realized only by controlling the CFC system, where the critical experimental conditions and any change of the hardware are not needed.We use a single continuous-variable six-partite(GHZ)state to realize such a task by choosing the different measurement and feedback operations.The controlled teleportation network, which includes one sub-network, two sub-networks and three sub-networks, can be realized for different application of user combinations.Our approach is flexible and scalable,and is expected to be a versatile platform to demonstrate the complex quantum communication and quantum computing protocols.
2.Controlled quantum teleportation network
Complex quantum teleportation networks,which include a quantum server and multiple quantum users,are fundamental elements of protocols such as large-scale quantum communication networks and distributed quantum computation.Figure 1 shows the schematic diagram of a multiuser controlled quantum network, in which users are distributed at different locations in space.With the support of quantum server,some applicable users can be selected to cooperate with each other to form subnetworks.By controlling the characteristics of the quantum server, the characteristics of the subnetwork can be controlled, such that controllable transformations among different types of subnetworks can be realized.Multipartite entangled optical field is the basis of realizing quantum teleportation network.A general way to build CV multipartite entangled states in experiments is to achieve a linearly optical transformation of input squeezed states on a specific beam-splitter network.[35]If ˆalandUklrepresent the input squeezed state and unitary matrix of a given beam-splitter network, respectively,the output optical modes after transformation are given by ˆbk=∑l Uklˆal,where the subscriptslandkexpress the designated input and output modes,respectively.A CVN-partite GHZ entanglement state can be generated usingnsqueezed states and a network with multiple beam splitters,and the CV GHZ quadrature correlations can be expressed as[27]



Fig.1.Schematic diagram of a multiuser quantum teleportation network.
Figure 2 is the specific structure of the quantum server,in which an off-line CFC-NOPA can simultaneously generate an ˆx-squeezed state and a ˆp-squeezed state,[34,36]and each of the five beam splitters has a corresponding beam-splitting ratio.The three ˆx-squeezed states ˆa1, ˆa3, ˆa5, and three ˆp-squeezed states ˆa2, ˆa4, ˆa6generated by three CFC-NOPAs are expressed as ˆam= e-rˆx(0)m+i erˆp(0)m(m= 1,3,5), and ˆan= erˆx(0)n+i e-rˆp(0)n(n=2,4,6),respectively.In this case,ris a squeezing factor and ˆx(0)and ˆp(0)represent the quadrature-amplitude and the quadrature-phase operators of the corresponding vacuum field with noise varianceV(ˆx(0))=V(ˆp(0))=1/4.
We have assumed that all squeezed states produced by the three CFC-NOPAs have equal squeezing degrees owing to their identical configurations.According to the preparation method shown in Fig.2,the transformation matrix can be decomposed into

According to the transformation matrixU6, the relationship between the output and input optical fields can be expressed as follows:
Then the quantum correlation variances of the quadrature amplitude-sum and relative quadrature phase-difference can be determined by
At the limit of infinite squeezing, namelyr →∞, all of these quantum correlation variances approach zero and the CV GHZ state is a maximally entangled state.According to the inseparability criteria for CV multipartite entangled states proposed by van Loock and Furusawa,[37]we can deduce the inseparability criteria for the CV six-partite GHZ state as follows:
whereg(i)(i=1,2,3,4,5) is the gain factor.For the case of ideal squeezing,g(i)=1, whereas for the case of non-ideal squeezing,the gain factorg(i)can be adjusted to minimize the value on the left-hand sides of the inequalities which are called optimal gain factors.When all variance combinations on the left-hand sides are less than 1,the six output optical modes are in a six-partite GHZ state.
It should be stressed that CFC-NOPAs are used for the preparation of a six-partite CV GHZ entanglement state instead of NOPAs.The schematic diagram of NOPA with coherent feedback control is shown in the insert of Fig.2.The CFC loop is composed mainly of mirrors coated with highreflection for seed beams and a CBS.The effect of CBS makes the input optical fields of the NOPA and the final output optical fields of the CFC-NOPA system consist of two parts: part of the coherent state and part of the output entangled state from the NOPA.Theoretical analysis and experimental verification of the CFC-NOPA system have been described in detail in Ref.[34].By tuning the transmissivity of the CBS in the CFC,the squeezing factors of the output optical entangled state of the system can be improved or reduced.Thus,the entanglement degree of the six-partite entanglement source used in quantum teleportation can be freely regulated, which is of great significance in building a flexible and controllable quantum teleportation network.
3.Performance of controlled quantum teleportation networks
Both coherent states and nonclassical states, such as squeezed states and entangled states can be teleported by using quantum entanglement resource.[38]Here,we take the teleportation of a coherent state as an example for theoretical analysis.Before the teleportation of a coherent state, submodes(ˆb1,ˆb2,...,ˆb6) of the six-partite GHZ entanglement are distributed in advance to the six spatially separated users(which we call user 1, user 2,..., and user 6), and these six users can play any role among sender,receiver and controller during quantum teleportation.The controller refers to the users other than the sender and receiver involved in the quantum teleportation process, which can control the success and failure of a quantum state transfer from the sender to the receiver by restricting the sender and receiver’s access to their information.
Figure 3 shows a highly versatile and controlled quantum teleportation network with the ability to switch among various combinations of different users.In general, the transmission process of quantum states is described below.If the combination of sender user 1, receiver user 2, and other users of the controller is selected to perform the teleportation of a coherent state.First, sender user 1 couples her entangled mode(ˆb1)and an unknown input mode(ˆain)on a 50%beam splitter and performs measurements on two outputs of the half beam splitter with two optical homodyne detectors.Two outputs of the half beam splitter are labelled asandfor relevant quadratures.The measurement results from two optical homodyne detectors for ˆxuand ˆpνare fed forward to receiver user 2 through classical feedforward circuits with gain factorsgxandgp, respectively, where we have assumed that the two classical channels of user 1 have the same normalized gainsgx ≈gp ≈1 and that any phase offsets have been appropriately compensated.[8,13]The other users (four controllers) measurexquadratures of their entangled modes ˆxb j(j=3,4,5,6)and the measurement results are fed forward to receiver user 2 through classical feedforward circuits with gaingj(j=3,4,5,6).User 2 uses the received measurement results to modulate an independent laser by applying electro-optical modulations (EOMs) including amplitude and phase modulations.The amplitude and phase modulations correspond to the displacement ofxandpquadratures,respectively.The modulated beam is combined with the receiver’s mode ˆxb2and ˆpb2at a 1/99 beam splitter.One output of this beam splitter is the receiver’s reconstructed output state.The 1/99 splitting is used to implement feedforward operation.The measurement results of balanced homodyne detectors(BHDs)are fed forward to the EOMs,which can be directly placed in the optical beam of receiver and the loss due to EOM is unavoidable.Alternatively,the EOMs are placed in an auxiliary laser, and the transmitted modulated signal through 1/99 splitting is coupled with the optical beam of receiver.In this way, the loss of EOM can be ignored.The receiver uses the received measurement results to displace his optical beam.The displaced quadrature amplitude and phase are defined according to BHD measurement results and gain factor, which can optimize teleportation fidelity.
The mode reconstructed by user 2 becomes
In the ideal case, if the gains are taken asg3=g4=g5=g6= 1, the total position and relative momentum satisfy ˆxb1+ˆxb2+ˆxb3+ˆxb4+ˆxb5+ˆxb6→0 and ˆpb1- ˆpb2→0,respectively.At this point,the teleported state is identical to the input state.In the case of finite squeezing,the teleported state is not exactly the same as the input state,so it is necessary to study the overlap between them.To evaluate the overlap between the teleported state and the input state, i.e., the performance of teleportation,we use fidelity defined asF=〈Ψin|ρout|Ψin〉,
whereΨinis the input state andρoutis the density matrix of the output state.[39,40]With a finite degree of squeezing, the fidelity for quantum teleportation of a coherent state can be written as
whereδx=V(ˆxtel)andδp=V(ˆptel).[27]
Taking Eqs.(3) and (6) into Eq.(7), it can be seen that the degree of squeezing and the controller’s gain factors affect the teleportation fidelity strongly.It is worth mentioning that the value of the gain factor can be zero.If the gain factors of some controllers are 0, it means the number of controllers in the subnetwork changes.Depending on the number of controllers,subnetworks with different combinations of users can be constructed, resulting in different quantum teleportation performances, as shown in Figs.3(a)-3(c).Figure 3(a) corresponds to the combination where the sender is user 1, the receiver is user 2,and other users are controllers.Figure 3(b)is the schematic of a quantum teleportation network including three subnetworks.In this scheme, any combination of one sender and one receiver constitutes a complete teleportation system and the teleportation of three quantum states can be performed simultaneously with equal fidelity.Figure 3(c)is the schematic of a quantum teleportation network including two subnetworks.As shown in Fig.3(c),user 3 measuresxquadrature of her entangled mode and the measurement result is fed forward to receiver user 2 or receiver user 6.In the case where the measurement result is fed forward to receiver user 2,any combination of one sender,one receiver and one controller constitutes a complete teleportation system and the teleportation of two quantum states can be performed simultaneously with equal fidelity.For the other case where the measurement result is fed forward to receiver user 6,any combination of one sender and one receiver constitutes one complete teleportation system and the remaining four users acting as a sender,a receiver and two controllers constitute the other complete teleportation system.In this case, the teleportation of two quantum states can be performed simultaneously but with different fidelities.Because of the different numbers of controllers in these three schemes,the performances of quantum teleportation presented in each differs,including the number of quantum states that can be transmitted and the fidelity of teleportation.Thus, whether a sender and a receiver need the information from the other controllers and how many controllers they need is an important consideration for the successful implementation of a quantum teleportation.

Fig.3.Schematic of a highly versatile and controlled quantum teleportation network.ˆain: coherent state output from the laser to be transmitted;ˆaout: reconstructed output state; ˆxu: amplitude component of the Bell measurement; ˆpν: phase component of the Bell measurement; EOM:electro-optical modulations;HD:homodyne detector.Detailed description is shown in Table 1.

Table 1.Detailed description of Fig.3.

CBSs in CFC systems play an important role in achieving flexible control of the number of controllers.By combining the relationship between squeezing factors and the transmissivityTof the CBS in a CFC-NOPA system,we theoretically calculate the dependences ofF2,F3,F4,F5, andF6on the transmissivityTof the CBS according to the five situations above.For the calculation, the experimental parameters are selected as follows: the transmissivity of the output coupler of the NOPA is 0.05,the nonlinear conversion efficiency is 0.01,the total extra loss in the CFC loop is 0.02 and the analysis frequency of the spectrum analyzer is 2 MHz.The calculation results are shown in Fig.4.Figures 4(a)-4(c) correspond to the fidelity of quantum teleportation in the experimental setup shown in Figs.3(a)-3(c).In Fig.4,trace 1 shows the classical limit of teleportation.Traces 2,3,4,5,6 correspond to dependences ofF2,F3,F4,F5,andF6on the transmissivityTof CBS.In Fig.4(a),the fidelity shown in trace 6 is always greater than the classical limit value whenTchanges from 0 to 1.This is because regardless ofTchanges, the six submodes used for teleportation are always entangled.In Ref.[38], the teleportation fidelity of a coherent state by using entangled states is greater than the classical limit 1/2.WhenT=0, the entire output optical field from NOPA is reflected, the final output light from CFC-NOPA is a coherent state, and the teleportation fidelity is equal to the classical limit.WhenT=1, the entire output optical field from NOPA is transmitted, and it becomes the final output light of CFC-NOPA.This is equivalent to the case in which the CFC loop does not control the operation of NOPA, namely NOPA operates alone.At this time, the teleportation fidelity is 0.69.When 0.59<T <1,the positive effect of the CFC loop is greater than its negative effect,which makes the entangled degree of the output optical field from NOPA to be enhanced, and so is the teleportation fidelity.AtT=0.87, as the positive effect of the CFC loop reaches its maximum, the fidelity also reaches its maximum.Traces 2, 3, 4 and 5 have the same tendency to first increase,then decrease and increase again whenTvaries from 0 to 1.Similar to trace 6,these four traces also show that the fidelities are the classical limit at transmittivityTequals zero, NOPA operates alone whenTequals 1,and the positive effect of the CFC loop is the maximum whenTequals 0.87, but the difference is that the teleportation fidelity is the minimum whenTequals 0.87.Most importantly,the teleportation fidelities of these four traces are not always greater than the classical limit.Next, we take trace 2 as an example to explain in detail.In Fig.4(b), trace 2 represents the teleportation from the sender to the receiver without any information from all controllers.When 0<T <0.44, the fidelity shown by trace 2 is greater than the classical limit.This is because the negative effect of the CFC loop is stronger whenTis within this range, which weakens the entangled degree of the output optical fields from NOPA and makes the squeezing factors of input states ˆa1, ˆa2,ˆa3, ˆa4, ˆa5, ˆa6smaller.When we use six weakly squeezed states to prepare the six-partite GHZ entanglement, the remaining submodes ˆb1and ˆb2are still entangled after discarding submodes ˆb3, ˆb4, ˆb5, and ˆb6.Then the teleportation from sender user 1 to receiver user 2 without controllers is equivalent to a bipartite quantum teleportation, and the teleportation fidelity by using two entangled submodes ˆb1and ˆb2is greater than 1/2.In contrast, if six highly squeezed states(corresponding to the range of 0.44<T ≤1 in trace 2) are used to prepare the GHZ entanglement, the remaining submodes ˆb1and ˆb2are completely unentangled after discarding all the other submodes and the teleportation from sender user 1 to receiver user 2 without controllers fails.So whenTincreases from 0.44,the fidelity of quantum teleportation gradually decreases from 0.5.UntilTincreases to 0.87, the positive effect of the CFC loop reaches the maximum,but the teleportation fidelity reaches the minimum.IfTcontinues to increase from 0.87, fidelity also increases gradually from the minimum.In the process ofTincreasing from 0 to 1,if the fidelity is less than 0.5,the information of controllers is needed by the sender and receiver in order to achieve teleportation successfully,which corresponds to the situation shown in other traces.
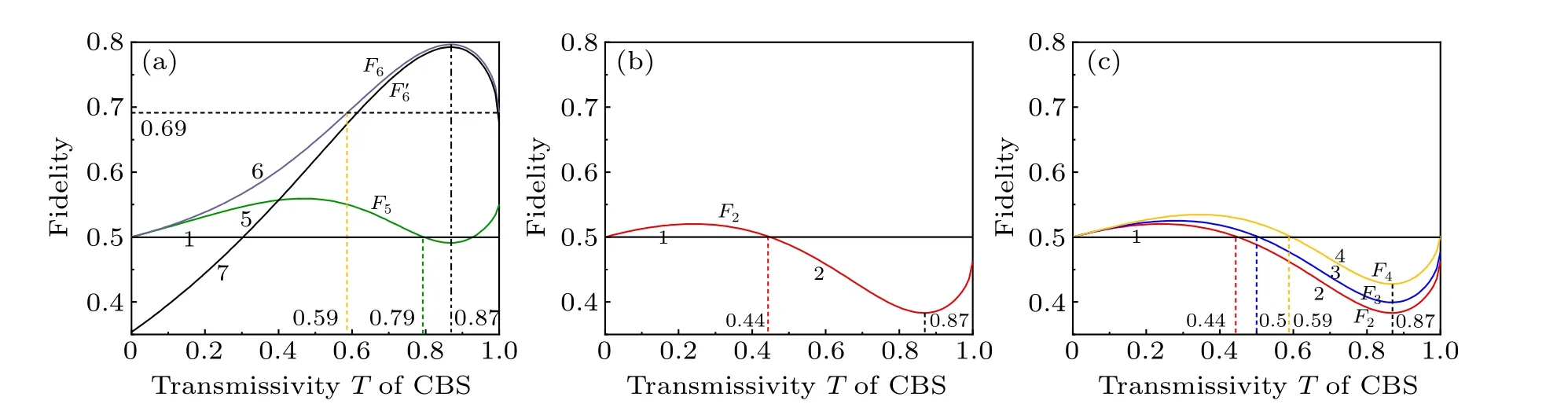
Fig.4.Dependences of the fidelities of F1, F2, F3, F4, F5, F6, and F′6 on the transmissivity T of CBS.(a) One quantum state is teleported with different fidelities.(b)Three quantum states are teleported with equal fidelities.(c)Two quantum states are teleported.Trace 1 shows the classical limit of teleportation.Traces 2,3,4,5,6,and 7 correspond to the teleportation fidelities of F2,F3,F4,F5,F6 and F′6 versus transmissivity T of CBS.
Next,a contrastive analysis on these five traces is helpful to further research on the relationship between the teleportation fidelity and the number of controllers.The corresponding number of user participation in one subnetwork, two subnetworks and three subnetworks are 6, 3 (or the combination of 2 and 4),and 2,respectively.It can be seen from the graph in Fig.4 that 0<T <0.44,0.44<T <0.50,0.50<T <0.59,0.59<T <0.79, and 0.79<T ≤1 respectively correspond to the situations where the minimum number of participants in the quantum network is 2,3,4,5,and 6.Take the example that the minimum number of participants is 3 for detailed analysis.In this case, the sender and the receiver need to get the information from at least one controller to realize the teleportation successfully.Thus the configuration in Fig.3(b)fails to achieve quantum teleportation and quantum teleportation process with only two users in Fig.3(c)also fails.The functions of versatile quantum teleportation network can be clearly represented by Table 2.final fidelity of teleportation is also influenced by other physical parameters.In the above analysis of Fig.4,the gain factors are all optimal values.F6stands for the fidelity with the opti-

Table 2.The functions of versatile quantum teleportation network.
Based on the above analysis, the CBSs in CFC-NOPAs play very important roles in quantum teleportation.On the one hand,according to actual application demand,we can choose any one of these quantum networks to perform teleportation by tuning the transmissivity of the CBS.On the other hand,the final teleportation fidelity can be improved by tuning the transmissivity of the CBS.In addition to transmissivity of CBS,the mal gain factor value ofFor comparison,F′6represents the fidelities with the unity gain factors are shown in trace 7.The value shown in trace 7 is always less than that in trace 6, indicating the importance of the optimal value of the gain factor.Generally,to improve the performance of quantum teleportation,the optimal gain factors are taken.
In terms of efficiency, the generation and detection of continuous variable entangled optical fields are both highly efficient,and this efficiency does not reduce the ultimate fidelity.In terms of bandwidth,the bandwidth of optical fibers is typically several hundred MHz,while the bandwidth of squeezing optical field is about 10 MHz.The bandwidth of the optical fiber does not affect the transmission of the squeezing optical field.However, the bandwidth of the NOPA cavity and the transmission efficiency of the optical field in a quantum teleportation network affect fidelity seriously.The bandwidth of the optical cavity corresponds to the measurement frequency of the spectrum analyzer.Figure 5 shows the calculated dependences of the fidelities of quantum teleportation with four controllers on analysis frequency.Traces 1,2,3 correspond to the fidelities of quantum teleportation when the transmissivity of CBS is selected as 0.2, 0.5 and 0.8, respectively.The fidelity relies on entanglement degree and decreases with the increasing of the measurement frequency as shown in Fig.5.When the frequency is low (kHz), the laser noise is large.The analysis frequency of the spectrum analyzer is 2 MHz in the experiment, because the laser used in the experiment reaches the quantum noise limit.Thus, the frequency spectrum of the quantum fluctuation of quadrature components can be analyzed at 2 MHz.In the quantum teleportation shown in Fig.3(a),the higher the degree of squeezing is,the higher the final teleportation fidelity is.
Next, the relationship between transmission efficiency and fidelity will be considered.Taking the quantum network shown in Fig.3(a)as an example,considering the transmission efficiency of the optical field (ˆb1,ˆb2,...,ˆb6) asξ, the amplitude and phase components of the quantum state measured by receiver are
where ˆxν1,ˆxν2,...,ˆxν6and ˆpν1, ˆpν2respectively represent the orthogonal amplitude and orthogonal phase components of the vacuum noise introduced due to losses.By combining the above formula with the fidelity formula, the relationship between fidelity and transmission efficiency is shown in Fig.6.Higher transmission efficiency leads to better fidelity.Of course,the lower the transmission efficiency,the lower the fidelity,and even lead to transmission failure.
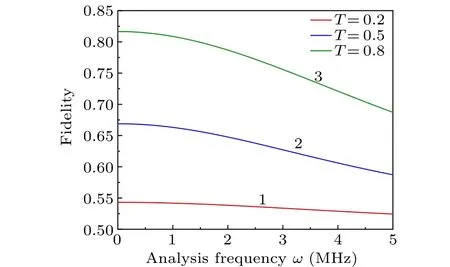
Fig.5.Dependences of the fidelities of quantum teleportation with four controllers on analysis frequency.Traces 1,2,3 are the theoretically calculated fidelities of quantum teleportation when the transmissivity of CBS is selected as 0.2,0.5 and 0.8,respectively.
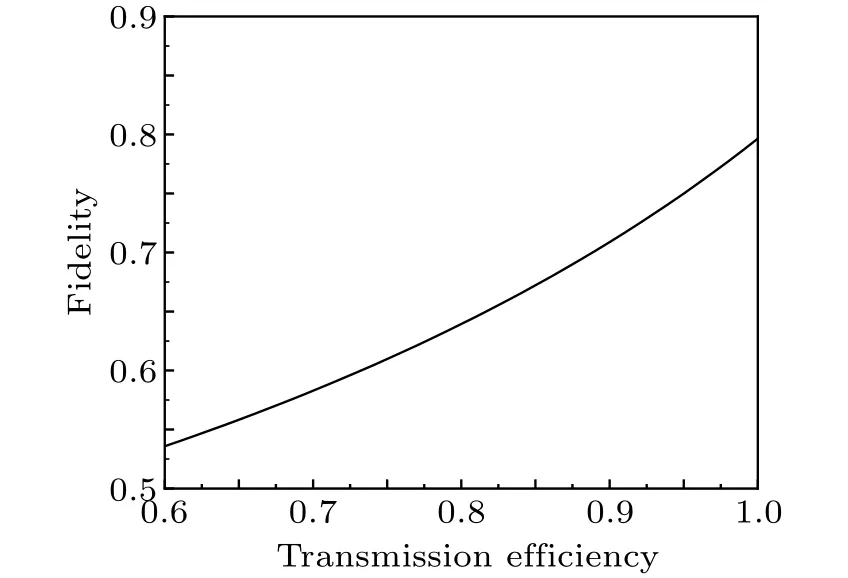
Fig.6.Dependence of the fidelity of quantum teleportation with four controllers on transmission efficiency.
The general procedure of theN-user teleportation network is important, and the six-user is considered as an example to demonstrate the numerical simulation results.TheN-user quantum teleportation network can be realized with anN-partite GHZ entangled state.For a generalN-partite GHZ entangled state,the quadrature amplitude and phase satisfy the relations of
By using the expression of fidelity(Eq.(7)),the quantum teleportation fidelity of theN-user quantum network can be analyzed.
4.Conclusion
We have proposed a highly versatile and controlled teleportation network based on a CV six-partite GHZ entangled state prepared using three CFC-NOPAs.In this scheme,teleportation of a quantum state can occur between any pair of six users according to actual requirements, but may need the assistance of other controllers.By tuning the transmissivity of the CBS in the CFC-NOPA,the minimum number of controllers required in a successful quantum teleportation can be controlled.Depending on the number of controllers, subnetworks with different combinations of users can be constructed.The controlled teleportation network,which includes one,two or three subnetworks has the ability to switch among various combinations of different users.Furthermore, the CFC can manipulate and improve the teleportation performance.We theoretically calculate the dependences of the teleportation fidelities on the transmissivity of the CBS in CFC.The results show that when the transmissivity of CBS is higher, information of more controllers is needed to perform teleportation successfully, whereas when the transmissivity of the CBS is lower, the teleportation can be performed successfully even with information of fewer controllers.The more controllers involved in teleportation,the greater the teleportation fidelity.Due to the large number of users involved in the system, the main challenge is the overall stability.The larger the user number is, the higher the locking requirement is.With the development of locking techniques,[41,42]it is possible to implement a versatile and controllable quantum teleportation network with a larger user number.Our approach is flexible and scalable, and would provide a versatile platform for demonstrations of complex quantum communication and quantum computing protocols.
Acknowledgments
Project supported by the Natural Science Foundation of Shanxi Province of China (Grant No.202203021221214),the National Natural Science Foundation of China (Grant Nos.62122044, 62135008, 61925503, 11904218, 12004276,12147215, and 11834010), the Scientific and Technological Innovation Programs of Higher Education Institutions in Shanxi Province of China (Grant Nos.2019L0092 and 2020L0029), the Key Project of the National Key Research and Development Program of China (Grant No.2022YFA1404500), the Program for the Innovative Talents of Higher Education Institutions of Shanxi Province of China, the Program for the Outstanding Innovative Teams of Higher Learning Institutions of Shanxi and the Fund for Shanxi“1331 Project”Key Subjects Construction.
- Chinese Physics B的其它文章
- Does the Hartman effect exist in triangular barriers
- Quantum geometric tensor and the topological characterization of the extended Su–Schrieffer–Heeger model
- A lightweight symmetric image encryption cryptosystem in wavelet domain based on an improved sine map
- Effects of drive imbalance on the particle emission from a Bose–Einstein condensate in a one-dimensional lattice
- A new quantum key distribution resource allocation and routing optimization scheme
- Coexistence behavior of asymmetric attractors in hyperbolic-type memristive Hopfield neural network and its application in image encryption

