压力作用下高压电缆缓冲层表面电阻特性及等效模型

吴照国，黄会贤，王谦，吴海涛，包健康，李勇，刘佳，徐扬

（1. 国网重庆市电力公司电力科学研究院，重庆 401123；2. 国网重庆市电力公司，重庆 400014；3. 重庆邮电大学，重庆400065）

0 引言

随着城市电网的发展以及土地资源的日趋紧张，高压电缆的应用愈发广泛，其绝缘状态直接关系着整个电力网络的可靠性和稳定性［1-4］。而近年来高压电缆缓冲层烧蚀故障频发，在半导电缓冲阻水层（下文简称缓冲层）上存在烧蚀痕迹并在缺陷处析出白色粉末［5-6］，逐渐劣化电缆主绝缘，最终造成绝缘击穿。缓冲层烧蚀缺陷潜伏性极高，缺陷的发展过程十分漫长，且作用范围大，给城市输电网络的安全运行带来严重的影响［7］。

较多的学者对高压电缆缓冲层烧蚀缺陷的产生机理及发展过程进行了研究［8-15］，以期探索相关的技术手段来保障高压电缆的安全稳定运行。综合现有的研究结果，高压电缆缓冲层烧蚀缺陷是由于受潮的半导电阻水缓冲层带材电阻率变化（受潮的缓冲层导电性降低，化学反应生成的钠盐也具有较低的导电性）导致波纹铝护套与绝缘屏蔽层之间形成不良接触，在波纹铝套波谷与绝缘屏蔽层接触点产生局部电场畸变，逐步劣化高压电缆主绝缘。由此可知，高压电缆缓冲层的电气、机械、散热、阻水等功能要求中［16-18］，导电性能具有举足轻重的作用。

目前对于高压电缆缓冲层导电性的测试主要依据来自JB/T 10259—2014《电缆和光缆用阻水带》［19］。而根据黄宇［20］等人的研究，JB/T 10259—2014标准中电极的接触面积与所采用的压力载荷并不能等效高压电缆缓冲层的实际工作状态，并提出了相应的团体标准T/CAS 374—2019《额定电压26/35kV 以上挤包绝缘电力电缆用半导电缓冲层材料》［21］，对缓冲层体积电阻率以及表面电阻的测试电极进行了改进。

由于高压电缆在电缆隧道中往往采用蛇形敷设方法，导致沿电缆线路长度方向上不同位置缓冲层所受到的机械压力不同，例如电缆支架处的压力与蛇形敷设波谷处的压力。此外，电缆导体与绝缘在重力作用下也会出现一定的偏心状态［22］，导致沿电缆截面一周不同位置处的缓冲层所受压力也不相同。然而现有的研究内容和测试方法中往往忽略了高压电缆缓冲层的导电特性与其实际受到的压力的关系，没有根据电缆实际应力状态建立不同压力下的缓冲层导电特性。本文针对不同压力状态下的高压电缆缓冲层表面电阻特性进行分析，并通过压变电阻网络建立了高压电缆表面电阻测试过程的等效模型。基于本文提出的等效模型可以在按照标准方法获取缓冲层表面电阻以及体积电阻率之后获取不同压力下缓冲层的表面电阻分布范围，用以评估不同压力下的缓冲层的导电性。

1 缓冲层表面导电机理及测试方法

1.1 缓冲层导电机理

高压电缆半导电阻水缓冲层一般由半导电蓬松棉、聚丙烯酸钠阻水粉以及半导电非织布带三层组成［23］。其中，半导电蓬松棉以及半导电非织布带的作用主要是电气连接以及吸收机械膨胀应力，而聚丙烯酸钠阻水粉的作用则是吸水膨胀并阻止水分沿电缆纵向传播。半导电蓬松棉与半导电非织布带的结构类似，均为聚酯纤维中添加纳米炭黑颗粒，如图1所示。

图1 蓬松棉与非织布中炭黑分布示意图Fig.1 Sketch diagram of carbon black distributions in the fluffy cotton and the nonwovens

缓冲层的导电机理主要是通过纳米炭黑填料提供载流子，由炭黑填料之间导电通道以及隧道效应作用实现载流子在聚合物中的迁移。根据导电通道模型，导电粒子的数量越多、间隙越小则材料的整体导电率就越高［24］。而对于未形成导电通道的炭黑粒子的导电机理，一般采用隧道效应进行说明，研究人员提出的用以解释隧道效应的公式均涉及到导电粒子或导电粒子群的间隙，如Ezquerra 等人［25］推导出的材料整体电阻率σ与导电粒子隧道间距的关系如式（1）所示。

式中：d为导电填料的隧道间隙；V为间隙的势垒；m为电子质量；h为普朗克常数。

由上述导电通道与隧道效应的分析可知，缓冲层的导电特性与炭黑填料之间的平均距离相关。而缓冲层中炭黑填料的分布很大程度上由蓬松棉与非织布的聚酯纤维丝结构决定。而蓬松棉与非织布的聚酯纤维结构差异也决定了其导电特性的差异。

1.2 缓冲层表面电阻测试方法

目前可以通过JB/T 10259—2014 以及T/CAS 374—2019 两种标准测量缓冲层表面电阻，如图2所示。两种测试方法最大的区别在于采用的电极尺寸，JB/T 10259—2014 方法规定每个电极的接触面积为200 mm×1 mm，电极间距为200 mm；T/CAS 374—2019 方法为了等效波纹铝护套的节距以及波谷接触面积，规定每个电极的接触面积为30 mm×5 mm，间距为30 mm。此外，两个标准在缓冲层试样尺寸、试验步骤上存在差异，具体如表1所示。

表1 表面电阻测试方法差异Tab. 1 Differences between surface resistance test methods

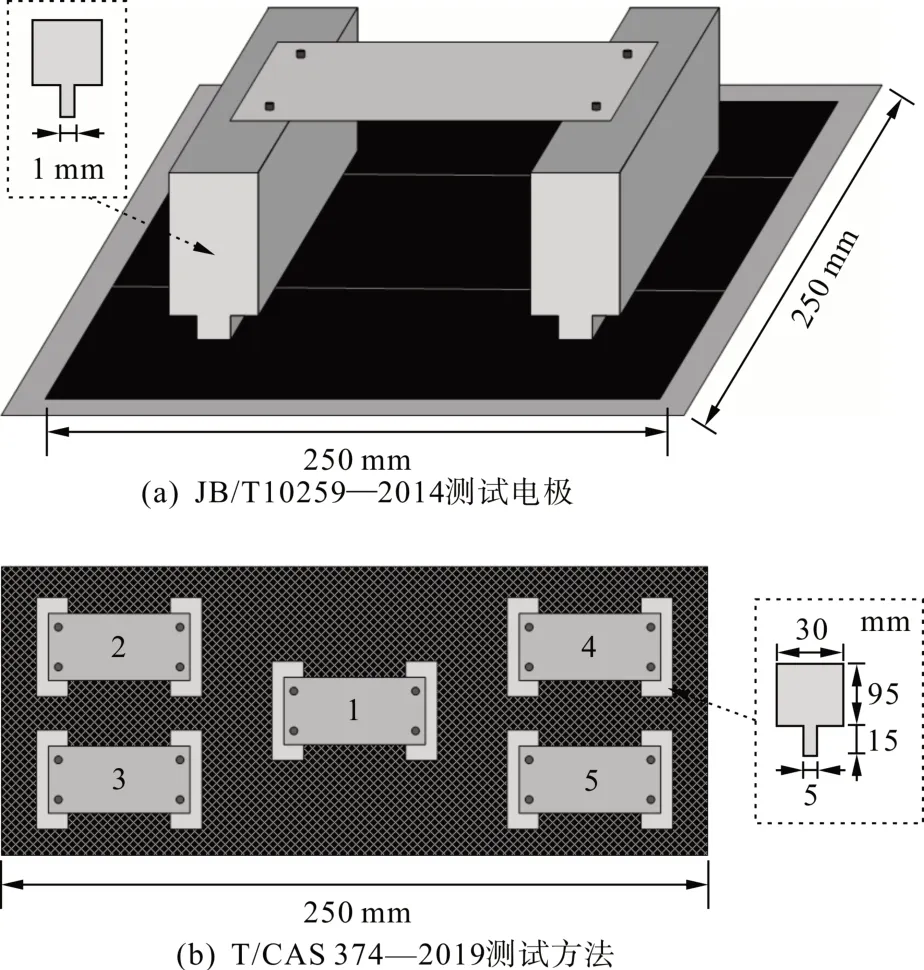
图2 缓冲层表面电阻测试方法Fig. 2 Test methods for surface resistance of buffer layer

值得一提的是，JB/T 10259—2014 中规定了被测缓冲层的尺寸为250 mm×250 mm，对于成品电缆而言无法满足该要求，因此采用3 张80 mm×250 mm 的缓冲层拼接而成一个近似于240 mm×250 mm的试验品，T/CAS 374—2019 中未规定样品的尺寸大小。此外，JB/T 10259—2014 方法中未规定蓬松棉一面向上还是非织布一面向上开展测试，而T/CAS 374—2019方法中规定了蓬松棉一面向上。

1.3 压力作用下表面电阻测试方法

缓冲层是炭黑高聚物复合材料，具有典型的压阻特性，而且缓冲层在实际运行状态下由于敷设落差、弯曲等因素的影响，不同部位受到的压力也不相同，因此本文对压力下的缓冲层表面电阻特性进行了测试，测试方法为在表面电阻测试电极上端的绝缘连接处添加重量递增的砝码，如图3 中上端环氧板处的可调压力。作为对比，在电极之间的缓冲层表面上敷设环氧板，并在环氧板上添加重量逐渐递增的砝码，如图3中下端环氧板处的可调压力。

图3 不同压力作用下缓冲层表面电阻测试方法Fig. 3 Test method of surface resistance of buffer layer under different pressures

2 缓冲层表面电阻测试结果及分析

2.1 缓冲层表面电阻测试结果及特性分析

采用A、B 两个不同厂家生产的高压电缆半导电缓冲阻水带作为试验样品。采用3 张80 mm×250 mm 的缓冲层拼接而成一个近似于240 mm×250 mm的试品按照JB/T 10259—2014 方法进行表面电阻测试，选择其中任一试品采用T/CAS 374—2019 标准选择5 个位置进行表面电阻测试，本文所选位置如图2（b）所示。作为对比测试，两种测试方法下均对缓冲层蓬松棉一侧以及非织布一侧开展表面电阻测试，得到的表面电阻测试结果如图4—5所示。

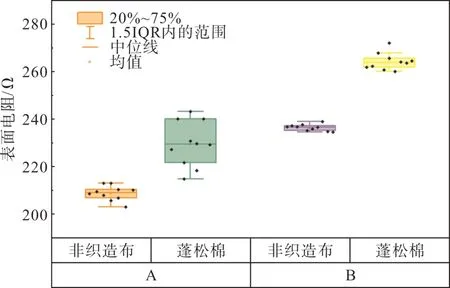
图4 JB/T 10259—2014 表面电阻测试结果Fig. 4 Surface resistance test results according to JB/T 10259—2014

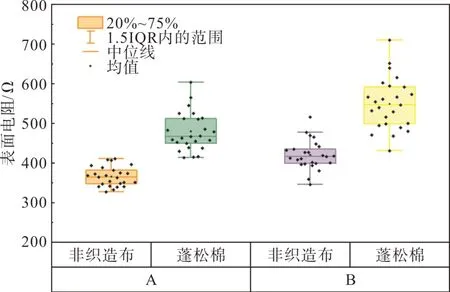
图5 T/CAS 374—2019 表面电阻测试结果Fig. 5 Surface resistance test results according to T/CAS 374—2019

表面电阻测试结果最大值、最小值、平均值以及中位数的具体数据如表2所示。

表2 表面电阻测试结果Tab. 2 Test results of surface resistances

从测试结果可知，缓冲层表面电阻存在较大的分散性，从蓬松棉一面测试的表面电阻的分散性相较于非织布一面的表面电阻分散性更大。此外，无论是A 缓冲层还是B 缓冲层，无论采用哪种标准的方法进行测试，非织布一面的表面电阻均小于该测试情况下的缓冲层一面的表面电阻。

上述结果可由式（1）与图1 进行说明：蓬松棉中聚酯纤维丝的平均间距大于非织布中聚酯纤维丝的平均间距，如图6 中非织布和蓬松棉微观图像所示。

图6 蓬松棉和非织布微观结构Fig. 6 Microstructure of fluffy cotton and nonwovens

对图像进行像素统计，非织布的面密度高于蓬松棉的面密度，聚酯纤维排列更为紧密。炭黑填料主要附着在聚酯纤维上以及团聚在纤维丝的交叉点上，因此可认为蓬松棉中炭黑填料之间的距离d1大于非织布中炭黑填料之间的距离d2，图6 中放大的视域中，标注的炭黑团聚体之间的距离关系也印证了上述观点。又因炭黑填充的聚合物导电性能与炭黑粒子或炭黑团聚体之间的平均距离正相关，因此可以认为非织布一侧的电阻更小，同时，由于蓬松棉中形成导电通道和隧道效应的条件随机性更大，所以蓬松棉一侧所测的表面电阻分散性更大。

由于电极尺寸的差异，依据T/CAS 374—2019标准测试的表面电阻值较依据JB/T 10259—2014 所测试的电阻值大。此外，JB/T 10259—2014 标准中较大的电极尺寸也降低了导电通道的随机性体现，使得采用JB/T 10259—2014 标准测试得到的缓冲层表面电阻值分散性更小。

2.2 压力作用下表面电阻测试结果及特性分析

以JB/T 10259—2014 的测试方法为例开展A、B 两种高压电缆缓冲层在不同压力下的缓冲层表面电阻测试，总计对3 个样片进行测试，对A 缓冲层分别记为A-1、A-2、A-3，对B 缓冲层分别记为B-1、B-2、B-3。压力施加在电极上时，施加砝码的重量以每次1 kg 的增量逐渐增加至10 kg，而压力施加在缓冲层上的时候，受限于空间，最多施加至5 kg。以蓬松棉一侧的表面电阻测试为例，A 和B两种缓冲层表面电阻测试结果如图7所示。

图7 压力作用下缓冲层表面电阻值Fig. 7 Surface resistances of buffer layer under different pressures

根据图7 的测试结果可知，压力施加在电极上时缓冲层表面电阻随着外界压力的增大而明显减小，压力施加在缓冲层表面时表面电阻随着外界压力增加而减小的程度不大。在图1 的基础上结合压力作用下炭黑粒子的平均间距变化规律来说明上述测试结果，如图8所示。

图8 不同压力施加方式对表面电阻测试的影响Fig. 8 Influences of different pressures applying methods on surface resistance tests

当压力施加在缓冲层表面上时缓冲层的聚酯纤维发生位移压缩，而位移的方向基本为沿压力方向，沿电极-缓冲层表面-电极的导电通路上炭黑之间的平均间距几乎没有改变，即图8（a）中所示的载流子迁移路径没有受到压力的影响，表现为表面电阻值基本不随压力的增加而改变。而当压力施加在电极上时，由于电极的接触面积较小缓冲层与电极接触部分的纤维压缩位移较大，因此该部分沿压力方向的炭黑平均距离随着压力的增大而急剧减小，导电性能提升。随着与电极接触区域缓冲层的压缩会形成新的沿缓冲层表面方向的新的导电路径，如图8（b）所示，从而减小两个电极之间的电阻值测试结果。

3 压力作用下缓冲层表面电阻测试电路等效模型

3.1 缓冲层表面电阻等效电路模型

缓冲层表面电阻测试过程的等效电路如图9 所示。根据图8 所示的载流子导电路径，缓冲层与电极接触区域沿压力方向的体积电阻可视作一系列随压力P变化的电阻Rv（P）串联而成，而压变电阻的值随着压力的增大而减小，因此当压力增大时相当于在表面电阻测试电极之间增加了并联的导电通道，使得测试的结果随着压力的增大而减小。将两个电极之间的缓冲层沿纵向和横向建立分布式电阻网络，其中Rhij（i=1，2，…，n+1，j=1，2，…，m-1）为第i层的第j个等效表面电阻，而Rvij（i=1，2，…，n，j=1，2，…，m）为第i层的第j个等效体积电阻，其值受到该处压力的影响。

图9 压力下表面电阻等效电路Fig. 9 Equivalent circuit of surface resistances under pressures

计算压力施加在电极上时相应的简化模型：假设图中电阻网络矩阵的每一列上电阻相等且受压时的变化情况相同，同时电极中间部分未受到压力影响而改变电阻，因此可以将图9 所示的电阻网络简化为如图10 所示的形式，Rv、Rv1（P）、Rv2（P）、Rh分别为未受到电极压力时每层的体积电阻、左右两侧受到电极压力处的每层体积电阻、未受到压力影响每层的表面电阻。

图10 压力下表面电阻测试简化电路图Fig. 10 Simplified equivalent circuit diagram of surface resistance tests under pressures

图10 所示的简化等效电路模型可以看做一个2×n阶的电阻网络模型，用IRv2、I′Rh、IRh、IRv1、IRv分别为流过Rv2、左侧Rh、右侧Rh、Rv1、Rv的电流，通过网络分析法计算第i层网络的电阻过程如式（2）—（4）所示［26］。

第i个回路两个网孔的电压方程为：

同理可以得到第i-1 个回路两个网孔的电压方程，再经过化简整理便可以得到图10 等效电阻网络的差分方程组模型如式（7）所示。

式中A为系数矩阵。A可表示为式（8）。

根据文献［26］中给出的矩阵变化过程以及差分方程求解可得到不同压力情况下的两电极之间的等效电阻，从而得出表面电阻测试时表面电阻与电极上的压力之间的关系。

3.2 缓冲层表面电阻模型计算分析

为了验证本文所提出的等效模型，以B 缓冲层样品为例进行仿真计算分析。采用JB/T 10259—2014 中缓冲层体积电阻率测试方法对7 个样品进行测试，得到的结果如图11所示。

图11 B缓冲层的体积电阻率与压力的关系Fig. 11 Relationship between volume resistances of buffer layer B and the pressures

通过最小二乘算法对所测试的数据进行拟合，目标函数设置为式（9）。

式中：ρ为缓冲层的体积电阻率；P为压力；ρ0、P0、A1以及t1均为待拟合参数。试样1—7 的待拟合参数ρ0、P0、A1以及t1如表3所示。

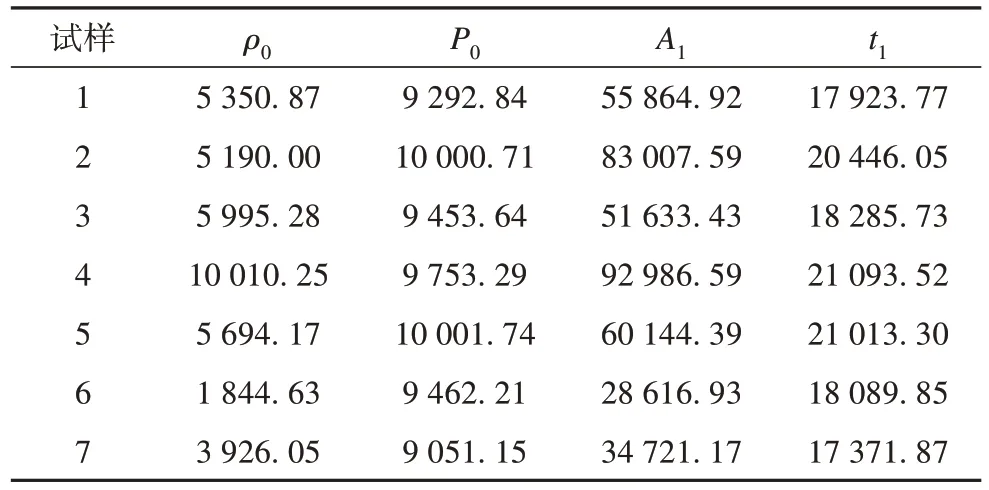
表3 B缓冲层体积电阻率拟合参数Tab. 3 Fitting parameters of volume resistance of buffer layer B

缓冲层带材厚度按照2 mm 计算，根据表面电阻测试电极的几何尺寸可以得到电极接触区域的总体积电阻为ρ/10 Ω，两电极中间区域的总体积电阻为ρ/（2×103）Ω。

缓冲层阻水带中炭黑填料分布具有一定的随机性，因此采用组合的方式对参数进行赋值，即电极与缓冲层接触区域的体积电阻率采用表3 所示的7组数据，而Rh在表面电阻测试过程中不受压力影响而改变，因此采用图4 中蓬松棉的测试结果推导等效模型中的Rh的值，推导过程采用对称型电阻网络进行相关计算，即Rv1=Rv2，该情况下2×n阶的电阻网络模型将退化为n阶梯形网络，如图12所示。

图12 n阶梯形网络及其等效模型Fig. 12 n-order ladder network and its equivalent model

例如采用4 网孔的等效电阻网络结构，即n=2，通过图11 的退化模型以及图2（c）中蓬松棉层的测试数据可得到每组数据下的Rh值，选择所有的Rh值中最大值、最小值作为分析组合数据。同时Rv1与Rv2的值在图11 的7 组测试数据中组合选取，求取不同压力下的缓冲层表面电阻数值，得到的结果如图13 所示，图中仅标明了部分组合的计算曲线，实际上，所有组合的计算结果可以用图中阴影填充区域表示，即该缓冲层测试样品在不同压力下的表面电阻测试值均落在该区域内。

图13 表面电阻二阶模型仿真结果Fig. 13 Simulation results of surface resistances of 2-order model

按照上述计算方式对更高阶数的电阻网络模型进行计算，得到的表面电阻测试范围区域结果如图14 所示。由图14 可知，不同阶数的表面电阻范围存在一定的差异，且随着阶数的增加，区域的涵盖范围更广，但是覆盖范围的增加速度逐渐减小。为了平衡计算精度以及速度，本文提出的表面电阻计算方法可采用4阶模型。

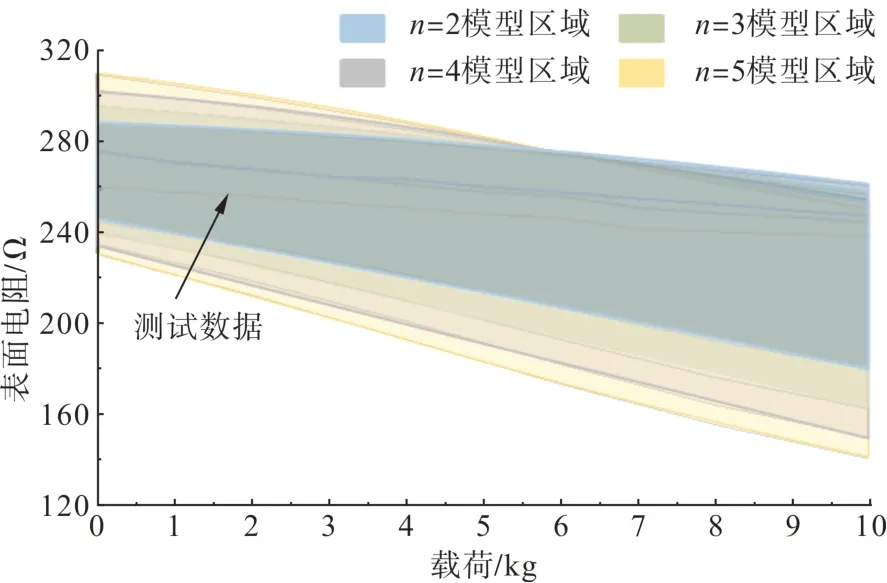
图14 不同阶数模型仿真结果Fig. 14 Simulation results of different model orders

通过本文提出的模型，仅需要按照标准方法获取表面电阻以及体积电阻率的测试结果，便可以得到不同压力下缓冲层的表面电阻分布区域，为高压电缆缓冲层在实际复杂运行工况下的导电特性分析提供有力支撑。

4 结论

本文对两种高压电缆半导电缓冲阻水带进行了表面电阻测试，通过统计结果发现，非织布一面的表面电阻小于该测试情况下的缓冲层一面的表面电阻，蓬松棉一面测试的表面电阻分散性更大。通过在测试电极以及电极之间的缓冲层表面上施加不同重量的载荷，研究了缓冲层表面电阻与施加压力的关系，当压力施加在电极上时表面电阻值随着压力的增大而显著减小；当压力施加在电极之间的缓冲层表面上时表面电阻测试值几乎不随压力的增加而改变。

本文建立了n阶电阻网络模型来表征高压电缆缓冲层表面电阻测试特性：基于最小二乘拟合算法得到体积电阻率与压力的关系，并通过2×n阶电阻网络退化为梯形电路获取分层的表面电阻值，最终以差分方程模型获取高压电缆缓冲层表面电阻在不同压力下的测试值分布范围。通过本文所提出的模型可以在按照标准方法获取缓冲层表面电阻以及体积电阻率之后得到不同压力下缓冲层的表面电阻分布范围，用以评价缓冲层的导电性，为高压电缆实际运行工况提供技术支撑。