基于硬件在环仿真的DFIG 并网系统开环模式谐振风险及验证

陈江，杜文娟，杨佳

（1. 四川大学电气工程学院，成都 610065；2. 南瑞集团有限公司，南京 211106）

0 引言

传统的电力系统振荡主要包含低频振荡和次同步振荡，是威胁电力系统安全稳定运行的重大因素。有关电力系统振荡风险的实验研究由于其安全性和成本高昂等问题难以进行，而Simulink 等离线仿真工具计算速度较慢，不具备与实际装置交互的能力［1］，近年来兴起了名为硬件在环（hardware in the loop，HIL）的数模混合仿真实验［2-3］。HIL 仿真能模拟多种工况，参数便于调试，成本易于控制，且实验环境安全可靠、环保节能。

随着大规模风电并网，电力系统也迎来了更多的振荡风险［4-6］。开环模式谐振理论为解释这类问题提供了新的视角。文献［7］在研究永磁同步发电机（permanent magnet synchronous generator，PMSG）与电力系统间动态交互时，通过阻尼转矩分析引入了开环模式谐振的概念，认为在开环模式谐振条件下PMSG 在系统机电暂态过程中会呈现强惯性，有可能对功角稳定产生负面影响。文献［8］从开环模式谐振的角度研究了风机控制系统中锁相环（phase-locked loop，PLL）和其他环节间的动态交互作用，提出一种预测开环模式谐振条件下相应闭环特征根的方法，用于评估系统阻尼水平。文献［9-11］分别研究了开环模式谐振引起的电力系统低频振荡、含双馈感应发电机（doubly-fed induction generator，DFIG）风电场并网的电力系统次同步振荡（sub-synchronous oscillation，SSO）现象，阐述了开环模式谐振理论在多类型电力系统振荡的稳定性分析中的适用性。文献［12］探讨了次同步控制相互作用问题中负阻机理和开环模式谐振机理之间的联系，两者相互补充。综上所述，开环模式谐振理论研究已较为完善，可以解释大部分电力系统振荡失稳的现象［13］，缺陷在于其实验数据空白，工程应用指导意义尚难明确，且此前的研究均采用平均模型进行，对系统暂态特性分析将会大打折扣［14］，时域仿真结果不够可靠。

本文针对开环模式谐振理论研究的实验空白进行补充，搭建DFIG 并网系统HIL 实验平台，给出详细的控制系统模型，提出了开环模式通用分析方法，从开环模式谐振角度解释了并网DFIG 引起的SSO，进行HIL 实验对分析予以验证。本文首次考虑系统详细模型对开环模式谐振现象进行HIL 仿真，不仅是HIL 设计在系统谐振现象研究中较为少见的应用，也是开环模式谐振研究的全新拓展和补充。对比既有研究，本文所建HIL 平台不仅考虑了详细的系统模型，是更可靠的时域仿真模型，可以更好地检验控制策略与谐振机理，也保证了实时的仿真速度和与实际装置进行互联测试的能力［15］。

1 HIL平台搭建

开环模式谐振HIL 仿真实验平台由PC 上位机，StarSim 实时仿真器MT6020 和快速控制原型MT1050 三部分组成，实验平台结构如图1 所示。其中MT6020 用来模拟系统拓扑电路， MT1050 对风电背靠背变流器进行控制，其间采用定制接线板进行I/O 接线。上位机分别与控制器和仿真器相连。在时间尺度上采用大小步长混合仿真方法［16］，电路拓扑仿真步长为1 μs，控制系统仿真步长为50μs。

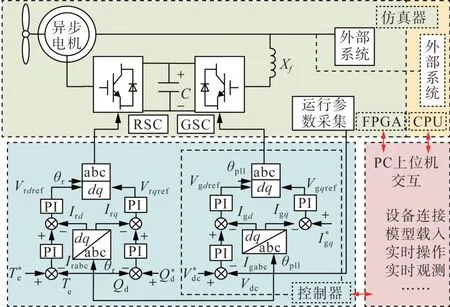
图1 开环模式谐振实验平台结构图Fig. 1 Structure diagram of open-loop mode resonance experimental platform

RSC 外环由转矩控制和无功控制组成，内环由转子侧d、q轴电流控制回路组成［17］。GSC 外环为直流电压控制，内环由网侧d、q轴电流控制回路组成。仿真器将测得的模拟信号输出至控制器，在控制器形成参考电压后，经过SVPWM 调制输出控制信号至位于仿真器的换流器模型上，形成闭环。换流器拓扑结构如图2 所示。现有开环模式谐振研究中均直接使用参考信号Vref表示桥臂端子处产生的平均电压，忽略了换流器的影响［18-19］。

图2 换流器拓扑结构Fig. 2 Topology of converters

在FPGA 中，采用LC 建模方式对电力电子器件进行建模，即当开关闭合时建模为一个很小的电感，当开关断开时建模为一个很小的电容，如图3所示，积分方法为向后欧拉法。LC 建模方式在开关状态改变时会有能量损耗，但就风电机组变流器较低的开关频率而言对整体仿真结果影响很小。

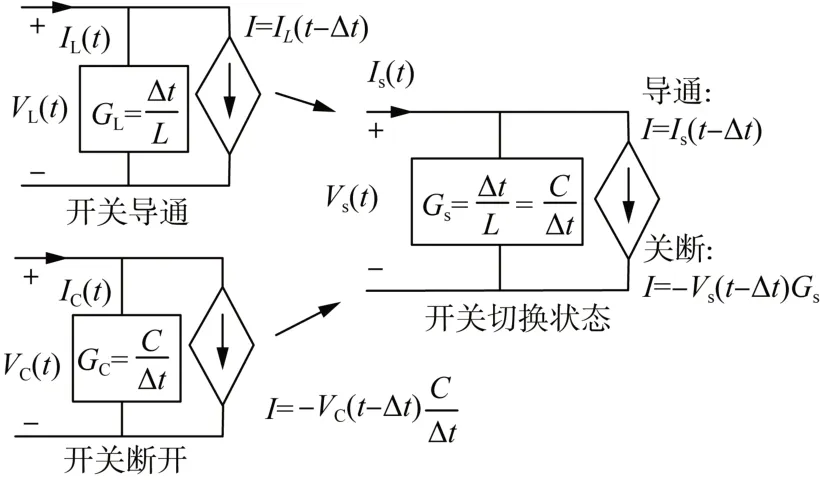
图3 电力电子器件LC建模方式Fig. 3 LC modeling methods for power electronics devices

仿真器含CPU 核，对无需小步长仿真的器件，如分布式电源、滤波器和非主要研究对象等［20］可使用模型分割法将其分配到CPU 大步长并行计算［21］，在硬件资源有限情况下进行更大规模仿真［22］。

按照图1 设计结构搭建如图4 所示半实物实验平台。开环模式谐振体现为子系统间动态交互，与既往研究中状态方程构建的数学模型以及单一软件构建的仿真模型不同，所建立的HIL 模型不在单一仿真计算环境中，HIL 实验中本质参与谐振的DFIG 控制电路与外部系统处于异构设备（控制器-FPGA 或者控制器-CPU），在经过线路传输、数模转换、步长变化之后，这种动态交互作用在一个更为复杂、更贴近实际的运行环境中得到了体现。

图4 HIL实验平台Fig. 4 HIL experimental platform

2 开环模式分析方法

开环模式谐振条件是指闭环互联系统的两个开环子系统中的振荡模式在复平面上距离较近的情况，此时，系统闭环模式有可能会相反方向弹开，导致闭环系统稳定性下降。

2.1 DFIG与外部系统闭环互联模型

设Xd为DFIG 所有状态变量组成的列向量，则DFIG子系统的状态空间模型为：

式中：s为拉普拉斯算子；Ad为DFIG子系统状态矩阵；Βd、Ad、Dd分别为相对应的系数矩阵；ΔYd=[ΔPdΔQd]T为DFIG 输出功率变化量； ΔVt=[ΔVtxΔVty]T为端电压变化量；ΔXd为Xd的变化量。

设Xs为外部系统所有状态变量组成的列向量，则外部子系统的状态空间模型为：

式中：As为外部子系统状态矩阵；Βs、Cs、Ds分别为相对应的系数矩阵；ΔXs为Xs的变化量。

根据输入输出变量的关系，DFIG 并网系统的线性化闭环互联模型可表示为图5形式［23］。

图5 系统闭环互联模型Fig.5 Closed-loop interconnection model of the system

设X为系统所有状态变量组成的列向量，联立式（1）和式（4），得到闭环状态空间模型为：

式中：A为闭环系统状态矩阵；ΔX为X的变化量。

由式（1）和式（4）得出图5 中的开环传递函数H(s)和W(s)为：

式中I为单位矩阵。

2.2 开环模式分析方法

假设λd和λs分别为DFIG 子系统和外部子系统的某一开环模式，则它们分别为H(s)和G(s)的极点，当满足开环模式谐振条件λd≈λs时H(λs)的值很大，ΔYd值也很大，子系统之间动态交互强烈。开闭环模式之间的差值增大，从而影响闭环振荡模式的阻尼。图5所示闭环系统特征方程为［24］：

将H(s)和G(s)展开为留数形式代入式（7）得：

式中：Rd、Rs分别为λd和λs对应的留数；Rdn为λdn（n= 2，3，4，…）对应的留数；Rsm为λsm（m=2，3，4，…）对应的留数。

将闭环互联系统中对应的模式λ̂d代入式（8）可得：

设λc为两开环模式的中点，x为其与开环模式的间距，开环模式谐振条件下，式（9）可近似表达为：

解得：

同理可得，那么闭环模式预测值和可表示为：

由式（12）可以看出，开闭环模式差值取决于开环模式间距以及留数，当Re(λc)时，一个闭环模式会位于复平面右半部，导致系统失稳。

由此得到开环模式分析方法如下。

1）建立图3所示系统互联模型；

2）由式（1）和式（4）中开环状态矩阵Ad和As计算两个子系统的开环模式，判断是否有满足开环模式谐振条件的模式；

3）根据式（12）指标计算出对应闭环模式预估值，判断系统是否失稳。

由于子系统是从并网点进行划分，对所有接入对象具有普适性，因此该方法可等效地运用到其他形式的电力系统中（PMSG 并网系统、光伏并网系统等）稳定性分析，是一种通用分析方法。

3 算例分析与实验

合理假设风电场内部发电机均为1.5 MW 的DFIG，运行特性相同，忽略内部电缆，则可以将其等效为一台DFIG，容量取风电场总和［23］。

3.1 两个DFIG之间的开环模式谐振

当多个并网DFIG 的参数设置不当时可能会在相互之间产生谐振风险［10］。本节按开环模式分析方法主要考虑RSC 内环、GSC 直流电压外环控制环节影响，对图6 所示的系统进行模式分析和HIL 实验验证。风电场内部均含6 台风机，系统参数参见文献［25］，考虑实际情况，DFIG-A 和DFIG-B的控制参数在给定值的基础上始终保有3%的差异设置。

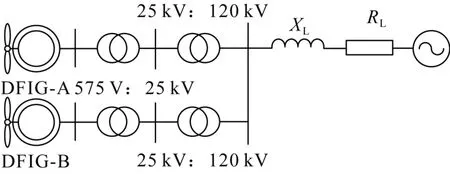
图6 两个DFIG并网算例系统Fig.6 Two example systems with DFIGs grid connected

3.1.1 两个DFIG的RSC内环开环模式谐振

系统中参与开环模式谐振的振荡模式计算结果如表1 所示，λdA和λdB分别为DFIG-A 子系统、DFIG-B 子系统中与RSC 内环控制相关的模式；和分别为闭环系统中与λdA和λdB相对应的振荡模式，由闭环状态矩阵A求得。

表1 相关计算模式Tab. 1 Related calculation modes

表1 中FdA为子系统对的参与度，FdB为子系统对的参与度。λdA和λdB在复平面上相隔较近，该情况下两个子系统极大程度地参与了对方主导的振荡模式，表明此时动态交互作用显著，开环模式谐振导致实部为正，系统失稳。

为更好展示开环模式谐振对RSC内环振荡模式的影响，将DFIG-A 的RSC 无功电流内环参数从kpA= 0.002 5、kiA= 1 逐渐增至kpA= 0.075、kiA=30，计算DFIG-A 和DFIG-B 各自的开闭环模式移动轨迹如图5 所示。当λdA向λdB逐渐靠近时，闭环模式向两边弹出距离增加，系统稳定性下降，而当控制参数继续增大，当λdA远离λdB时闭环模式又逐渐向开环模式靠拢，动态交互减弱，系统稳定性回升。根据式（12）计算的闭环模式预估值以x标出。

在HIL平台中搭建图6所示系统。DFIG-A并网系统载入实时仿真器的底层FPGA，DFIG-A控制电路载入控制器，为节省硬件资源，将DFIG-B 载入仿真器的CPU 中。取DFIG-A 的RSC 无功电流内环参数kpA= 0.02、kiA= 8 和kpA= 0.05、kiA= 20（图7 中点A、B）两个情形，在仿真时间t=5.0 s 时DFIG-A 输出转矩下降20%，0.05 s 后恢复，提取DFIG-A 的有功输出数据并绘制曲线如图8 所示。小方框内为实验波形局部放大图。同时绘制了离线平均模型仿真结果作为对比。由于实时控制器存在时滞［26］，响应略微落后于5.0 s，而离线仿真中可以瞬时响应，因此其切换时间设置在t=5.01 s。

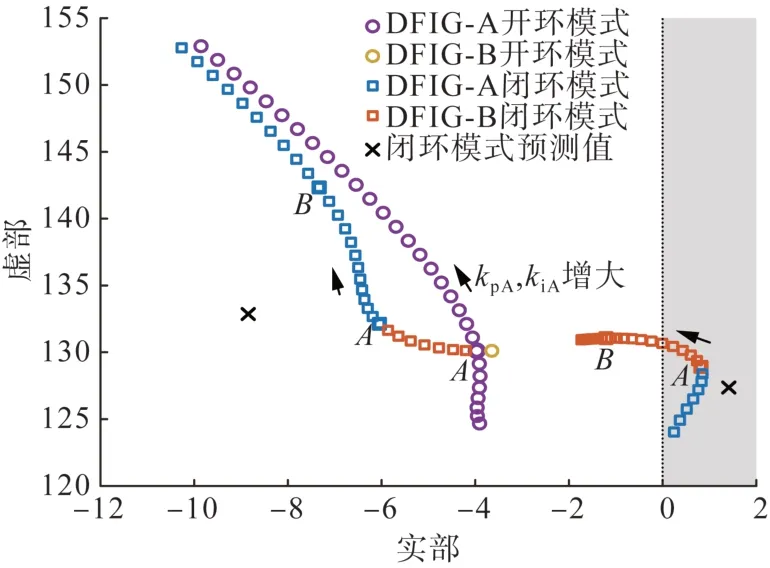
图7 DFIG-A与DFIG-B的RSC内环开环模式谐振Fig. 7 Open loop mode resonance of RSC inner loop between DFIG-A and DFIG-B

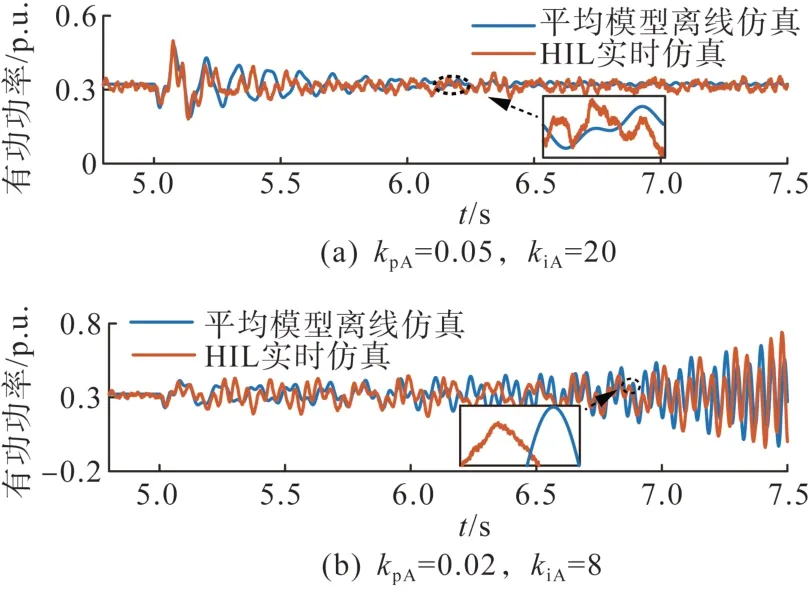
图8 kpA、kiA变化时DFIG-A有功功率动态响应Fig. 8 Dynamic response of DFIG-A active power when kpAand kiAchange

由图8 可看出，kpA= 0.05、kiA= 20 时，系统发生约21 Hz 振荡后回稳，与B点振荡模式-1.21+131.1 i 相符，此时开环模式相隔较远，谐振作用弱；kpA= 0.02、kiA= 8 时，系统发生频率20 Hz 的SSO，与A点振荡模式相符，SSO 由两个DFIG 的RSC 内环开环模式谐振引起。开环模式分析的结果得以验证。图9 给出点A参数下交流端电流电压的变化情况。

图9 点A情况下交流端电流电压的变化Fig.9 Variation of AC current and voltage at point A

3.1.2 两个DFIG的直流电压外环开环模式谐振

DFIG 并网系统在直流电压时间尺度上也存在着振荡风险［27］，现从开环模式谐振角度分析其成因。将RSC内环控制参数调整为kp= 0.08，ki= 8，直流电压外环控制参数调整为kp*= 0.02，ki*= 8。系统直流电压外环振荡模式及参与因子计算结果如表2 所示。两DFIG 直流电压外环开环模式在复平面上相隔较近，从参与因子可以看出此时DFIG-A与DFIG-B 动态交互作用强烈。开环模式谐振导致位于复平面右半部分，系统失稳。

表2 相关计算模式Tab. 2 Related calculation modes

为展示直流电压外环产生谐振的过程，将DFIG-A 的直流电压外环参数从kpA*= 0.002 5、kiA*= 1 逐渐增至kpA*= 0.075、kiA*= 30，计算得到DFIG-A 和DFIG-B 各自的开闭环模式移动轨迹如图10 所示。当λdA向λdB逐渐靠近时，右侧闭环模式阻尼不断减弱，系统稳定性下降，在C点最终引发失稳。当DFIG-A 的控制参数继续增大时，λdA远离λdB，谐振逐渐减弱，系统重回稳定。

图10 DFIG-A与DFIG-B的直流电压外环开环模式谐振Fig.10 Open loop mode resonance of DC voltage outer loop between DFIG-A and DFIG-B

使用3.1.1 小节中搭建的系统，取直流电压外环参数kpA*= 0.02、kiA*= 8 和kpA*= 0.05，kiA*=20（图10 中点C、D）两个情形，在仿真时间t=5.0 s时DFIG-A 输出转矩下降20%，0.05 s 后恢复，提取DFIG-A 的有功输出数据并绘制曲线如图11 所示。同样绘制了离线平均模型仿真结果作为对比。由图11 可以看出，kpA*= 0.05，kiA*= 20 时，系统发生6.8 Hz 振荡后回稳，与D点振荡模式-1.67+40.6 i 相符，此时开环模式相隔较远，谐振作用弱；kpA*= 0.02，kiA*= 8 时，系统发生频率5.5 Hz 的振荡失稳，与C点振荡模式相符，由开环直流电压外环模式谐振引起。开环模式分析结果得以验证。图12给出了点C情况下交流端电流电压的变化情况。

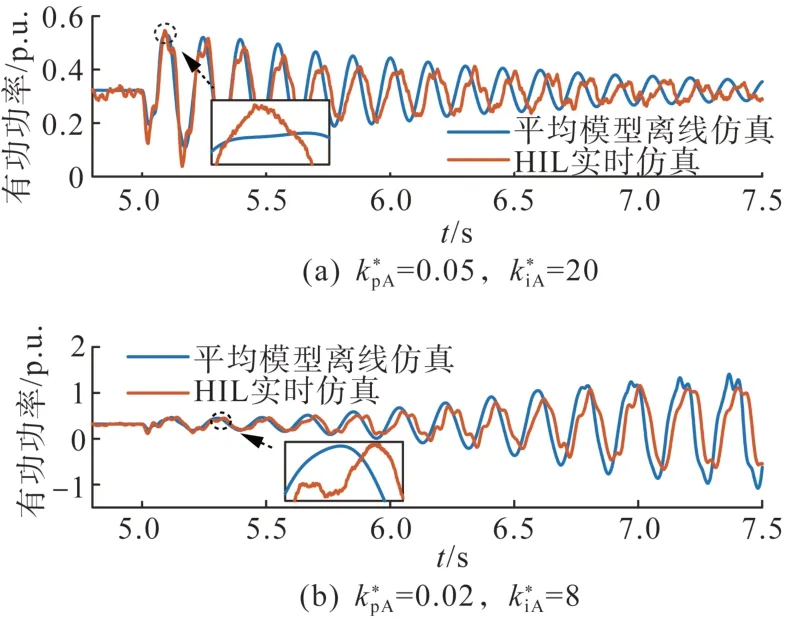
图11 kpA*，kiA*变化时DFIG-A有功功率动态响应Fig.11 Dynamic response of DFIG-A active powers when kpA*and kiA*change

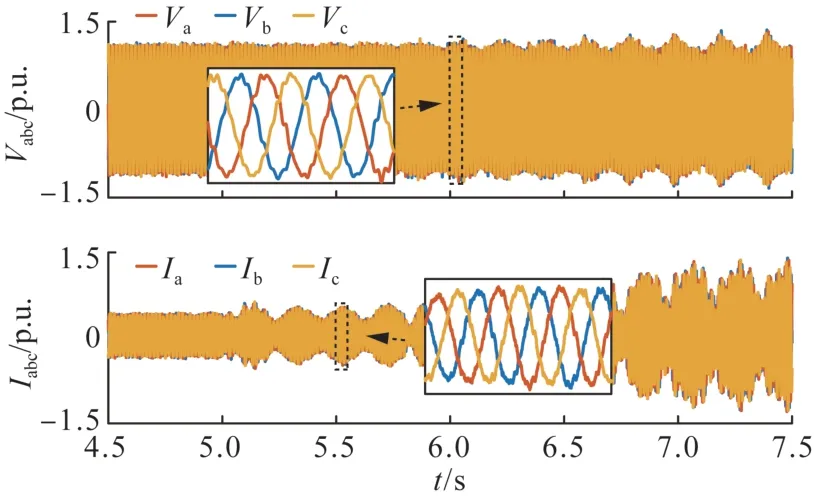
图12 点C情况下交流端电流电压的变化Fig.12 Variation of AC current and voltage at point C

3.2 DFIG与串补之间的开环模式谐振

DFIG 经串补并网时，RSC 控制系统可能与串补产生开环模式谐振［28-29］。本节对沽源双馈风电场串补输电系统（如图13 所示）进行开环模式谐振风险分析。系统参数参见文献［30］，采取相同的系统等效建模策略，假设风电场内有500 台DFIG 输出功率。

图13 沽源DFIG风电场经串补并网等值示意图Fig.13 Schematic diagram of Guyuan DFIG wind farm connected to the grid through series compensation

将串补度调整为kc= 0.4 进行模式分析。系统中参与开环模式谐振的振荡模式计算结果如表3 所示，λd为DFIG 子系统中与RSC 电流内环控制相关的模式，λr为外网子系统中与串补相关的模式；和为闭环系统中与λd和λr相对应的振荡模式，由闭环状态矩阵A求得，Fd为子系统对的参与度，Fr为子系统对的参与度。

表3 相关计算模式Tab. 3 Related calculation mode

引起阻尼大幅减弱、系统失稳的原因是开环模式在复平面相隔较近，子系统谐振作用加剧，其强度可用参与因子衡量。显然，开环模式谐振条件下，两个子系统很大程度地参与了对方主导的振荡模式，表明此时动态交互作用显著。

为更好展示开环模式谐振对系统振荡模式的影响，将kc从0.05 逐渐增大至0.9，计算得到DFIG和串补各自的开闭环模式移动轨迹如图14 所示，灰色区域为不稳定域。当λr向λd逐渐靠近时，闭环模式向两边弹开，右侧振荡模式阻尼减弱，系统稳定性下降。

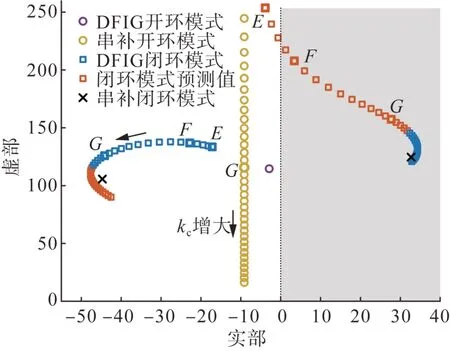
图14 调整kc时RSC内环与串补的开环模式谐振Fig.14 Open-loop mode resonance between RSC inner loop and series compensation when adjusting kc

在HIL 平台中搭建图13 所示系统。DFIG 并网系统载入实时仿真器，DFIG 控制电路载入控制器。分别取线路串补度kc=0.05，0.15，0.4 三种情形（图14 中点E、F、G），设置仿真器内部信号源在t=6.0 s 切入串补，提取DFIG 的有功功率输出数据并绘制曲线如图15所示。

图15 kc变化时DFIG有功功率动态响应Fig.15 Dynamic response of DFIG active power when kc changes

由图15 可以看出，kc= 0.05 时，系统发生42 Hz 振荡后回稳，与E点振荡模式-3.87+253.6 i 相符；kc= 0.15 时，系统发生35 Hz 的SSO，与F点振荡模式3.43+207.8 i 相符，开环模式谐振影响增强；kc= 0.4 时，系统发生负阻尼极大的SSO，与G点振荡模式相符，此时子系统间强动态交互使系统快速失稳。开环模式分析结果得以验证。图16给出了点G实验条件下交流电流电压的变化。

图16 点G情况下交流端电流电压的变化Fig.16 Variation of AC current and voltage at point G

4 结论

本文针对开环模式谐振理论研究在实验方面的不足做出了一系列补充。主要贡献是搭建HIL 实时仿真平台对详细模型的DFIG 并网系统开环模式谐振现象进行实验，最终达成了两者的双向验证，实验结果既支持了实时仿真平台的准确性，也验证了开环模式分析的有效性。

1）搭建了DFIG接入电力系统的HIL实时仿真实验平台，可为风电并网系统稳定性研究提供值得参考的模型和搭建方式，并且给出了更适用于实时仿真的风机控制参数，可反馈到理论研究的参数设置中。

2）以两个DFIG 接入系统发生SSO、沽源DFIG风电场串补输电系统SSO 为例，从开环模式谐振的角度分析其成因，并进行HIL 实验验证，实验结果与开环模式分析相符，为该理论提供了有力的实验数据支撑，实际工程中需要考虑到该风险。通过参数的相应整定可以有效避免开环模式谐振对系统稳定性的影响。