柔性直流输电系统高频谐振自适应抑制策略

王延纬，刘宇明，杨荣照，钟明明，林建熙，付超，易杨，秦颖婕，周保荣

（1. 广东电网有限责任公司电力调度控制中心，广州 510600；2. 南方电网科学研究院，广州 510663）

0 引言

柔性直流输电（MMC-HVDC）具有有功功率、无功功率解耦控制的灵活控制特点，在大容量、远距离的电力输送中有着广泛应用［1-4］。近年来随着多个柔性直流系统工程的投入运行，柔性直流相关的稳定性问题也逐渐凸显，柔性直流系统的高频谐振现象也频频出现［5-8］。2013 年德国海上风电柔性直流送出工程在运行过程出现了250～350 Hz 的谐波谐振［9］；2015年法西联网工程在交流网架拓扑结构发生变化的情况下，变流器投入运行后出现了1.7 kHz 高频谐振［10］；2017 年鲁西背靠背直流工程在电网运行方式发生变化、短路比减小的情况下，发生了1 270 Hz 左右的高频谐振［11］；2018 年渝鄂直流工程在进行试验时，两侧分别出现了1.8 kHz和0.7 kHz的高频振荡［12-14］。由此造成的输电中断给系统的稳定运行带来了巨大的挑战，因此亟需提出抑制策略解决高频谐振问题。

目前高频谐振抑制策略的研究还处于起步阶段。文献［15］在原有控制器的基础上附加了谐波电流环，改变了柔性直流变流器在谐振频率处的谐波阻抗。文献［16］分析得出电压前馈环节对柔性直流的高频谐振影响较大，提出在电压前馈环节串入二阶低通/带通滤波器来减小高频信号的影响，虽然这两种策略能够抑制高频段的谐振，但会恶化中频段的阻抗特性，可能导致系统产生新的谐振频率。文献［17］提出在电压前馈环节串入带阻滤波器的方式来抑制高频谐振，但设计时考虑的带宽较大，未能发挥带阻滤波器精准控制的优势。系统的网架结构多变，高频谐振频率也会随之变化，且在系统分析中采用输电线路分布参数时，会存在多个谐振风险点。文献［18］提出了基于自适应参数的陷波器控制方法，但该策略只考虑了系统存在单谐振频率的情况。文献［19］提出了级联陷波器的方式来分别抑制不同频率的高频谐振，但该策略的带阻频段为固定值，未能适应谐振频率多变的问题。

综合上述分析，现有的高频谐振抑制策略分别从变流器侧控制系统和电网侧两方面进行研究，但大部分文献场景分析较为简单，其中受端交流电网采用简单RLC等值网络，不能准确反映交流系统高频段的阻抗特性，导致提出的谐振抑制策略在多变的网络拓扑及运行方式时适用性较差。因此针对交流系统网络拓扑及运行方式多变情况下可能存在多谐振频率点及谐振频率多变的高频谐振自适应抑制策略还需要进一步深入研究。

针对现有高频谐振抑制策略的缺陷，本文提出了基于自适应带阻滤波器的高频谐振抑制策略。通过自适应调节附加带阻滤波器的数量及频率参数以适应交流系统网络拓扑多变产生的多谐振频率点及谐振频率多变的问题。最后通过电磁暂态仿真验证了本文所提出的抑制策略在系统不同运行方式下控制作用的有效性与灵活性，保证了系统安全稳定运行。

1 高频谐振机理分析

1.1 高频谐振稳定性判据

阻抗分析法在研究直流变流器馈入受端交流系统的阻抗稳定性时，从端口看过去，分为变流器和受端电网两个子系统，分别建立各自的阻抗模型［20］，最终获得柔性直流馈入受端电网的阻抗等效电路［21-22］，具体如图1所示。

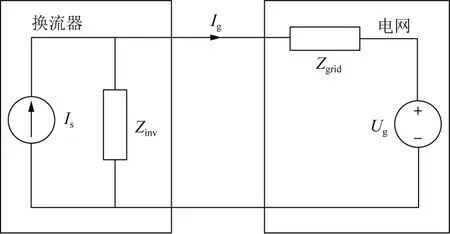
图1 柔性直流馈入受端电网的小信号阻抗电路图Fig. 1 Small signal impedance equivalent circuit diagram of VSC-HVDC feeding into the receiving end grid

根据图1 的电路关系可以得到注入电网电流Ig表达式为：

式中Is(s)、Ug(s)、Zgrid(s)和Zinv(s)分别为柔性直流等值电流、受端电网等值电压、受端电网的等值阻抗和柔性直流等值阻抗。

通常，设计要求并网逆变器能单独稳定运行，因此注入电网电流Ig（s）的稳定主要取决于式中第二项，即1/［1+Zgrid（s）/Zinv（s）］。为保证并网逆变器馈入系统的稳定，需要电网阻抗与并网逆变器的输出阻抗比值Zgrid（s）/Zinv（s）满足奈奎斯特稳定判据，即当变流器等值阻抗与交流系统等值阻抗的幅值一致，且对应的相位差大于180 °时，系统在对应频率下存在谐振失稳风险。

1.2 柔性直流变流器阻抗模型

本文以鲁西背靠背直流为例，其控制结构框图如图2 所示，本文采用的柔性直流变流器阻抗模型见文献［23-24］，其详细的等值阻抗表达式如式（2）所示。

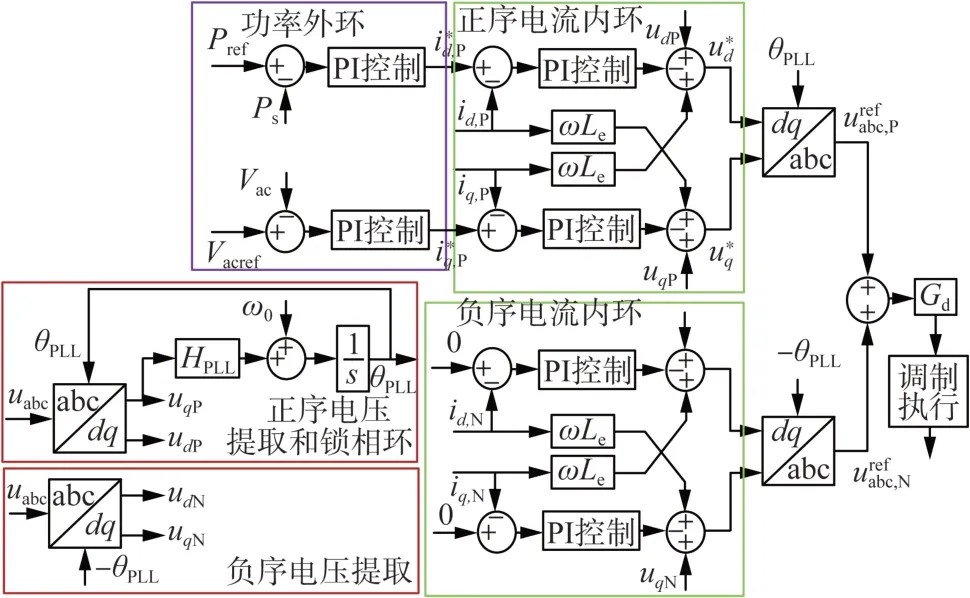
图2 柔性直流的控制器结构框图Fig. 2 Controller diagram of MMC-HVDC

式中：Gi为电流内环PI 控制器的传递函数；Gsd为1/4 工频周期滤波环节的传递函数；Kd为电流内环解耦系数；Gsv、Gsi分别为电压和电流采样环节的传递函数；GPQ为功率外环PI 控制器的传递函数；Gd为控制系统总的延时；GPLL为锁相环的传递函数；V1、ω1分别为交流电压幅值和角速度；上标“+”、“-”分别代表因坐标变换导致的频率的正负偏移；I1为交流电流幅值；φi为交流侧电压、电流的相角差；L为柔性直流等值电感；iq0、id0分别为d、q轴稳态电流。

系统总延时过程Gd采用延时环节和零阶保持器传递函数的乘积来表示，具体如式（3）所示。

式中：Td为系统延时；Ts为零阶保持器采样时间。

由于变流器控制中不同控制环节频率带宽特性不同，本文主要针对高频频带展开谐振分析。对带宽较低的模块频率特性进行简化，例如锁相环、功率外环、电流内环正负序独立及解耦控制，推导可得高频段的谐波阻抗表达式为：

1.3 交流系统阻抗模型

本文根据鲁西背靠背直流工程搭建了一个受端交流系统分析模型，具体拓扑结构如图3 所示，其中输电线路选用分布参数里的Bergeron模型［25］，网络拓扑的详细参数见表1—2［26］。

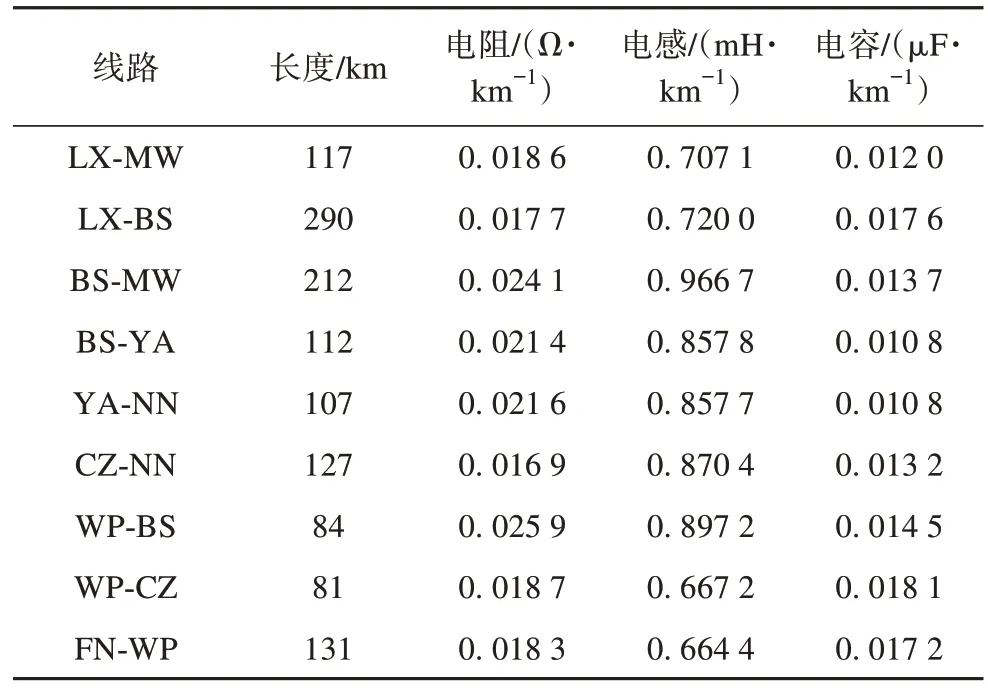
表1 受端交流电网输电线路基频参数Tab. 1 Fundamental frequency parameters of AC power grid transmission lines at the receiving end

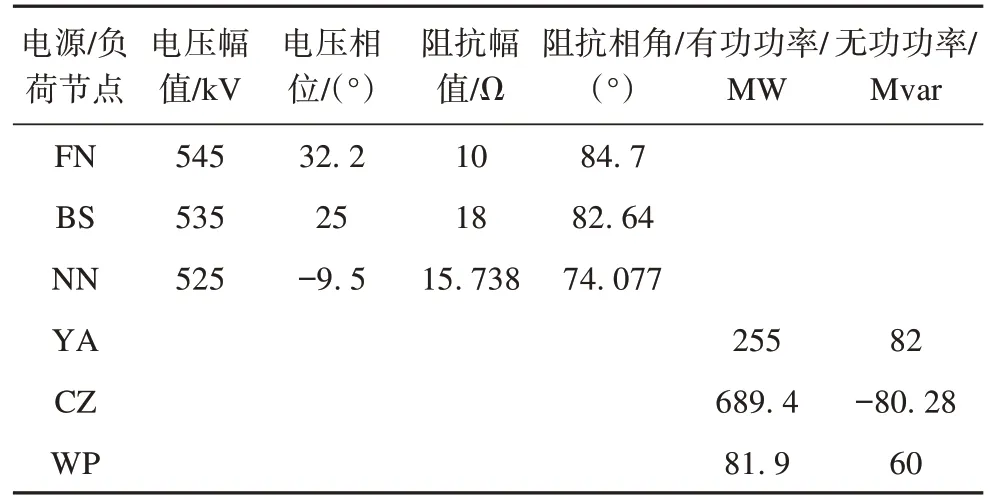
表2 受端交流电网电源及负荷参数Tab. 2 Power and load parameters at the AC receiving grid

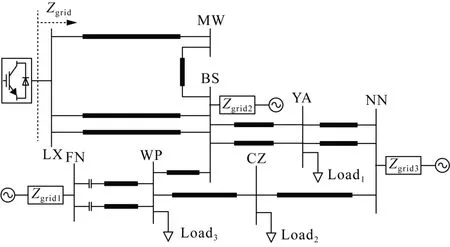
图3 交流系统拓扑结构图Fig. 3 AC system topology diagram

输电线路采用集中的π 形等效电路表示，输电线路的分布参数模型首端m 的电压和电流以及末端n的电压电流满足式（5）。

式中：̇、̇分别为电压和电流相量；下标m 和n分别表示首端和末端；Z和Y分别为输电线路总阻抗和总导纳；为输电线路波阻抗。

正常运行工况下对变流器系统侧端口展开的交流系统阻抗频率扫描结果如图4所示。由图4可知，对于较复杂的交流电网拓扑，系统存在多个谐振峰，与柔性直流变流器阻抗相交并满足高频谐振稳定性判据的交点数也增多。

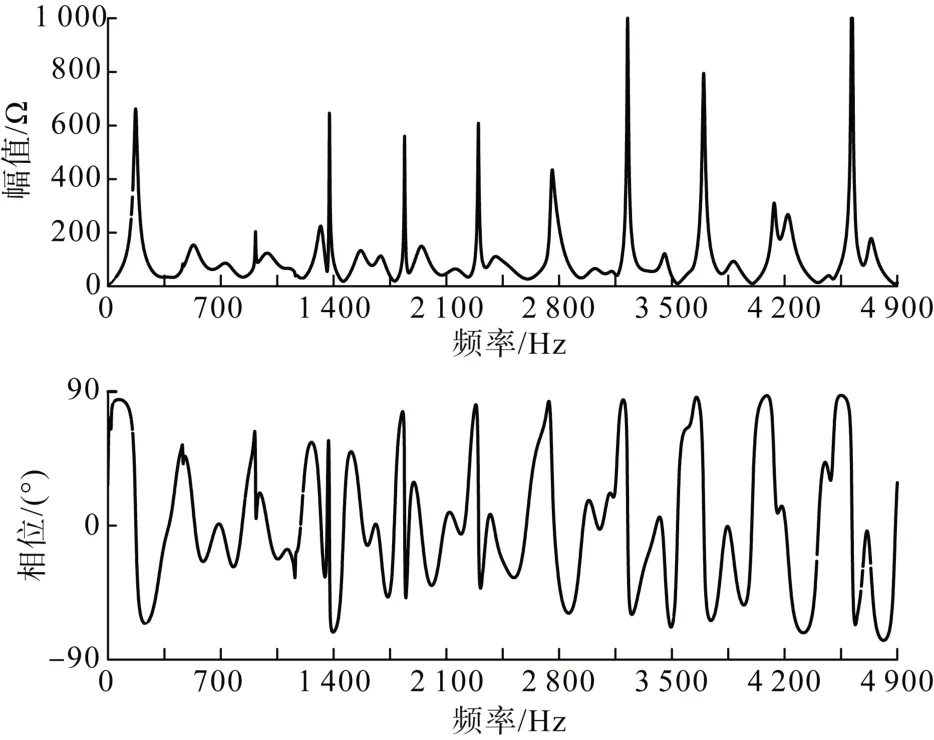
图4 交流系统阻抗频率特性曲线Fig. 4 Impedance frequency characteristic curves of AC grid

2 传统的附加滤波器的高频谐振抑制策略

为抑制高频谐振问题，通常可采取在变流器电压前馈环节附加滤波器的措施，包括低通和带阻滤波器。本节针对传统附加控制展开了对比分析。

2.1 附加二阶低通滤波器的高频谐振抑制策略

通过对变流器等值谐波阻抗分析可知，变流器阻抗特性曲线的负阻尼主要由分母中的系统延时项Gd、Gsv相位周期性变化引入。通过在电压前馈环节引入二阶低通滤波器可削弱系统延时项在高频段的增益，进而提升系统稳定裕度。二阶滤波器表达式GLP为：

式中：ξ为阻尼比；ωn为自然频率。引入二阶低通滤波器后，阻抗模型表达式为：

考虑设置低通滤波器带宽为200 Hz，对比分析了电压前馈串入二阶低通滤波环节前后的阻抗特性，具体如图5 所示。串入二阶低通滤波器对变流器中高频段的阻抗特性影响较大，虽然消除了高频段的阻抗幅值峰和负阻尼现象，但在中频段区域引入了负阻尼问题，当受端交流系统阻抗在中频段匹配上时依然会引发谐振。

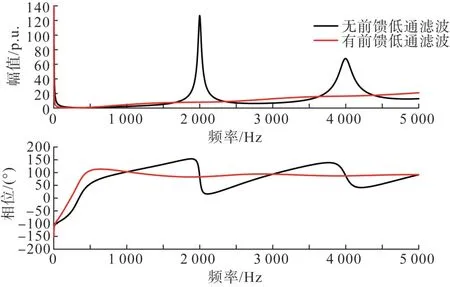
图5 电压前馈串入二阶低通滤波环节前后柔性直流阻抗曲线对比图Fig. 5 Impedance comparison curves of MMC-HVDC considering second-order LPF in voltage feedforward

2.2 附加带阻滤波器的高频谐振抑制策略

与附加二阶低通滤波器策略类似，在电压前馈环节中串入一个带阻滤波器，其表达式Gfilter-B为：

式中f0为带阻滤波器的中心频率。串入带阻滤波器后，阻抗模型表达式为：

考虑设置带阻滤波器的中心频率为1 250 Hz，分析电压前馈串入带阻滤波环节前后阻抗曲线对比结果，如图6所示。

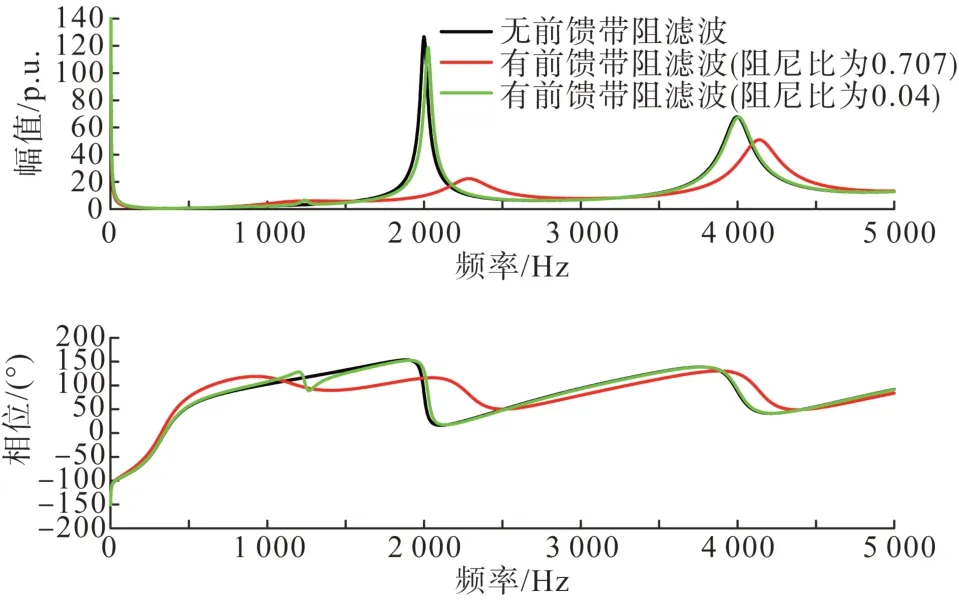
图6 电压前馈串入带阻滤波环节前后柔性直流阻抗曲线对比图Fig.6 Impedance comparison curves of MMC-HVDC considering band-stop filter in voltage feedforward

与串入二阶低通滤波器不同，带阻滤波器仅影响频带范围内的阻抗特性。而当阻尼比取值较大时，同样会使得负阻尼特性向中频段偏移。当阻尼比取值较小时，对其他频段的阻抗特性影响较小，使控制更有针对性。由图6 可知，当阻尼比为0.04时，附加控制仅在中心频率1 250 Hz 附近产生影响。

3 基于自适应带阻滤波器的高频谐振抑制策略

3.1 高频谐振抑制策略的整体设计

随着受端交流电网运行方式或者电网强度等系统条件的变化，交流系统的等值阻抗也相应变化，这就会导致高频谐振频率也会随之变化，使得串入固定参数的带阻滤波器无法达到抑制效果。同时根据图4 中的交流系统阻抗特性，实际柔性直流并网系统中可能存在多个高频谐振频率，为解决这个问题，需要根据实际谐振频率点的数量来选择级联带阻滤波器的数量。在电压前馈级联带阻滤波器的传递函数定义为Gfilter-B1，可得：

式中：m为级联带阻滤波器的数量；fi为第i个带阻滤波器的中心频率；ξi为第i个带阻滤波器的阻尼系数。

本文考虑对派克变换前的电压前馈量级联带阻滤波器，柔性直流换流器交流侧等值谐波阻抗表达式为：

考虑系统总延时为500 μs，分析引入不同附加中心频率带宽为100 Hz的带阻滤波器后柔性直流等值谐波阻抗的特性，结果如图7 所示。分析可知，附加带宽较小的带阻滤波器仅对中心频率点附近的阻抗特性产生影响，使柔性直流等值阻抗在中心频率的幅值会产生一个小的尖峰，且带宽范围内的相角特性会呈现先增加后减小再增大的趋势。

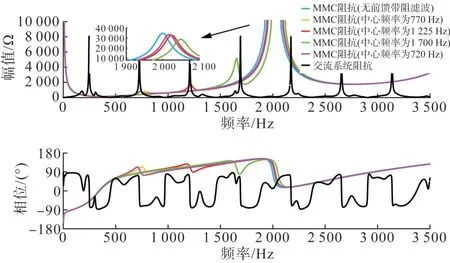
图7 附加带阻滤波器前后柔性直流换流器等值谐波阻抗特性对比图Fig. 7 Impedance comparison curves of MMC-HVDC considering different band-stop filters in voltage feedforward

通过对比中心频率分别为770 Hz、1 225 Hz 和1 700 Hz 的变流器等值阻抗特性曲线，可以发现与交流系统等值阻抗的交点随着频率的减小而逐渐从幅值尖峰的右侧往左侧移动，反而使变流器阻抗与交流系统等值阻抗的相位差增大，导致带阻滤波器的抑制效果变差。因此当附加的带阻滤波器中心频率较低时，为充分发挥带阻滤波器的性能，考虑将中心频率向左偏移其带宽的1/2。通过对比中心频率为770 Hz 和720 Hz 的阻抗曲线，与交流系统阻抗交点相位差由185.1 °减小为155.7 °，可见该措施可以提升带阻滤波器的抑制效果。

为了根据系统实际的高频谐振情况自适应地调节级联带阻滤波器的数量及其参数，本文提出了基于自适应带阻滤波器的高频谐振抑制方法，其整体的逻辑框图如图8所示。

图8 基于自适应带阻滤波器的高频谐振抑制策略的整体逻辑框图Fig. 8 Overall logic diagram of high frequency resonance suppression strategy based on adaptive band-stop filter

该方法在串入带阻滤波器的基础上实现了高频谐振频率检测及分析、高频谐振判别及使能、滤波器参数计算及设定。首先根据傅里叶分析提取得到高频谐振频率及幅值，根据分析结果判断每一个频率分量幅值是否达到预设的阈值，以此来激活自适应带阻滤波器的高频谐振抑制策略，最后根据谐振频率，自适应设置带阻滤波器的参数。通过自适应带阻滤波器的高频谐振抑制方法可实现实际电网多运行工况下的高频谐振抑制。

3.2 高频谐振频率检测及分析模块

该模块包含快速傅里叶变换（fast Fourier transform，FFT）模块和谐振频率分段及提取模块。图9 为高频谐振频率检测及分析模块的流程图。其具体步骤如下。

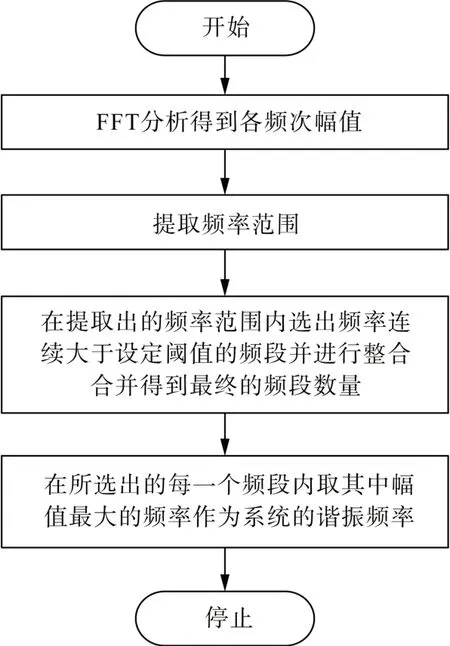
图9 谐振频率检测模块的流程图Fig. 9 Process diagram of resonant frequency detection module

1）FFT 快速傅里叶分析：考虑10 kHz以内的高频谐振抑制，因此考虑FFT 采样频率fs及分辨率fres分别为20 kHz、25 Hz。

2）提取频率范围：为避免低次频率分量对策略带来影响，频率分量只提取大于300 Hz的频率分量进行后续的计算分析。

3）对谐振频率进行分段，取其中连续成立的频率分量作为一个频段，设定频率分量幅值阈值。当系统中提取的高频分量大于设置的阈值时则判定为系统发生了谐振。为确保所提策略具有足够的灵敏度，能够在高频谐振发生后迅速投入，又不会因为高频噪声分量而导致误动作，考虑设置阈值为工频分量幅值的2%～5%；其次开始判断每一个频率分量是否大于设定的阈值，取其中连续成立的频率分量作为一个频段，而考虑到存在相邻频段之间仅相差几个分辨率的间隔，则判定其应该属于同一频段，故进行整合合并，得到最终的频段数量。

4）在每一个频段内取其中幅值最大的频率作为系统的谐振频率，最终将频段数量及谐振频率送入判断及使能模块。

3.3 高频谐振判别及使能模块

图10 为高频谐振判别及使能模块的算法流程图，具体步骤如下。

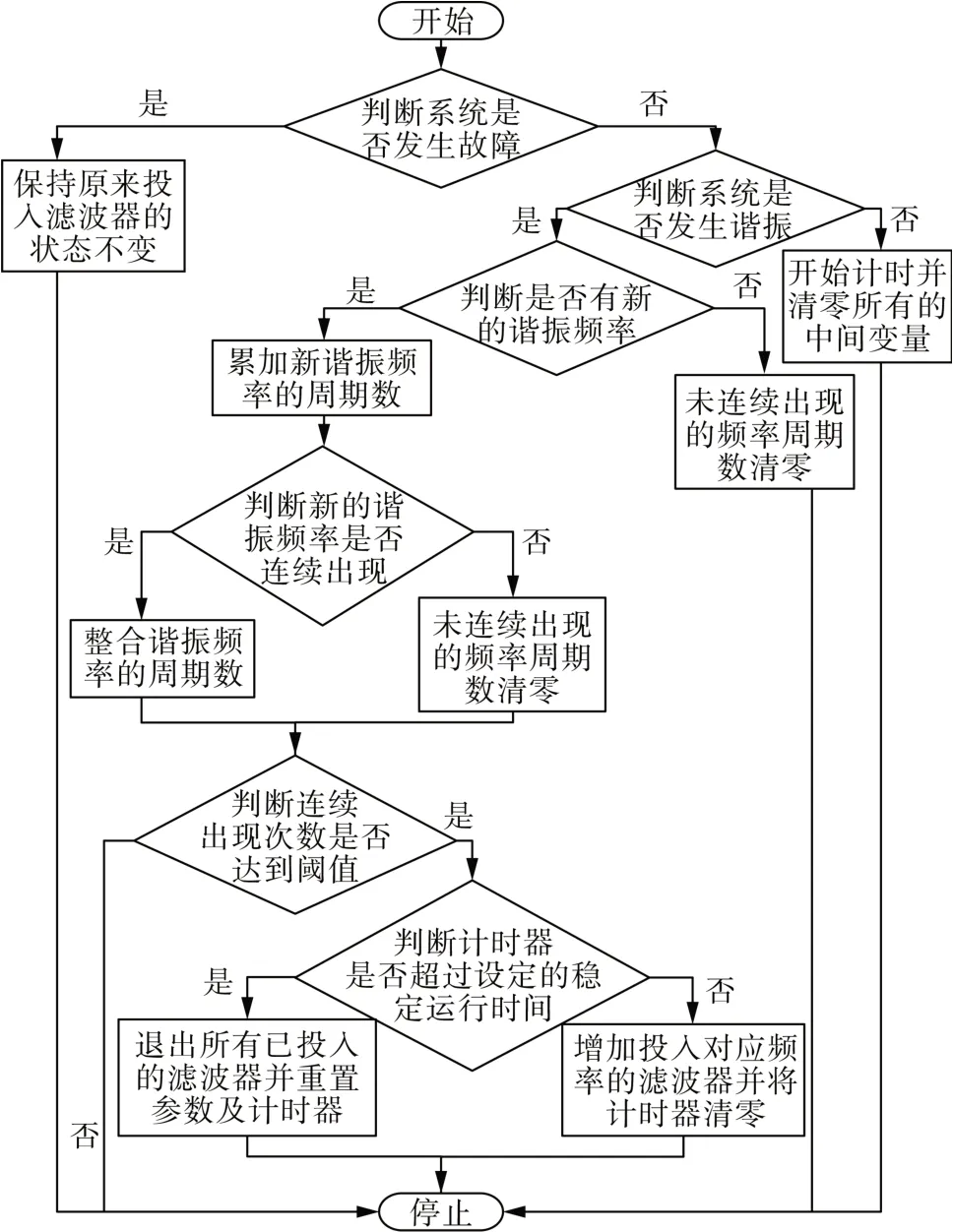
图10 高频谐振判别及使能模块的流程图Fig. 10 Process diagram of high frequency resonance discrimination and enabling module

1）判断系统是否发生故障。当系统处于故障暂态过程中时，系统会存在一些谐波分量，对于谐振频率的判断会产生影响。因此当检测到系统发生故障或其他非正常运行状态时，高频谐波判别模块将闭锁，同时保持已投入滤波器状态不变；当系统未发生故障时，则继续执行步骤2）。

2）判断系统是否发生谐振。当系统未发生谐振，则启动计时器计时，并清零所有中间变量，程序结束；当系统发生谐振则继续执行步骤3）。

3）判断是否有新的谐振频率产生。当没有新的谐振频率产生时，则将未连续出现的谐振频率的统计周期数清零，程序结束；当系统有新的谐振频率产生时，则将新出现的谐振频率的统计周期数加1，并继续执行步骤4）。

4）判断新的谐振频率是否连续出现。当在上一周期出现的谐振频率未再次出现时，则将未连续出现的谐振频率统计周期数清零；当在上一周期出现的谐振频率或临近频率出现时，则将谐振频率相临近的统计周期数进行整合合并，并继续执行步骤5）。

5）判断谐振频率统计周期数是否达到阈值，如本文设定高频谐振持续时间至少200 μs，本文采用的周期为50 μs，因此谐振频率的统计周期数阈值设定为4。当均未达到阈值时，则保持已投入滤波器状态不变，程序结束；当存在谐振频率的统计周期数达到阈值，则继续执行步骤6）。

6）判断计时器的计时是否超过设定的系统稳定运行时间。当计时超过了设定的稳定运行时间，则认为此时新产生的谐振频率是因为系统的运行方式发生变化导致的，需要将所有已投入的滤波器退出，重新检测新的谐振频率，同时计时清零；当计时未超过设定的稳定运行时间，则认为此时系统存在多个谐振频率点，继续增加投入抑制新谐振频率的滤波器，同时将计时器清零。最终将需要投入的滤波器个数及谐振频率送入滤波器参数计算及设定模块。

3.4 滤波器参数计算及设定模块

根据带阻滤波器的表达式（10），每个带阻滤波器有两个参数，分别是中心频率和阻尼比。根据图7 对带阻滤波器频率特性的分析，当系统的谐振频率较高时，不需要对带阻滤波器的中心频率进行偏移，直接将上一模块得到的谐振频率作为滤波器的中心频率；而当谐振频率较低时，则需要对带阻滤波器的中心频率进行偏移，此时将带阻滤波器的中心频率设定为谐振频率减1/2 倍的带宽；带阻滤波器的阻尼比则根据式（12）计算得到。

式中fbw为带阻滤波器的带宽，本文中带宽fbw选取为100 Hz。

4 仿真验证

4.1 仿真系统及场景的设计

为验证本文所提的高频谐振抑制策略，根据图3 所示的网络拓扑结构，在PSCAD/EMTDC 平台上搭建了电磁暂态仿真模型。柔性直流系统仿真的初始条件及系统参数如表3所示。

表3 柔性直流输电系统参数Tab. 3 Parameters of VSC-HVDC transmission system

在本文中共设置了2 种不同的案例进行仿真验证，具体如下。

1） 案例1：受端交流系统在3 s时LX-MW 输电线路断开，LX-BS单回输电线路LX端断开。

2） 案例2：具体为系统在3 s 时LX-BS 输电线路一回完全断开，一回LX 端断开，而后在5.9 s时将LX-BS输电线路一回重新投入运行，仅保留一回在LX 端断开，然后在6 s 时将LX-MW 输电线路断开。

同时本文选择了3 种常见的抑制策略与本文所提的抑制策略进行比较分析，分别为：

1） 策略1：2.1 节中附加二阶低通滤波器抑制策略；

2） 策略2：2.2节中附加带阻滤波器抑制策略；

3） 策略3：文献［18］提出的基于自适应陷波器抑制策略；

4） 策略4：本文所提出的基于自适应带阻滤波器抑制策略。

4.2 基于自适应带阻滤波器抑制策略的仿真验证

4.2.1 柔性直流系统频率阻抗扫描验证

仿真中通过在柔性直流端口注入测量信号，测量端口的响应电压、电流进而扫描计算柔性直流系统的并网频率阻抗特性，结果如图11 所示。通过与理论分析模型对比可知，频率扫描结果与理论曲线基本贴合，进一步验证了推导模型的准确性。同时，通过与交流系统阻抗匹配，当柔性直流系统未投入任何抑制策略时，系统存在1 225 Hz 和1 700Hz两个谐振频率。

图11 案例1中柔性直流阻抗与交流系统阻抗曲线图Fig. 11 Impedances of MMC-HVDC and AC system in case 1

4.2.2 案例1仿真对比分析

考虑投入策略1，柔性直流输电系统的仿真结果如图12 所示。通过仿真曲线与频谱分析可知，系统中1 225 Hz 和1 700 Hz 的高频谐振成分被有效抑制了，但在系统中引入了750 Hz的高频谐振，即附加二阶低通滤波器的抑制策略并不能完全抑制全频段的谐振，会使得柔性直流的等值阻抗的中频段出现负阻尼，与前文分析一致。因此，该策略适用于系统存在单一谐振频率点或者系统在中频段不存在谐振频率点的情况。

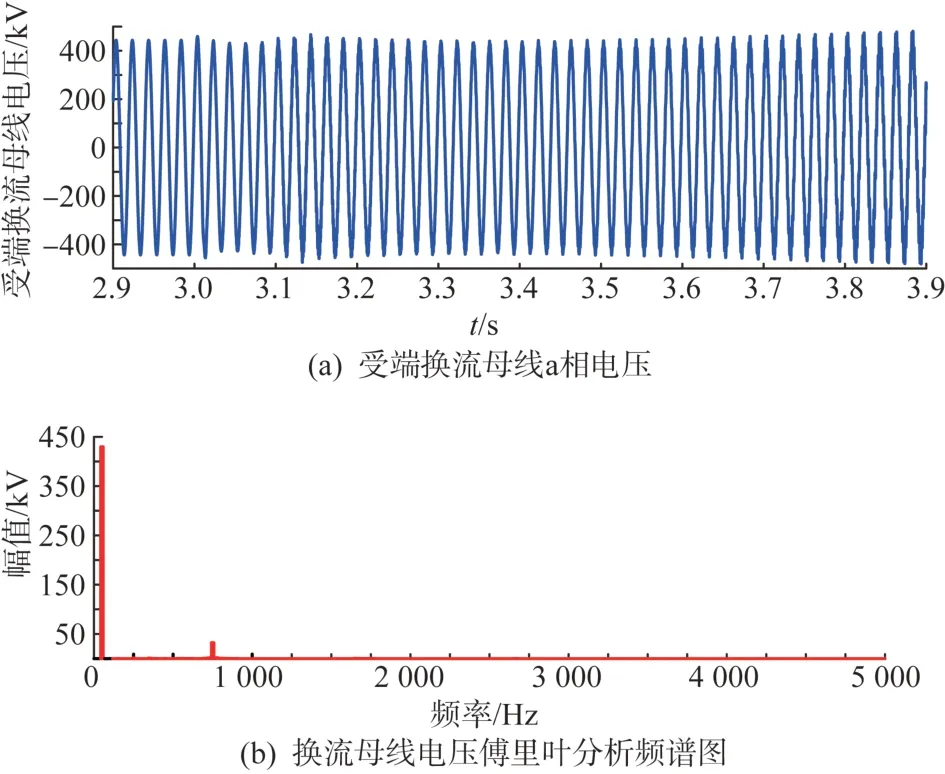
图12 案例1中投入策略1时的仿真结果Fig. 12 Simulation results when implementing strategy 1 in case 1

考虑投入策略2，柔性直流输电系统的仿真结果如图13 所示。通过仿真曲线与频谱分析可知，系统在1 225 Hz 和1 700 Hz 的高频谐振被抑制了，同样系统在750 Hz也产生了高频谐振。可见该策略能够抑制在中心频率附近的高频谐振，但该策略为了获得较大的带宽，阻尼比取值较大，会使得柔性直流其他频段的阻抗特性产生较大的影响，而触发新的高频谐振。因此该策略更适用于系统存在单一谐振频率点的情况。

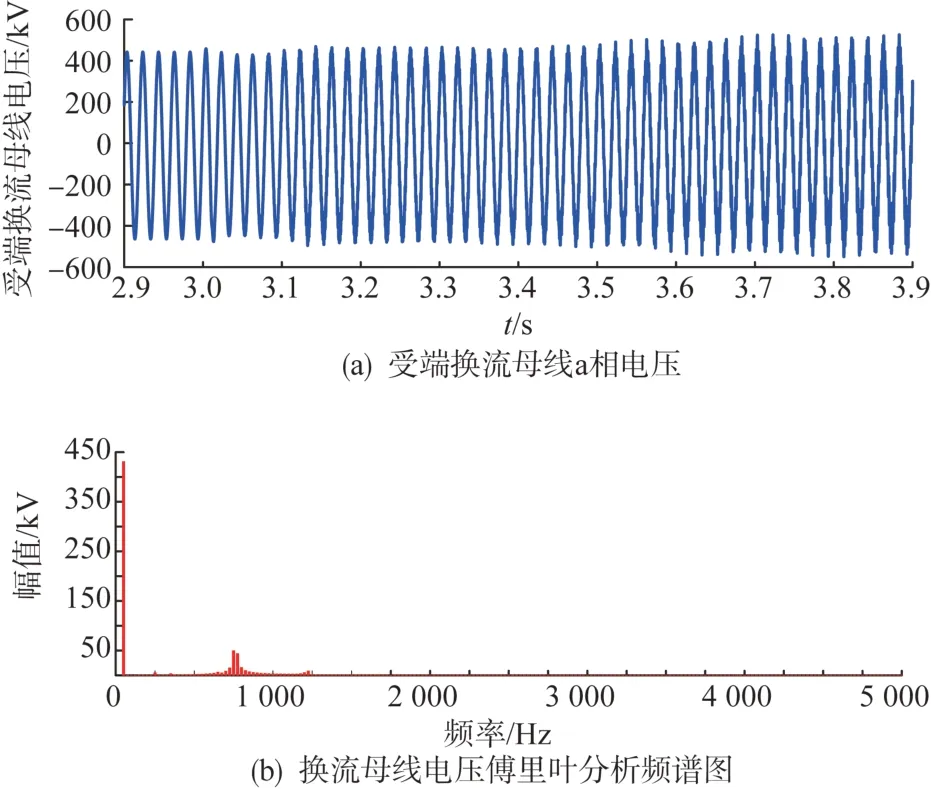
图13 案例1中投入策略2时的仿真结果Fig. 13 Simulation results when implementing strategy 2 in case 1

考虑投入策略3，柔性直流输电系统的仿真结果如图14 所示。图15 为系统检测到的谐振频率及所投入陷波器中心频率曲线图。由图15（a）可知，在3.0s 线路开断后，系统便检测到发生了1 225 Hz的高频谐振，图15（b）也显示在检测到谐振频率后系统投入了中心频率为1 225 Hz 的陷波器进行抑制。但随后系统又检测到发生了1 700 Hz 的高频谐振，导致系统在投入1 225 Hz 和1 700 Hz 的陷波器之间来回切换，最终无法抑制系统的高频谐振现象。该策略只附加了一个陷波器，当系统仅存在一个谐振频率点时，该策略能够自适应地根据系统的运行工况调节陷波器的参数从而抑制高频谐振现象，但当系统存在两个及以上谐振频率点时，该策略的抑制效果则变差甚至无法抑制高频谐振现象。

图14 案例1投入策略3时受端换流母线a相电压Fig. 14 A-phase voltage of the receiving-end commutation bus when implementing strategy 3 in case 1

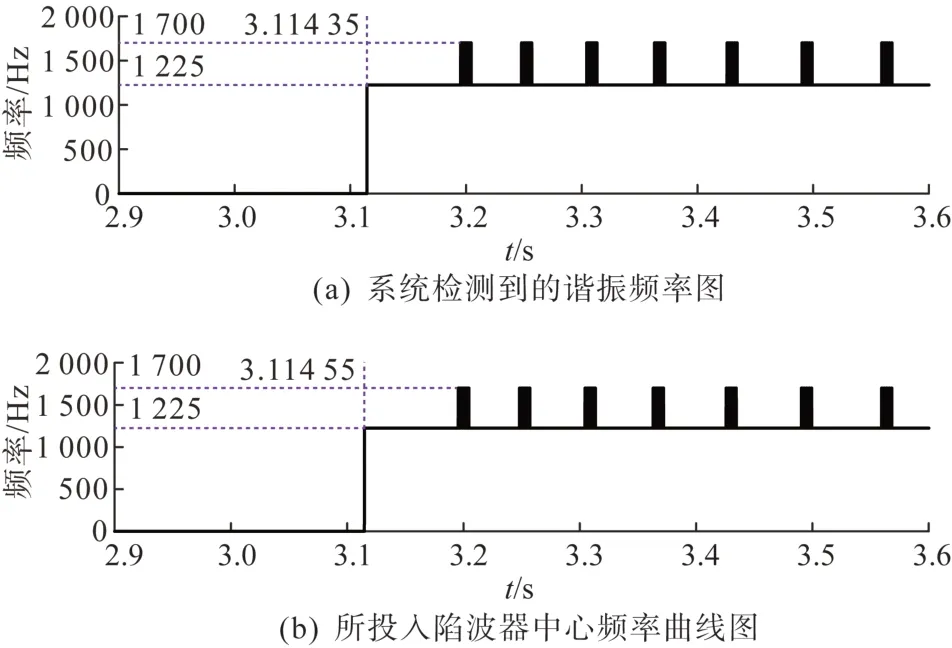
图15 案例1中投入策略3时的仿真结果Fig. 15 Simulation results when implementing strategy 3 in case 1

考虑投入策略4，柔性直流输电系统的仿真结果如图16 所示。图17 为系统检测到的谐振频率及所投入带阻滤波器中心频率曲线图。从图17（a）可知，在3.0 s 线路开断后，系统在0.114 35 s、0.143 s 后分别检测到系统发生了1 225 Hz、1 700Hz 的高频谐振，图17（b）也显示在检测到谐振频率200 μs 后系统分别投入了中心频率为1 175 Hz、1 700 Hz 的带阻滤波器进行抑制。图16 和图17（a）显示在带阻滤波器投入不久后，系统的高频谐振得到了抑制，系统恢复了稳定运行。该策略能够自适应地根据系统的运行工况调节带阻滤波器的数量及参数，可见本文所提的基于自适应带阻滤波器的高频谐振抑制策略能够针对特定谐振频率点以及多谐振频率点的谐振进行抑制，且抑制效果好。

图16 案例1投入策略4时的受端换流母线a相电压瞬时值Fig. 16 Instantaneous values of the a-phase voltage of the receiving-end commutation bus when implementing strategy 4 in case 1

图17 案例1中投入策略4时的仿真结果Fig. 17 Simulation results when implementing strategy 4 in case 1

4.2.3 案例2连续高频谐振仿真结果

本案例的仿真中根据线路开断设置了两个阶段，不同阶段系统中设置不同谐振频率的高频谐振，进一步验证所提策略在系统工况变化下发生高频谐振的谐振频率连续变化情况下抑制策略的有效性。图18 展示了在第二次线路开断后受端换流母线a 相电压的瞬时值，图19 为系统检测到的谐振频率及所投入带阻滤波器中心频率曲线图。

图18 案例2中受端换流母线a相电压瞬时值Fig. 18 Instantaneous values of the a-phase voltage of the receiving-end commutation bus in case 2

图19 案例2中连续高频谐振的仿真结果Fig. 19 Simulation results of continuous high frequency resonances in case 2

从图19 可以看出在系统第一次线路开断时系统检测到发生了1 175 Hz 的高频谐振，并投入了中心频率为1 125 Hz 的带阻滤波器进行抑制。在第二次线路开断后，由于此时系统稳定运行时间已大于设定的稳定运行时间1 s，故所提策略判定此时系统运行方式发生了变化，对所投滤波器参数进行了重置，200 μs 后根据重新检测到的谐振频率计算带阻滤波器的参数，分别投入了中心频率为1 175 Hz和1 700 Hz 的带阻滤波器进行抑制。因此所提抑制策略在检测到新的谐振频率时能够根据实际工况判断系统的运行方式是否发生变化，并调节投入带阻滤波器的数量及参数。综上，在本文所提的抑制策略下，在不同工况下的高频谐振均能在较短的时间内被检测到并成功抑制。

5 结论

本文提出了基于自适应带阻滤波器的高频谐振抑制策略，相较于其他的高频谐振抑制策略，该策略能对系统不同运行方式下的高频谐振进行抑制。通过PSCAD/EMTDC 仿真，验证了所提策略的正确性和有效性，并且得出了以下结论。

1）所提的高频谐振频率检测及分析模块能够较准确地检测出系统的谐振频率，使得所提抑制策略能够准确实时地调整带阻滤波器的数量及参数。

2）所提抑制策略采用带宽较小的带阻滤波器，相比其他类型的滤波器能够保证滤波器的接入仅对谐振点附近频段的阻抗特性产生影响，其它频段的阻抗特性基本保持不变，较大限度地保留了系统的动态特性。

3）经仿真验证，所提基于自适应带阻滤波器的高频谐振抑制策略针对系统状态连续变化导致的高频谐振，能够很好进行识别及抑制。