移动边缘计算中基于贡献度激励的端池化解决方案
阳 柳,章立群,林晓勇
(南京邮电大学 通信与信息工程学院,江苏 南京 210003)
0 引 言
目前基于云计算(Cloud Computing,CC)[1]的研究日益成熟。云计算通过分布式计算技术,即将多台计算机的处理能力组合在一起,形成一个虚拟的计算机,获取超高计算力[2],此过程又称为公共算力池[3-4](Public Computing Pool,PCP)。移动边缘计算(Mobile Edge Computing,MEC)通过将服务器下沉至数据源一侧为用户提供计算和网络等资源,具有更低的时延和能耗,以完成用户的各种业务请求[5-7]。边缘计算通过基站接收各用户的计算任务,通过边缘侧服务器进行处理,以完成用户的请求。
随着技术的发展,终端节点上行链接接入基站,通过云计算和边缘计算完成计算需求。当基站由于外界因素导致基站覆盖范围缩小,基站计算服务器受损,原本处在基站覆盖范围内的节点无法接入,计算任务无法满足。终端设备都存在一定的计算能力,基于算力共享[4]和公共算力池化的理念,通过移动自组织网络(Mobile Ad hoc Network,MANET)进行连接,利用自身可用计算力实现算力共享,此过程即为端池化(Terminal Pooling)。将端池化后的系统计算合力定义为算力池,端池化以算力池作为评判端池化优劣的标准,在基站无法应付大量计算任务的请求时参与计算。
终端节点的数量影响着系统算力池的大小,目前对MANET网络的研究默认节点全都同意接入网络参与通信[8-9],其忽略了节点的自私性。文中通过对节点采取激励策略,提升节点的接入率,增强端计算网络的算力池。由于终端节点自主通信范围受限,通过分簇方式对终端节点进行管理[9-11],并选举簇首节点作为中间节点与基站进行连接,得到算力池最大的分簇方法,不同簇的算力池大小不一,基站可根据算力池下发计算任务。簇首的选举对簇中算力池也存在一定的影响,不同节点具有不同的连接度,作为簇首时组建的簇的特性也不一样。
针对聚簇算法,目前大多数研究都是通过考虑多种因素,通过加权分簇算法选举簇首[11-14]。文献[14]提出一种考虑节点度、节点移动性、节点剩余能量和节点与邻居节点距离和进行加权的方法,并通过带宽确定簇中节点个数,以此提高网络资源效率。该方法虽然考虑了各因素的影响,但忽略了每个因素影响的差异化,即使通过加权因子来平衡各因素的影响,没有从根本上得到最佳的簇首节点。文献[15]通过建立节点剩余能量和位置阈值模型选取簇头及分簇,考虑了节点剩余能量和位置,能够提高能耗效率和对网络生命周期进行分簇,但该方案没有考虑节点计算力对分簇的重要性。文献[16]通过修改K-means算法,根据点与计算的质心的距离进行迭代聚类,直到得到一个稳定的质心,并选取最接近质心的D2D用户作为该组的D2D的簇首,仅以距离作为簇首选举因素,虽然能保证簇的稳定性,却无法保证簇的计算能力。文献[17]通过等角度分簇算法,通过基站到簇首节点的通信半径,得到系统时延最低时的最佳簇首位置,以此选定簇首节点。该文献并没有考虑终端节点直接的通信距离,默认所有节点皆能接入簇中。
综上所述,在已有的分簇方案中,大多都未考虑终端节点通信能力和终端的计算力对簇性能的影响。基于此,该文提出一种基于贡献度激励的端池化(Contribution Emulated Terminal Pooling,CETP)解决方案,重点研究如何提升终端节点的接入率和算力池最大化要求下的簇首选举方式,聚成最佳的簇,通过端池化协助基站快速完成计算任务。
1 系统模型
处于基站覆盖范围内的节点定义为内部节点(Internal Nodes,INs),随着基站覆盖范围缩小,基站覆盖范围外的内部节点定义为外围节点(Peripheral Nodes,PNs),外围节点通过MANET网络与内部节点建立通信连接。设定所有PNs主动加入MANET网络与INs建立通信关系,INs中存在自私节点,不愿与PNs通信。端池化过程中下发的计算任务分为两个阶段:第一阶段为基站通过蜂窝网络将计算任务传递给簇首;第二阶段为簇首通过MANET网络将计算任务传递给簇内节点,通过利用节点的剩余计算力进行端池化,实现计算力共享。
设定小区用户随机分布,外围节点的数量为N,内部节点的数量为M,分别用集合A={1,2,…,n,…,N}和G={1,2,…,m,…,M}表示,INs的通信意愿定义为willingness,用集合W表示。系统模型如图1所示。
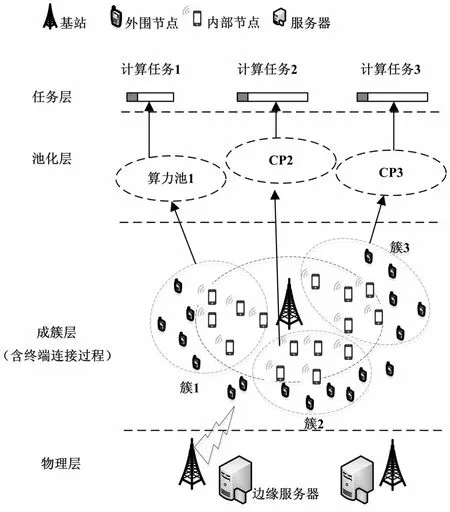
图1 CETP模型
2 端池化
端池化过程计算任务传输的第一阶段,基站将计算任务传递给簇首,所需传输时延定义为tbs,ch,计算过程如公式1所示:
(1)
其中,C为计算任务的大小,Rbs,CH为基站到簇首的传输速率,可用香农公式表示,计算公式如公式2所示:
(2)
其中,B为基站总带宽,K为簇的个数;Pbs为基站的发射功率,dCH为簇首到基站的物理距离;l为路径损耗因子;n0为噪声功率谱密度。
在端池化过程计算任务传输的第二阶段,定义簇首(CH)与簇内节点之间的连接关系为v,当通信条件时,v=1,反之v=0。通信条件表示如公式3所示:
(3)
通信条件(a)表示簇内中IN节点m的通信意愿,当willingness大于通信意愿阈值wthreshold,表示节点愿意加入与簇首建立通信连接;通信条件(b)表示双方节点的物理通信条件,当簇首与簇内节点之间的物理距离小于最大通信范围r时,双方能进行通信。
第二阶段完成计算任务的传输和计算需要的时延为t2,如公式4所示:
(4)
其中,Numk为第k个簇中可通信的簇内节点;fi为簇内节点i的剩余计算力;φ为处理1 bit任务所需的CPU周期;RCH,i为簇首与簇内节点的传输速率,计算过程如公式5所示:
(5)
其中,Bk为第k个簇内节点可用带宽;Pt为簇首的发射功率;dCH,i为簇内节点i与簇首的距离;vCH,i为簇内节点(CH)与簇首的连接关系。
端池化过程完成计算任务C所需花费的总时延包括计算时延和传输时延,计算时延受限于最小节点计算力,传输时延受限于最差节点信道质量,因此总时延为传输时延和计算时延和的最大值。定义总时延为T,计算过程如公式6所示:
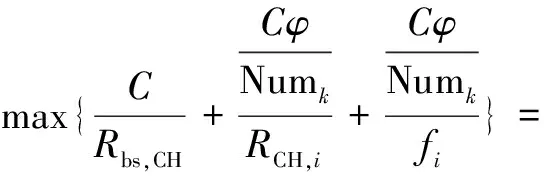
(6)
算力池为一个簇的可用计算力的合力大小,即一个簇综合处理单位计算任务的能力。第k个簇的算力池Fk为所需完成的计算任务大小与所花费时延的比值,计算过程如公式7所示:
(7)
基站与簇首之间的传输时延忽略不计,系统总合力(FF)定义为各簇算力池之和,计算过程如公式8所示:
(8)
基于上述分析,可以得到以系统整体算力池最大为优化目标,对端池化过程的用户进行分簇,得到时延优化下分簇的个数以及簇首接入的节点数。以系统整体算力池最大为优化目标可以化作求以系统时延最小为优化目标,计算过程如公式9所示:

(9)
其中,C1是对簇内接入节点的约束,接入节点不能超过簇中节点个数Sm;C2是对整个系统的簇内接入节点的约束,接入节点不能超过系统内节点个数;C3是簇内节点带宽约束,信道带宽不能超过最大可接入带宽Bmax;C4是簇内的总带宽约束,簇内带宽和不能超过簇中总带宽BCH;C5是系统带宽约束,各簇带宽和不能超过系统总带宽B。
3 激励策略
由公式6可知,接入的Numk影响算力池大小。为了提升INs的连接意愿,提出将贡献度激励INs与外围节点进行连接,以此增加通信的PNs数,从而增加Numk。PNs根据以往作为INs时,成功连接的次数Ks与被申请连接的次数S的比定义为节点的贡献度,表示为Con,如公式10所示:
(10)
系统平均贡献度如公式11所示:
(11)
当PN节点n所申请连接的IN节点m满足通信条件(b)时,不满足条件(a)时,判断该PN节点的贡献度与系统平均贡献度的关系,若大于等于系统平均贡献度,则将该意愿连接节点m的连接意愿进行提升,再判双方是否满足通信条件(a),最后得到INs的连接数以及PNs的接入数。意愿激励公式如下:
(12)
配对策略流程如图2所示。
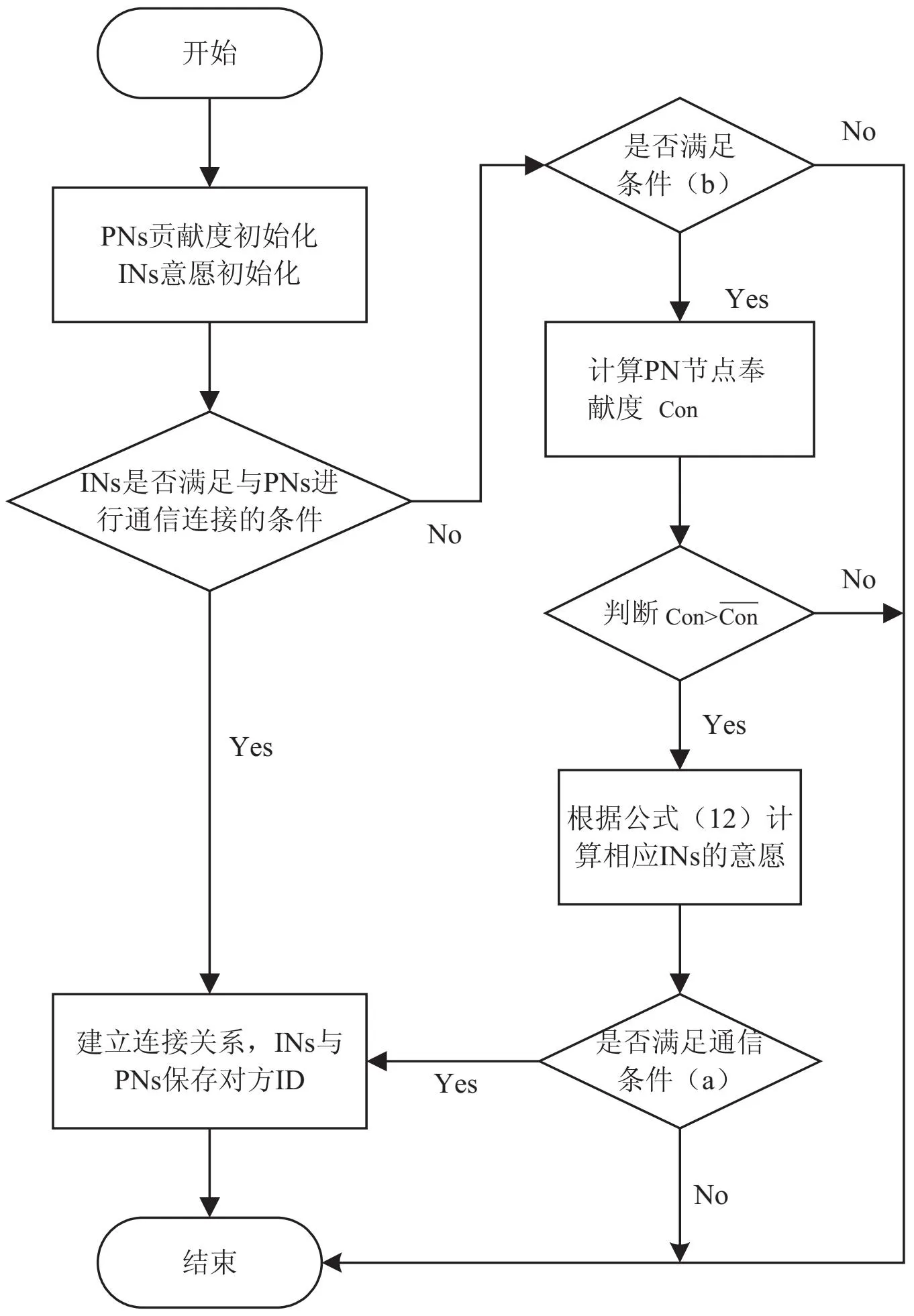
图2 激励策略流程
4 聚簇算法
文中聚簇算法基于k-means算法将系统节点分割为K个簇,簇中包括内部节点和外围节点,内部节点可以根据意愿选择是否加入该簇,通过对比入簇的内部节点作为簇首时簇的算力池大小,选出算力池最大时具体簇的分布。根据公式6和公式7可知,在信道带宽和计算任务相同的情况下,算力池的大小受限于簇中接入数,簇的个数和信道质量,信道质量主要受两点之间的距离影响。
具体算法步骤如下:
输入:B,Bk,Pbs,Pt,C,l,n0,N,M,r,R,Kmax
输出:vij,Numk,K,FF
步骤1:初始化相关参数,得到系统所有节点横坐标X,纵坐标Y;内部节点横坐标X_n和纵坐标Y_n,内部节点意愿willingness;外围节点横坐标X_p和纵坐标Y_p;
步骤2:fork←K_min toK_max do
步骤3: 通过K-means分簇得到初始簇Cluster1;
步骤4:Fori←1 to Numkdo
步骤5:Forj←1 to Numkdo
步骤6:Ifi~=j
步骤7:计算各簇中的节点距离;
步骤8:保存各点满足通信的节点坐标;
步骤9:Endif
步骤10:Endfor
步骤11:Endfor
步骤12:W_k←满足通信条件(a)的簇中内部节点集合,个数为Numk_1;
步骤13:保存与簇中内部节点满足簇中通信条件的节点,连接关系为vij;
步骤14:Fori←1 to Numk_1 do
步骤15:根据公式7计算得到每个内部节点作为簇首的算力池F(i);
步骤16:选举各簇中算力池最大的簇中内部节点作为簇首,保存其F值作为Fk,并保存该情况下的簇内个数Numk;
步骤17:根据公式8得到系统中总算力池;
步骤18:Endfor
步骤19:得到系统合力最大的分簇个数K,系统合力为FF
5 仿真结果及分析
本节详细分析了激励策略下,研究在不同计算任务和小区内节点数的情况下,不同簇首选举算法对系统总时延的影响。为了评估文中算法的性能,将文献[17]的等角度分簇算法作为对比算法1,加权分簇算法作为对比算法2,对比算法2中影响因素为节点计算力、节点连接度以及节点与簇首的距离和。
对比算法1通过等角度分簇,限制了节点根据性能选择簇的权利,不能保证簇中节点加入最佳簇;对比算法2通过考虑不同的影响因素进行加权,在一定程度上保证了所分簇的性能,但权值最佳的簇首所聚的簇不一定是最佳性能簇,因此所分簇的性能存在不稳定性。文中算法是确定所分簇的最佳性来反向选举簇首,并通过端池化来确定系统的计算能力,以最短时延完成计算任务。
该文所采用的仿真参数如表1所示。
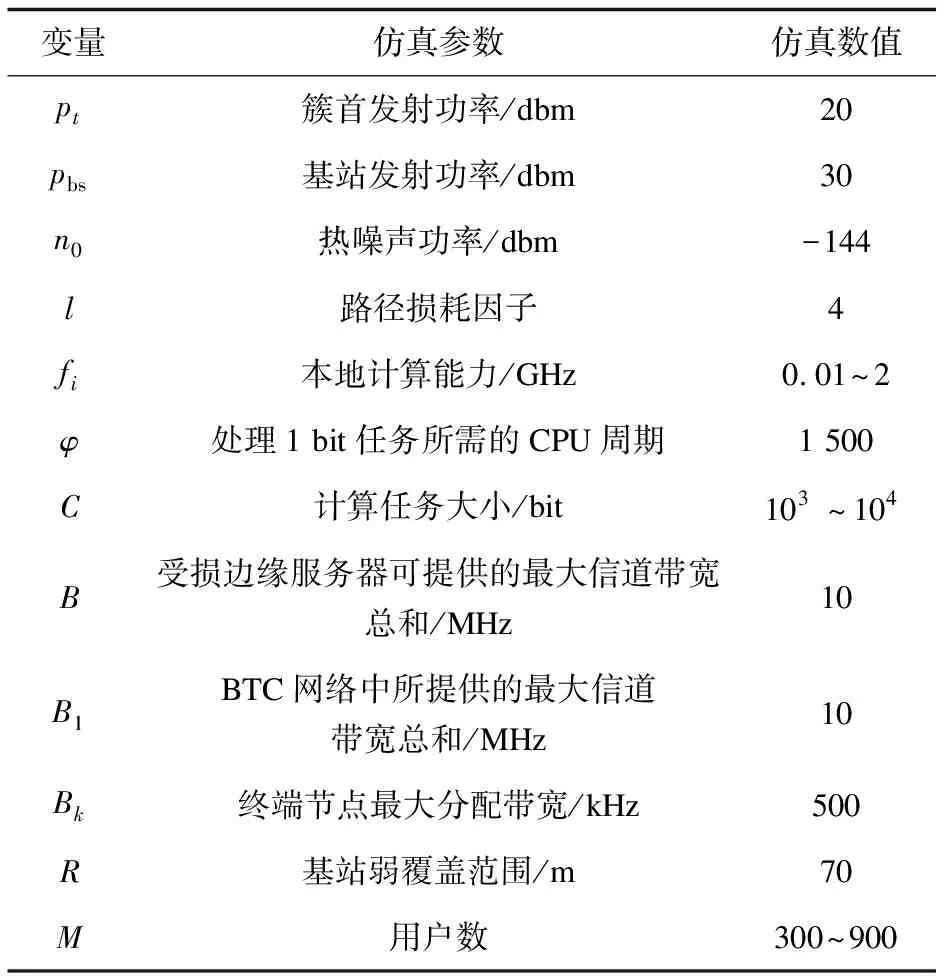
表1 系统仿真参数设置
当用户数为300时,在节点接入的激励策略对比下,不同算法下的用户接入率随计算任务的变化情况如图3所示。由于组网过程存在自私节点,因此理论下的最大接入率无法到达100%。对比算法1是通过等角度的分簇方式,限制了簇首节点选择簇中节点,无法最大限度接入满足通信条件节点,因此接入率最低;对比算法2虽然在一定程度上考虑了簇首节点的接入率,但在加权的影响下,需要综合考虑计算力与节点度的影响程度,无法确定能选出最大接入度的簇首,因此在接入率上低于文中算法;文中算法是基于算力池最大情况下进行聚簇,而簇中节点数影响着算力池的大小,因此文中算法充分考虑节点接入情况,但簇首节点的通信范围受限,无法达到理论最大值。仿真结果表明,相比其他几种算法,文中算法能够得到最大节点接入率。
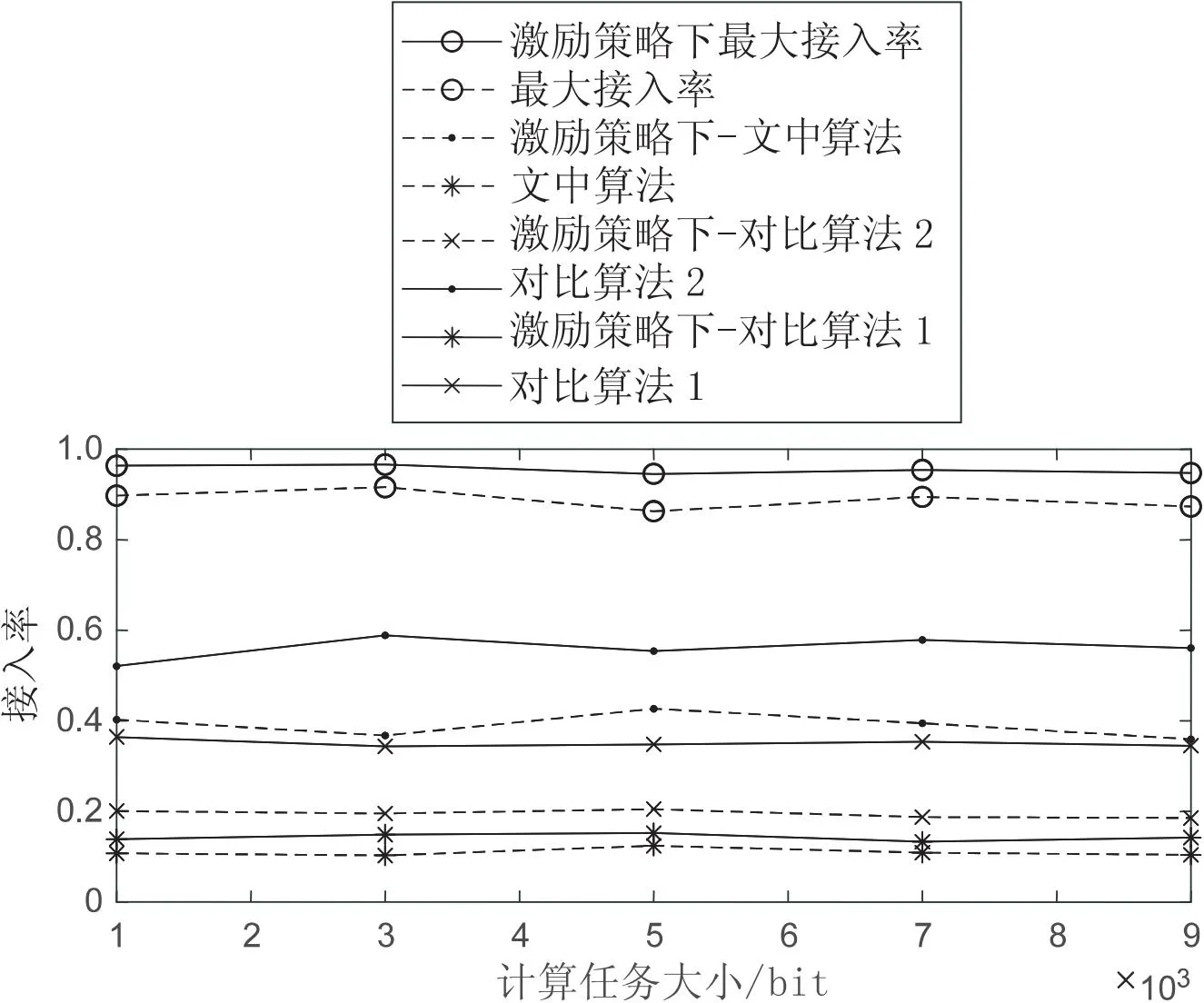
图3 接入率与计算任务的关系
当用户数为300时,在节点接入的激励策略对比下,不同算法下的系统时延随计算任务的变化趋势如图4所示。随着计算任务的增大,各种算法时延都有明显的增加。对比算法1通过等角度分簇,节点随机分布,无法保证每次分簇的稳定性,总体计算力无法保证;对比算法2通过加权多个因素选举簇首,在一定程度上保证了簇的性能,但簇首权值最大不代表整个簇的性能最强。由图3可知,文中算法的节点接入率对比其他两种算法更高,因此系统算力池更大,完成计算任务所花费的时延也更低。仿真结果表明,相比其他几种算法,文中算法能够获得最低的时延。
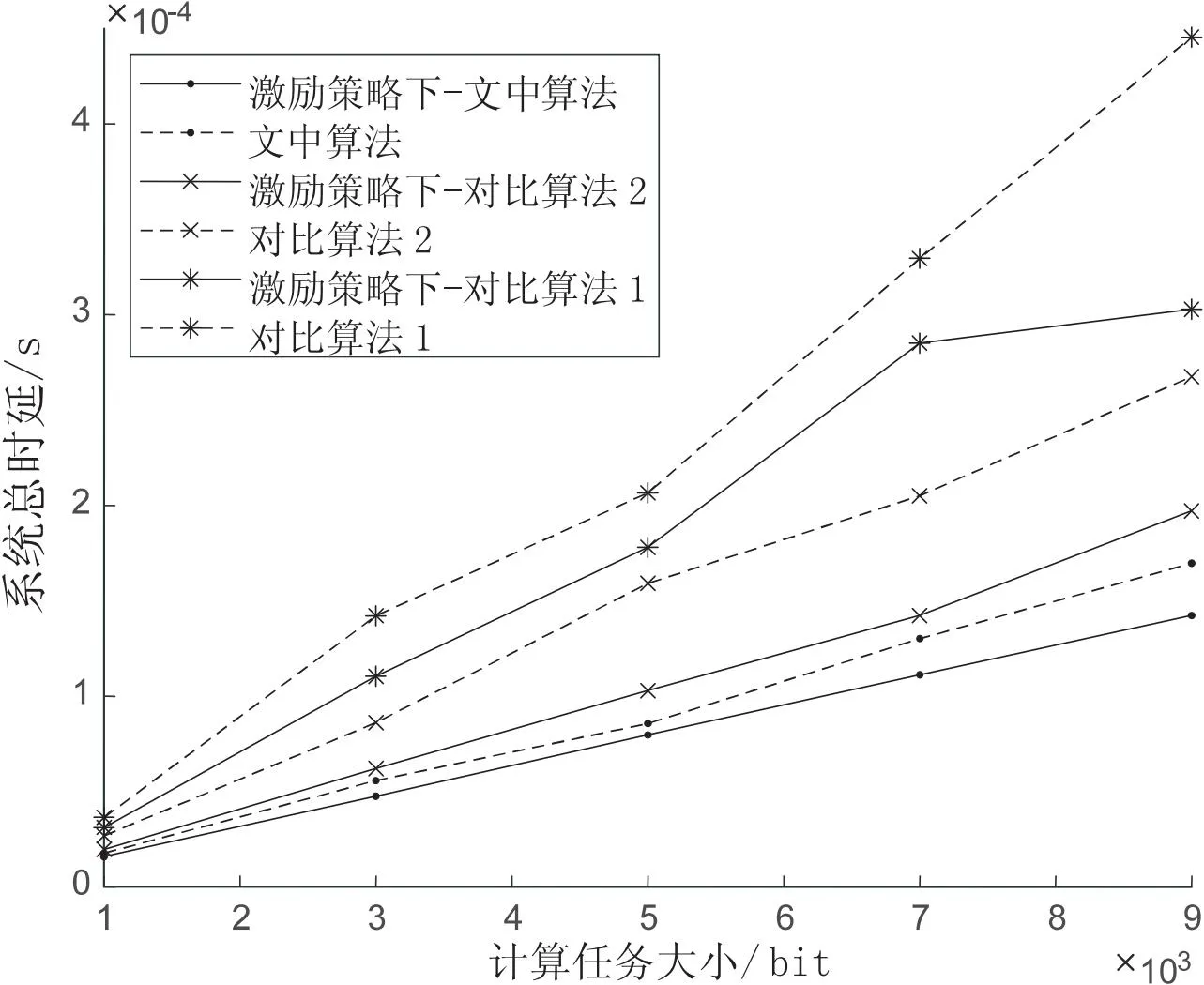
图4 系统总时延与计算任务的关系
当计算任务为103bit时,不同算法下的用户接入率随用户数的变化情况如图5所示。小区覆盖范围不变的情况下,当用户数增加时,单位范围内的用户密度会增加,各算法中的簇首所能接入的用户数也会增加,接入端计算网络的节点越多,用户数的增加并不影响接入率的变化,但数量越多,接入率越稳定。
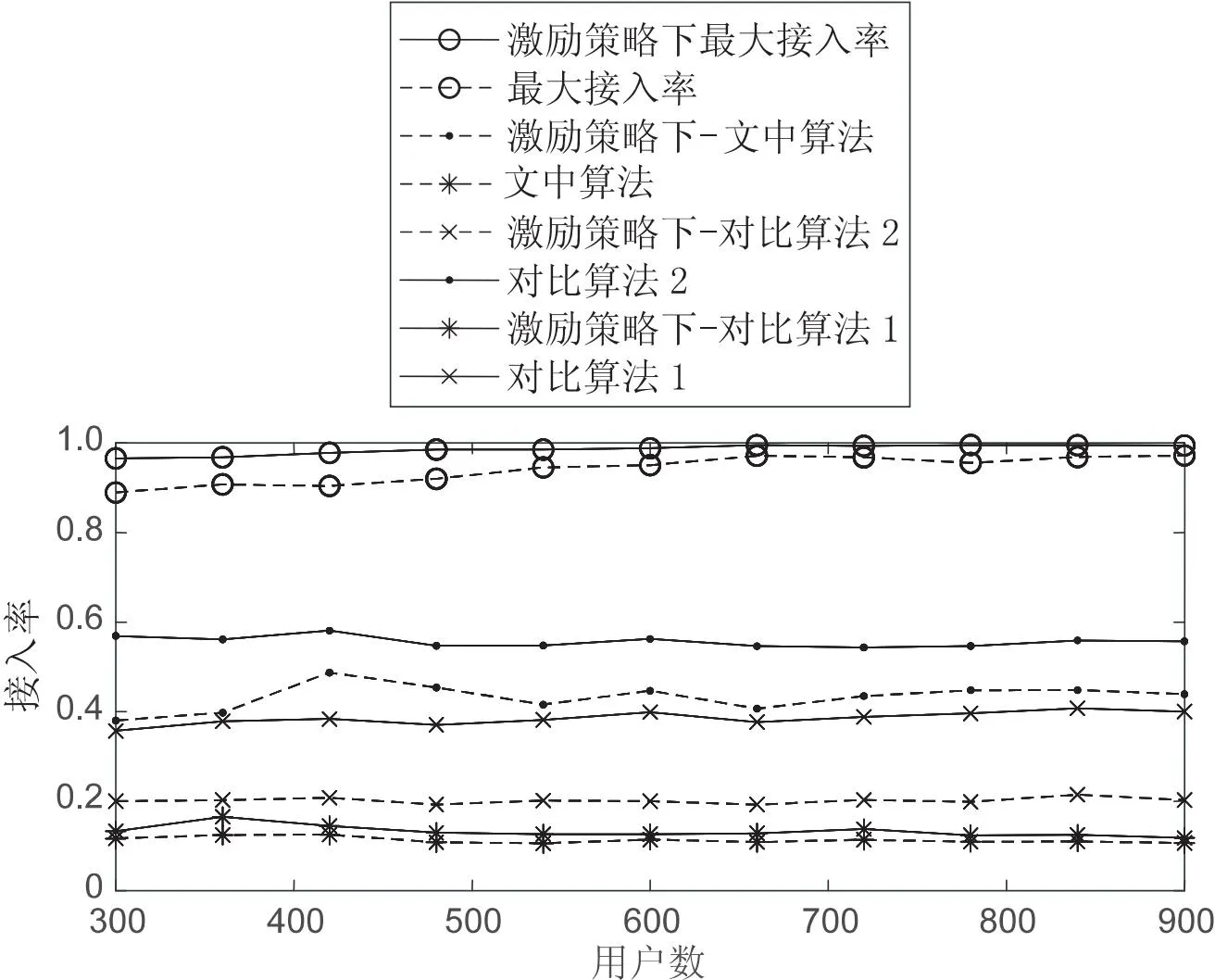
图5 接入率与用户数的关系
当计算任务为103bit时,在节点接入的激励策略对比下,不同算法下的系统时延随用户数的变化趋势如图6所示。小区用户数越多,接入端计算网络的节点数越大,因此各节点所分配的计算任务越小,但随着用户密度增加,算力池受到簇中最差信道和节点最小计算力的约束,最后在用户数为8 000时趋于稳定。仿真结果表明,相比其他几种算法,CETP方案能够获得最低的时延。
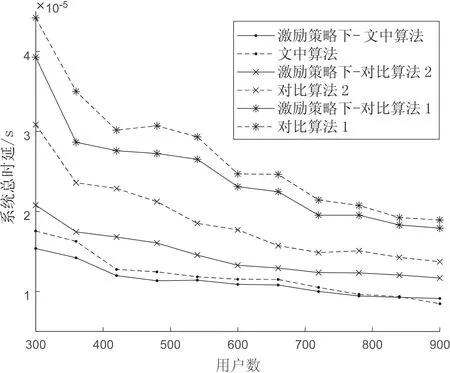
图6 系统总时延与用户数的关系
6 结束语
该文综合了云计算和移动边缘计算技术,在特定的场景下,提出了移动智能终端构建端池化过程的CETP解决方案,并对不同贡献度大小的端节点进行分类,由MANET技术构建通信分簇,根据算力池最大化来选举簇首,通过贡献度激励获取更大的用户接入,最终评估出CETP可获得各种算力池方案结果。仿真结果表明,CETP方案可获得90%以上的接入率,50%以上的参与率,较低的系统时延,以及不同用户数变化下相对稳定的计算时延特性。CETP方案为运营商在雾计算领域中提供了新的算力池化解决思路。

