大跨斜拉桥双层桁架主梁施工状态的阻力系数

李加武，谢泽恩，李嘉煜，李宇 ，赵雪

（长安大学 公路学院，陕西 西安 710064）

随着我国交通基础设施逐渐完善，大跨径桥梁的建设也越来越多，与此同时桥梁更容易受到风的作用发生振动.由于桁架形式多变复杂，使得桥梁主梁阻力系数计算困难.且我国《公路桥梁抗风设计规范》（JTG∕T 3360-01—2018）［1］参考的是英国BS5400规范［2］中采用遮挡系数来计算前后桁架的静风阻力.规范中也仅仅依据桁架的构件形式对单层桁架桥的阻力系数提供了一个简单参考，同时对双层桁架桥还没有全面、详细的规定.研究如何计算双层桁架桥梁的阻力系数，为桥梁的设计提供安全可靠的设计依据，具有一定的工程意义.

在风洞试验方面，李加武等［3-4］通过试验对桁架的静风阻力系数计算提出一个经验公式，发现在不同风攻角作用下，双层主梁的CD值具有显著的变化.陈以荣等［5］发现桁架内设置内墙对钢桁架下侧桥面行人风环境影响较大.翟晓亮等［6］发现最大风速并不一定出现在跨中.Fang 等［7］发现桥梁的扭转可能由下层甲板后面或下方的涡流驱动.Chen 等［8］发现最不利攻角为5°.Li 等［9］发现单一的附加措施不能同时改善原始截面的颤振性能.Bai等［10］发现下中央稳定板使负攻角的升力系数显著降低，从而有利于结构的气动稳定性.Zhu 等［11］通过常态风条件下的截面模型风洞试验研究了上、下中心稳定屏障的气动性能.张瑞林等［12］发现在负攻角状态下，桁架颤振临界风速较高.郭薇薇等［13］测试了不同风攻角作用下的不同车桥系统的三分力.

在仿真模拟计算方面，Tang等［14-16］发现接近桥梁的风场呈现出明显的非均匀特征；发现在大风攻角状态下桁架桥梁横截面呈现钝体特性；发现整个主梁的涡流脱落性能主要受到主梁桁架的影响，并非由于桥面而引起的涡流脱落.Guo 等［17］发现不同高度稳定器对CD值影响较大.邹明伟等［18］通过CFD 数值模拟和风洞试验研究倒梯形桁架主梁断面二维等效模型和气动导纳函数.刘昊苏等［19］认为在低攻角范围内雷诺数对三分力系数的影响几乎可忽略不计.He等［20］证实了导板设置的可行性和可靠性.韩艳等［21］发现宽高比变化对流线型断面摩擦阻力影响显著.

综上所述，现阶段对于桁架桥梁的研究，多针对增加不同措施对结构整体的抗风性能进行提高，而对于双层桁架桥梁阻力系数的研究较少.本文将以某拟建的跨海大桥为例，展开大跨径双层桁架桥风洞试验研究以及数值模拟，初步探索大跨径双层桁架桥阻力系数的变化规律，提出适用于类似双层桁架桥的阻力系数拟合公式，为桥梁的设计提供一个更加合理的参考值.

1 风洞试验

1.1 工程背景

以某跨海大桥为工程背景，该桥是一座全长1 776 m，主跨跨径880 m 的大跨径双层桁架斜拉桥，桁架采用对称布置，主梁横断面呈矩形框架结构，桁架高14 m，宽42.2 m，横梁呈鱼腹式.图1以及图2分别为大桥立面布置图和加劲梁断面图.

图1 桥梁立面布置图（单位：cm）Fig.1 Bridge elevation arrangement（unit：cm）

图2 主梁横断面图（单位：cm）Fig.2 Cross-sectional view of the girder（unit：cm）

1.2 试验概况

试验在长安大学风洞实验室CA-1大气边界层风洞中进行.节段测力模型缩尺比为1∶65，长1.800 m，宽0.649 m，高0.240 m，长宽比为2.77∶1，风洞阻塞率低于5%，满足《桥梁风洞试验指南》［22］要求.试验用测力天平为中国空气动力研究中心研制的杆式5 分量应变天平.节段测力模型要求与实际桥梁的外形相似，且具有足够的刚度.该主梁断面节段模型由测量段和二元端板构成，α 机构和模型相连.试验模型布置如图3所示.

图3 试验设置Fig.3 Experimental set-up

1.3 风轴与体轴下的三分力系数

在沿横桥向的均匀风场中，变化试验攻角α，测出体轴坐标系下节段模型上受到的横向和竖向气动力以及扭转力矩FH、FV和MT.体轴坐标系下三分力系数通过式（1）计算得到.在风轴坐标系下的阻力和升力由式（2）换算得到.

在体轴坐标系下的阻力和升力系数分别为：

式中：qw=ρU2∕2为来流动压，ρ和U分别为空气密度和来流速度；AH和AV为模型对应的参考面积，AH=HL，AV=BL，L、B和H分别为桁架模型的外轮廓的长、宽和高.

风轴坐标系下的阻力和升力为：

式中：α为水平方向与风向夹角.

对应风轴坐标系下，主梁的阻力系数和升力系数通过式（3）计算得到.

为了方便计算，风轴与体轴计算三分力系数时均采取同样外轮廓面积以及桁架特征尺寸.

1.4 试验结果

测力试验结果如图4 所示.试验选取-10°至10°共计21 个工况，主梁阻力系数随风攻角的增大先减小再增大，小攻角（±3°之内）主梁的阻力系数随风攻角变化的增长率普遍在1%以内.大攻角（±3°之外）变化范围内，主梁的阻力系数随风攻角变化的增长率较大，增长率普遍在2%以上，在10°风攻角下主梁的阻力系数相对于在9°风攻角下主梁的阻力系数增长率为6.46%.

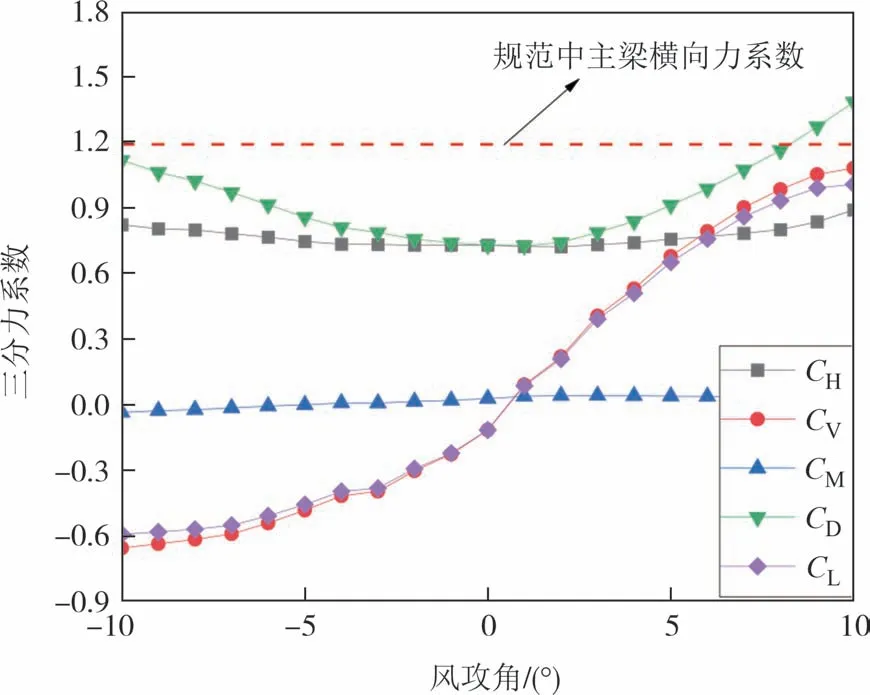
图4 主梁断面静力三分力系数Fig.4 Aerostatic coefficients of the girder

2 数值模拟

2.1 湍流模型

本次模拟采用Shear-Stress Transport（SST）k-ωModel，即剪切应力输送k-ω湍流模型.该模型是在BSL 模型上改进的，并考虑了湍流黏度定义中湍流剪切应力的传输.该湍流模型可以十分有效地使模型内的流体沿流线分离，同时可以对湍流黏性系数进行修正，这样既提高了数值模拟的精度，又有效地减少了计算工作量.

2.2 三维仿真数值模拟

利用ANSYS中SpaceCliam 建立三维仿真节段模型.由于桁架桥的杆件较多，细节尺寸变化较大，使得三维建模有很高的难度，同时网格划分数量以及计算周期会大幅增加.为了方便快捷计算，参考李永乐等［23］对二维桁架模型的简化方法，本文对施工状态下的模型进行如下简化：横梁按照迎风面积大小等效为矩形板；弦杆以及连接件按其迎风面大小使用简化处理；将正交异形板、纵肋和U 形肋简化为一定厚度的平板结构.考虑到计算时间成本以及网格数量问题，选取一个节间作为研究对象.如图5 所示，模型按照图5简化.

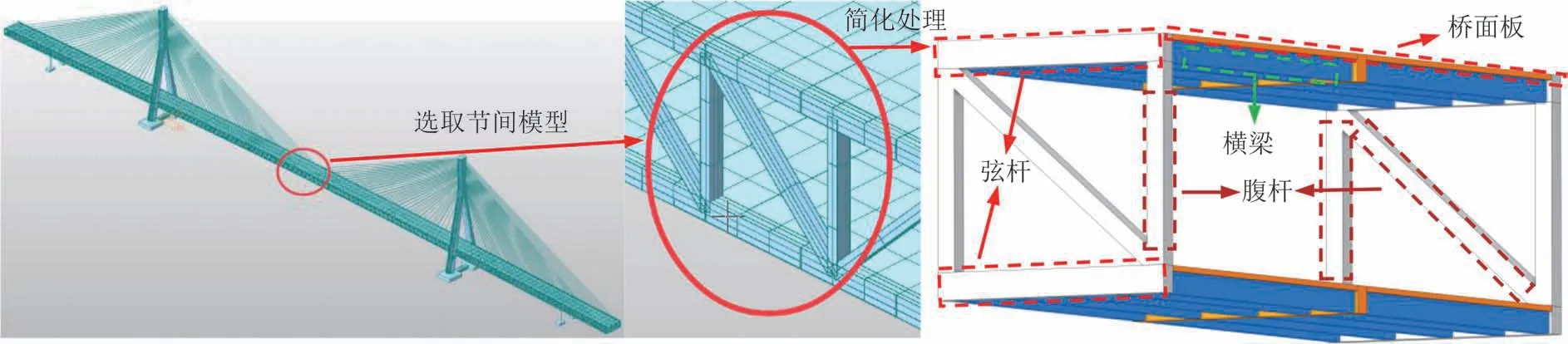
图5 模型简化示意图Fig.5 Simplified schematic of the model

流域尺寸设置如图6 所示.模型距离上下风场边界为5倍标准节段间距的距离，距离入风口为5倍节段间距的距离，距离出风口为20 倍节段间距的距离.在靠近模型处设置边界层，并添加网格加密区，在保证计算精度的前提下，充分平衡计算效率的问题，且满足阻塞率小于5%的要求.

图6 流域尺寸设置Fig.6 Watershed size setting

本次网格划分采用的是poly-hexcore 方法，该方法画出的网格多为六面体网格，相比于四面体网格数量要减小很多，且由于单元按照流动方向有序排列，可以有效地降低分析计算误差.图7 所示为划分网格示意图.图8所示为模型表面网格.

图7 计算域网格示意图Fig.7 Schematic of the calculation domain grid

2.3 网格无关性验证

由于在进行CFD 数值计算模拟中需要考虑网格数量对数值模拟精度的影响，良好的网格既需要有一定的数量，又需要保证较小的计算时间成本，因此，网格数量的选取往往是一个权衡时间成本与精确程度的重要过程.网格无关性验证结果如表1所示.

表1 网格无关性验证Tab.1 Mesh independence verification

根据表1 结果，并考虑计算时间成本，本文选取2.16×106网格的网格划分方式进行后文的研究.本文所涉及所有工况网格质量均在0.15 以上，偏斜度小于0.9，各项参数均满足高质量网格标准.

2.4 工况设置

为了保证模拟结果与试验具有可对比性，采用和试验一样的工况.对施工状态使用正负10°攻角计算，共计21 种工况.为了保证与试验一致，试验风速采用10 m∕s.

2.5 数值模拟与风洞试验结果对比

由规范［1］可知，本次研究桥梁的桁架桥单片桁架实面积比为0.4，由规范表格可知其桁架的阻力系数CH为1.7；该桁架桥间距比为3.071，由规范表格可知桁架遮挡系数为0.7，因此依据规范每片横梁的阻力系数均取为1.19.

通过试验数据与数值模拟数据对比得到图9，从数值上可以看出，在两者主梁的阻力系数对比中大部分数据误差不高于9%.试验数据和数值模拟数据拟合度高，证明可以使用单节间桁架来计算桁架三分力系数，在简化大量网格数量的同时计算效果较好.通过分析数据可以发现在风攻角为0°时，三分力系数均为最小，随着角度的增大而增大.同时也可以很明显地看出在正攻角时，三分力系数都普遍大于负攻角下所得到的三分力系数.

图9 风洞试验与数值模拟结果对比图Fig.9 Comparison of wind tunnel test and numerical simulation results

通过对比规范中规定的限值与风洞试验以及数值模拟结果，可以看出规范中的主梁阻力系数远远大于试验以及模拟的主梁阻力系数.依照规范，风攻角通常选取为±5°，在此风攻角条件下，规范与试验以及模拟的结果相比，最大仍有50%的富裕度，最小也有25%的富裕度.因此，如果大跨径双层桁架主梁阻力系数按照规范取值，会出现取值偏大的情况，从而使得桥梁设计出现一定的资源浪费现象.

根据规范［1］可知，由于桁架的复杂性，阻力系数一般由风洞静气动力试验给出，取值为±3°之内的最大值.由本文试验与数值模拟计算得到该双层桁架桥主梁的阻力系数分别为0.731 与0.708.对上述数据进行拟合得到公式（4）.

式中：α为风攻角，（°）.

3 节间特征尺寸对主梁阻力系数的影响

3.1 实面积比

由于桁架桥梁不同于其他形式桥梁，比如箱梁在迎风面的阻风面积为其在迎风面的最大投影面积，而桁架桥梁由于其桁架的空间结构形式影响，其在迎风面的对应轮廓面积要远远大于实际阻风面积.因此在规范中提出了实面积比的概念，即实际阻风面积与桁架轮廓面积之比.

3.2 工况设置

由于实面积比与桁架布置有关，为研究实面积比对桁架主梁阻力系数的影响，以节间高度与节间宽度为变量，并以此来探究主梁阻力系数的变化规律.针对节间宽度，通过改变节间横梁个数，来控制实面积比的变化.针对节间高度，本文以原始断面高度为基础，分别设置不同倍数的节间高度，并以此控制实面积比的变化.为保证模拟结果具有一定可靠度，采取和原始模拟模型相同的网格划分设置以及湍流模型，工况如表2所示.

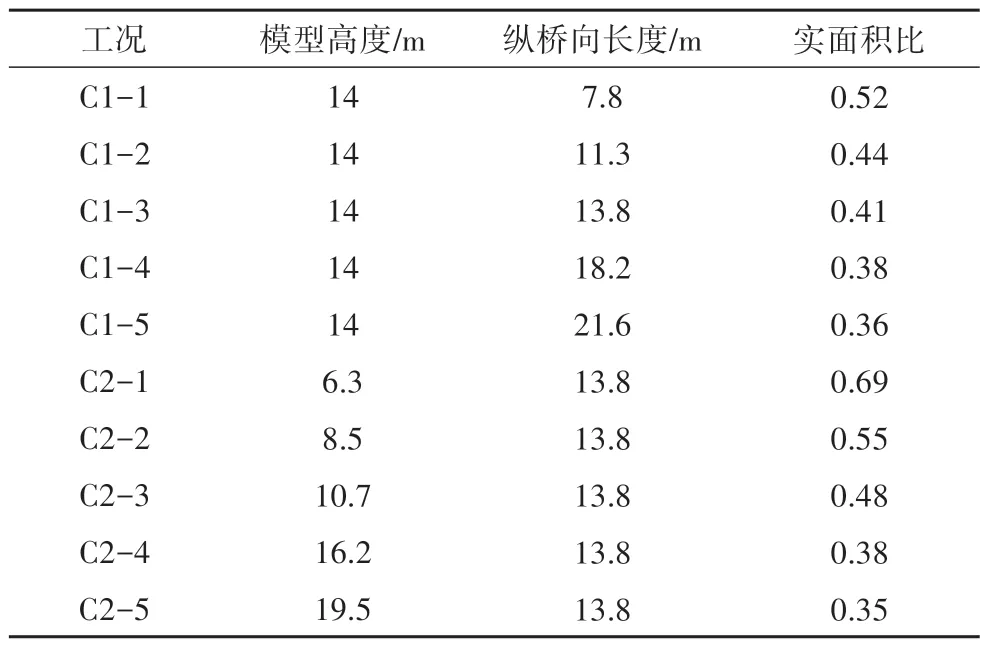
表2 双层桁架桥梁不同实面积比工况表Tab.2 Working condition table of double-deck truss bridge with different real area ratio

3.3 数值模拟结果

对上述工况采取相同的设置条件，分别得出对应三分力系数.针对节间宽度变化对主梁的阻力系数模拟结果如图10 所示.一般来说，实面积比越大，桁架桥梁的主梁阻力系数也越大.但通过本次数值模拟的结果可以看出，实面积比对主梁阻力系数的影响并不是呈线性关系，因为节间宽度变化对主梁的阻力系数的影响呈先减小后增大的趋势.

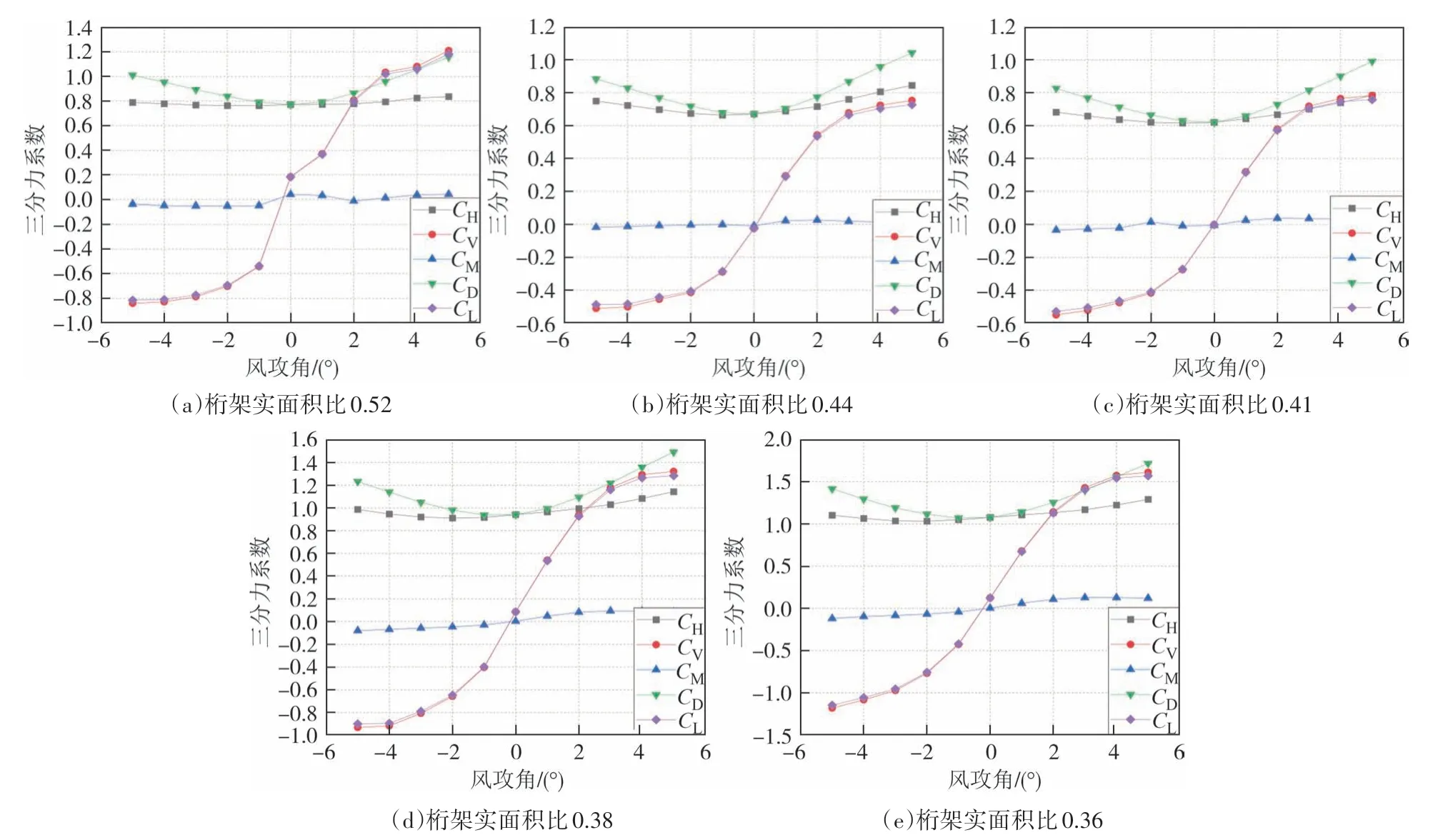
图10 不同节间宽度的双层桁架桥梁三分力系数Fig.10 Aerostatic coefficients of double-deck truss bridges with different internode widths

与此同时，通过改变节间高度来研究因高度变化导致实面积比对双层桁架桥梁主梁的阻力系数的影响，结果如图11 所示.在0°风攻角作用下主梁阻力系数随着桁架实面积比的减小而减小.减小的幅值由0.864 降到0.566，变化幅度仅约为0.3.在5°风攻角作用下，可以明显地看到，主梁的阻力系数CH随着桁架实面积比的减小而减小，由1.08 降至0.709，变化幅值与0°风攻角时保持一致.在风轴坐标系下，可以很明显地看出，双层桁架桥梁主梁的阻力系数CD有大幅度变化，由1.48 降至0.87.在节间高度的影响下实面积比在0.33～0.69 之间双层桁架桥梁的阻力系数随着实面积比的减小而减小.

图11 不同节间高度的双层桁架桥梁三分力系数Fig.11 Aerostatic coefficients of double-deck truss bridges with different internode heights

此时发现双层桁架桥梁主梁的阻力系数随着高度改变导致的实面积比的减小而逐渐减小.与规范中呈现的趋势基本相似，但减小幅度远远小于规范中下降幅度，且在数值大小上要远远大于数值模拟的结果.

3.4 经验公式拟合

一般地，实面积比越大，桁架桥梁的主梁阻力系数会越大，但经过数值模拟得到的结果显示：由于桁架的特征宽度与特征高度对主梁的阻力系数影响趋势也不同，所以使用桁架的实面积比来进行计算是不合理的.

由于在规范中一般考虑±3°的风攻角，特殊情况需要考虑±5°的风攻角，由此，可以采用5°的风攻角的三分力系数作为双层桁架桥梁的三分力系数进行计算.本文提出采用不同纵高比来表达主梁的阻力系数，纵高比即为双层桁架桥的纵桥向中一个节间长度与桁架高度的比值，得到如下公式：

式中：z为纵高比.

4 桁架间距对主梁阻力系数的影响

4.1 桁架间距

如图12 所示，为了保障桥梁的整体结构稳定，有时桥梁设计中会采用三片桁架结构，即图中所圈示的三片桁架.由于每片桁架间也可能产生相互影响，尤其当多片桁架距离较近时，需要考虑前后桁架之间的影响.

图12 三片桁架示意图Fig.12 Diagram of the three-bay truss

4.2 工况设置

为探究桁架间距对双层桁架主梁的阻力系数影响，本文采用改变原桁架的间距进行模拟，采取和原始模拟模型相同的网格划分设置以及湍流模型.工况如表3所示.

表3 桁架间距研究工况表Tab.3 Working condition table for study of truss spacing

4.3 两片桁架不同间距对主梁阻力系数的影响

两片桁架数值模拟结果如图13 所示，可以很明显地看出，在0°风攻角作用下，不同桁架间距的两片双层桁架桥梁的主梁阻力系数呈现先减小后增大的趋势.而在+5°风攻角作用下，两片双层桁架桥梁的主梁阻力系数呈现依次增长的趋势，且随着间距的增加其增长幅度逐渐减小.

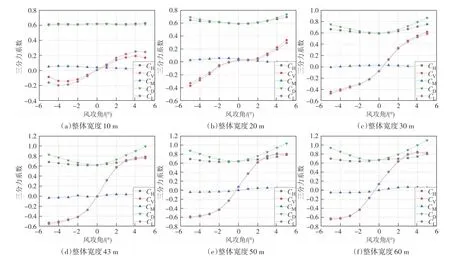
图13 不同桁架间距的两片双层桁架桥梁三分力系数Fig.13 Aerostatic coefficients of two double-deck truss bridges with different truss spacing

4.4 三片桁架不同间距对主梁阻力系数的影响

三片桁架的数值模拟结果如图14 所示.仅从趋势上看，在整体宽度一致的前提下，两片和三片桁架桥梁的数值模拟趋势几乎一样.但在数值上三片桁架桥梁的主梁阻力系数略高于两片桁架桥梁的主梁阻力系数.当最远两片桁架间距与桁架高度比值大于3 时，可以清楚地看到，三片桁架的主梁阻力系数随着间距的增大，其相较于两片桁架的主梁阻力系数的增长速率逐渐增加.

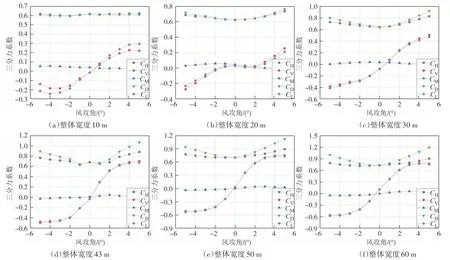
图14 不同桁架间距的三片双层桁架桥梁三分力系数Fig.14 Aerostatic coefficients of three double-deck truss bridges with different truss spacing

5 结论

通过对某拟建大跨径双层桁架桥梁分别进行风洞测力试验和三维数值模拟，初步研究了桁架布置形式对阻力系数的影响，主要得到以下结论：

1）按照迎风面面积大小对桁架主梁进行简化，并选取一个节间作为计算模型，从桁架梁的气动参数结果可以判断，此做法简便易行，具有一定的实际应用价值.

2）双层桁架桥梁的横桥向阻力系数在不同风攻角下取值近似于二次函数.并采用数值拟合的方法得到一个关于风攻角变化的双层桁架桥梁主梁的阻力系数拟合公式，且正攻角下风对双层桁架桥梁的阻力系数影响更大.

3）计算桁架节间的宽高比，并据此拟合双层桁架桥梁在不同风攻角下的主梁阻力系数随纵高比变化的经验公式，可为同类型双层桁架桥梁设计提供一个合理、经济的主梁阻力系数计算参考值.

4）当双层桁架桥梁的主梁宽度与桁架高度之比小于3 时，中间是否增设一片桁架对主梁的阻力系数几乎没有影响；但当双层桁架桥梁的主梁宽度与桁架高度之比大于3 时，中间加设一片桁架对主梁的阻力系数影响较大，但不会改变主梁阻力系数的变化趋势.