基于Hydrolight 模型的太湖SDGSAT-1卫星悬浮物浓度反演研究

王雅萍 胡雪可 , 李家国 姜晟 陈兴峰 赵利民 陈洪真

（1 河南理工大学测绘与国土信息工程学院，焦作 454000）

（2 中国科学院空天信息创新研究院，北京 100094）

（3 江苏省环境监测中心，南京 210019）

0 引言

水体中的悬浮物是指不溶于水的无机物、有机物、泥沙、微生物和黏土等悬浮在水中的固体物质，陆地养分会附着在悬浮颗粒表面导致水体污染现象发生[1]，因此监测水中悬浮物浓度是反映水质现状及发展趋势的重要手段。遥感技术能够大尺度、周期性、快速同步获取水体信息[2]，可以有效监测水中的悬浮物，在当前内陆水体水质监测中的应用日益广泛[3-4]。可持续发展科学卫星1 号（SDGSAT-1），是全球首颗专门服务《联合国2030 年可持续发展议程》的科学卫星[5-6]，由中国科学院“地球大数据科学工程”先导专项研制。该卫星配备的多光谱成像仪（Multispectral Imager for Inshore，MII）在探测谱段、空间分辨率和幅宽上的设置使其在水环境探测方面具有独特优势。SDGSAT-1 MII 传感器共设置7 个光谱通道[7]，空间分辨率为10 m，幅宽为300 km，除了蓝、绿、红、近红外通道外还设置了深蓝通道和红边通道，可以更好地辨识水体浑浊程度，更有针对性地探测内陆水体中的悬浮物浓度。

现有的反演悬浮物浓度的方法主要包括分析法、经验和半经验法。其中分析法主要基于生物光学原理来反演悬浮物浓度，例如：文献[8]利用分析模型反演了巢湖的总悬浮物浓度，文献[9]利用两个近红外波段反射率反演了悬浮物浓度。经验法则是采用一定的数学统计方法来进行悬浮物浓度的反演，例如：文献[10]结合实测数据和Landsat 影像建立了基于红色波段的经验模型对青海湖开展了近35 年的悬浮物浓度时空变化分析，文献[11]开发了基于MODIS 的波段比值算法用于长江中下游湖泊水库的悬浮物长期变化研究。半经验法主要基于水体表观特征与悬浮物的关系来构建悬浮物浓度反演模型，例如：文献[12]利用光谱吸收特征参数开发了适用于GOCI 的悬浮物反演算法，文献[13]提出了一种基于多波长的半分析推导算法用于估计清澈至极浑浊水体中的悬浮物浓度。当前应用较为广泛的是经验模型或半经验模型[14-15]，然而水体反射率信号受水体中不同组分吸收特性和散射特性[16]的影响，悬浮物、叶绿素a和有色可溶性有机物（Colored Dissolved Organic Matter，CDOM）是通常所称的“水色三要素”，现有的悬浮物浓度反演研究很少考虑到叶绿素a、CDOM 的影响，水中叶绿素a、CDOM 对水体的光学贡献不能忽略[17-18]，在悬浮物浓度反演过程中，需要避免叶绿素a 浓度和CDOM 浓度信息的干扰。

Hydrolight 辐射传输模型模拟的水体反射率可以作为水体辐射传输方程的直接解[19]，基于模拟光谱与水体不同组分浓度之间的相关关系，可以探索不同波段叶绿素a、CDOM 的影响贡献，有助于推导反演过程[20]。太湖作为典型的内陆富营养化浅水湖泊[21]，湖水常年浑浊，悬浮物特征显著。综上考虑，本文以太湖为研究区，基于Hydrolight 辐射传输模型和SDGSAT-1 MII 谱段的遥感数据来模拟反射率与悬浮物、叶绿素a、CDOM 的相关性特征，以探明对悬浮物敏感而对叶绿素a 和CDOM 相关性较弱的反演因子，从而构建太湖地区适用于SDGSAT-1 卫星的具有理论基础的悬浮物浓度反演模型，发挥SDGSAT-1卫星在水质参数反演方面的应用价值，为改善太湖水质、治理水环境提供有价值的技术参考。

1 研究区与数据

1.1 研究区概况

太 湖 位 于 长 江 三 角 洲 地 区（30°55′40"N~31°32′58"N，119°52′32"E~120°36′10"E），水 域 面 积 为2 338.1 km2，是中国第三大淡水湖。太湖最大水深不超过3 m[22]，属于浅水型湖泊，在风浪作用下容易导致泥沙再悬浮，增加水体的悬浮物浓度，引起湖中其他物质的流动和释放，促使湖中藻类大量繁殖，加剧湖泊富营养化，水质恶化和环境问题比较严重。悬浮物与太湖地区的水环境质量和经济发展密切相关，监测太湖水体中的悬浮物浓度具有重要意义。

1.2 遥感数据

SDGSAT-1 卫星MII 传感器光谱响应函数如图1 所示，该传感器共包含7 个通道，在蓝、绿、红、近红外这4 个通道的基础上增加了深蓝1、深蓝2 和红边等3 个通道，这样的设置有助于探测浑浊水体水质的变化。研究所用遥感数据为2022 年5月4 日SDGSAT-1 MII L4 级别的太湖影像数据，在使用数据前需要对其进行辐射定标、大气校正、水体提取等预处理工作。其中辐射定标的目的是将DN 值转换为辐亮度；大气校正首先在ENVI 遥感影像处理平台中构建出SDGSAT-1 影像的光谱响应曲线文件，然后利用ENVI 中的FLAASH 模块得到校正后的反射率影像；最后利用水体指数对太湖水域进行掩膜提取。

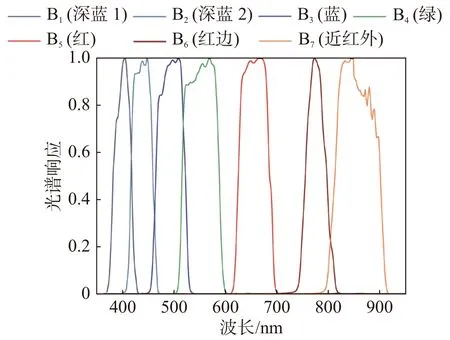
图1 SDGSAT-1 MII 多光谱传感器光谱响应函数Fig.1 Spectral response function of SDGSAT-1 MII multispectral sensor

1.3 实测数据

实测数据分为数据集1 和数据集2，其中数据集1 为2013 年8 月和2015 年10 月对太湖野外采样获取的2 期数据，包括采集的水体光谱数据、水质参数浓度数据和固有光学数据，有效样点数据54 个；数据集2 为2022 年5 月4 日采集太湖水样获得的悬浮物浓度数据，有效样点18 个，选取该系列实测数据是为了验证悬浮物浓度反演模型在SDGSAT-1 卫星遥感影像上的应用效果。两个数据集采样点分布如图2 所示。

图2 实测样点分布Fig.2 Measured sample point distribution

水面光谱测量的目的是获取水体遥感反射率Rrs(λ)，采用ASD 光谱仪通过水面以上测量法[23]进行，测量时的观测方位角为135°，观测天顶角为40°。水体反射率Rrs(λ)计算公式为

式中Rrs(λ)为水体反射率；λ为水体反射率的波长；Lt(λ)、Ls(λ)、Lp(λ)分别为光谱仪面向水体、天空和标准灰板测得的信号值；rs为气水界面对天空光的反射率，平静水面为0.022，在5 m/s 风速情况下可取0.025，在10 m/s 风速条件下取0.026~0.028；ρp(λ)为实验室内标定的灰板反射率。

叶绿素a 浓度参考国家标准（SL 88—2012）采用分光光度计法测量，测定的数值范围在0.27~133 mg/m3；悬浮物浓度参考国家标准（GB11901—89）采用煅烧称重法测定，测定的数值范围在15~145 g/m3。叶绿素a 和悬浮物的光谱吸收利用直径为25 mm 的GF/F 玻璃纤维过滤器过滤水样后使用紫外/可见双光束积分球分光光度计测量，具体操作参考文献[24]中的方法进行。悬浮物和叶绿素a 的散射特性使用文献[25]中的方法测量。有色可溶性有机物（CDOM）的浓度用其在440 nm 处的吸收系数表示，采用紫外/可见光分光光度计测量吸光度，然后将吸光度转换为吸收系数[26]，测定的CDOM 吸收系数（λ=440 nm）数值范围在0.22~1.33 m–1。

2 研究方法

2.1 Hydrolight 模拟

Hydrolight 模型以水体辐射传输理论为依据，模拟太阳光经过水、大气时被吸收、散射的情况[27]。太湖水体组分构成符合纯水、叶绿素a、CDOM 和悬浮物四组分模型，因此选用CASE 2 IOPS 模式对太湖水体反射率Rrs进行模拟。在该模式下，利用水体各组分的固有光学参数和环境变量作为输入模拟遥感反射率。

外界环境条件中的水面风速设为5 m/s，太阳高度角设为60°，水体的折射指数设为1.34；天空辐射传输模型选用RADTRAN 模型，天气状况参数采用模型默认值。

水体各组分吸收和散射部分的输入参数可参照式（2）~（5）和54 组实测数据设定，水体反射率Rrs和水体总吸收系数a(λ) 、 水体总后向散射系数bb(λ)之间的关系可表示为

式中f和Q为太阳天顶角的函数，均受太阳高度角、观测角度的影响；t为气水界面的透射系数，通常取0.98；n为水体折射指数，通常取1.34。

水体总吸收系数a(λ) 和 水体总后向散射系数bb(λ)可以认为是水体不同组分贡献的线性叠加，每个组分的固有光学量可以表示为单位固有光学量和相关成分浓度的乘积[28]。其中a(λ)由纯水、叶绿素a、悬浮物、CDOM 等4 部分吸收贡献组成，水体后向散射bb(λ)由纯水、叶绿素a、悬浮物等3 部分贡献的后向散射组成，计算公式分别为：

式中aw(λ)和bw(λ) 分别为波长λ处纯水的吸收系数和散射系数，其中aw(λ)采用文献[29]中的数值，纯水的散射系数采用文献[30]中模型的数值，如图3（a）所示；w为纯水的后向散射比例，取值为0.5；(λ)和b∗chla(λ)分别为波长λ处叶绿素a 的比吸收系数和比散射系数，两者的输入值来源于图3（b）所示的54 组样点相关数据的平均值；ρchla为叶绿素a 浓度，由测得的54 组样点的浓度数据计算；chla为叶绿素a 的后向散射比例，参照文献[31]中的经验数值设置为0.005；a*tsm(λ)和b*tsm(λ)分别为波长λ处悬浮物的比吸收系数和比散射系数，以图3（c）中计算的54 组样点相关数据的平均值作为两者的输入；ρtsm为悬浮物浓度，根据测量的54 组样点的浓度数据求得；tsm为悬浮物的后向散射比例，参照文献[31]中的经验数值设置为0.028；acdom(440)为波长440 nm 处CDOM 的吸收系数，表示CDOM 浓度，由测量的54 组样点的数据算得；(λ) 为 波长λ处CDOM 的比吸收系数，其与acdom(440)之间符合指数衰减模型，具体关系为

图3 Hydrolight 模型中设定的固有光学参数Fig.3 Intrinsic optical parameters set in the Hydrolight model

式中Sg为CDOM 吸收光谱的指数函数斜率。本文计算的54 组太湖CDOM 吸收光谱Sg平均值约为0.015。

2.2 反射率与三要素相关性分析

由于模拟光谱数据是连续的分布，需要利用SDGSAT-1 MII 传感器的光谱响应函数将模拟光谱数据进行卷积，转换为卫星对应通道的反射率，计算方法如下：

式中R(Bi) 为 SDGSAT-1 第i通道的反射率；Rrs(λ) 为间隔为1 nm 的模拟光谱反射率； λ1、 λ2为卫星第i通道两端的波长；g(λ)为SDGSAT-1 MII 传感器的光谱响应函数。Hydrolight 模拟的光谱数据波长为400~800 nm，其波长范围覆盖SDGSAT-1 MII 第2~6 通道的反射率。

文献[32]的研究表明，对反射率进行比值、差值处理后再应用到反演模型中能够提高反演效果。因此，本文将模拟反射率转换为SDGSAT-1 MII 通道反射率后，再对反射率继续进行比值、差值处理，分别得到比值反射率组合R′(Bi/Bj) 和 差值反射率组合R′(Bi-Bj)，即：

式中R(Bj)表示模拟的SDGSAT-1 第j通道的反射率。

然后，对不同反射率组合与叶绿素a、悬浮物、CDOM 三种要素浓度进行相关性分析，相关系数r的计算公式为

式中m为样本序号；z为样本量总个数；x为从不同反射率组合中选取的变量的取值；y为从叶绿素a浓度、悬浮物浓度、CDOM 浓度中选取的变量的取值；、分别是变量x、y的均值。

相关性分析还包括显著性双尾检验，目的是检验变量之间相关关系是否显著，相关系数r和统计量t的关系可表示为

根据双尾检验中的显著性p值范围，判断变量间的相关性是否显著以及显著性级别，p值与t之间存在的关系为

当p>0.05 时，表示不存在显著相关关系；当p<0.01 时，表示在0.01 级别（双尾）的相关性显著；当p<0.05 时，表示在0.05 级别（双尾）的相关性显著。

2.3 反演模型构建

为避免叶绿素a、CDOM 等光学因子对悬浮物浓度反演的影响，研究选择与悬浮物呈显著强相关，同时与叶绿素a、CDOM 相关性较弱的反射率组合为反演因子，建立悬浮物浓度反演模型。以反演因子为自变量（包括比值反射率组合或差值反射率组合），悬浮物浓度作为因变量分别构建指数模型、线性模型、对数模型、二次模型与幂模型等5 种模型形式。

2.4 反演模型验证

利用均方根误差ERMS、平均绝对百分比误差EMAP、归一化均方根误差ENRMS三个统计指标对模型进行评价，计算公式分别为：

其中，y′k表示第k个样点的悬浮物反演值；h为样点数；yk表示第k个样点的悬浮物实测值；S为计算标准差的函数。

3 研究结果

3.1 Hydrolight 反射率模拟结果

模拟波段范围选择400~800 nm，模拟间隔为1 nm，通过输入54 个样点的叶绿素a、悬浮物、CDOM 吸收系数（λ=440 nm）的实测数据，以及设定的各组分吸收和散射部分的固有光学数据，得到54 组模拟光谱，模拟反射率和实测反射率数值较为接近，结果如图4 所示，54 组模拟光谱与实测光谱拟合后的决定系数R2为0.906，两者存在较为显著的线性关系。进一步统计每个样点的实测光谱与模拟光谱的相关系数，图5 为54 组实测样点的叶绿素a 浓度、悬浮物浓度和CDOM 吸收系数（λ=440 nm）数据及其模拟光谱和实测光谱的相关系数，结果表明所有样点的模拟光谱与实测光谱的相关系数均在0.93 以上，其中相关系数在0.95 以上的样点占比83.3%，可见模拟反射率能够作为相关性理论分析的基础数据。

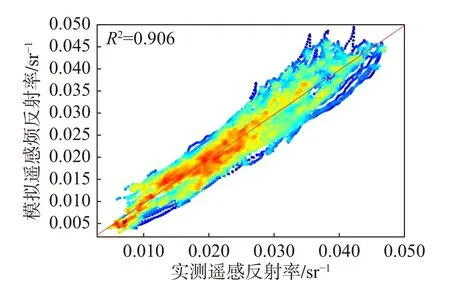
图4 模拟反射率与实测反射率拟合Fig.4 Fitting of simulated reflectance and measured reflectance

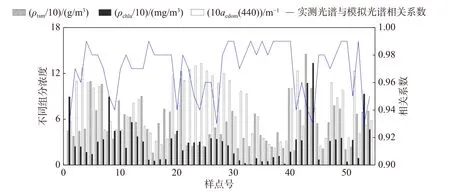
图5 每个样点的实测浓度数据以及其模拟光谱和实测光谱的相关系数Fig.5 The measured concentration data of each sample point and the correlation coefficient between the simulated and measured spectrum

3.2 相关性分析结果

为分析在不同区间的悬浮物浓度范围下，不同反射率组合与悬浮物、叶绿素a 及CDOM 的相关关系。根据聚类方法中的贝叶斯准则确定区间个数为3，然后对分界点取整数，据此把样点划分为15~48 g/m3、48~80 g/m3以及80~145 g/m3三个范围等级。在这3 个悬浮物浓度范围以及整个悬浮物浓度范围（15~145 g/m3）下，进行悬浮物浓度、叶绿素a 浓度、CDOM 浓度（以下简称三要素浓度）与20 个比值反射率组合和20 个差值反射率组合的相关性分析（结果如图6 和图7 所示），主要结论如下：

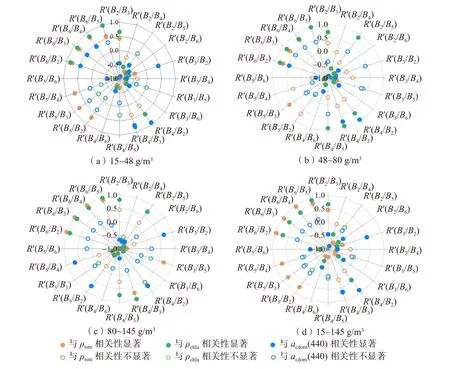
图6 不同浓度范围下比值组合反射率与三要素浓度的相关性Fig.6 Correlation between ratio combined reflectance and three-element concentration in different concentration ranges

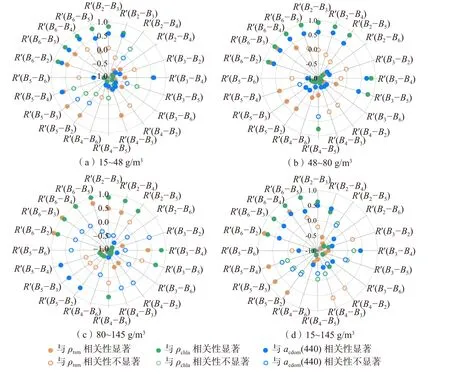
图7 不同浓度范围下差值组合反射率与三要素浓度的相关性Fig.7 Correlation between differential combined reflectance and three-element concentration at different concentration ranges

1） 在区分浓度区间时，与悬浮物浓度显著相关性高于0.7 的比值组合分别占比45%、15%和55%，而显著相关性高于0.7 的差值组合分别占比10%、20%和40%；在不区分浓度区间的情况下，与悬浮物浓度显著相关程度高于0.7 的比值组合和差值组合均占比50%。

2） 在区分浓度区间时，叶绿素a 浓度与不同反射率组合的显著相关性，在悬浮物浓度为15~48 g/m3时明显低于另外两个浓度区间；不区分浓度区间时，与叶绿素a 浓度显著相关程度高于0.7 的比值组合和差值组合分别占比15%和40%。

3） 在区分浓度区间时，CDOM 浓度与比值组合的显著相关性，在三个浓度区间下均高于差值组合；不区分浓度区间时，CDOM 浓度与比值组合的显著相关程度高于0.7 的占比10%，而与差值组合的相关性均在0.5 以下。

4） 进一步综合分析三要素相关性，存在着与悬浮物浓度表现为显著相关性，又与叶绿素a 浓度（或CDOM 浓度）呈显著相关的反射率组合，这些组合并不适合用于悬浮物浓度反演。在区分浓度区间时，不只与悬浮物浓度显著相关的比值组合分别占比55%、35%和50%，差值组合分别占比40%、55%和70%；不区分浓度区间时，不只与悬浮物浓度显著相关的比值组合和差值组合分别占比50%和40%。

因此，为避免叶绿素a、CDOM 对悬浮物反演的影响，需要从中筛选出只与悬浮物浓度呈显著相关的组合，看作是悬浮物浓度敏感特征因子，再比较它们与三要素浓度的相关特征，寻求只与悬浮物浓度存在较强显著相关性的敏感因子。不同浓度区间和整个浓度区间三要素浓度与悬浮物浓度敏感因子的相关性特征结果如表1 所示。综合分析发现，R′(B5/B3)只与悬浮物浓度表现为较强的显著相关性，与叶绿素a 和CDOM 浓度相关性均不明显，因此直接选取R′(B5/B3)作为反演因子来构建悬浮物浓度反演模型。

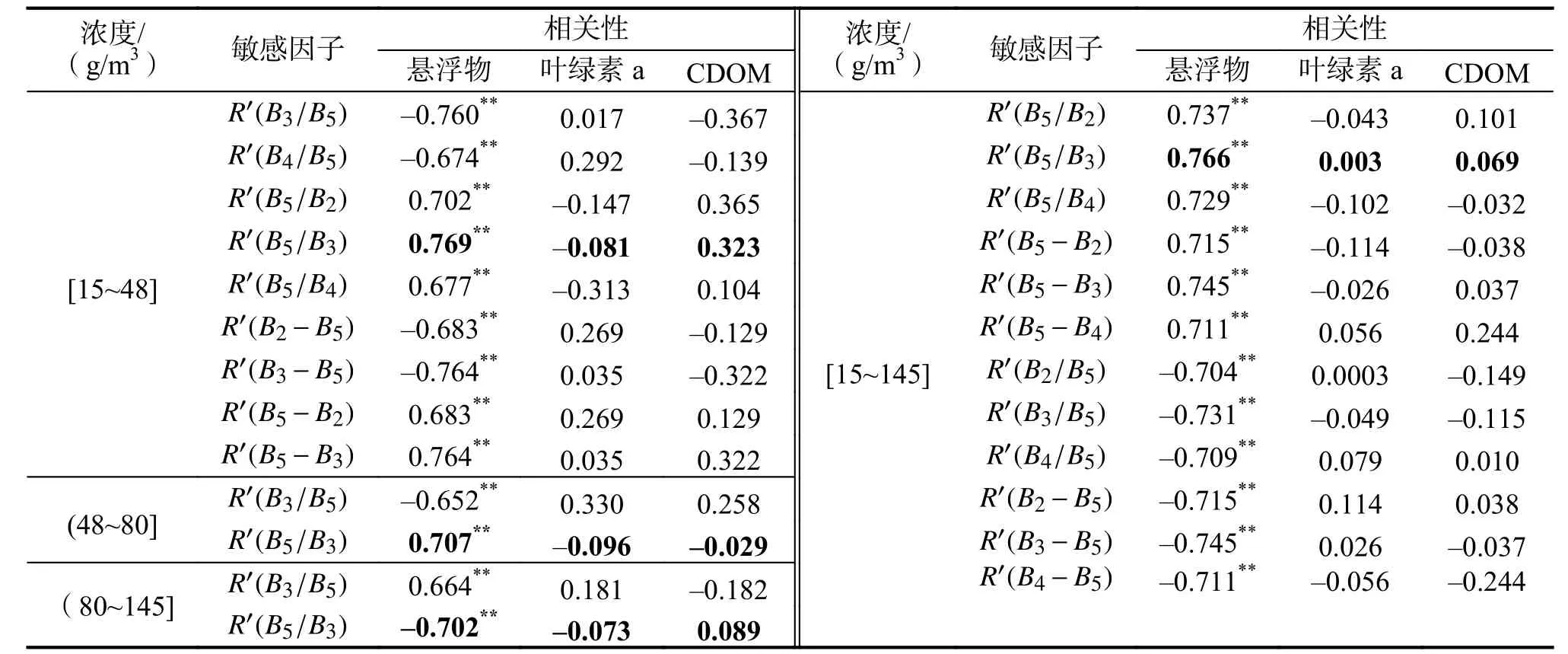
表1 不同浓度区间悬浮物敏感因子的相关性特征Tab.1 Correlation characteristics of suspended matter sensitivity factors

3.3 反演模型构建结果

在相关性分析基础上，以反演因子R′(B5/B3)为自变量x、悬浮物浓度为因变量来构建不同反演模型，具体构建结果如表2 所示。可以发现，构建的模型决定系数均在0.75 以上，其中幂函数模型（图8）的R2值较高（R2=0.817），拟合关系较为理想，建模误差较小（ERMS=9.89 g/m3，EMAP=1 3.39%，ENRMS=18.97%）。

表2 以 R ′(B5/B3)为反演因子构建的不同反演模型Tab.2 Comparison of different suspended matter concentration retrieval models constructed with R ′(B5/B3) as the retrieval factor

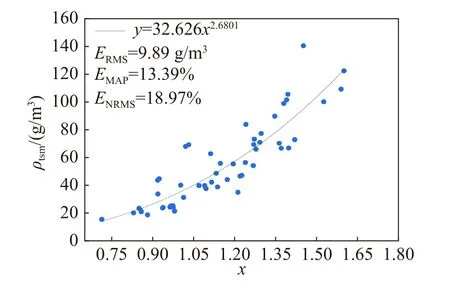
图8 以 R ′(B5/B3)为反演因子的最佳拟合模型Fig.8 Best fit model with R ′(B5/B3) as the retrieval factor

3.4 反演模型验证结果

3.4.1 基于实测数据验证

将构建的最佳拟合模型应用到太湖实测数据集1 中，对于实测数据，模型应用效果较好，整个悬 浮 物 浓 度 区 间的ERMS为13.70 g/m3，EMAP为18.47%，ENRMS为20.83%。实测值与反演值的拟合结果显示两者具有线性关系（图9），说明以R′(B5/B3)为反演因子构建的模型反演结果与现场测量结果有一致性。然而随着浓度的增加，模型应用效果变差，当悬浮物浓度大于80 g/m3时，偏离1∶1 参考线程度较大，为分析原因进一步统计了不同浓度区间对应的样点个数和误差情况，统计结果如表3 所示。由表3 可以发现，80~145 g/m3浓度区间的ERMS、EMAP和ENRMS明显高于15~48 g/m3和48~80 g/m3，造成该现象的原因可能与反演模型构建过程中大于80 g/m3的高浓度样点数量偏少（比例仅为14.8%）有关。

表3 不同浓度区间的误差统计Tab.3 Error statistics in different concentration intervals

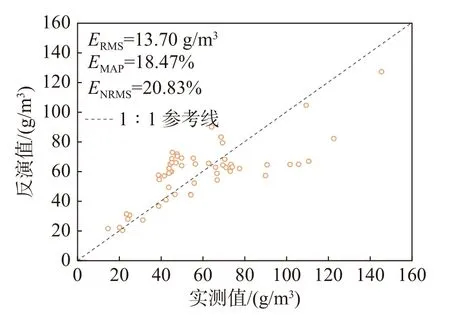
图9 基于数据集1 的悬浮物浓度反演值与实测值拟合Fig.9 Fitting the suspended matter concentration retrieval value with the measured value based on the

3.4.2 SDGSAT-1 影像悬浮物浓度反演与验证

将反演模型应用到2022 年5 月4 日SDGSAT-1 影像，并利用地面与卫星同步实测数据对反演结果进行验证，结果如图10 所示。可以看出悬浮物反演值和实测值基本分布在1∶1 参考线附近，ERMS为4.78 g/m3，EMAP为15.42%，ENRMS为20.19%，说明反演模型对于太湖地区的SDGSAT-1 影像悬浮物浓度具有较高的反演精度，适用性较强。

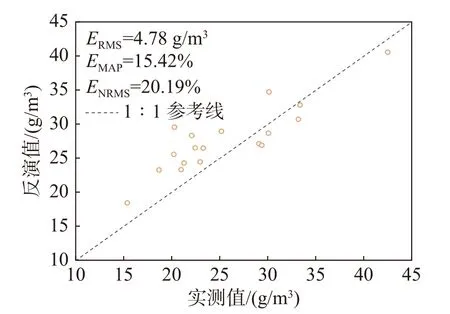
图10 基于数据集2 的悬浮物浓度反演值与实测值拟合Fig.10 Fitting the inversion values of suspended matter concentration with the measured values based on the dataset 2

太湖水域悬浮物浓度反演结果的整体空间分布如图11 所示。该影像的卫星过境时间正处于5 月初，太湖悬浮物反演结果为0~60 g/m3，整体处于中低浓度水平，空间上具有差异性，分布特点为湖心和东部水域悬浮物浓度较低，而西部作为开放水域悬浮物浓度较高，太湖作为浅水湖泊，其开放水域在风力驱动下出现泥沙再悬浮特征，且有向湖内聚集的趋势。

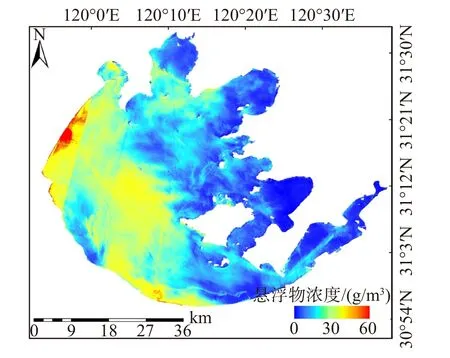
图11 2022 年5 月4 日太湖SDGSAT-1 影像悬浮物浓度反演值空间分布Fig.11 Spatial distribution of suspended matter concentration inversion in SDGSAT-1 image of Lake Taihu on May 4,

4 结束语

水体中的悬浮物会引起水污染的发生，监测水体中的悬浮物对了解、掌握和改善水环境问题至关重要。由于水体反射率是水体中不同组分（叶绿素a、悬浮物、CDOM）累计相互作用的结果，为限制叶绿素a、CDOM 的作用，本文针对SDGSAT-1 卫星MII 传感器特点，以太湖为例，利用Hydrolight 模型从机理上探明了只与悬浮物浓度强相关而与叶绿素a、CDOM 弱相关的特征敏感因子，并据此建立了适用于SDGSAT-1 MII 影像的太湖悬浮物浓度反演模型，进一步探讨了模型对SDGSAT-1 数据的适用性。得出如下结论：

1） 基于Hydrolight 模型模拟太湖水体辐射传输过程，通过相关性分析发现R′(B5/B3)与悬浮物浓度表现显著强相关（r=0.766（p<0.01））而与叶绿素a 浓度、CDOM 浓度相关性较弱（r=0.003、0.069），说明该组合是构建悬浮物浓度反演模型的最佳波段组合。

2） 以R′(B5/B3)为反演因子，构建的不同形式的悬浮物浓度反演模型的决定系数均在0.75 以上，其中幂函数模型为最优反演模型

3） 将构建的模型分别应用于实测数据和SDGSAT-1影像数据，ERMS分别为13.70 g/m3和4.78 g/m3，EMAP分别为18.47%和15.42%，ENRMS分别为20.83%和20.19%，两次验证结果表明反演结果和现场测量结果具有较强一致性。

本研究构建的SDGSAT-1 悬浮物浓度反演模型在太湖地区具有良好的适用性，同时也表明SDGSAT-1卫星在悬浮物浓度遥感反演中有着较强的应用潜力，能够为太湖以及其他内陆水体的水环境监测与改善提供重要抓手。

致谢感谢可持续发展大数据国际研究中心（International Research Center of Big Data for Sustainable Development Goals）提供的SDGSAT-1 卫星数据！