让数学思想植根于数学课堂
周慧
“植树问题”的教学旨在引导学生发现数学规律,建立“植树问题”模型,并在实际生活中加以应用,发展数学应用意识。教学中,教师如何把握“植树问题”的核心目标?如何设计结构化的教学环节、教学活动?如何渗透数形结合等思想方法,提高学生解决问题的能力?本期,我们从“数学思想”角度精选三篇文章,讨论“植树问题”的教学策略。
数学思想对数学发展起到关键作用。小學数学课堂教学中,教师如何使学生领悟数学思想的内涵,并自觉利用数学思想探究问题、解决问题,彰显数学学科的育人价值呢?笔者以“植树问题”的教学为例,做具体阐释。
一、如何理解“植树问题”
“植树问题”需要教什么?大家一般会认为,三种类型“植树问题”的棵数与间隔数的关系是教学重点,即两端要栽、一端栽一端不栽、两端不栽的模型建立是教学重点。事实上,这样缺乏结构化理解的教学是零散的,不一定能取得好的效果。笔者认为,这三种类型不是并列的关系,而是层级关系,因此教学时不能平均用力。“一端栽一端不栽”这种类型可以看作“主干”,因为它的棵数与间隔数能一一对应,即“棵数=间隔数”,其算理与二年级学习的除法相通,都体现了一一对应,商可以直接作为问题的答案。教师在教学中将“一端栽一端不栽”植树问题的教学与除法关联起来,学生的学习就有了扎实的基础。其他两种类型(两端要栽、两端不栽)可以在这个类型的基础上进一步建构。“两端要栽、两端不栽”情况下棵数与段数不是一一对应的,因此需要在一一对应的基础上“+1”或“-1”,这两种类型可以看作“分枝”。
教师在教学时应该把重点放在理解“一一对应”及“商+1”或“商-1”的道理上,如此,教学就有了结构,“植树问题”就变成了基于旧知识的拓展运用。由此,笔者认为学生掌握“植树问题”的基础和关键是与除法的意义建立关联,而不是机械地记忆棵数与间隔数的数量关系。
二、掌握“植树问题”的关键是什么
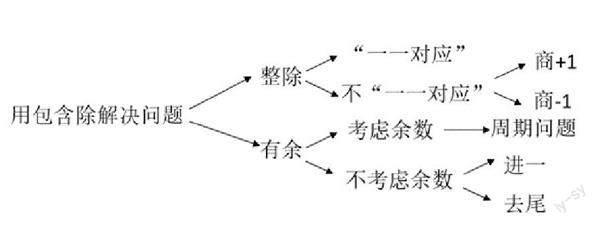
“植树问题”模型并不是三种不同的类型,而是只有一个“源”,即用“包含除”解决问题。“包含除”涉及两类问题,一类是当商是整数时,要么能“一一对应”,要么需要根据实际情况对商进行“+1”或“-1”,后两种是变式;另一类是当商不是整数而有余数时,需要根据实际问题对余数进行“进一”和“去尾”的处理。思维导图如下图所示。
由此可知,教学“植树问题”的首要任务是让学生建立“一端栽一端不栽”植树问题与除法意义的关联,打通新旧知识之间的联系,并在原有的除法体系里进行拓展,以解决变式问题(两端要栽、两端不栽)。这样教学有助于学生理解和应用“植树问题”模型,减轻他们的学习负担。
三、“植树问题”要根植哪些数学思想
1.感悟化繁为简思想
课堂上,笔者用课件出示问题:“村里新修了一条平安大道。绿化工人要在长200米的平安大道的一边植树(每隔5米栽一棵,两端要栽),一共需要栽多少棵树苗?”出示问题后,笔者提问“每隔5米栽一棵,两端要栽是什么意思”,并让学生猜一猜“一共需要多少棵树”。有的学生说“能种40棵”,有的学生说“能种41棵”,还有的学生说“能种39棵”。笔者启发学生思考:“到底能种几棵?你有什么好的验证方法吗?”一名学生提出:“我们可以试着种一种。”笔者肯定了学生的想法并引导:“我们可以利用课件模拟在200米的线段上种树。”随后,笔者用课件演示“每隔5米种一棵,一棵一棵不停地种”的动态过程。这时,一名学生质疑:“这样要花很长时间,很麻烦。”另一名学生建议:“我们可以换成短一点的距离,比如将200米换成20米,用比较小的数据研究出植树规律。”笔者肯定了学生的想法,指出先探究在较短距离的路上共种几棵树的一般规律,再用这种规律去解决较复杂的问题,是一个不错的办法。这样教学,化繁为简的数学思想得以有效凸显。
2.感悟数形结合思想
在解决问题中采用数形结合思想能帮助学生更好地理清数量之间的关系,明确解题思路,确定有效的解题方法。
教学“植树问题”时,笔者引导学生借助直观图形进行分析,并从图形中归纳、总结出一般的解题方法。课堂上,笔者先让学生画图,模拟植树,验证在20米的道路的一边植树,每隔5米栽一棵,两端要栽,可以栽几棵。有的学生用“___”代表间隔,用“\”代表一棵树,画出图示“\___\___\___\ ___\ ”;有的学生用“___”代表间隔,用“●”代表一棵树,画出图示“●___●___●___● ___●”。笔者引导学生观察图示,学生发现棵数比间隔数多1。这样教学,学生借助图形直观感知到两端要栽时棵数与间隔数之间的数量关系(棵数=间隔数+1),感悟到数形结合思想的应用价值。
3.感悟一一对应思想
教学“植树问题”时,教师可以渗透一一对应的思想方法,帮助学生学会用一一对应的数学思想解决问题。
“植树问题”的本质是对应,学生只要明确“植树间隔”与“树的棵数”之间的对应关系,并以此为基础深入探究,就可以应对各种变式情况。在学生发现两端要栽情况下“棵数=间隔数+1”的数量关系后,笔者追问“为什么棵数比间隔数多1”,引导学生用一一对应的方法分析问题。学生指着图示分析道:“一棵树后面跟着一个间隔,也就是一棵树对应一个间隔,最后一棵树没有间隔与之对应,所以棵数比间隔数多1。”种树还可能出现什么情况?学生发现,还可能出现“一端栽一端不栽”和“两端不栽”的情况,并且都能用一一对应的思想方法解释这两种情况下棵数与间隔数的关系,从而感悟到一一对应数学思想的应用价值。
4.感悟数学模型思想
“植树问题”的教学过程就是数学模型建立的过程,教师应该让学生经历“猜想—验证—建模—应用”的学习过程,以更好地理解和掌握“植树问题”模型。教学时,笔者把重点放在让学生积极探索并发现“植树问题”的解题规律上,着力激发学生的好奇心和求知欲,把“植树问题”作为学生感悟数学思想方法的支点,引导学生感悟数学建模的重要意义。
当学生掌握了“两端要栽”的模型后,笔者引导学生探究“一端栽一端不栽”和“两端不栽”的情况。笔者先请学生独立思考每种情况的棵数与间隔数,再把这些数据整理成表格,然后对比分析(表略)。通过探究,学生构建了“两端要栽:棵数=间隔数+1”“一端栽一端不栽:棵数=间隔数”“两端不栽:棵数=间隔数-1”三种模型。建立“植树问题”模型后,学生要用模型解决生活中的实际问题,以此提高解决问题的能力。教师可以通过不同的变式练习,比如求总长、求间隔、求间隔数、求棵数等问题,以及锯木头、爬楼梯、开业剪彩等问题,让学生拓展应用“植树问题”数学模型,使其感悟到模型思想对于解决数学问题的价值。
(作者单位:襄阳市保康县马桥镇小学)
责任编辑 张敏

