基于WBOA的3D-DV-Hop节点定位算法*

彭 铎，张腾飞，黎锁平，杨雅文

（1.兰州理工大学计算机与通信学院，甘肃 兰州 730050；2.兰州理工大学理学院，甘肃 兰州 730050）

0 引 言

无线传感器网络（wireless sensor networks，WSNs）［1］的节点用来感知、采集、处理网络分布比较危险复杂区域内的检测对象的位置及其信息，所以，节点定位成为WSNs的关键问题之一，也是该领域的研究热点［2］。而这些危险复杂区域的地貌通常都是三维（3D）的，因此，3D节点定位至今仍是研究热点［3］。

3D-DV-Hop（distance vector hop）是典型的非测距定位算法，存在定位精度不高的缺陷。文献［4］提出了一种自适应免疫粒子群与DV-Hop 融合算法，优化了位置估计阶段，有效的提高了算法的定位精度。文献［5］提出的算法通过对跳数、跳距优化，用改进粒子群算法优化位置坐标来提高算法定位精度。文献［6］提出了基于弹簧系数和接收信号强度指示的DV-Hop 的改进算法，通过引入弹簧模型改进最小跳数与平均跳距，提高了算法的定位精度。文献［7］针对3D-DV-Hop全局跳数划分不够精确，利用锚节点的平均跳距估算距离时导致定位误差大的问题，提出一种基于多通信半径和跳距加权的WSNs 3D迭代定位算法。文献［8］通过创建权值与跳数的数学模型，利用遗传算法对该定位模型进行全局最优求解，使得模型定位误差收敛到1／4。文献［9］提出了一种改进的基于邻近节点信息的3D-DV-Hop算法，该算法通过计算未知节点的跳数，消除了节点间的一次通信，降低了网络的功耗。文献［10］提出了一种基于改进的狮子群优化算法的3D-DV-Hop定位方法，该算法利用群智能优化算法用于未知节点坐标的优化，没有考虑平均跳距误差过大造成节点定位精度低的情况。

为了更加拟合现实环境状况，网络节点分布变得比较随机，可能会出现某一节点在其他节点的通信范围之外，导致此节点无法与其他节点通信或者无法定位，（后文将这些节点统称为孤立点，在3.1 节说明），将这些节点去除。对于由平均跳距估算距离时出现误差较大的问题，本文首先利用修正因子修正平均跳距，然后利用修正的平均跳距估算的距离与实际距离的差值函数作为目标函数，用自适应权重改进后的蝴蝶优化算法（butterfly optimization algorithm，BOA）求得全局最优平均跳距。

1 3D-DV-Hop定位算法

1.1 3D-DV-Hop算法步骤

3D-DV-Hop 定位算法是二维DV-Hop 定位算法［11］的扩展，是一种距离无关的定位算法，其算法主要有3 个阶段：

步骤1 计算锚节点与每个未知节点的最小跳数

所有锚节点以多跳的方式向网络中广播自身数据包，信息发出的锚节点的跳数为0，数据包每经过一个节点，跳数加1，当一个节点收到多个跳数信息时，保存跳数值最小的一条信息。

步骤2 计算锚节点的平均每跳距离

利用式（1）估算平均每跳距离

式中 （xi，yi，zi）和（xj，yj，zj）为锚节点i和j的坐标，hopi，j为锚节点i到锚节点j的跳数，hopsizei为锚节点i的平均跳距。

步骤3 利用极大似然估计法计算自身坐标

未知节点通过式（2）计算它和锚节点之间的距离Di，j，然后根据最小二乘法就能得到未知节点的坐标

式中Di，j为锚节点i和未知节点j之间的距离，hopi，j为锚节点i和未知节点j之间的最小跳数。

1.2 DV-Hop算法的误差分析

由于网络拓扑的随机性，当网络区域大，节点数少或通信半径短时，网络中会出现一些孤立点，导致实验不能有效进行，且离锚节点距离越远的未知节点累积的误差越大。

利用极大似然估计法计算未知节点坐标时，需要知道锚节点与未知节点的估计距离，由于两节点之间的跳距往往并不相等，利用锚节点的平均跳距估算距离时也会产生较大的误差。

2 BOA

根据蝴蝶的觅食行为，提出了一种新的全局优化元启发式算法--BOA［12］。BOA模仿蝴蝶觅食这种行为来寻找超搜索空间中的最优解。

蝴蝶的自然现象受变量I和对香味感知度f的影响，算法的变量I与目标函数相关联。在BOA中，香味是物理刺激强度的函数，公式如下

式中f为对香味的感知程度，即其他蝴蝶对香味的感知程度，c为感觉模态，I为刺激强度，a为与模态有关的幂指数，反映了不同的吸收程度，a和c的取值范围为［0，1］。

该算法有2个关键的阶段：全局搜索阶段与局部搜索阶段。在全局搜索阶段，蝴蝶朝着香味最浓的方向移动，即向最优的蝴蝶g*靠近。可以用式（4）来表示

式中为迭代次数为t的蝴蝶的解向量。g*为当前迭代中所有解中找到的当前最佳解，r为（0，1）中的随机数。

局部搜索阶段可以表示为

式中和为解空间中的第j个和第k个蝴蝶的解向量。如果和属于同一个种群，并且r为（0，1）中的随机数，则式（5）为局部随机游走。在BOA 中使用切换概率在全局搜索和局部搜索之间切换，由文献［13］测试可知，p＝0.8对算法最有益。

3 3D-DV-Hop定位算法

3.1 去除孤立点

在该算法中，如果某一节点到与其他超过总节点数50%节点的跳数的返回值为无穷大，那么称这个节点为孤立点。去除孤立点的过程如下：

1）节点i与a个节点不能通信，判断a是否大于总节点数的50%；

2）若是，则将节点i确定为孤立点，并分别记录锚节点与未知节点中存在的孤立点个数；

3）从锚节点和未知节点中去除这些孤立点，然后重新初始化节点个数及节点间的距离与跳数。

3.2 修正平均每跳距离

由DV-Hop算法的误差分析得知，锚节点的平均跳距是影响定位精度的主要原因。因此本文添加了修正因子优化锚节点的平均跳距。

改进步骤如下：

步骤1 根据式（1）求得每个锚节点的每跳平均距离hopsizei，则2个锚节点i，j之间的估计距离Dij为

步骤2 锚节点i，j之间的实际距离可以由其坐标计算得到

步骤3 根据式（6）和式（7），锚节点i，j之间的距离误差dij可表示为

步骤4 根据距离误差dij计算锚节点i的修正因子

ci为

此时，锚节点i的平均每跳距离hopsizei可表示为

步骤5 利用修正后的平均跳距计算锚节点i，j之间的估计距离D公式为

3.3 求取最优平均跳距

求取最优平均跳距分为3个步骤：

步骤1 初始化阶段，算法定义目标函数及其解空间，为BOA中使用的参数赋值，创建一个用于优化的蝴蝶初始种群。

设锚节点i对应的平均跳距为hopsizei，ε为平均跳距引起的误差，合理的hopsizei应使ε最小，由式（7）和式（11）可得

由此，可知适应度函数如下

使用式（3）计算蝴蝶的香味。在求解最优平均跳距hopsizei时，在搜索空间中随机生成蝴蝶的位置，计算并存储它们的香味值和适应度值。

步骤2 迭代阶段，由算法进行多次迭代。

基本的BOA 存在收敛精度较低，全局搜索能力不足，容易陷入局部最优的缺陷。受文献［13］的启发，为了平衡全局搜索与局部搜索的能力，算法采用自适应权重处理的方法。

当权重比较大时，算法的全局搜索能力较强，可以搜索较大的区域；当权重比较小时，算法的局部搜索能力较强。采用如式（14）所示的权重因子对全局搜索阶段进行加权，使得算法易跳出局部最优，提高了算法的全局搜索能力

改进后的全局搜索阶段如式（15）所示

采用式（16）的所示的权重因子对局部搜索阶段进行加权，提高了算法的局部搜索能力，加快了算法的收敛精度

改进后的局部搜索阶段如式（17）所示

由开关概率p判断算法是进行全局搜索还是局部搜索，若r＜p，则算法进行全局搜索，由式（15）来寻优，若r≥p，则算法进行局部搜索，由式（17）来寻优。然后判断寻找的最优值是否在所设特定条件之内发生，若是，更新最优解，算法更新感觉模态c，进行下次迭代，直到达到最大迭代次数，算法停止。

步骤3 当迭代阶段结束时，算法输出找到具有最佳适应度的hopsizei的最佳解。

在该算法中，将利用自适应权重因子改进的BOA命名为WBOA（weighted BOA）。

3.4 利用极大似然估计法计算自身坐标

未知节点接收到改进后的最优平均每跳距离，通过式（2）计算它和锚节点之间的距离Di，j，然后根据极大似然估计法能得到未知节点的坐标。该算法的流程如图1 所示。

图1 算法流程

4 算法仿真与结果分析

4.1 WBOA的优化性能分析

为了进一步验证WBOA在求解此定位问题的有效性，将WBOA 与BOA、鲸鱼优化算法（whale optimization algorithm，WOA）［14］以及花授粉算法（flower pollination algorithm，FPA）［15］进行对比。为了实验的公平、客观性，选取与式（13）维数一致的基本测试函数式（18）来验证WBOA的寻优性能，范围为［-100，100］，WBOA 和BOA 中的c感官形态设置为0.01，幂指数a为0. 1，切换概率p为0.8，所有算法的初始种群规模统一设为30，迭代次数设置为500，4个算法的共有参数保持一致

算法的寻优质量由最优值和最差值反映，从表1 数据中可知，对求解函数f时，WBOA 能寻到理论最优值0，说明，在求解此类函数，WBOA 的寻优性能最强，明显优于BOA、WOA、FPA。

表1 测试函数实验结果比较

为了直观展现WBOA的寻优性能，本文给出测试函数的收敛曲线，如图2 所示。由函数的收敛曲线可以直观地看出改进后的算法WBOA的收敛精度更高，解决了基本算法BOA寻优精度不高的问题。

图2 收敛曲线

4.2 基于WBOA的3D-DV-Hop算法参数设置

为了验证本文算法的定位性能，利用MATLAB 2018a对基于WBOA的3D-DV-Hop、3D-DV-Hop算法和文献［10］中提出的算法，从锚节点个数、通信半径大小和总节点个数等3个方面进行仿真实验分析。在100 m ×100 m ×100 m的仿真区域内，随机产生一定数量的网络节点。算法的参数设置如表2所示。

表2 基于WBOA的3D-DV-Hop算法相关参数设置

网络的平均定位误差计算公式如下

式中 （xi，yi，zi）与（x′i，y′i，z′i）为未知节点i的实际坐标和估计坐标，R为锚节点的通信半径，N为未知节点的总数。

4.3 仿真实验分析

图3是节点总数为100，网络通信半径为30 m时，锚节点个数的变化对网络节点平均定位误差的影响，从图中可以看出，3种算法在随着锚节点个数增加时平均定位误差都有不同程度的降低。其原因是锚节点的个数增加，则其密度增大，未知节点从距离最近的锚节点获取的平均跳距时更加接近其自身的平均跳距，从而使得平均定位误差降低。在相同的条件下，基于WBOA的3D-DV-Hop算法的平均定位误差最小，当锚节点的比例在20%～30%之间时，基于WBOA的3D-DV-Hop 算法的平均定位误差相比于文献［10］算法降低了10%～15%；当锚节点的比例在35%～50%之间时，基于WBOA 的3D-DV-Hop 算法的平均定位误差相比于文献［10］算法降低了3%～6%。

图3 锚节点数对平均定位误差的影响

图4 是节点总数为100，网络通信半径为40 m时，锚节点个数的变化对网络节点平均定位误差的影响，与图3 相比，通信半径增大，3种定位算法的平均定位误差都有了不同程度的下降，是因为随着跳数的增加，未知节点的累积误差也会增大，而通信半径增大时，节点间的跳数随之减少，则未知节点的定位误差也随之降低。由图4 可知，在相同的条件下，基于WBOA的3D-DV-Hop算法的平均定位误差一直都最小，对比于文献［10］来说，平均定位误差降低了1%左右。3种算法的平均定位误差随着锚节点的增多稳定下降，这是因为网络区域小，锚节点数增多，通信半径大，误差波动相对稳定。

图4 不同通信半径下锚节点数对平均定位误差的影响

图5 是锚节点数比例为30%，网络通信半径为30 m时，总节点个数的变化对网络节点平均定位误差的影响。从图中可以看出，随着节点总数的不断增加，3 种定位算法的平均定位误差都较为稳定的降低，这是因为节点总数增加，节点的密度提高，网络的连通性变好，孤立点减少，网络可以收集更多的定位信息用于未知节点的定位。在相同的条件下，本文算法的平均定位误差一直都最小，与文献［10］算法比较而言，本文算法的平均定位误差大致降低了5%左右。而当节点总数在100 ～120 之间时，本文算法明显更加优于其他两种算法，当节点数大于120 时，3 种算法的平均定位误差随着节点总数的增加逐渐降低，从整体分析来看，本文算法的优势更加突出。

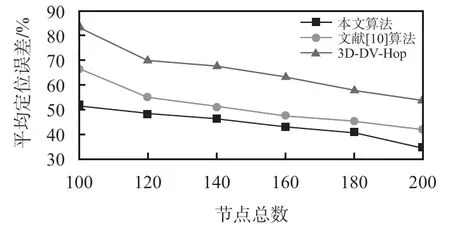
图5 节点总数对平均定位误差的影响

4.4 算法的时间复杂度分析

时间复杂度反应了算法执行的时间长短。算法中所涉及的网络节点规模大小与节点总数n相关，锚节点的数为m。则3D-DV-Hop算法的时间复杂度为O（n3）；文献［10］算法在3D-DV-Hop 算法的基础上增加的时间复杂度为O（n（n-m）2）；本文算法在3D-DV-Hop算法的基础上增加的时间复杂度为O（n×m），由此可知：本文算法相比较文献［10］算法时间复杂度略小一些。

4.5 计算开销分析

将算法的平均运行时间作为算法开销指标进行分析。表3为相同实验条件下所统计的3 种算法的平均运行时间。由实验结果可知：本文算法的平均运行时间比文献［10］算法小，但大于3D-DV-Hop 算法，因为本文算法添加了修正因子和智能优化算法导致运算量加大，计算开销略有增加，但是定位精度明显提升。

表3 3 种算法的平均运行时间

5 结束语

本文考虑了3D-DV-Hop定位算法孤立点的存在，以及利用锚节点的平均跳距估算到未知节点之间的距离时误差较大的问题。提出了一种基于WBOA 的3D-DV-Hop 节点定位算法。该算法首先去除了网络中可能存在的孤立点，然后重新计算节点个数以及节点间的距离与跳数，之后对锚节点的平均跳距进行了修正，接下来利用自适应权重平衡全局搜索与局部搜索能力，使算法不易陷入局部最优，加快了算法的收敛精度，得到全局最优平均跳距。从定位精度来看，本文改进的算法明显优于传统定位算法，具有较好的实用价值。未来3D-DV-Hop定位可能的研究热点是移动网络、不规则拓扑网络和基于多目标优化模型的定位算法。