变压器长圆形绕组振动仿真与机械故障诊断研究*

陈朝阳，杨文荣，张雨蒙，石小晖

（河北工业大学省部共建电工装备可靠性与智能化国家重点实验室，天津 300130）

0 引 言

为保障国民经济提供可靠的能源供应，亟需制定动态检修策略，进而量化故障带来的风险。变压器机械故障属于潜在性故障，初期大多是由机械结构问题所引起，其中绕组故障所占比重较大［1］。配电变压器绕组从外观结构上有圆形、长圆形、椭圆形等形状，长圆形绕组设计具有优良的节材效果，广泛应用于中小型配电变压器设计中［2］。长圆形绕组的配电变压器向大容量方向发展，在配电网中大力推广，长圆形绕组因机械性能较差，外部短路事故时有发生，影响其使用寿命［3］，因此，对长圆形绕组进行早期机械故障诊断具有重要意义。

目前，针对长圆形绕组的机械故障诊断研究较少，主要研究圆形绕组松动、形变等故障最多［4，5］。针对圆形绕组机械故障诊断，Wu Y Y等人［6］采用麻雀搜索算法（sparrow search algorithm，SSA）与深度信念网络（deep belief network，DBN）相结合的方法对振动信号的特征向量进行分类，可以有效提高分类算法的分类精度5 %～20 %。Zhou L J 等人［7］提出基于二叉树支持向量机（binary tree support vector machine，BT-SVM）的诊断模型，可以解决小样本学习的问题，可用于电力变压器的机械故障诊断。但上述方法存在特征提取量较大、诊断过程较为复杂的问题，不利于实时在线故障诊断。因此，设计一种算法流程简单、样本点少、诊断速度快的故障诊断方法是有必要的。

针对长圆形绕组更容易产生位移形变的问题，本文首先建立了长圆形绕组辐向和轴向数学模型，分析其不同方向上的振动特性；其次，建立长圆形绕组的有限元仿真模型，分析其不同位置的振动特性；最后，设计绕组松动和翘曲故障实验，针对绕组薄弱位置进行小波包能量特征提取，采用灰狼优化（grey wolf optimization，GWO）算法优化SVM参数的方法对长圆形绕组不同机械状态进行故障诊断。

1 变压器长圆形绕组振动数学模型分析

长圆形高压和低压绕组辐向电磁力如图1所示。

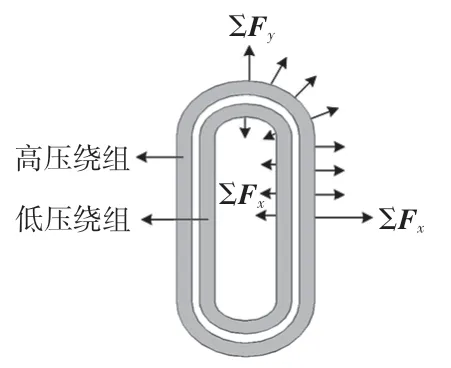
图1 辐向电磁力示意

由图1可发现，长圆形绕组的辐向电磁力Fx比辐向电磁力Fy强，Fx易使高、低压绕组导线被拉长，进而发生永久形变；此外，匝间绝缘也被拉长，导致匝间绝缘破裂，进而形成匝间短路。

对于工频电流为i＝Imcosωt的长圆形绕组，将其振动过程分解为辐向和轴向

式中Fr和Fz分别为辐向和轴向电磁力，kz和kr分别为绕组轴向和辐向坐标的相关系数矩阵，Im为绕组电流的有效值。

1.1 绕组辐向振动数学模型

建立绕组辐向振动的动力学方程为

式中M为质量矩阵，Cr为辐向阻尼矩阵，μ为摩擦系数，zr为各节点辐向位移列向量。

式（2）的齐次通解为

式中D1，D2为常数，与绕组振动初始条件有关。

式（2）有两项特解，第一项特解为

第二项特解为

绕组辐向振动的动力学方程通解为

在负载电流不变的条件下，绕组辐向振动位移与绕组质量、辐向阻尼、绝缘树脂与垫块的摩擦系数、绕组预紧力及绕组位置有关，主要振动频率为基频（100 Hz）及其倍频。

1.2 绕组轴向振动数学模型

建立绕组轴向振动的动力学方程为

式中 zz为各节点轴向位移列向量。Cz为轴向阻尼矩阵，轴向刚度矩阵K。

式（7）的齐次通解为

式中A1和θ取决于方程初始条件的积分常数。

式（7）有两项特解，第一项特解为

第二项特解为

绕组轴向振动的动力学方程通解为

在负载电流不变的条件下，绕组轴向振动位移与绕组质量、刚度、轴向阻尼、预紧力及绕组位置有关，主要振动频率为基频100 Hz。

当绕组发生结构变形时，主要改变100 Hz倍频的振动；当绕组发生松动时，主要影响基频100 Hz的振动，即机械状态改变引起振动特征的改变。因此，通过监测变压器的振动信号可以评估绕组的机械状态。

2 长圆形绕组机械故障有限元仿真

在中性点接地方式中，单相绕组故障为变压器故障的主要类型，占变压器绕组故障数量的50%以上。因此，以一台SC10-30／10.5干式变压器为研究对象，绕组为长圆形结构，设计单相绕组松动和翘曲故障。

建立三维模型时，沿叠片铁心中心平面取求解域总体的1／2，变压器长圆形绕组有限元仿真参数设置：额定电流为1.65／43.3A，匝数比为525／20，相对介电常数为3.56，密度为4 450 kg／m3，弹性模量为11 ×103MPa，泊松比为0.35。

数值计算了时间同为0.326 s的A相绕组正常、松动和翘曲状态下的位移分布，如图2所示。

图2 绕组振动位移分布

从图2（a）中可以看出，绕组yoz平面中间位置处（R点）的振动位移最大，最大振动位移为4. 82 ×10-6mm，表明该处绕组易发生辐向形变，即该处为绕组薄弱点；由图2（b）可看出，绕组松动时振动位移分布发生改变，其最大振动位移向绕组端部的松动处移动，最大振动位移为7.87 ×10-6mm；图2（c）为绕组翘曲时的振动位移分布，翘曲后的振动位移分布不发生改变，但振动幅值减小，最大振动位移为1.36 ×10-6mm。由于绕组发生松动与辐向形变具有累积特性，即当绕组存在松动和较小形变时会导致其抗短路能力下降，经过长时间运行的累积从而更容易发生严重的机械故障，因此有必要对较小的机械故障进行状态监测。

3 基于GWO-SVM的长圆形绕组机械故障诊断

3.1 振动信号采集

定制SC10-30／10.5干式变压器的试验样机，将绕组外侧的绝缘板去掉，绕组线圈裸露在外。根据实际变压器故障类型及绕组的受力分析，制造了变压器绕组松动和翘曲故障，其结构如图3所示。

图3 绕组松动与翘曲故障

测试探头为356A16型压电式三轴加速度传感器，其精度为0.001 m／s2，通过振动噪声分析系统SQuadriga Ⅱ处理采集到的加速度振动信号。由第2 节仿真分析可知，可以从绕组R点的振动特性中提取变压器机械故障的特征量，因此将测试探头布置在绕组薄弱R点，试验测试如图4所示。

图4 变压器机械故障试验测试

试验时，用铜导线短接变压器的低压绕组，在高压侧施加激励电压，此时铁心振动忽略不计，加速度传感器检测到的振动信号可认为全部来源于绕组。负载电流Im在（1 ±20%）IN波动时，采集变压器绕组正常运行情况以及绕组松动和翘曲故障状态下的振动信号各20组。

3.2 小波包能量特征提取

按照能量划分表示的小波包分解结果称为小波包能量谱。小波包能量谱是基于小波包分解系数求解各个节点下的信号能量，将求解出的能量值按照顺序排列组成特征向量，可供变压器绕组故障识别使用。各节点能量计算公式为

式中M为第j个频带的长度，dj，i（n）为小波包分解后节点（j，i）对应的第n个小波包系数。

归一化处理，得到各节点能量占比D

经小波包分解后的第3层能量占比构建特征向量T

Symlets小波具备更好的对称性，在一定程度上减少信号重构时产生的相位失真。因此，对变压器绕组0～1 000 Hz范围内的振动信号进行Symlets三层小波包求解，基于分解系数求解8个节点下的信号能量，进而求解各节点能量占比。对变压器绕组正常、松动和翘曲3种不同机械状态下的振动信号进行特征提取，得到小波包分解能量谱，如图5所示。

图5 绕组小波包分解能量谱

由图5可知，故障前后的振动信号能量特征变化明显。绕组正常时，振动能量主要为D30，能量占比高于70%，D31～D37段能量占比在1%～10%不等，其中D33能量占比约为10%；绕组松动时，振动能量主要集中在D30～D33频率区间，D30占总能量的85%以上，D32次之，能量占比约为10%，相比于绕组正常，绕组松动故障导致D30频率分量占比更大，能量占比向低频段集中；绕组翘曲时，振动能量占比改变较大，D30能量占比下降至35%左右，相应的D34～D37频率区间能量占比达到60%以上。绕组翘曲位置的漏磁场较小且形状发生改变，所受电磁力减小，导致获得的D34～D37振动能量大幅增加。

3.3 GWO-SVM算法介绍

2014年，Mirjalili S等人［8］受自然中灰狼群体捕食猎物启发，首次提出了GWO算法，该算法具有收敛快，调参较少和程序简洁等特点。

该算法将灰狼群体按等级依次划分为α，β，γ和ω。在狼群中，其他灰狼必须听从和执行α狼指令，α狼被称为支配狼；β狼协助α狼做出正确的决策，并听从于α狼；γ狼支配剩余层级的狼，并听从α狼和β狼；ω狼等级最低，服从并跟随前3等级的狼对猎物进行追踪和围捕，同时平衡狼群内部关系。

式中Xp（t）为猎物的位置向量，即α，β，γ三个等级的最优解；X（t）为灰狼的位置向量，即所有可能解。D为灰狼与猎物的距离，X（t＋1）为位置更新公式，A，C为t时刻位置系数。

在狩猎过程中，由α，β，γ狼主导寻找猎物，并要求狼群根据最优解更新各自的位置，逐渐向猎物靠近，最终得到的最优解。

不同的机械状态对应不同的振动特性，可从绕组正常、松动和翘曲故障样本数据中各随机抽取10 组样本作为训练样本，其余的数据均作为测试样本，进行绕组故障诊断。SVM能够很好地处理小样本问题，更加适用于变压器绕组机械故障的分类问题。本文构建了GWO-SVM 的识别与诊断模型，具体流程如图6所示。

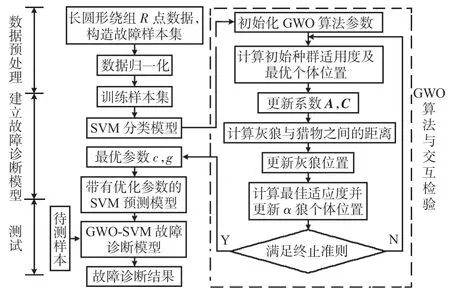
图6 GWO-SVM故障诊断流程

3.4 GWO-SVM故障诊断与结果分析

采用GWO算法优化SVM的惩罚参数c和核函数参数g，以获得模型较高的准确率。利用GWO算法优化SVM获得的最佳适应度曲线如图7所示。

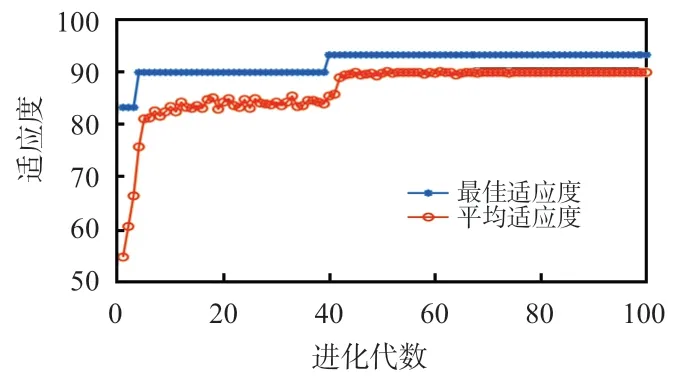
图7 GWO寻优参数适应度曲线

由图7可以看出，在适应度曲线方面，GWO在第40 次迭代时能够达到最佳与平均适应度，最优惩罚参数c为389.1，核函数参数g为0. 3，交叉验证的准确率达到93.3%。相较于人工随机选取参数而言，GWO进行参数寻优有助于节约时间、提高准确率，可以通过利用GWO 优化SVM的目标函数，从而使目标函数的准确率达到最大。未优化与GWO优化后的分类结果如图8所示，类别标签1、2、3分别表示绕组正常、绕组松动和绕组翘曲的实际状态。

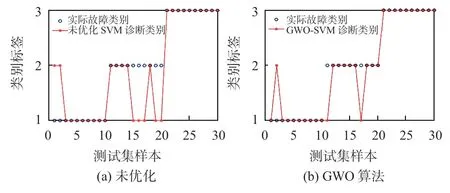
图8 优化前后SVM诊断结果分类

未优化SVM的分类结果如图8（a）所示，诊断结果中出现7个误诊结果，其中有2 个“绕组正常”和5 个“绕组松动”被误诊，未优化的SVM分类模型准确率为76.7%；采用GWO-SVM优化的分类结果如图8（b）所示，其中仅有1 个“绕组正常”和2个“绕组松动”被误诊，综合诊断的准确率达到90%。可见采用GWO-SVM的识别与诊断模型提高了绕组机械故障准确率，因此该模型可应用于实际变压器长圆形绕组机械故障诊断当中。

4 结束语

研究了长圆形绕组正常、松动和翘曲状态下的振动位移分布，在不同状态下，薄弱位置R点的能量集中程度和分布发生改变，为实验研究故障前后变压器绕组机械故障的振动特性提供分析基础。

本文采用的GWO-SVM诊断模型在变压器的机械故障诊断中具有准确率高，样本点少，泛化能力强的优势，实验结果表明，该混合优化算法综合准确率达到90%，在变压器绕组机械故障诊断中具有一定的应用价值。