质疑·追问:助力提升科学思维能力 ——以2023年湖南省物理高考压轴题为例

王小军 左 潘

(西北大学附属中学,陕西 西安 710075)

1 原题呈现

例题:(2023年湖南省高考第15题)如图1,质量为M的匀质凹槽放在光滑水平地面上,凹槽内有一个半椭圆形的光滑轨道,椭圆的半长轴和半短轴分别为a和b,长轴水平,短轴竖直．质量为m的小球,初始时刻从椭圆轨道长轴的右端点由静止开始下滑．以初始时刻椭圆中心的位置为坐标原点,在竖直平面内建立固定于地面的直角坐标系xOy,椭圆长轴位于x轴上.整个过程凹槽不翻转,重力加速度为g.

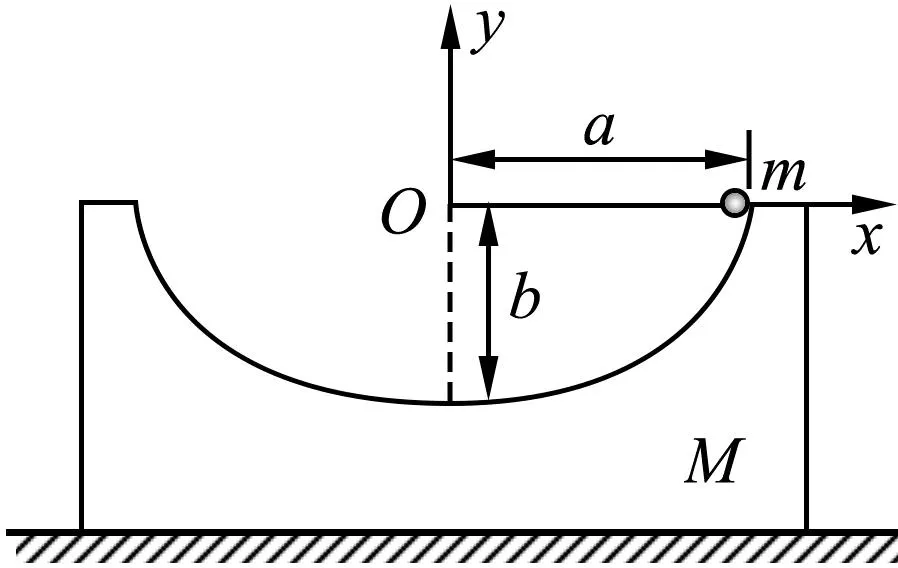
图1 原题图

(1) 小球第一次运动到轨道最低点时,求凹槽的速度大小以及凹槽相对于初始时刻运动的距离;

(2) 在平面直角坐标系xOy中,求出小球运动的轨迹方程;

2 分析追问

这道高考压轴题的设计很具有创新性,将经典的“球槽模型”中半圆形槽拓展为半椭圆形槽,摒弃了“重数学运算技巧,轻物理思维方法”的常规做法,让人眼前一亮.[1]

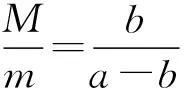
在正常地分析3个问题后,进一步追问小球在内有半椭圆形的光滑轨道的凹槽内运动,凹槽又处在光滑水平地面上,小球的运动轨迹与凹槽的质量有关系吗?小球运动速度如何变化?一直增加吗?小球运动到最低点对凹槽的压力多大?最低点是小球对凹槽压力最大位置吗?要想解决追问问题,通过常规惯性系方法分析问题将使问题变得复杂,如果以凹槽为参考系,即在非惯性系下分析解决问题,培养学生科学思维能力.

2.1 追问1:小球的运动轨迹是什么?

假设有两个相互平动的参考系S和S′.并且分别建立笛卡尔坐标系.S′参考系相对S参考系在x方向以恒定加速度aS′做加速运动.设空间中一个物体P发生运动,如图2所示.

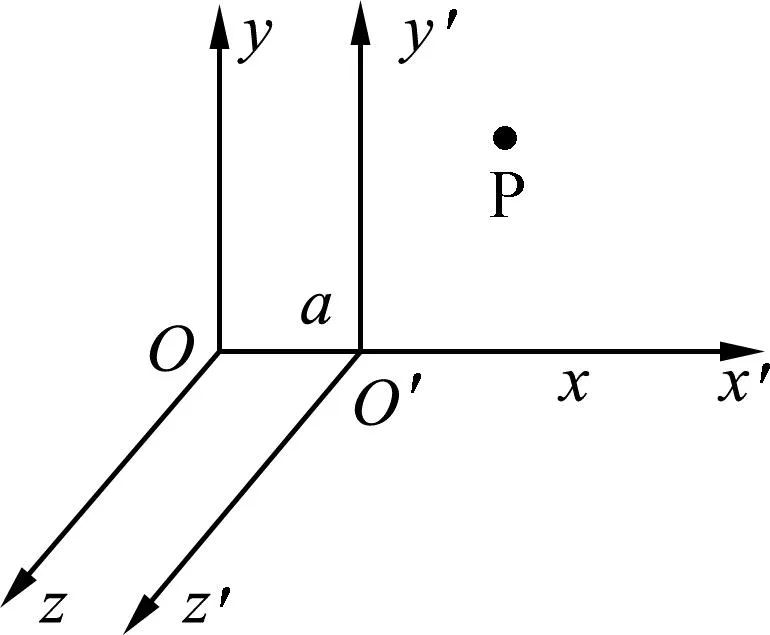
图2 物体在坐标系中的运动

位置关系

(1)

在非惯性参考系下研究对象会相对于惯性参考系向x轴反方向运动.

对式(1)求导可得速度关系

v′=v-vO′-aS′t.

(2)

在非惯性系下研究对象的任意时刻速度等于其在惯性系速度与S′参考系任意时刻速度之差.当t=0时表示初始时刻物体初速度等于

v0′=v-vO′=aSt-vO′.

(3)

对式(2)速度公式求导得

a′=a-aS′.

(4)

在非惯性参考系下研究对象加速度等于其在惯性参考系加速度与S′参考系下加速度差.并且研究对象运动规律依然满足运动学3个基本规律,故可以通过此3个描述运动的3个基本物理量在不同参考系下来研究物体的基本运动规律,对解题往往有更深入理解.

(5)

根据(1)式可知y惯=y非、x非=x惯-ΔxM惯,其中ΔxM惯为凹槽向右运动的距离.

根据惯性系下系统水平方向动量守恒有

mvm惯=MvM惯.

(6)

微元法可知∑mvm惯Δt=∑MvM惯Δt,即

mxm惯=MΔxM惯.

(7)

xm惯=a-x惯.

(8)

联立式(5)(7)(8)可知小球的轨迹方程为

(9)

其中-b≤y≤0.可见其运动轨迹仍然为椭圆解析表达式.

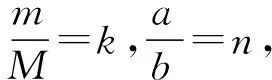
(10)

为了用MATLAB模拟小球的运动轨迹,令a=1.通过对k和n取不同的值来模拟小球的运动轨迹.

(1) 当凹槽的质量M≫m时,即k→0时,可观察小球的运动轨迹如图3所示.

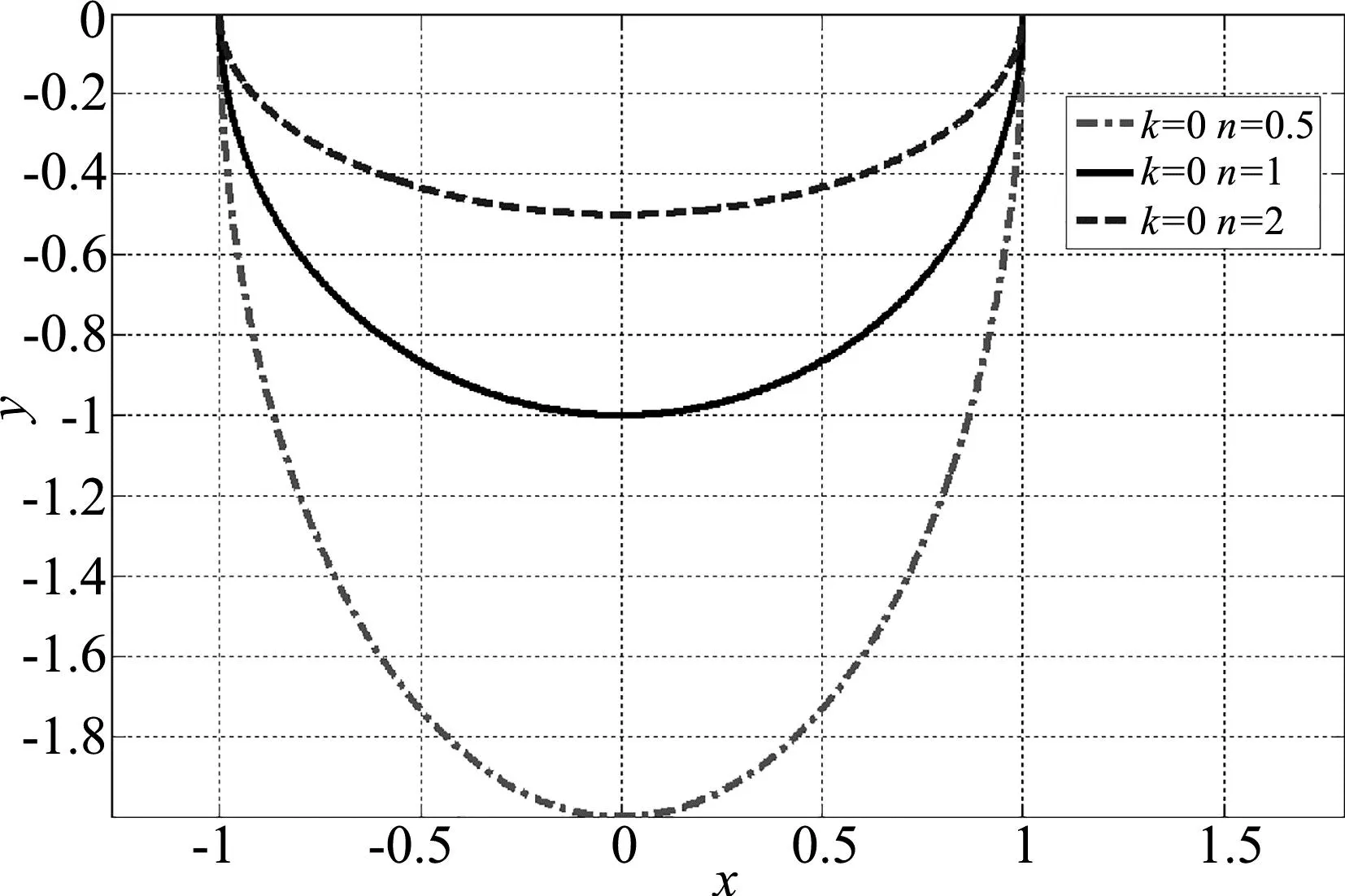
图3 小球运动轨迹(M≫m)

根据图3可知,当k→0时,对n赋予不同值,发现小球的运动轨迹和凹槽的弯曲程度保持一致;此时可认为小球在运动过程中凹槽一直不动,因此小球的运动轨迹与凹槽对应形状一致.

(2) 当小球的质量远远大于凹槽的质量时,即M≪m,此时k→∞,数值模拟小球的运动轨迹如图4所示.

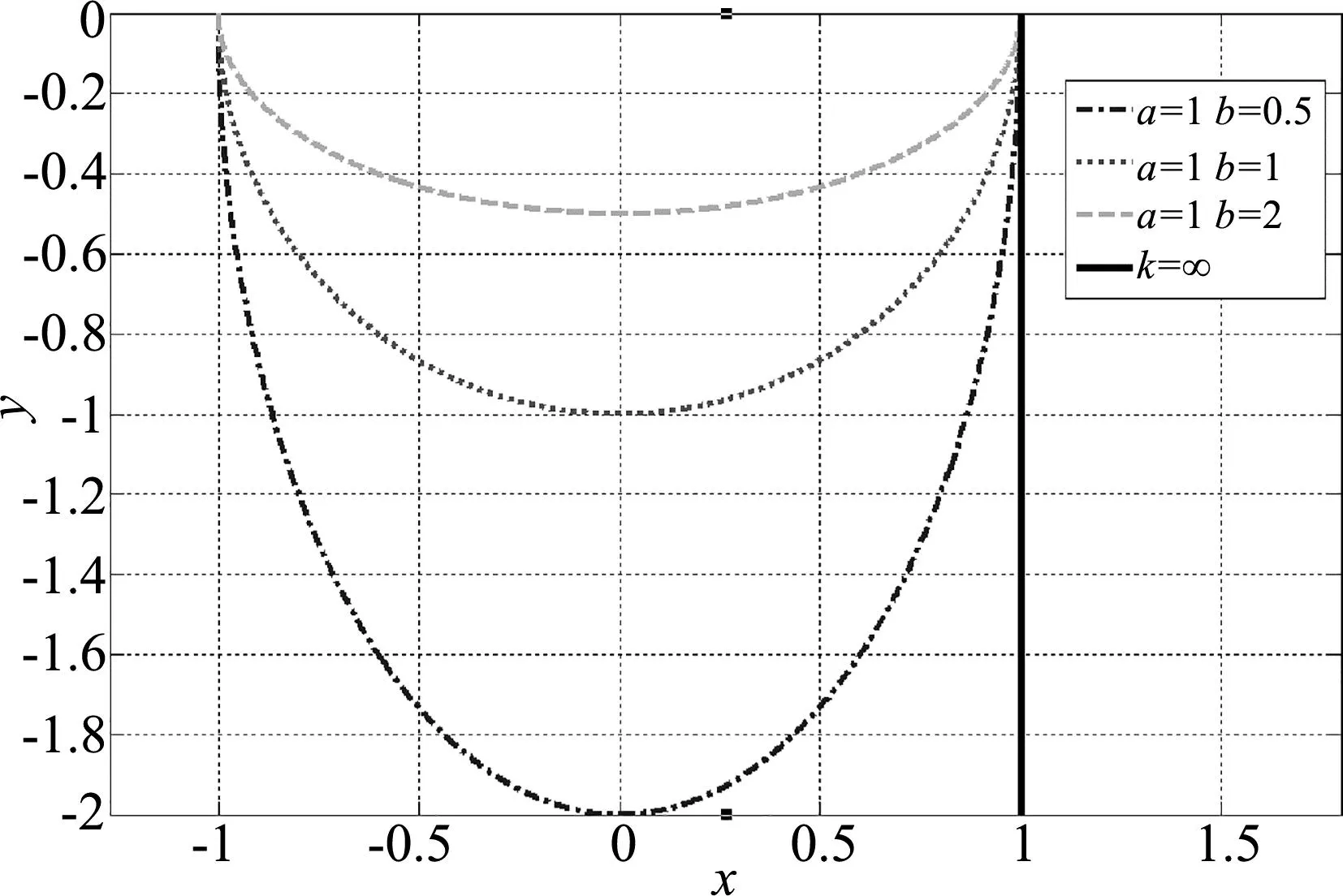
图4 小球运动轨迹(M≪m)

根据图4可知,首先通过MATLAB数值模拟对凹槽在参数n=0.5,n=1,n=2时别绘制凹槽曲线,在绘制k→∞时,对n赋予不同值,发现小球的运动轨迹为一直线;此时可认为小球在运动过程中凹槽水平速度大于小球的速度的水平分量,此时小球做自由落体运动.

(3) 当小球的质量与凹槽质量之比非特殊值时,本文分别数值模拟了当n=0.5、n=1、n=2时对k=0.5、k=1、k=2时MATLAB数值模拟情况如图5所示.

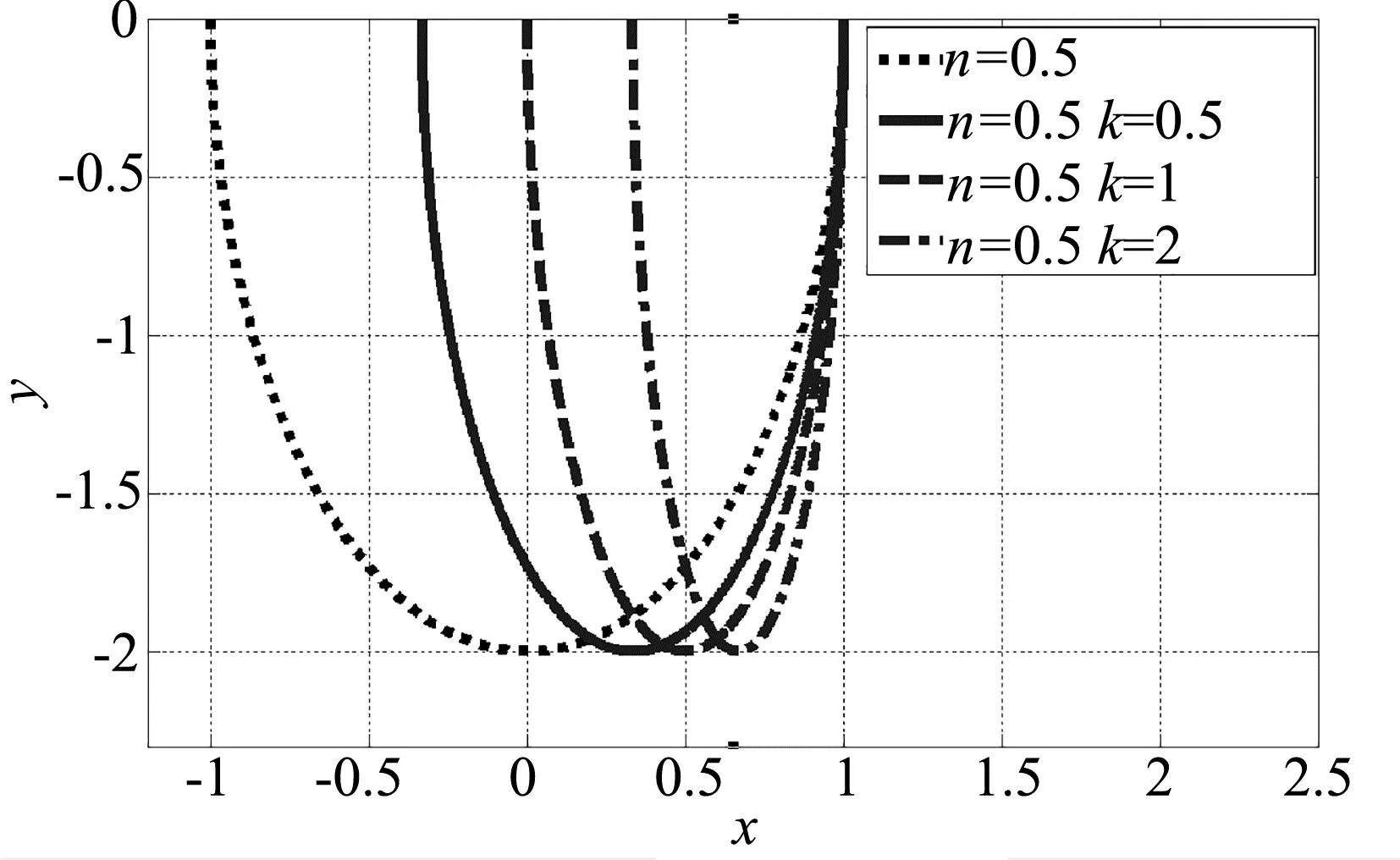
(a)

图5中最左侧虚线均反应凹槽实际曲线,其他线分别表示在不同参量下小球的实际运动轨迹.由图可知,当n恒定时,随着k值(小球质量与凹槽质量之比)的增加,小球的运动轨迹左移,其符合动量守恒定律求解人船模型的特征.图5(a)(c)变化趋势可以反映小球相对凹槽运动至左端点时凹槽向右运动位移.

2.2 追问2:小球运动速度如何变化?

如图6所示,如果凹槽长半轴和短半轴相等,即a=b时,此时凹槽可看作是半径为R的半圆形,能否求小球在下落过程中小球的速度、凹槽速度?

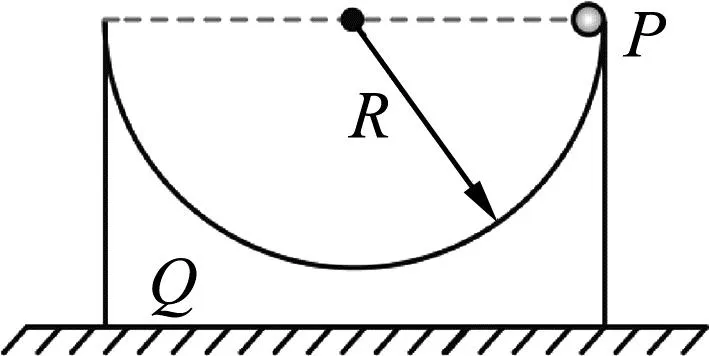
图6 小球在半圆槽中的运动

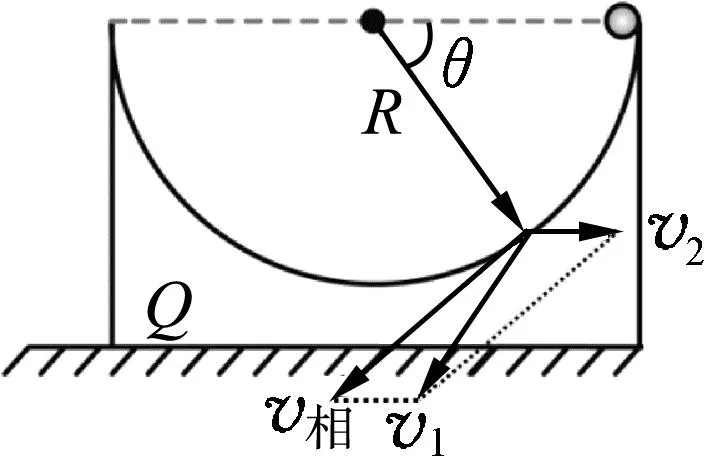
图7 小球运动速度分析

假设小球运动过程中相对于凹槽的速度为v相,小球对地速度为v1,凹槽对地速度为v2,小球下落过程中与凹槽圆心连线与水平面的夹角为θ,如图9所示.

小球在凹槽运动过程中,动量守恒,机械能守恒,其运动中满足关系式为

mv1x=Mv2.

(11)

(12)

v1x2+v1y2=v12.

(13)

v相sinθ-v2=v1x.

(14)

v相cosθ=v1y.

(15)

联立式(11)～(15)可知

(16)

(17)

(18)

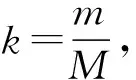
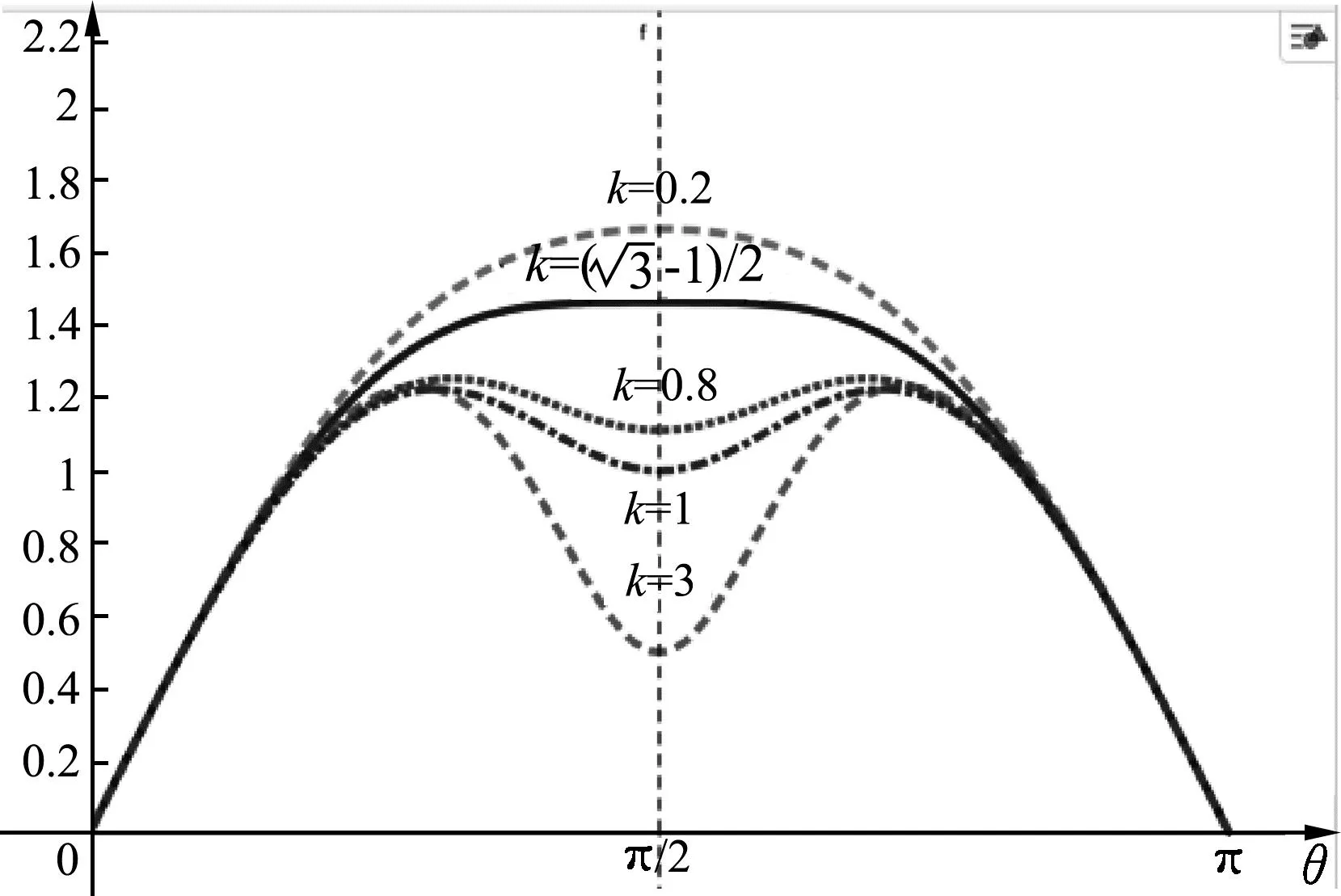
图8 数值模拟速度v1

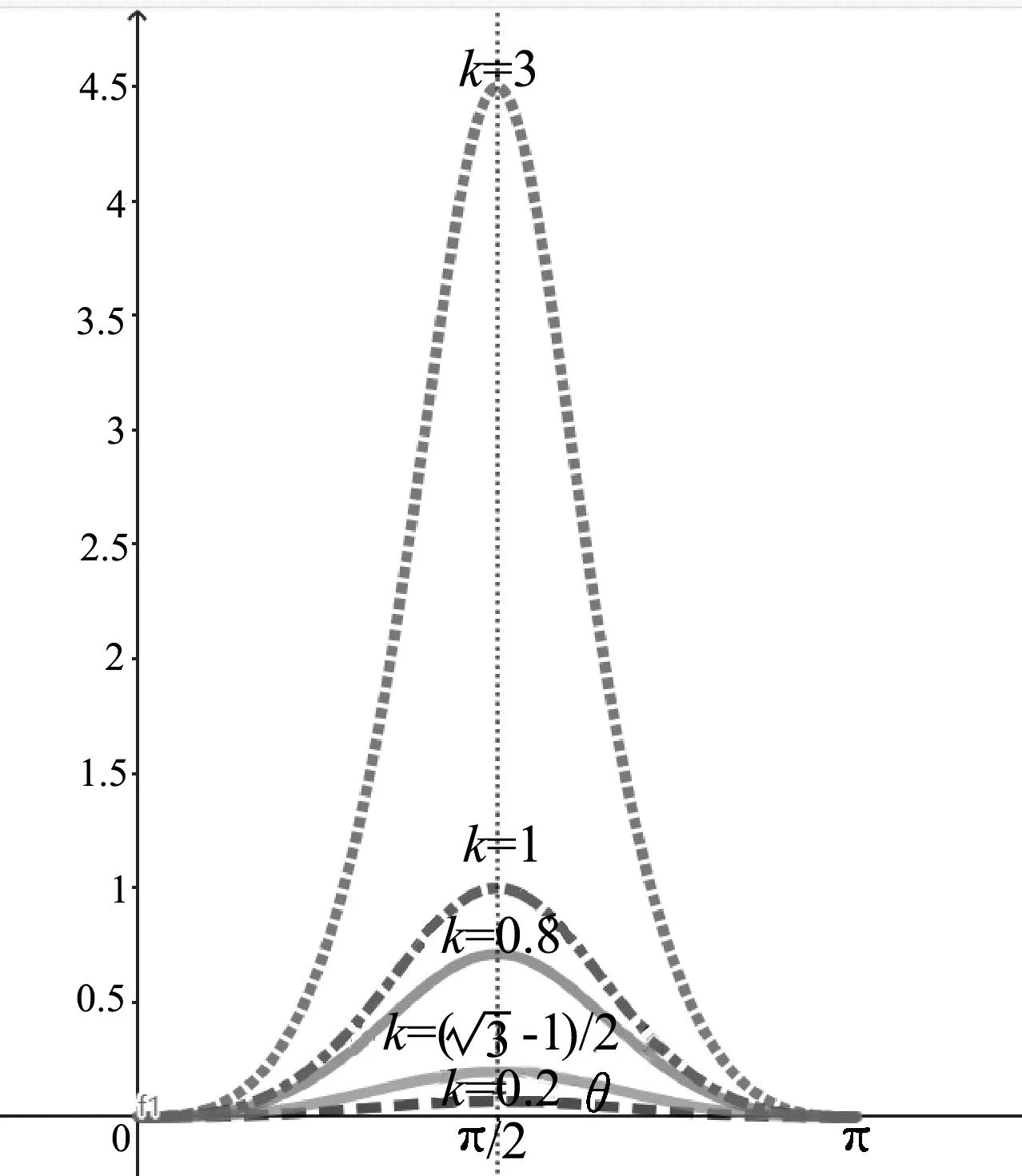
图9 数值模拟速度v2

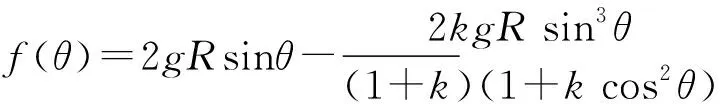
理论解释:当小球下降过程中系统机械能守恒,下降过程中弹力对凹槽做正功,所以凹槽速度增大,小球上升过程中弹力对凹槽做负功,所以凹槽速度减小;而小球下降过程中小球的重力势能减小,动能会无法判断.

2.3 追问3:小球运动到最低点对凹槽的压力多大?

分析:小球的运动为非惯性系分析,受力分析如图10所示.

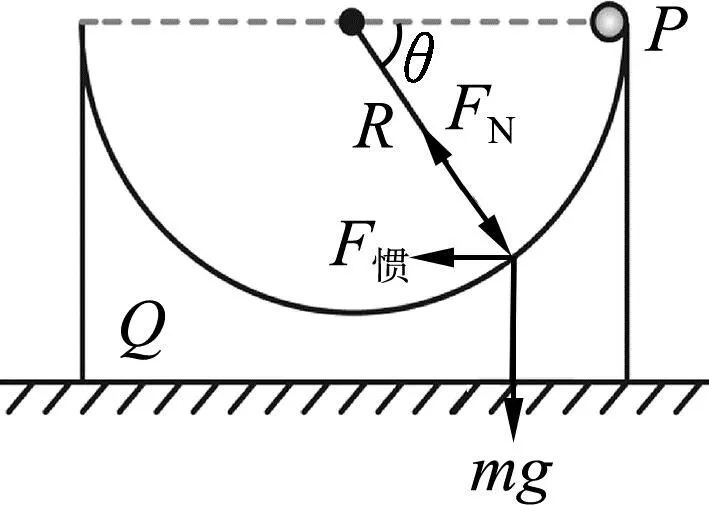
图10 小球受力分析图

(19)

F惯=maM.

(20)

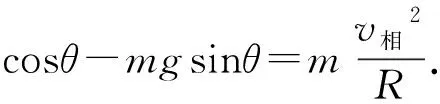
(21)

联立式(18)～(21)得

(22)

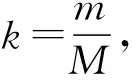
(23)

分析上式可知,当小球运动至凹槽最低点时,即θ=π/2时,可得

(24)

2.4 追问4:最低点是小球对凹槽压力最大位置吗?

为了解决这个问题,对式(23)压力变化数值模拟如下.

通过分析图11可知,当θ=π/2时,小球下降过程中对凹槽的压力最大.小球在最低点的压力随着k值的增加而增加.在0→π/2时,压力随着θ的增加而增加;在π/2→π时,压力随着θ的增加而减小.

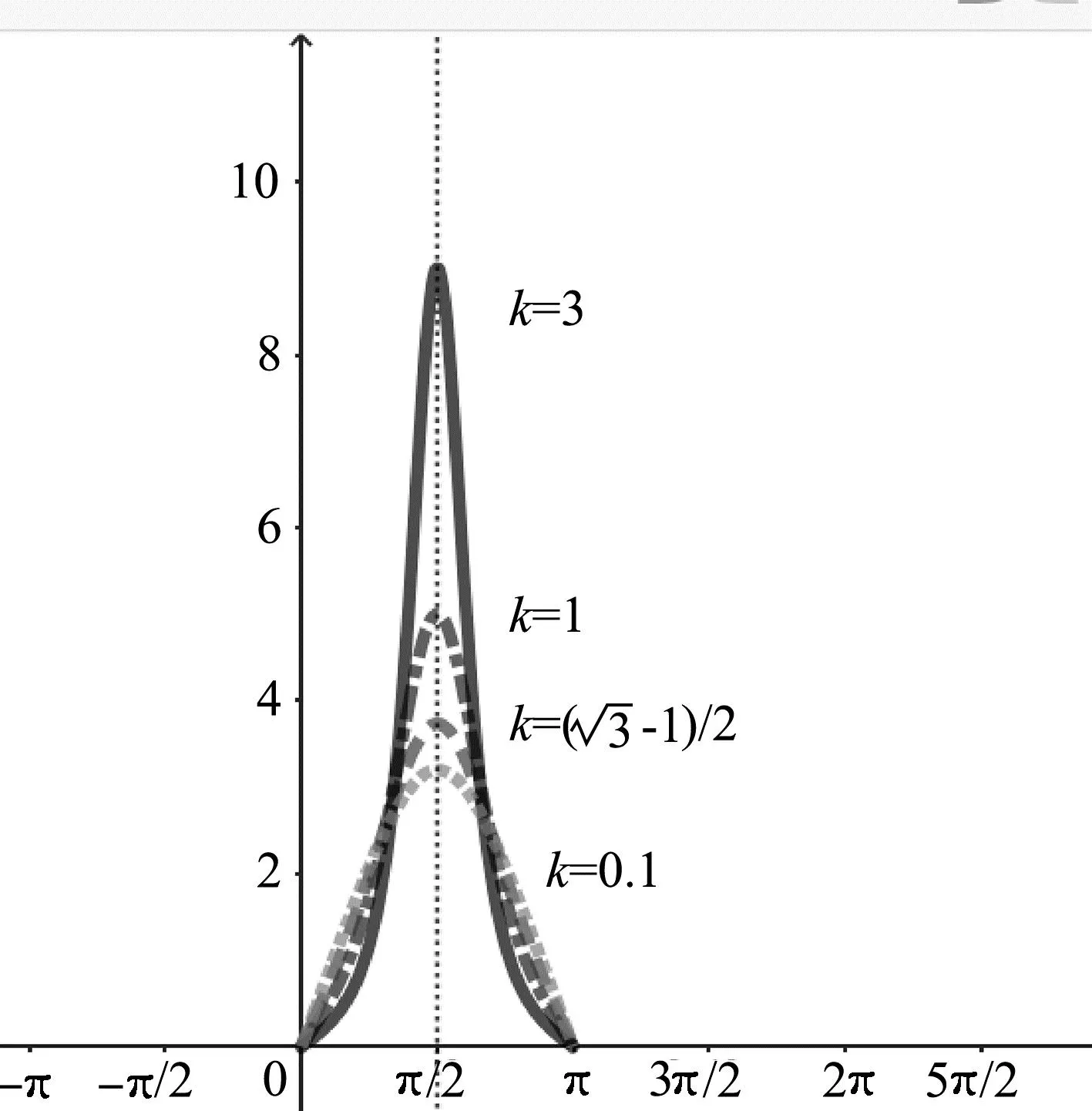
图11 压力变化数值模拟

2.5 追问5:最低点小球的对地速度v1不一定是最大值,为什么对凹槽压力最大?

实际上,在非惯性系下小球对轨道的压力决定速度是v相,v相与凹槽的速度v2的矢量和才是v1.而v相变化趋势决定了小球压力变化情况.所以不能单纯根据v1的变化趋势直接说明小球对轨道的压力情况;根据式(18)可知当θ=π/2时,小球在最低点的相对速度为v相2=2gR(1+k).因此可以解释在最低点时,压力峰值随着k值的增加而增加.

3 教学启示

3.1 转变角色拓展试题

在复习备考中教师不能单纯地充当“讲题者”,学生不能机械地充当“刷题者”,在习题教学中,要让学生从题海中跳出来,不背题,不刷题,[2]教师要摒弃传统的就题论题的方式,而是从命题者角度依据高考评价体系及课程标准对高考典型试题进行深度挖掘、解析和拓展,提升物理思维品质.

3.2 创新方式数形结合

《普通高中物理课程标准(2017年版2020年修订)》指出“积极探索信息技术与物理教学的深度融合”,[3]教师要运用一切可能的图示、动画、声音、视频和实验等技术手段对教学环节进行设计和整合,[4]积极探索和利用信息手段对问题进行模拟展示,培养学生从不同角度思考问题,不同方式解决问题,提升物理思维创新性.

3.3 质疑追问提升素养

“科学思维”主要包括模型建构、科学推理、科学论证、质疑创新4个要素.无论是新课教学还是复习备考,教师要有意识地创设质疑环境,主动提出引发疑问的思维问题,认真对待学生提出的异想天开的问题,[5]新高考复习不能再被动地“以不变应万变”,而应主动地“以善变应多变”,[6]捕捉学生质疑火花,引导学生分析题目深层次的物理过程,让学生知其然更知其所以然,[7]激发学生质疑意识,提升学生质疑能力,享受师生质疑追问解决问题过程的快乐.