中间法三角高程测量代替水准测量的可行性分析

雷力军，王志文

（中交第一航务工程勘察设计院有限公司，天津300222）

引言

高程测量是工程测量中的重要一环，在施工放样、变形监测、地基勘察等项目中往往涉及到高程测量，已是测绘者必须掌握的测绘技能之一。目前高程测量主要采用的方法为水准测量[1]，该方法测定的高程精度最佳，是精密工程测量、高级控制网普遍采用的方法。但水准测量也有突出的缺点，水准测量的工作量大、参与人员多、成本高、测量耗时长、测量工作进展十分缓慢，特别在高地、山区等地表起伏比较大的地区显得尤为突出，因此寻找出一种灵活、便捷、成本低、受地形限制少的高程测量手段，一直是测量领域研究的热点、难点[2]。

三角高程测量具有水准测量无法企及的优点，它具有测量速度快、耗时短、方便灵活、视线长、小成本、减小系统误差累计、受地形影响小等优 势[3-5]。因此研究分析三角高程测量能够达到怎样的精度水平以及在什么条件下可以取代水准测量，这些问题这在实际工作中显得尤为突出，是我们测量工作者必须攻克的难点。

1 中间法三角高程测量原理和误差改正

1.1 中间法三角高程测量原理

三角高程测量在以前就被提出，但由于当时的测量技术落后，测量仪器的测角、测距误差很大，因此该方法没被重视。随着测绘技术的发展，测量仪器越来越精密、精度越来越高尤其是测角、测距精度有了长足提升，这使得三角高程测量技术成为了可能，在测量精度方面能够达到水准测量水平[6-8]。此外，三角高程测量灵活、方便、高效、受地形限制少的特点，使得三角高程方法具有广阔的推广前景以及市场价值，其测量原理图如下[9]。

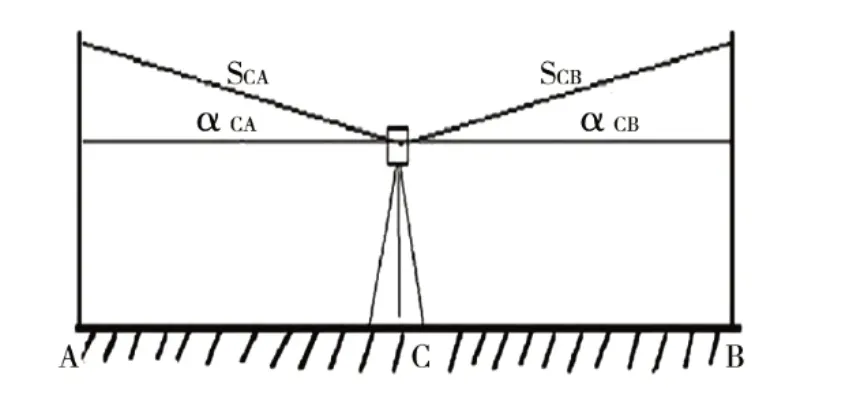
图1 中间法三角高程测量示意图Fig.1 Principles of elevation survey by Trigonometric Leveling using midway-method

假设在地面上存在两点A 和B，将全站仪架设在AB 中间位置C 点，在A、B 两点安装觇标。使用全站仪照准B 点的觇标，测量出垂直角αCB、CB两点之间的斜距测量值SCB、全站仪高i和B 点觇标高vB，然后再使用全站仪照准A 点的觇标，测量出垂直角αCA以及CA 之间的斜距测量值SCA和A点觇标高vA。则通过几何计算可以分别得到CB 和CA 之间的高差值：

由上述两式可得A、B 两点之间的高差：

若是在A、B 两点上的觇标高度一致，公式（3）可以进化成如下：

由公式（4）可知，测量结果消除了全站仪高i和A、B 点觇标高v对高差测量有影响，提高了观测精度。

1.2 球气差改正

1）球气差改正原理

三角高程测量一般把水准面看作平面，把视线作为直线。然而大地水准面是曲面而不是直线，因此地球曲率必然会给高差测量造成误差尤其两观测点之间的距离比较远时，该误差尤为突出。当光线通过密度不一致的空气时，光线不会在沿直线传播而会发生折射，也就是从仪器出发的光线到目标点之间的路线不是直线，而是一条既有曲率又有挠率的复杂空间曲线[1,2]，地球曲率和大气折射的影响原理如图2 所示。

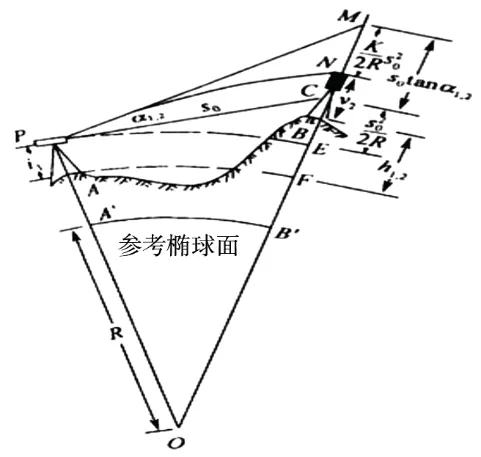
图2 地球曲率和大气折光的影响原理图Fig.2 Principle of the influence of Earth curvature and atmospheric refraction

如图2 所示，假设地面上存在两点A 和B，把全站仪架设在A 点，量取仪器高为i1；在B 点架设砚标，并测量砚标高度v2；然后使用全站仪照准砚标获取水平距离S0。

图2 中，PC 线段代表全站仪所提供的水平视线；PN 曲线代表光线从全站仪望远镜出发到目标点的传播路径；PM 代表的是过点P 的曲线PN 的切线；PE、AF 曲线分别代表过P 点和A 点的水准面；R 代表的是参考椭球面的曲率半径。

当架设在A 点的全站仪，其望远镜照准的方向与线段PM 重合时，由于光线受到大气折射的影响，其传播路径并不会沿着线段PM 而是会沿着曲线PN 传播，此时的N 点正好会落在望远镜的横丝上，换言之，架设在A 点的全站仪所测的垂直角为P 点与M 点之间的垂直角为α12。

由图2 可明确的计算出地面两点A、B 之间的高差的计算公式：

在公式（5）中，EF代表的是全站仪仪器高i1；NB代表的是砚标高度v2；CE代表地球曲率对高差影响的改正值；MN代表大气折射对高差测量的影响改正值；

地球曲率和大气折光对测量的影响改正值的影响改正计算公式如下：

公式（7）中的R′表示的是曲线PN在点N处的曲率半径。在此，设(K 表示大气折光系数)，因此可以得到：

在进行三角高程测量时，由于点A 和B 之间的距离一般不会很长，因此，AB 之间的水平距离S0与曲率半径之间的比值比较小，因此可以认为PC垂直OM，换言之，∠PCM≈90°。所以三角形ΔPCM可以认为是直角三角形，因此公式（5）中的MC可以表达如下：

公式（11）中S0表示的是高斯平面上的水平距离，当测量仪器测量的距离为斜距S 时，其高差计算公式为：

2）球气差对测高的影响值

由公式（12）可知，球气差对测量高差的影响除了受到测距的影响之外，还会受到垂直角的影响。为了获知当球气差对测量高程的影响程度，本文计算了球气差改正值随着测距长度和垂直角变化的变化值，由图3 所示。在计算过程中，取大气折射系数取值为0.12。

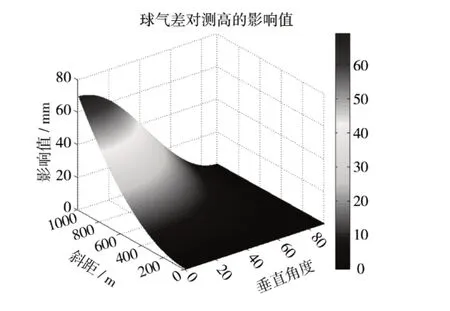
图3 球气差对测量高程的影响值Fig.3 The influence value of Refraction abnormity on measuring elevation

从图3 可以明显的看出，当斜距一定时，球气差对测量高差的影响随着垂直角的增加而减小。当垂直角一定时，球气差对测量高差的影响随着斜距的增加而增大。当斜距小于100 m 时，地球曲率对测量高差的影响不受垂直角的影响，当垂直角大于85 °时（斜距小于1 000 m），此时地球曲率对测量高差的影响可以忽略不计。

2 中间法三角高程测量精度分析

2.1 中间法三角高程测量中误差求解

由上述公式可知中间法三角高程测量的计算公式如下：

如果两棱镜高的高度相同，则公式（13）则可进一步得：

公式（15）中，α1、α2表示前视后视的垂直角；S1、S2表示前视后视的斜距；忽略其中的微小项可得如下：

佛性是佛教理论中的基本观念，这一观念无论在印度佛教还是中国佛教发展史上都具有重要影响。诸多佛教经典都有过对佛性的相关论述，也有不少佛教流派或宗派对佛性做出过种种解释。佛性含义十分丰富，内容也极为复杂，本文所指佛性为大乘佛教中普遍接受的思想，基于大乘佛教佛性论中一切众生皆有佛性，一切众生皆可成佛的观点，在成佛之路以及由佛性引发的现世价值方面做一基本阐述。

由公式（16）中可以看到S1∙cosα1以 及S2∙cosα2，该两个变量分别表示前后视距的平距，为了简化误差分析的复杂性，以平距来表示测距误差，则公式（16）可改为如下所示：

由公式（17）可以得知：在进行中间法三角高程测量时误差来源分为平距测量、竖直角测量和K值的误差，它们对高差的影响分别如下：

2.2 中间法三角高程测量中误差的变化情况

为探索中间法三角高程测量中误差的变化情况以及其能够达到怎样的精度水平。现取两倍的中误差作为极限误差，也就是 Δ限=2mh，与有关规范中规定的三、四等水准测量限差进行比较。在实际应用中由于视线等问题，测量时前后两棱镜高度不可能一直保持相同，故首先考虑前后两棱镜高度不一致的情况，根据公式（13），由误差传播定理可得：

此时的中间法三角高程测量中误差平方中包含测角中误差、测距中误差以及大气折射中误差和棱镜测高误差，因此影响中间法三角高程测量中误差的因素有：测距、测角、大气折射和棱镜测高。

就目前常规的全站仪精度而言，其测距精度一般为±（1+1× 10-6D）～（5+5× 10-6D），其中D 表示测距长度（单位：km），而测角精度一般为±0.5”～6.0”。对于全站仪高以及棱镜高的量取，一般采用卡尺进行测量，当要求的精度比较高时，可以采用测杆量取。大气折射系数K 的误差一般在±0.03～0.05 之间。在本论文中选取全站仪的测距精度为±（2+2× 10-6D）、测角精度为2”、大气折射系数误差为±0.04、仪器高和目标高的测量误差为±2 mm，以这些指标进行本文论的理论研究。

现取两倍的中误差作为极限误差，Δ限=2mh，与三、四等水准测量限差比较。

由表1 可以看出：中间法三角高程测量的中误差受到测距、测角的影响，当测距越小、垂直角越小，则中间法三角高程测量精度越高。因此，为了提高测高精度，在进行中间法三角高程测量时尽量缩短测距和测角。由表1 可以看出，测距在800 m以内时，中间法三角高程测量可以满足四等水准测量限差要求。

表1 中间法三角高程测量极限误差与三、四等水准测量限差对比Tab.1 Comparison of the Limit Errors of Intermediate Trigonometric Elevation Measurement with the Limit Errors of Third and Fourth Leveling Measurement

由表1 中的结果也可以看出，当测距一定时，测距中误差对测量中误差的影响随着垂直角的增加而增加，而当垂直角一定的时，测距中误差对测量中误差的影响随着测距的增加而增加。

3 工程实例应用

我公司于2022 年承担了北方某港口泊位及航道水深测量项目，项目中临时验潮站高程需从附近高程控制点（A 点）进行引测，但在进行验潮站高程引测之前，需对A 点的稳定性进行检测，距离A点最近的另一个高程控制点（B 点）相距为4.5 km。AB 高程控制点间有半岛山地、地形高差起伏较大，又需经过回填区域，回填区内常有沟沟坎坎的复杂地形，采用常规水准测量方法进行高程控制点检测势必费时费力，为加快工期进度及节约人力、物力等各项生产成本，本项目高程控制点检测采用中间法三角高程测量方法进行。

使用徕卡TCA 2003 全站仪进行测量，其精度指标如下：

测角精度：±0.5″；

测距精度：±(1+1× 10-6D) mm；

D 代表距离单位为km，具有目标自动照准功能。

在进行中间法三角高程测量时，尽量把全站仪架设在两测点中间，采用两个观测测回，即(盘左)– 前(盘左) -前(盘右)– 后(盘右)的测量程序。为减小外界环境对测量结果的影响，选取下午2 h 至4 h进行数据采集，这个时间段观测条件比较稳定，可以提高数据采集的质量，减小测量误差，高差检测统计表见表2。

表2 高差检测统计表Tab.2 Statistical table for height difference detection

由表2 数据可知高程控制点稳定，可作为高程起算点使用。同时验证了中间法三角高程测量可在实际工程中能代替四等水准测量，满足日常测量需要。

4 结语

本文分析了中间法三角高程的基本原理、误差来源和改正模型。在理论证明了其测量精度可达四等水准测量，并通过具体实际工程应用验证了中间法三角高程测量的可行性，可满足日常测量工作需要。