借游戏情境之桥,行单元复习之路——以“不等式与不等式组”单元整体复习课为例

⦿ 江苏省盐城市大丰区实验初级中学 董德荣

单元整体复习课就是在某一单元学习结束之后,通过系统整理与练习深化知识理解,促成完整知识体系,促进巩固、拓展、深化和提升的一种课型,是初中数学教学中的重要课型之一.因此,如何提高单元复习课的效果是摆在一线数学教师面前的一个重要话题.从教育视角来看,游戏具有本体性和工具性价值,不仅可以让学生感受到快乐与自由,还能让学生理解数学知识,获取思想方法启迪,发展数学思维等.倘若数学单元整体复习中,教师能借用“游戏情境”构建教学实践,不仅可以促进学生的主动建构,还能让单元整体复习课教学绽放独特魅力.

1 复习设想

为了让单元整体复习课更加有效,笔者进行了单元整体复习课教学的尝试.下面以“不等式与不等式组”的单元整体复习课教学为例具体阐述,以实现高效复习.在新课学习时,学生系统学习了本单元涉及的所有知识点,也熟悉了用数轴表示一元一次不等式解集的方法,但通过建立不等式模型解决实际问题则需要教师在单元整体复习中给予一定的方法指导.那么,本节课中除去落实巩固与深化一元一次不等式(组)的解法的目标,更需要解决上述问题,助力学生自主获得解决此类问题的思想方法和活动经验.

2 复习过程

环节1：游戏导入,快速入课.

活动1：如图1,电脑屏上A方框内有数式a+3,B方框内有数式6a-2.每点击一次鼠标的“开始”按钮,A方框内的数式则会随之加a,B方框内的数式则会随之加1,且均呈现化简后的结果.

图1

师:这个游戏有意思吗?事实上,不必操作我就能准确知晓点击五次按钮后的情形,即两个方框内数式相同,你们相信吗?下面开始验证!(学生迫不及待地开始游戏,并记录每一次操作后方框内的数式,如表1,果然教师的猜测是正确的.)

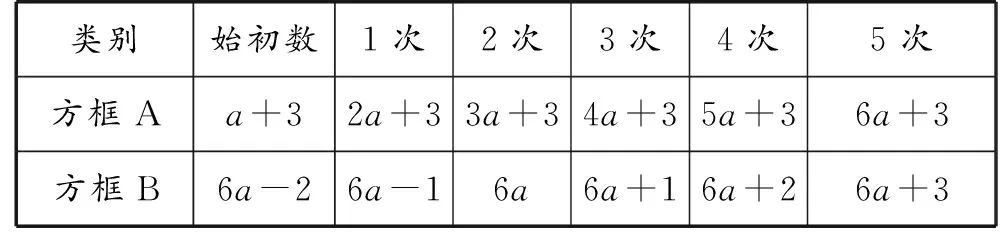
表1 前5次操作后方框内的数式

评析：对学生而言,最好的老师就是“兴趣”,以游戏为载体引入课堂,能将学生的学习积极性快速调动起来,能够将学生的知识储备快速聚集起来.尤其是此处教师的神秘猜测,充分点燃了学生的参与欲望,从而迫不及待地投入到预测的验证中去.当运算结果揭晓之时,学生自然而然就掌握了根据游戏规律列出代数式的方法,从而为后续的复习储备了充分的知识能源.

环节2：问题引探,渐入佳境.

活动2：“数式游戏”继续下去,再次点击5次“开始”按钮,仍然记录两个方框内的数式,10次操作后两个方框内的数式哪个大?(学生又一次投入游戏,并生成了表2所示的数.)

表2 前10次操作后方框内的数式

生1:A,B方框内的数式分别是11a+3和6a+8,但是该如何比较这两个数式的大小呢?(其余学生有的小声讨论,有的陷入沉思.)

师(追问):一般来说,我们怎么比较两个数的大小?(学生回顾并阐述多种方法.)

师:那此时该选择什么方法呢?

生2:我会选择作差法,即(11a+3)-(6a+8)=11a+3-6a-8=5a-5=5(a-1).当a>1时,A方框内的数比B方框内的数大;当a=1时,A方框内的数与B方框内的数相等;当a<1时,A方框内的数比B方框内的数小.

评析：以活动2为载体,引出比较两个数大小的问题,让学生在回顾不等式的性质与解法中,借助分类讨论得出结果.这一环节中,教师不失时机的追问,让学生自然而然地回顾旧知,整合并提炼解决问题的策略,同时切实感悟分类讨论思想.

环节3：问题深入,深化认知.

活动3：基于游戏的规则,是否存在一个实数a,可以使第5次点击按钮后,每次点击按钮A方框内的数都比B方框内的数大?若存在,试写出满足条件的所有a值,并用数轴予以表示;若不存在,试说明原因.(活动3具有一定的难度,为了分化核心活动的难点,教师以“问题串”为主线深化复习.)

问题1第n次操作后,A方框内的数是多少?B方框呢?

问题2根据条件“第5次点击按钮后,每次点击按钮A方框内的数都比B方框内的数大”,可列出什么不等式?

问题3若将n视为已知数,该如何求解上述不等式?

评析：在这一环节中,不等式的性质与解一元一次不等式的方法与步骤得到了极好的整合与提炼,更重要的是让学生在轻松愉悦的环节中促进了数学建模能力的发展.

环节4：拓展游戏,发展素养.

活动4：基于游戏的规则,是否存在这样一个数a,可以使每一次点击按钮后A方框内的数加上B方框内的数的一半的和不小于0,且A方框内的数的6倍与B方框内的数的差不大于20?若存在,试写出a的取值范围;若不存在,试说明原因.(同样地,教师依旧以“问题串”的形式化解难点.)

问题1尝试以代数式表示“A方框内的数加上B方框内的数的一半的和”及“A方框内的数的6倍与B方框内的数的差”.

问题2你会表示“不小于”及“不大于”吗?

问题3根据题设你能列出什么不等式组?

问题4若将n视为已知数,问题3中生成的两个不等式分别该如何求解?

问题5你会在数轴上分别表示出这两个不等式的解集吗?那原不等式组的解集又是什么?

评析：在这一环节,借助新的游戏情境,可有效实现拓展提升的目标,促成学生对不等式组的深刻认识.

3 些许感悟

游戏是学生心理发展的内在需求,更是学生智力发展的有效手段.单元复习课中借助游戏情境发掘学生的思维与创造,最终在数学与游戏的完美沟通下,使学生的学习达到精神与享乐的并重,目标与方法的统一[1].

3.1 关照学习经验,引发复习兴趣

数学活动的设计一旦脱离学生的认知基础,一切活动的开展都将是徒劳的.因此,课前需分析学生的认知水平,探寻到本节课的出发点、生长点和生成点,让游戏准确地切入学生的最近发展区,让巩固知识、体验学习、发展思维得以落实,同时搭建从感性走向理性的桥梁.本课采用“数式游戏”导入,让学生在游戏中自主复习列一元一次不等式(组)、解一元一次不等式(组)、在数轴上表示一元一次不等式(组)的解集等知识.学生在“玩数学”的过程中丰富了感知,深化了认知,发展了思维,提升了素养,实现了快乐学习.

3.2 凸显复习目标,引领主动探索

数学教学需要以活动的形式引导学生主动探索,让学生被数学学习深深吸引,从而产生积极的学习样态.游戏情境下的单元整体复习课,不仅可以刺激学生积极的学习心理,还能让单元复习目标得以圆满完成[2].对于本节课而言,教师将“不等式与不等式组”的相关内容置于游戏之中,完成了从游戏到数学复习的自然过渡,在富有挑战性、综合性的四个游戏活动中,学生自主自发地建立代数式模型、列和解含有字母系数的不等式(组),在不知不觉中灵活地运用本单元所学知识和方法,感悟化归与建模思想,从而水到渠成地达成复习目标.更为关键的是,游戏中的智慧元素让学生的数学探索更加深入,让学生的数学思维更加灵动.

总之,游戏情境下的数学单元整体复习课,就是让学生在感知“数学好玩”的前提下“玩好数学”,从而提升单元整体复习课的教学效率.教师通过游戏情境这一桥梁,让单元整体复习更优质高效,同时引领学生走进数学,快乐复习.