创新使用教材 引领深度思维 提高数学素养

⦿ 江苏省苏州市工业园区青剑湖实验中学 赵三洪

教材是课程标准的载体,是课程理念实践的引领,是教师教学的依据.作为一线教师,我们需要具备创新使用教材的意识,通过创造性使用教材引领学生深度思维,以提高学生数学素养[1].下面,笔者从“直线与圆的位置关系”一课的教材实践谈起,提出创新使用教材的实践与思考.

1 课前慎思

对于本课的教学,笔者执教过数次,也听过多次公开课,基本上都是如下大同小异的教学思路:首先,由日出导入自然引出课题,促进学生感性认识的形成;接着从公共点个数出发探索直线与圆的三种位置关系,让学生经历数学抽象的过程;再结合图形直接生成圆心到直线的距离与半径的数量关系,使学生在数形结合中达成共识;最后通过例习题进行课堂运用,以深化学生的认识.然这样的一般教学模式的开展下,是否缺失了一些什么?深度解读教材是探寻答案的关键,于是,笔者在课前深入研究教材后,发现应着重强调类比点与圆的位置关系,为什么如此设计?直线与圆的位置关系为什么只有三种?为什么要比较圆心到直线的距离与半径这两个数量的关系?深度剖析上述问题之后,笔者对教学实践有了新的想法.

2 教学过程

环节1：以旧引新,激活思维.

问题1回顾之前点与圆位置关系的探究历程并思考:你是从哪些方面着手探究,得出了什么结论?请在独立思考或同桌二人交流后填写表1.

表1 点与圆的位置关系研究过程

学生活动:学生回顾“点与圆的位置关系”,有的独立思考,有的两人交流,流畅地回忆出了研究的过程,并完善表格后生成了表2所示的数据.

表2 点与圆的位置关系研究过程

问题2现用“直线”替换“点”,你觉得直线与圆的位置关系又是什么样的呢?(呈现课题.)

问题3现需要设计一份研究直线与圆的位置关系的方案,你打算如何设计?请将你的想法呈现在导学单上.

学生活动:学生在思考与探索后,自然而然地类比“点与圆的位置关系”,从多个方面展开探索,并将想法与观点呈现在导学单上.

设计说明：新旧知识相互沟通的过程对于学生而言就是具有意义的学习过程.从数学知识的逻辑性着手创设以旧引新的情境,为学生搭建类比学习的“支架”,可以让学生在体验新旧知识的内在联系中快速入课、深度学习.这样的情境创设是教师智慧的表现.在这一环节中,教师从上位知识着手引导学生回顾旧知,并以类比的方法研究“直线与圆的位置关系”的方法与思想,让学生在思考、探索和交流中切实感受类比学习法的妙处,实现高效建构.

环节2：开发教材,发展思维.

问题4直线与圆的位置关系有哪几种?请试着用图形表示,具体阐述分类的依据.

学生活动:学生在深度思考后能流畅画出3种图形,并总结出分类的依据为“直线与圆公共点的个数”,即图1所示的没有公共点、一个公共点和两个公共点这三种情况.

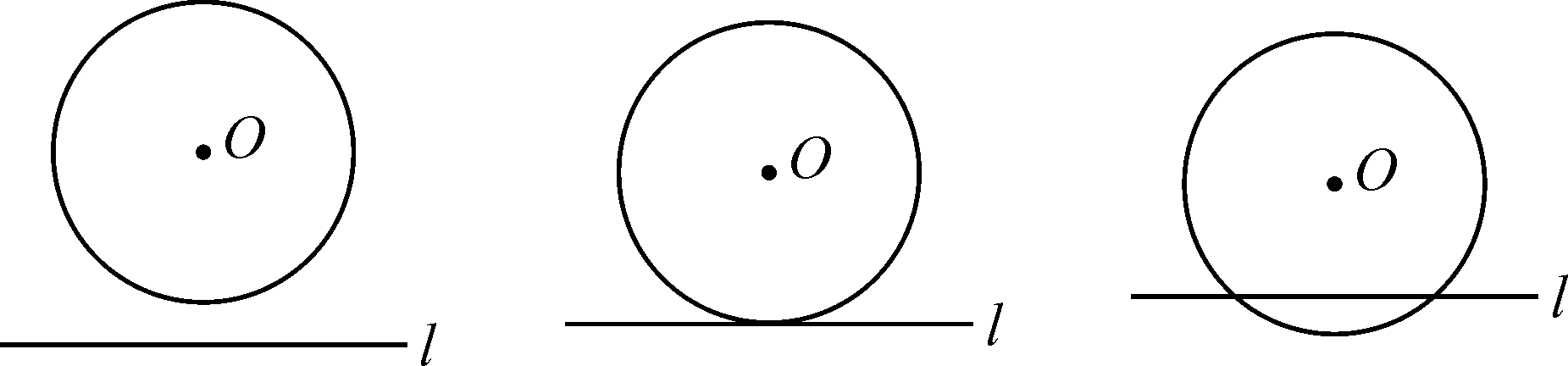
图1

追问1:只有这三种情况吗?为什么不存在三个公共点的情形?

追问2:基于运动的角度,这样的分类是否不重不漏?

学生活动:对于教师在直觉思维基础上的追问,学生易陷入困顿,无法给出说明只有三种情况的具体方法.进一步地,教师以追问2启发学生的深度思维,学生很快生成了“平移直线或圆”的方法,最终达成了共识.

设计说明：想要让学生在深度思考中发展思维,就需要教师在理解教材的基础上进行教材的开发.研读教材不难发现,教材中是通过平移发现直线与圆的公共点的.教师则需要基于教材意图和具体学情设计问题,让学生在利用平移检验直线与圆的位置关系中经历对认知误区的争辩,感受直线与圆的位置关系确实只有三种情况,为后续直线与圆的位置关系的定义打下伏笔.在这一过程中,学生经历了对知识发生和发展过程的领悟,使得思维水到渠成地得到了发展.

环节3：深挖教材,深化思维.

问题5这里选择比较垂线段和半径长度的原因是什么?(学生陷入思考.)

生1:因为垂线段最短.

师:很好,那我们再来观察这条垂线段,有何特征?

生2:它有两个端点,分别是圆心和垂足.

师:不错,那垂足又有何特征?

生3:距圆心最近.

师:是不是可以这样认为,直线上找到的距圆心最近的这个特殊点,就是所画垂线段的垂足,即可将直线与圆的位置关系转换为……

生4:垂足与圆的位置关系.

师:很棒!那这个垂足可以代表直线吗?

…………

设计说明：依照一般的设计思路,这一环节应继续类比点与圆的位置关系,抽象得出刻画直线与圆相应位置关系的数量,尽管这样的抽象方式较为自然,但部分学生在理解上还是会存在一些困难.因此,用平移直线的方式引领学生深度思维是十分可行的.针对学生需要深入体会数形结合这一现实,笔者用问题串驱动学生深度理解.这样的过程,教师没有在学生生成结论后展开练习,而是以问题串的方式让学生既经历了知识的学习,又经历了方法的操作,同时还经历了数学思想的体验,使学生的思维在深度锻炼中得以深化.

3 教后思考

3.1 深度解读是创新运用教材的前提

一般来说,教材由于自身的简约性等因素,会简化或舍弃一些内容,而这些“无字处”可以为学生的深度思考“留白”[2].因此,教师需深度解读教材,研究编写者的意图,让隐性的方法过程与显性的知识结果共同呈现,这样才能既有知识间的联系又有数学思想的感悟,既有知识技能的运用又有数学素养的发展.本课中无论是从认知结构角度创设的有效情境,还是基于定义设计的操作活动,又或是基于位置关系设计的问题串,都是在深度解读教材之后的创意想法,是在深度解读教材后的开发与拓展,都推动了学生的深度思维,促进了学生数学核心素养的自然发展.

3.2 引领深度思维是创新运用教材的归宿

引领深度思维是创新运用教材的最终归宿.对于不同的内容,编者为学生创造了不同的实践机会,教师若能创新运用教材,把握时机渗透数学思想方法,锻炼学生的深度思维,就能让学生的数学素养自然提升[3].在本课中,教师从学生已有认识出发创设的有效问题和设计的数学活动都是为了引领学生的深度思维,让学生在自主探究和合作交流中解决问题,发现结论,感受思想方法,感悟知识本质,发展创新能力,培养深度思维的习惯.

总之,教材是静态的,而教师的教学方法与学生的学习过程是动态的,挖掘教材内涵,创新使用教材,为学生创造生动、深入的课堂,引领学生深度思考,定会更好地促进学生数学素养的养成.