特征参数对微混喷嘴内燃料与空气混合均匀性影响
陈炫任,王 辉,王 超,张 旭,陈 冬,唐嘉诚
(哈尔滨工业大学 能源科学与工程学院,黑龙江 哈尔滨 150001)
0 引 言
煤炭在中国能源行业占主要地位,然而当今温室效应等环境问题日益严重,低碳化已是大势所趋,因此煤炭的洁净化利用将是未来煤炭产业可持续发展的关键。整体煤气化联合循环(Integrated Gasification Combined Cycle, IGCC)发电被认为是目前最具发展前景的技术手段之一[1-3]。由于制备方法不同,合成气的组分多变,可燃组分包括H2和CO,其中,氢气具有较高的火焰峰值温度及火焰传播速度,若直接将合成气利用于传统燃气轮机中,将面临严重的NOx排放超标和回火等问题[4-6]。微混合燃烧技术(Micro-mixing Combustion, MMC)是针对氢及含氢合成气提出的一种极具前景的燃气轮机燃烧技术[7]。该燃烧室采用大量毫米级直管喷嘴(喷嘴出口直径为10 mm级别)代替传统燃烧室内大尺寸旋流喷嘴,其目的是缩小燃料与空气的混合尺度,因此称为微混,通过该方式可降低NOx排放;此外,直管喷嘴可去除喷嘴出口处回流区,提升出口燃气流速降低富氢燃料的回火风险[8-9]。目前,GE、三菱、NASA等公司以及各研究机构[10-13]已对微混燃烧技术开展了大量研究,结果表明[14-17],微混燃烧器在实验室规模下表现出良好的排放性能,可将NOx排放浓度降至10×10-6以下,可见将该技术作为重型氢气燃气轮机的未来发展方向具有可行性。
由于微混喷嘴尺寸为毫米级别,无法简单通过增加预混距离来改善燃料和空气的混合均匀性,因此提升微小尺度下燃料与空气的混合质量[18]是改善微混喷嘴性能以及降低微混燃烧器污染物排放的关键。ARAOYE等[19]研究微混喷嘴非反应流动特性及混合特性,发现混合质量主要取决于主流与射流的动量比,且当混合距离大于10d(d为微混喷嘴直径)时质量扩散为混合的主导因素,动量扩散影响较小。LIU等[20]通过3种RANS模型对微混模型燃烧器的混合特性进行预测,发现Standardk-ε在沿程上的计算结果普遍高于Realizablek-ε和SSTk-ω两种模型,且随预混距离的增加差别逐渐减小。CHEN等[21]研究了结构参数改变对微混喷嘴混合特性的影响,发现缩短预混通道射流方向的直径可有效提升混合均匀性,但改变燃料孔直径对混合质量的影响不明显。
现阶段有关微混燃烧技术混合特性的研究较少,且相关文献主要探究结构参数变化对混合质量的影响规律,为定性分析,无法形成关键结构参数与混合特性的半经验公式。此外,由于微混合喷嘴结构与传统大尺寸旋流喷嘴存在较大区别,因此不能直接采用传统燃气轮机燃烧室的相关公式进行计算。笔者提取单只微混喷嘴的特征参数,计算不同特征参数下喷嘴内混合均匀性,并通过计算结果形成关于特征参数与混合均匀性的半经验公式,为微混喷嘴设计提供参考。由于微混喷嘴尺寸为毫米级别,内部的物质场很难通过试验测试,因此本研究通过数值模拟完成,并通过喷嘴出口位置的混合均匀性试验结果来验证数值模拟的准确性。
1 数值模拟方法
1.1 几何模型介绍
1.1.1 模型描述


图1 单只微混喷嘴结构示意
1.1.2 特征参数选取
根据相关文献[22],微混喷嘴内燃料与空气掺混过程的主要影响因素为:雷诺数Re、射流动量比mj、相对预混长度z/d、燃料平均流速v。雷诺数Re表示流动过程的湍流度;射流动量比mj表示空气和燃料在掺混初始阶段的流动特性;燃料入口平均流速v表示预混气在预混通道内的停留时间;相对预混长度z/d表示预混空间尺寸。
微混喷嘴内雷诺数Re计算公式为
(1)
式中,ρair为空气入口密度,kg/m3;vair为空气入口速度,m/s;μ为空气黏度系数,kg/(m·s)。
相对预混长度z/d计算公式为
(2)
射流动量比mj计算公式为
(3)
式中,ρfuel为燃料入口密度,kg/m3;vfuel为燃料入口速度,m/s。
燃料入口平均流速v计算公式为
(4)
1.2 模型及边界条件选取
根据计算微混喷嘴内最大马赫数小于0.3,因此模拟是基于不可压缩理想气体假设进行。燃料组分为体积比1∶1的H2与CO合成气,入口速度为35 m/s,入口温度15 ℃;空气入口速度为50 m/s,入口温度为418 ℃;出口设置为压力出口。此外,根据前期研究结果[21],Large-eddy simulation(大涡模拟,LES)模型对微混燃烧器冷态计算的预测结果较为准确,故选择商业软件fluent中的LES作为湍流模型,所采用的数值模拟设置见表1。数值模拟的能量收敛标准为残差值低于1×10-6,其余全部残差小于1×10-3时的迭代结果作为收敛结果。

表1 本文采用的数值模拟设置
1.3 网格划分及无关性验证
由于微混喷嘴几何结构较为复杂,因此采用多面体网格与六面体网格对其进行划分,使其相比四面体网格在保证相同精度的前提下降低计算成本,同时保证较小的网格扭曲度。计算域的网格划分结果如图2所示。此外,在划分网格时对燃料孔位置及喷嘴出口位置进行了局部加密。根据不同的局部尺寸划分了103 500、135 100和172 700的3组不同数量的网格。对比喷嘴出口处的轴向速度分布(图3),发现135 100和172 700方案的结果基本重合。因此,选择由135 100方案网格作为计算网格。135 100方案网格内部最小网格尺寸为0.05 mm,最大网格尺寸为0.8 mm,平均网格质量为0.89,无量纲壁面距离(y+)近似1。

图2 微混喷嘴内部网格结构

图3 网格无关性验证结果
2 数值模拟准确性验证
模拟前,需对所采用的运行参数和数值设置进行可行性和准确性验证。试验与数值模拟在相同喷嘴结构相同工况下展开。通过背景纹影方法对喷嘴出口位置的混合匀度性进行测试。试验装置示意如图4所示。其中,空气入口温度由电加热炉控制。对于测量系统,采用激光照亮背景,在激光和背景之间设置透镜,产生平行于光轴的光束。平行光束穿过背景和测量区域,背景为印有随机分布点的光学玻璃。

图4 背景纹影测试装置
对于混合特性试验,采用等体积流量的CO2代替燃料进行测量。首先拍摄不含CO2的参考图像,记录光束无偏转通过的原始背景图案。然后由中心管注入CO2,在预混通道内与空气混合。当光束通过预混气体时,由于气体(CO2和空气混合气)与空气折射率的差异,光发生偏转,这一现象被摄像机捕获。图像处理方法可由文献[23]获得。
对比60~420 ℃(以60 ℃为间隔)空气入口温度范围内的喷嘴出口处混合均匀度,混合均匀度γa计算公式[24]为
(5)
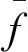
不同空气入口温度下通过试验测试以及数值模拟计算的混合均匀度结果如图5所示。由于混合均匀度在0.9以上,因此出口气流波动会对混合质量产生很大影响。因此模拟结果与试验结果存在一定偏差。总体来看,试验结果与数值模拟结果的偏差在5%以内,说明数值模拟结果基本可信。
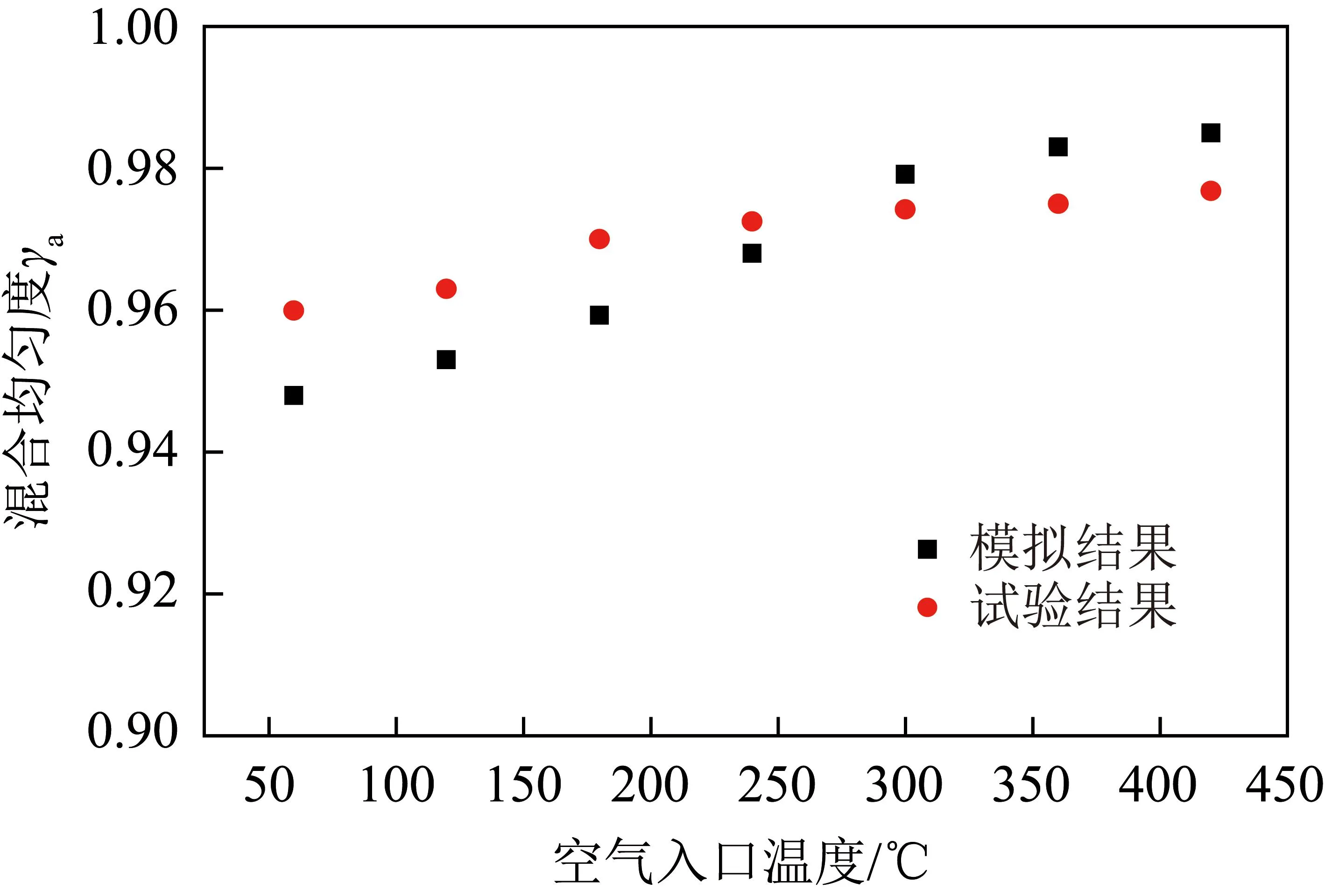
图5 试验结果与数值模拟结果对比
3 结果与讨论
3.1 微混喷嘴内燃料与空气的混合机理
为明确微混喷嘴内燃料与空气的混合机制,通过Ω方法[25]提取微混合管内的三维涡(等值面Ω=0.52)并结合燃料浓度分布分析燃料与空气的混合过程,结果如图6所示。三维涡的位置为燃料与空气的主混合区域。燃料流从燃料孔口喷出,并在横流空气作用下形成反向涡对(Counter-Rotating Vortex Pair,CVP),燃料与空气在微混喷内受CVP涡的裹入作用进行混合。且涡量CVP涡的裹入能力越强,燃料与空气掺混的速度越快。
图6 燃料与空气掺混过程中的三维涡结构
3.2 燃料入口平均流速对混合特性的影响
图7为在射流动量比mj=0.032、雷诺数Re=1.33×105条件下,相对预混长度z/d及燃料入口平均流速v对混合均匀度γa的影响规律。由图7可知,随预混距离增加,燃料与空气具有更大的掺混空气,混合均匀度明显提升。然而燃料速度增大对混合特性的影响不明显;且在流速较低时混合质量有小幅提升,这是由于当燃料平均流速较低时,燃料与空气在预混通道内停留时间更长。

图7 不同预混距离下的混合均匀度
不同射流动量比下的混合质量如图8所示。在Re=1.33×105、预混距离z/d=3的条件下,提高燃料与空气动量比可有效提升混合均匀度。在较高的动量比下,燃料与空气掺混更剧烈,因此在相同掺混距离下混合均匀度更高。此外,由图8还可知,射流动量比变化时,燃料入口流速对混合均匀度γa的影响可以忽略。

图8 不同射流动量比下的混合均匀度
图9为不同雷诺数下的混合特性计算结果,可知相对预混长度z/d=3、射流动量比mj=0.032、喷嘴内部雷诺数增加时,γa总体呈下降趋势。且与燃料入口速度相比,雷诺数对混合特性的影响更显著。

图9 不同雷诺数下的混合均匀度
对比上述特征参数对混合均匀度的影响规律可知(图7~9),燃料入口平均流速变化时预混通道内混合均匀度的变化在0.03以内,这是由于预混通道环管间距仅1.05 mm,燃料入口速度的变化不会显著影响燃料的射流深度,因此可忽略燃料入口平均流速v对混合特性的影响。
3.3 雷诺数比对混合特性的影响
为探究雷诺数对混合质量的影响,选取Re=1×105~2×105下的混合均匀度,不同雷诺数下的混合均匀度在预混距离下的分布如图10所示。为保持其余特征参数不变,通过等比例放大或缩小喷嘴结构改变雷诺数。由图10可知,混合特性随燃料与空气动量比的增加明显提升,与前文结论一致;此外,对比各雷诺数下的混合质量可知,在预混距离和动量比相同时,各方案的混合均匀度在Re≥1×105时基本不变,这是由于在雷诺数较高时,喷嘴内部流动到达了第二自模化区,即无需保持相同雷诺数即可满足流场相似原理,此时可忽略雷诺数对混合特性的影响。此外,当射流动量比为0.047,在预混距离z/d=5位置处混合均匀度可达90%以上,表明燃料与空气在喷嘴出口附近已实现均匀混合。

图10 不同雷诺数下的混合均匀度在预混距离下的分布
综合第3.2与第3.3节结论可知:在进行特征参数对混合均匀度进行拟合时,可以忽略相对燃料入口速度及Re≥1×105时雷诺数的影响。由此,进一步分析拟合相对射流动量比mj及相对预混长度z/d对混合均匀度γa的影响。
图11为不同射流动量比下各位置处的混合均匀度。从曲线整体变化趋势来看,当相对预混距离z/d≥4时,射流动量比增加对混合均匀度的影响降低。这是由于燃料与空气的掺混主要受动量扩散与质量扩散主导[19]。在燃料与空气掺混前半段,动量扩散为混合的主导;但随混合的进行燃料流与空气流动量差别减小,最后汇聚成一股流体,因此在混合后半段,质量扩散成为混合的主导因素,动量对混合特性的影响逐渐消失。

图11 不同设流动量比下各位置的混合均匀度
3.4 特征参数对混合特性的拟合
根据预混距离与射流动量比对混合特性的影响规律,可对混合均匀度进行拟合,射流动量比和预混长度对混合均匀度拟合结果如图12所示。
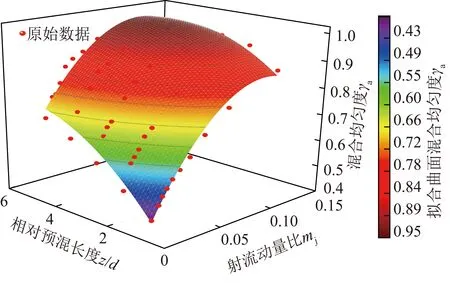
图12 射流动量比和预混长度对混合均匀度拟合结果
通过PLOY2D函数对射流动量比mj、相对预混长度z/d和混合均匀度γa进行拟合,并采用Leverberg-Marquardt算法对拟合结果进行优化,所得到的拟合公式为
(6)
回归系数R2可达0.98,对比原始数据与拟合曲面,可以发现拟合效果较优。
3.5 不同运行工况下混合均匀度拟合公式的准确性检验
在第3.2~3.4节中,特征参数变化时不涉及运行工况的改变,但是在燃气轮机实际工作中,需满足在入口工况发生变化时仍能保证稳定工作,因此需对第3.4小节所得拟合公式进一步检验,使其在一定工况范围内仍能准确预测混合均匀度。由于研究主要为冷态内容,燃料组分不会对混合特性产生显著影响,因此本文主要研究入口工况包括当量比以及入口空气温度。
3.5.1 不同当量比下的混合均匀度拟合结果
为检验当量比变化时混合均匀度拟合公式的准确性,对当量比0.5~1.0的混合特性进行模拟,并与拟合结果进行了对比,结果如图13所示。考虑到中低热值合成气在较低当量比条件下可能会出现不稳定燃烧,因此未考虑当量比低于0.5方案。当量比增加的同时射流动量比相应增加。可知当量比变化时,混合均匀度拟合公式在所对应的射流动量比范围内保持了较好的预测结果。
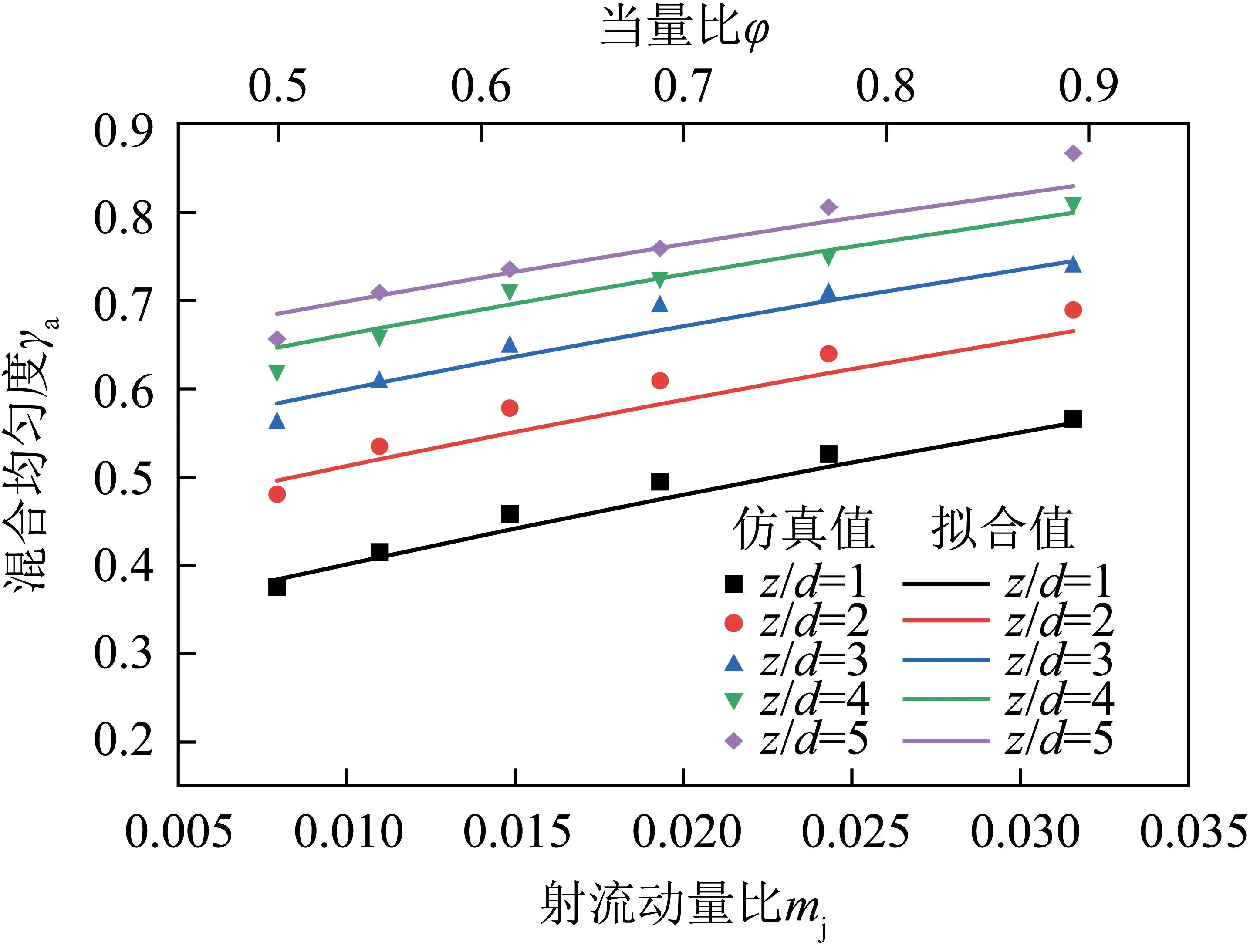
图13 不同当量比下的模拟结果与拟合结果
3.5.2 不同入口空气温度下的混合均匀度拟合结果
空气入口温度对燃烧室燃烧特性有显著影响,因此有必要探究拟合公式在不同温度下的适用性。图14为入口空气在18~818 ℃时的拟合结果与模拟结果对比(由于微混喷嘴尺寸较小,无法通过试验获得混合均匀性,因此通过数值模拟结果检验拟合结果的准确性)。空气温度的变化影响空气密度进而影响射流动量比。由对比结果可知,当相对预混距离z/d≤4时,拟合曲线与模拟结果基本重合;在z/d>4时,二者差别略增加,最大误差为4.35%。因此总体来看,拟合结果的准确性较高。
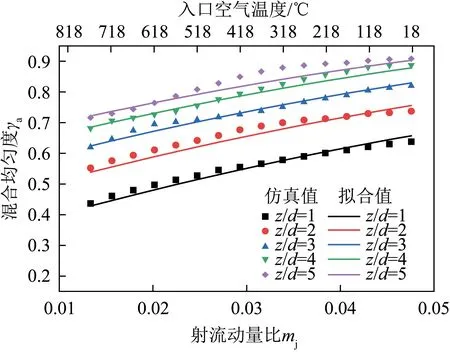
图14 不同入口空气温度下的模拟结果与拟合结果
因此,所得到的拟合公式在当量比在0.5~1.0、雷诺数Re≥1×105、空气入口温度18~818 ℃的条件下适用,可对微混喷嘴的混合质量进行准确预测,误差普遍在5%以下。且根据公式所涉及的相对射流动量比及相对预混通道长度对喷嘴结构中的预混通道直径以及预混通道长度进行相应优化,为单只微混喷嘴设计提供经验。
4 结 论
1)在燃料与空气混合过程中,微混喷嘴内会形成反向涡对,燃料在该涡的裹入作用下与空气混合。
2)预混通道距离及射流动量比变化对微混管内的混合均匀度有显著影响,且随预混距离增加,对混合特性的影响降低。
3)由于微混喷嘴的预混通道等效直径在毫米级,燃料入口平均速度对混合均匀度的影响较小;此外,当雷诺数大于1×105时,喷嘴内流动进入第二自模化区,混合特性不再受雷诺数影响。
4)通过射流动量比及预混通道距离对微混喷嘴的混合均匀度进行拟合,回归系数R2可达0.98,且当量比为0.5~0.8、空气入口温度18~818 ℃时拟合结果误差能保持在5%以下,可知所得拟合公式对于混合均匀度预测的准确性较高。因此,将该公式可作为设计准则,为微混喷嘴在混合特性提供结构优化方案。

