基于过渡电阻倾斜角的风电T接双电源系统自适应距离保护方案
传云,王维庆,王海云,武家辉
(新疆大学 可再生能源发电与并网控制教育部工程研究中心,乌鲁木齐 830047)
0 引 言
随着传统能源的日益衰竭及风电技术的不断完善,风电大规模接入配电网导致电网表现出许多异于常规电网的故障特征[1-5],给常规保护装置的选择性、灵敏性及可靠性带来了很大的挑战[6-10]。风电以T接方式并网的系统保护因其特殊性也得到国内外学者的广泛关注。目前,有许多学者对此问题展开了大量研究[11-14]。文献[11]针对T接线路提出余弦相似度特征判据用以解决传统差动保护存在的区外故障可靠性与区内故障灵敏性不兼容的问题。文献[12]指出常用差动保护判据在T接线路上存在的局限性并提出综合保护判据,提高保护的灵敏性及可靠性。文献[13]指出新能源电源相角畸变、幅值受限对比率式电流差动保护带来很大影响,在并入强同步系统时容易造成灵敏度下降,并入弱同步系统时存在拒动风险。文献[14]根据线路母线电压互感器的信息,以线路两端正序补偿电压之间的差值作为辅助判据消除逆变型DG接入对电流纵差带来的影响。文献[15]提出一种适用于多节点T接线路的差动保护方案,对多点T接线路出现的电流汲取与T点增加带来的灵敏度问题提供了一种很好的解决方案。
上述针对T接线路保护的研究中主要运用差动保护这种方法,但差动保护对通信要求较高。距离保护具有保护区稳定并且受系统运行方式变化影响小的特点,在高压配电网中应用较多。文献[16-17]对传统距离保护进行适应性分析,指出测量阻抗表达式中包含附加阻抗会引起传统距离保护误动与拒动,进而提出用纵联保护来解决T接区域内故障的方案,但改变继电保护方案投资巨大,经济性与现实可行性较差。文献[18]分析了风电T接对本段保护及下段保护造成的影响,仿真验证了故障位置、风机出力及过渡电阻等对距离保护造成的具体影响,但没有提出如何消除附加阻抗的具体解决方案。
针对现有文献对于风电T接线路在距离保护方案上研究的欠缺,文章提出一种适用于风电T接系统的自适应距离保护方案。文中首先分析了风电T接对电网传统距离保护产生的影响,得出当过渡电阻与电源短路电流故障分量共同作用下,产生的附加阻抗使保护整定过程变得较为复杂,可能会使传统保护发生误动或拒动。为了解决上述问题,文中从测量装置处获取各电源出口母线处的故障电流分量用于计算过渡电阻倾斜角,在过渡电阻未知的情况下,利用各阻抗与R轴之间的夹角关系对测量阻抗进行修正使其能跟踪到短路阻抗。最后通过MATLAB/Simulink仿真验证所提方案的有效性与正确性。
1 风电T接对传统电网距离保护的影响
图1为风电T型接入含双电源的常规配电网的母线中,其中EM与EN为常规电源等效电动势,EW为风电等效电动势,通过升压后并入B母线,F1与F2为故障点。考虑到风电的联络线相对较短,即故障概率远小于其他线路,所以本文暂不分析风电联络线发生的故障,主要分析风电接入系统母线后,在风电T接点上下游线路发生单相接地故障对距离保护装置产生的影响。

图1 风电T接系统示意图
1.1 风电T接对上游保护产生的影响
当故障位置在F1处时,取T接线路为研究对象,将以外区域等效为电源和阻抗串联的形式,如图2所示。
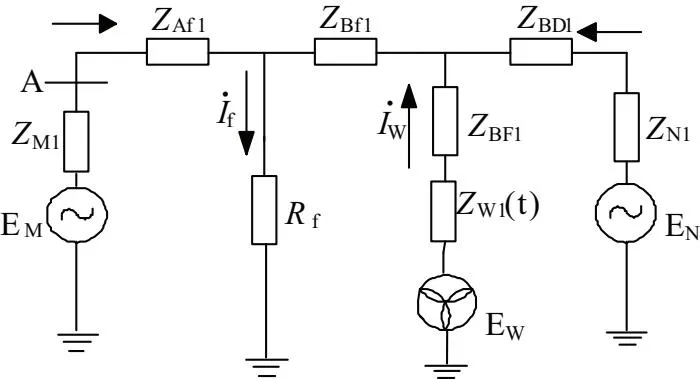
图2 F1处发生故障时的等效电路图
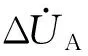
(1)

测量阻抗ZMA为:
(2)


图3 附加阻抗对保护装置的影响
1.2 风电T接对下游保护产生的影响
当故障发生在F2处时,系统的故障等效电路图如图4所示。
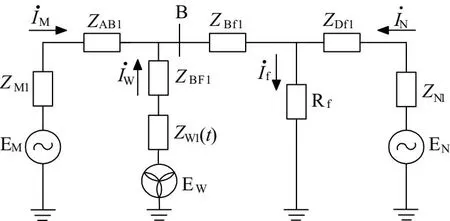
图4 F2处发生故障时的等效电路图
(3)

测量阻抗ZMB为:
(4)
式(4)中,ΔZ表示附加阻抗。由式(4)可以看出,测量阻抗在金属性故障时ΔZ为零,短路后对传统保护装置动作特性没有影响。当在非金属性故障时,ΔZ的值受到ΔIM、IM0、ΔIN、ΔIW、IW0及Rf这几个因素的影响。相比于其他几个故障电流分量,ΔZ受Rf影响较大。ΔZ呈感性时会使母线B的测量阻抗变大,严重时将引起保护装置拒动。ΔZ呈容性时会使母线B处测量阻抗变小,严重时将引起保护装置误动。
2 基于过渡电阻倾斜角的自适应距离保护方案
由上节分析可知,当线路T接点上游发生故障时,ΔZ受到ΔIM、IM0、ΔIN、ΔIW及Rf因素的共同影响,具体表现为ΔZ随着ΔIN、ΔIW及Rf的增大而增大,ΔZ随着ΔIM与IM0的增大而减小,从而导致保护装置的不正确动作,因此考虑在测量阻抗的基础上,消除附加阻抗ΔZ,从而保证各保护装置的正确动作。ΔIM、IM0、ΔIN、ΔIW这几个电流故障分量可以通过在保护安装处获得。对于Rf,却不容易测得,因此本文考虑利用向量图对测量阻抗进行修正,在Rf未知的情况下,利用各阻抗与R轴之间的夹角关系对测量阻抗进行修正,使修正后的阻抗能跟踪到短路阻抗。同理,当线路T接点下游发生故障时按照上述思路对测量阻抗进行修正。
2.1 利用向量图修正测量阻抗
当T接点上游发生单相接地故障时,由式(2)中附加阻抗ΔZ,定义过渡电阻倾斜角[21]为:
(5)
同理,当T接点下游发生单相接地故障时
(6)
可以采用向量图的方法,对测量阻抗轨迹进行修正,具体步骤如下:
1)获取测量阻抗ZMA在向量图中画出ZMA,其中ZMA与R轴夹角为γ。
2)通过测量阻抗ZMA画水平线,由(5)式计算得到的过渡电阻倾斜角θ1,然后画出与该水平线成夹角θ1的射线,定义为附加阻抗ΔZ1。
3)已知线路阻抗角β,通过原点画出与R轴成β角的射线,于ΔZ1相交于d1点,则Zd1表示修正后测量阻抗。
向量图如图5所示,图中ZSET表示整定圆直径,当θ1>0,则ΔZ1是向上倾斜指向Zd1。同理,若θ2<0,则ΔZ2是向下倾斜指向Zd2。
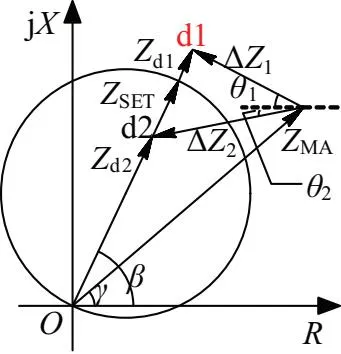
图5 修正测量阻抗的向量图
根据三角函数正弦定理,则Zd的理论计算如式(7)所得:
(7)
式(7)中θ为过渡电阻倾斜角,对于风电T接点上游的阻抗继电器可以由式(5)求得,T接点下游的阻抗继电器可以由式(6)求得,而式(5)和式(6)中的所有参数可以通过在保护安装处测量得到。γ为测量阻抗ZMA与R轴夹角,β为线路阻抗角,均为已知,所以可以计算得到修正后的测量阻抗。由图5及式(5)或(6)中可见,当过渡电阻一定且未知的情况下,通过计算过渡电阻倾斜角,可以判断出修正后的线路测量阻抗Zd是否落入阻抗整定圆内,从而判别线路是否发生故障,进而决定保护装置是否动作。
综上所述,由式(5)和(6)可知,随着线路上故障位置、系统运行状态、过渡电阻值的变化,包含这几个因素的过渡电阻倾斜角能够自适应的跟着上述几个因素的变化而变化,然后根据式(7)中计算结果反映出短路真实位置,有效提高保护装置动作可靠性。
2.2 保护方案流程图
保护方案流程图如图6所示。

图6 保护方案流程图
根据上节中对测量阻抗的修正方法制定保护方案如下:
1)数据滤波及故障选相。当故障发生后,使用傅里叶算法对采样数据进行滤波处理,再利用选相元件判别出故障类型及故障相。
2)计算过渡电阻倾斜角。从各电源母线处获取电流故障分量。对于风电T接点上游的阻抗继电器按照式(5)计算过渡电阻倾斜角,T接点下游的阻抗继电器按照式(6)计算过渡电阻倾斜角。
3)对测量阻抗进行修正。通过计算过渡电阻倾斜角θ、测量阻抗ZMA、线路阻抗与R轴的夹角β、测量阻抗与R轴的夹角γ这几个数据,将其代入式(7)中计算修正后的测量阻抗Zd。
4)保护判定。若修正测量阻抗在本段保护动作区域内,则保护装置动作。若在区外,则保护装置不动作并返回至第一步。
3 算例仿真
3.1 系统建模
参照风电场接入电网标准[22],利用MATLAB/Simulink仿真平台上搭建如图1所示的风电T接系统仿真模型。系统电压等级为110 kV,M侧和N侧电源的正序阻抗参数均为ZSM1=0.69+j7.97 Ω,零序阻抗为ZSM0=1.03+j11.9 Ω,W侧的风电额定容量为18 MW,负荷均为15 MW。线路AB、BC、CD长度均为100 km,线路BF长度为10 km,线路参数为正序阻抗为ZL1=0.0363+j1.006 Ω/km,零序阻抗ZL0=0.3976+j1.328 Ω/km。
3.2 仿真验证
为验证所提自适应距离保护方案的正确性,本文在风电T接点上、下游单相接地短路的情况分别进行仿真,并通过改变故障位置、过渡电阻、系统电源相位、风电运行方式验证所提方案的自适应性。初始条件按如下设定:双馈风机的风速为15 m/s,输出功率为9 MW,模型采样时间为5 μs,故障持续时间0.1 s,过渡电阻取20 Ω,故障位置在本段线路50%处,M侧和N侧电源的相位差为30°,整定距离取本段线路的85%。
阻抗修正按照前面2.1节修正测量阻抗的方法,把测量阻抗轨迹上每一个点均映射到线路阻抗角的直线上,形成看起来像一条线段的所有点的集合。
3.2.1 保护方案对T接点上游故障的适应性分析
保持上述初始条件不变,故障位置分别取本段线路的25%、50%、75%,验证所提方案对上游故障位置变化时的自适应性。仿真结果如图7所示。

图7 保护方案对上游故障位置变化的适应性分析
由图7可知:随着故障位置在本段线路上的变化,电抗对于阻抗测量轨迹影响比电阻大。当在线路75%处发生故障时,原保护装置出现拒动,而本文所提保护方案中阻抗修正轨迹能跟踪到短路点阻抗,能克服原保护的拒动风险。
3.2.2 保护方案对过渡电阻的适应性分析
保持上述初始条件不变,过渡电阻分别取0.1 Ω、10 Ω、30 Ω、50 Ω,验证所提方案对过渡电阻变化的自适应性。仿真结果如图8所示。

图8 保护方案对过渡电阻变化的适应性分析
由图8可知:过渡电阻越小,测量阻抗曲线变化越剧烈,说明在短路稳定阶段测量阻抗上下波动幅度也越大。当过渡电阻为30 Ω时,测量阻抗进入保护整定边缘。当过渡电阻为50 Ω时,测量阻抗轨迹已远离整定圆。而本文所提保护方案在各种不同过渡电阻的情况下,均能跟踪到线路短路点阻抗,使保护装置正确动作。
3.2.3 保护方案对系统电源相位的适应性分析
保持上述初始条件不变,系统电源EM与EN的相位差分别为30°、45°、60°,验证所提方案对电源相位变化时的自适应性。仿真结果如图9所示。

图9 保护方案对系统电源相位变化的适应性分析
由图9可知:系统电源相位差越大,测量阻抗轨迹向上有轻微偏移量。相对于故障位置、过渡电阻而言,系统电源相位差对测量阻抗影响很小。
3.2.4 保护方案对风电运行方式的适应性分析
保持上述初始条件不变,风电分别按下面三种运行方式,如表1所示,验证所提方案对风电运行方式变化的自适应性。仿真结果见图10。
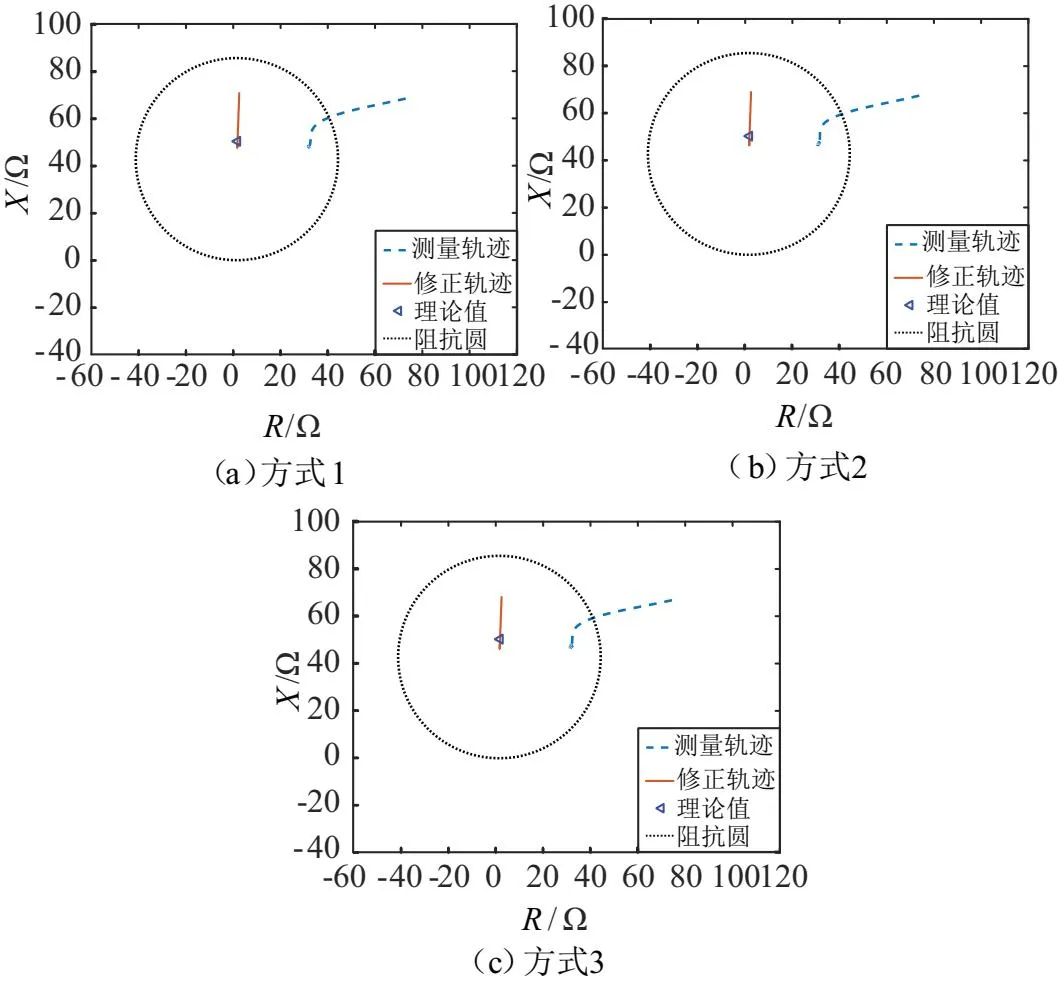
图10 保护方案对风电电源变化的适应性分析
由图10可知:阻抗测量轨迹在上述三种方式下几乎不变,这是因为风电电源提供的短路电流幅值受限,会远远小于系统电源的提供的短路电流,所以对测量轨迹基本没有影响。
3.2.5 保护方案对T接点下游故障的适应性分析
保持上述初始条件不变,故障位置分别取T接点下游线路的25%、50%、75%处,验证所提方案对下游故障位置变化时的自适应性。仿真结果如图11所示。
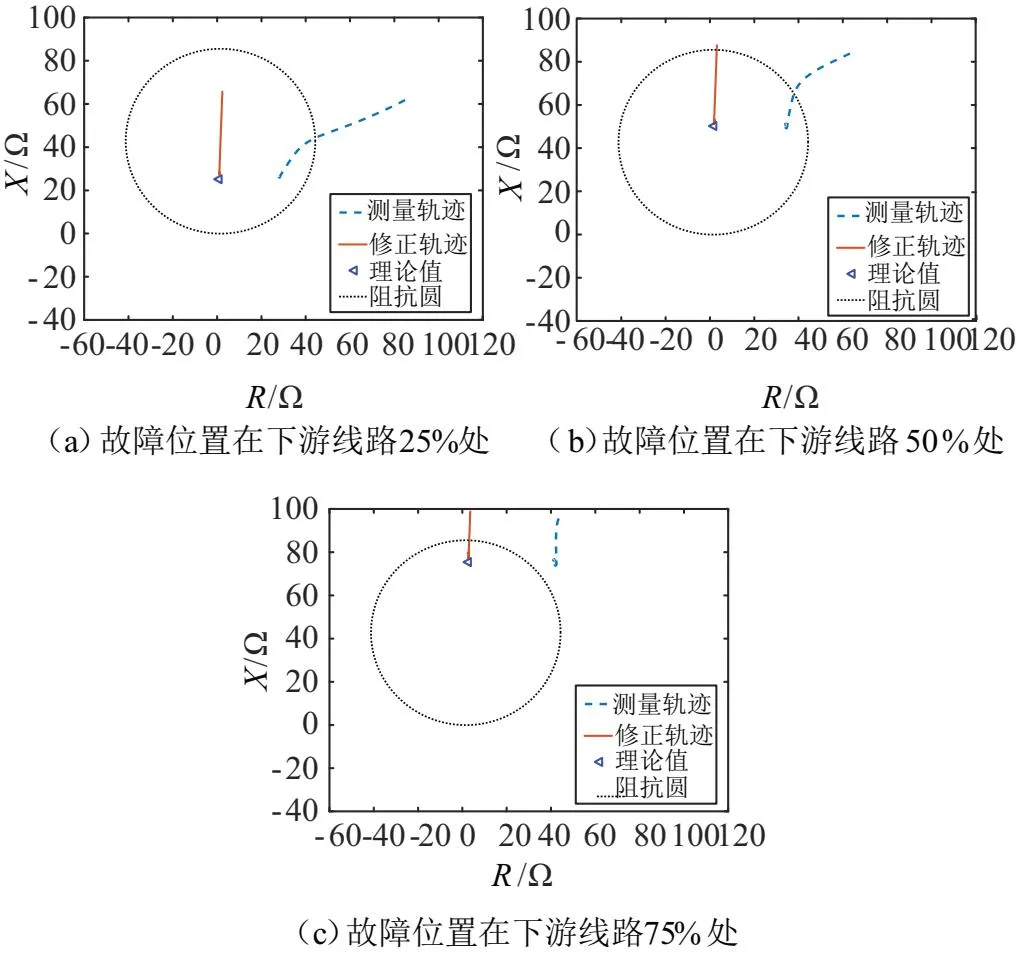
图11 保护方案对下游故障位置变化的适应性分析
由图11可知:当下游线路故障时,从阻抗测量轨迹可以看出,受谐波影响比上游线路故障时更大。当在线路75%处发生故障时,原保护的阻抗测量轨迹偏离阻抗整定圆,发生保护装置拒动。而文章所提保护方案能跟踪到短路点阻抗,保证保护装置的正确动作。
4 结束语
针对风电T接对传统距离保护的影响,文章提出基于过渡电阻倾斜角的风电T接双电源系统自适应距离保护方案,主要结论如下:
1)在风电T接双电源系统后,阻抗继电器所测得的阻抗除了线路本身短路阻抗外还包含附加阻抗ΔZ。当ΔZ呈感性(容性)时,会使测量阻抗变大(变小),严重时将引起继电保护装置拒动(误动)。
2)通过分析附加阻抗ΔZ的构成,考虑到过渡电阻不易测量,文中利用各阻抗与R轴之间的夹角关系消除掉过渡电阻对保护装置产生的影响,能自适应修正测量阻抗使其能跟踪到短路阻抗。
3)仿真结果表明文中所提方案受故障点位置、过渡电阻、电源相位差及风电运行方式影响较小,可以使保护装置可靠动作。该方案简单有效,无需改造原距离保护装置,经济性与现实可操作性较高,具有一定现场工程指导意义。
限于篇幅,本文只分析了单相接地故障,上述分析方法同样适用于其他接地故障。

