不同含水量砂岩的中红外光谱特征与预测模型研究

陈 露，常龙飞，沈沐傲，张鸣原，李德建*，李英骏，3*

（1.华北科技学院 应急技术与管理学院，河北 三河 065201；2.中国矿业大学（北京） 深部岩土力学与地下工程国家重点实验室，北京 100083；3.中国科学院物理研究所，北京 100190）

水对岩石具有明显的弱化、渗透、水楔和溶蚀作用［1］，岩石表面的水分子可通过吸引力与具有较弱连结强度的矿物分子相结合。水分子进入岩石颗粒间隙，将减弱岩石中矿物成分的粘聚力，使矿物颗粒间起连接作用的胶体矿物与水相互作用产生润滑效果，进而导致岩石强度降低。因此，明确岩石中的水分含量对于地下工程的安全开展至关重要。

红外光谱技术能无损快速地获取物质的光谱信息［2-5］，是动态监测物质含水量的有力手段。Savin等［6］分析了土壤表面光谱反射率与其水分含量的关系，发现土壤水分含量变化与光谱反射率的变化在短时间内同步。Huang 等［7］探究了受压阶段砂岩的光谱特征，发现砂岩的光谱特征变化与石英含量有关。张芳等［8］基于最大信息数研究了不同岩性对含水光谱特征的影响。中红外光谱分析技术 （MIR）具有更广泛的探测领域，表现出的光谱曲线能够凸显物质本身的属性，在定量分析方面也具有较大潜力，利用MIR分析岩石含水量与其光谱特征的关系仍有待探究。本文利用中红外光谱技术开展砂岩不同含水量的测试，通过宽波段范围的光谱特征观察砂岩对水的敏感响应波段并分析不同含水量砂岩的光谱特征，建立了基于中红外光谱特征的砂岩含水量反演模型，以期为岩石工程现场开采和勘探提供参考。

1 实验部分

1.1 样品制备

砂岩样品均采自甘孜藏族自治州泸定县，将其加工成高度100 mm，直径50 mm 的标准单轴岩石样品，选择质地较为均匀的6块样品（分别标记为A-1～A-6）进行光谱采集，样品如图1所示。

图1 砂岩样品示意图Fig.1 The diagram of sandstone samples

图2 不同含水量砂岩样品的中红外光谱采集过程Fig.2 The acquisition process of MIR spectra of sandstone samples with different water contents

为避免岩样内部的初始水含量不同，将样品平稳置于105 ℃的真空干燥箱内烘干3 d，利用精密电子天平测量其初始质量。将烘干后的砂岩样品分别平铺在100 ℃的恒温水浴锅中浸泡至样品中自由水基本消失且质量几乎不变，其质量分布如表1所示。

表1 砂岩样品质量分布Table 1 The quality distribution of the sandstone samples

1.2 方法与光谱采集

利用Foil 20-Z傅里叶变换中红外光谱系统进行光谱采集，采集范围为2.5～25 μm。在 23 ℃且湿度小于26%的恒温实验环境中，将样品放置在固定位置进行测定。探头的分辨率为4 cm，探头与测试样品之间的距离固定并与样品成90°夹角。每块岩样均经历从含水量为0到饱水状态，将其划分为11个含水量阶段。考虑到岩石的不均质性，每个岩样在相同含水量状态下分别从样品侧面和底部中心点采集光谱曲线2条。去除差异较大的光谱曲线数据，共获得不同含水量下较为稳定的光谱曲线230条。

砂岩样品在从干燥达到饱和状态的过程中，分别在样品底部（118 条）和侧面（112 条）采集不同含水量的光谱曲线。岩石是一种非均质多组分的晶体结构，其内部含有大量的孔隙和节理，表面平整度较差且相对粗糙，导致所得光谱整体反射率偏低，并且砂岩样品的光谱曲线在部分波段存在多而杂的“毛刺”。为更直观地获取光谱信息，利用FTIRDas系统对校正后的光谱数据进行SG（Savitzky-Golay）滤波平滑［9］。经筛选，确定窗口长度为5 的二阶SG 滤波平滑效果最佳。以相同含水量砂岩光谱样本的算术平均值作为样品光谱，不同含水量砂岩样品底部测试点处理后的光谱曲线如图3所示。

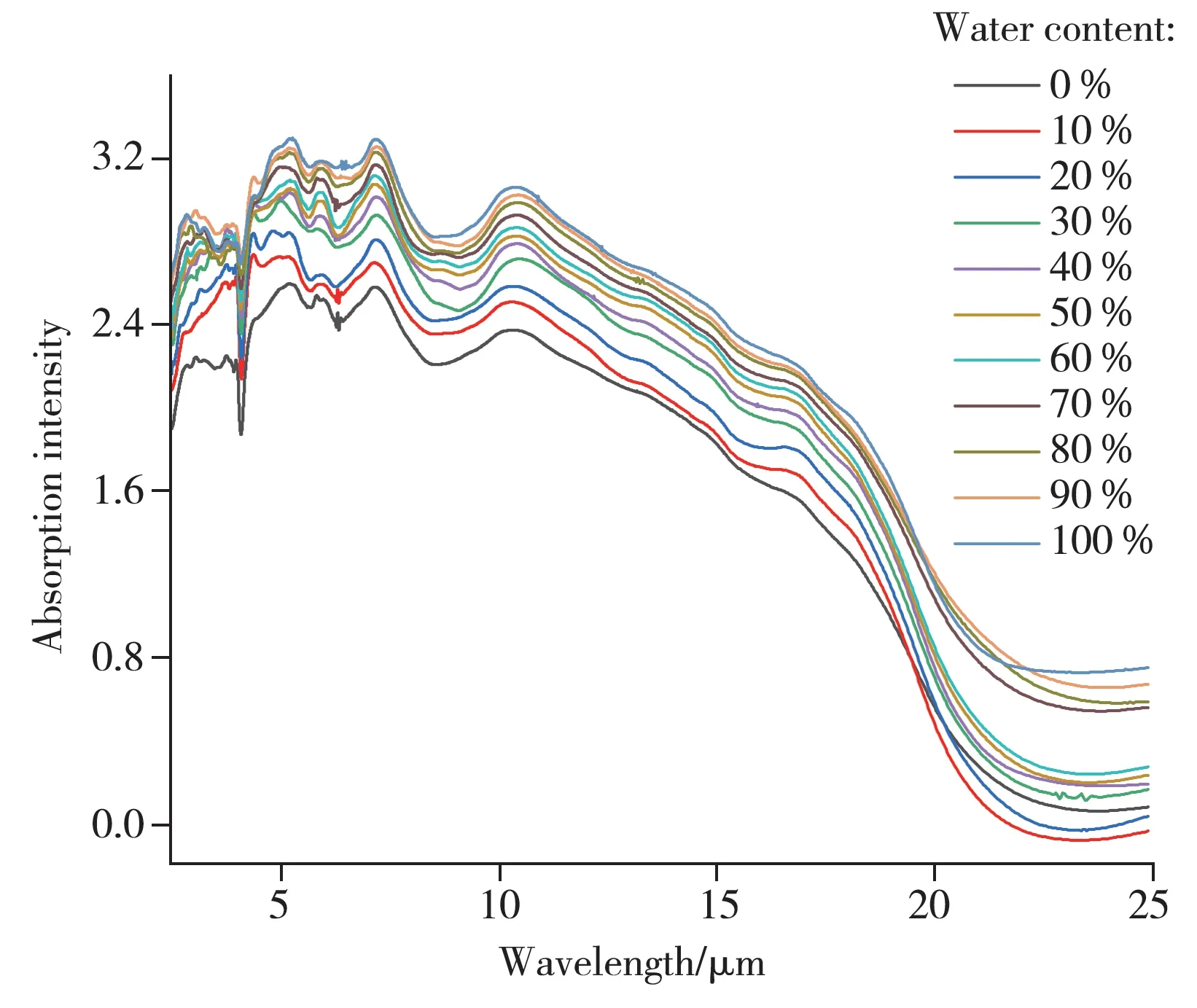
图3 不同含水量砂岩底部测试点的中红外光谱曲线Fig.3 The MIR spectral curves of test points at sandstone bottom with different water contents

2 结果与讨论

2.1 光谱差异分析

由图3 可知，不同含水量样品的光谱曲线分布基本一致，随着含水量的增加，光谱强度明显增加。图4 为不同含水量砂岩的二阶微分中红外光谱曲线，从图中可以看出在7.23 μm 和10.41 μm 附近存在明显的吸收峰（依次命名为峰R1和峰R2），且这两个吸收峰的波峰随含水量的增加而增强，峰顶位置逐渐向右偏移，说明砂岩样品分子在相应光谱波段范围内与水分子产生了相同频率的振动，导致能量跃迁。通常，水在近红外光谱中的吸收峰主要集中在O—H 伸缩振动的一级倍频1 440 nm及水分子的组合频1 940 nm 附近［10］，是其中红外吸收基频的倍频及合频。相较而言，中红外波段范围内的光谱曲线更能说明水分变量的特征，水在整个中红外光谱波段范围内的振动较为活跃，完全干燥与初始含水状态下的砂岩样品光谱差异最为明显，这是因为初始条件下水分覆盖在样品表面，样品表面与光波产生同频振动的分子数量明显增加，吸收的入射光增多，光谱曲线明显上升；随着水分的增多，水分子开始向岩石内部颗粒间隙扩散并逐渐趋于饱和。此时样品表面水分子含量变化不明显，不同含水量之间的光谱差异逐渐缩小，当波长超过11 μm时，不同含水量砂岩样品的中红外光谱的吸收能力逐渐下降。

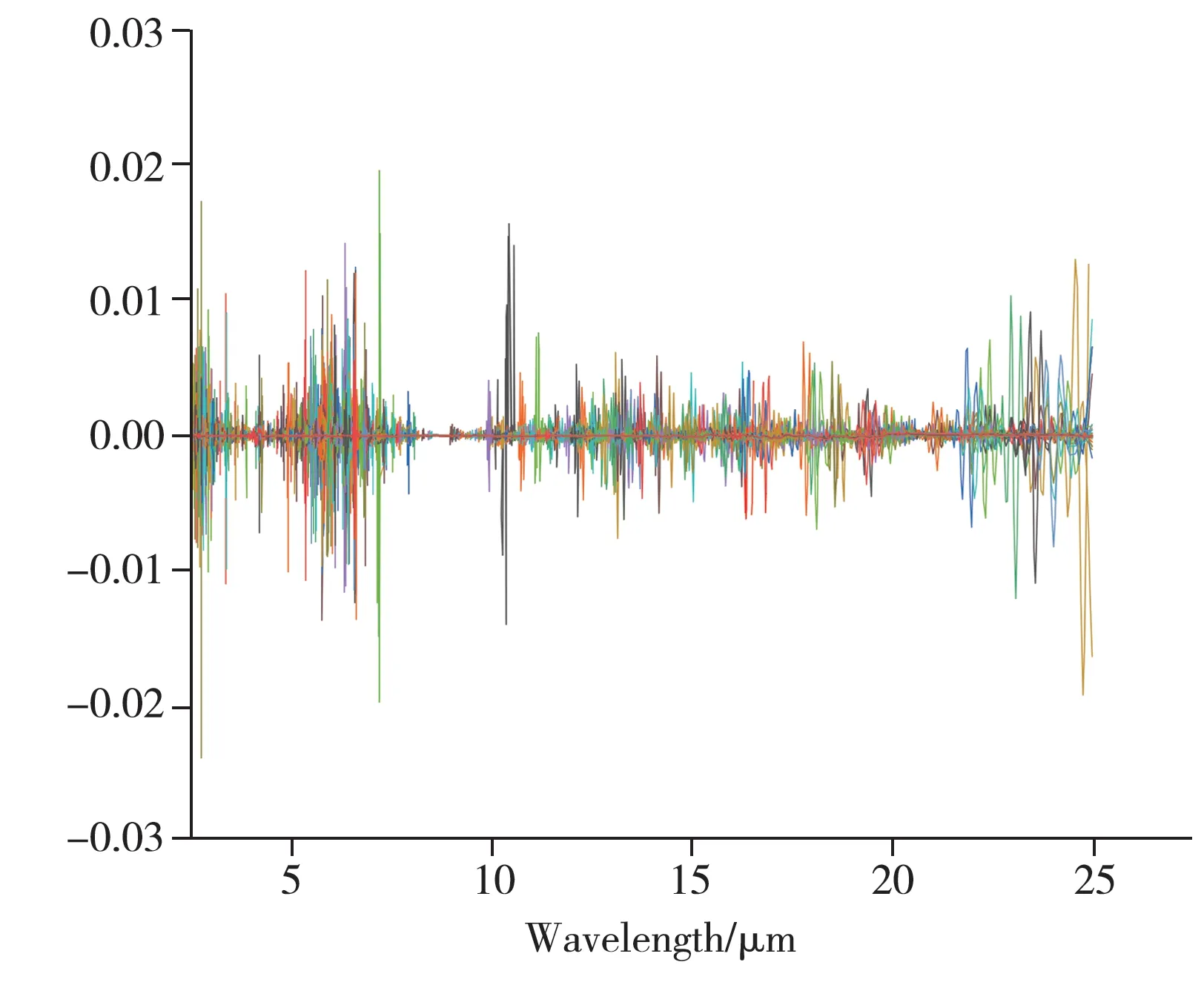
图4 不同含水量砂岩的中红外光谱二阶微分曲线Fig.4 The second order differential curves of MIR spectral of sandstone with different water contents

2.2 基于不同含水量砂岩光谱的预测模型构建

为消除散射、样本不均匀等误差影响，提高被分析信号中重要信息的权重，采用多元散射校正、归一化、一阶微分方法对光谱数据进行预处理。

2.2.1 结合多元散射校正与偏最小二乘法（PLS）的预测模型多元散射校正（MSC）［11］是将所有光谱数据取平均值作为“理想光谱”，并将其余光谱与平均光谱数据进行一元线性回归从而校正光谱。计算公式为：

式（1）中，n为样本数量，xi，j为由样本数和波长点数构建的光谱矩阵，为所有样本经简单处理后在相应波点处的平均值。式（2）中，xi表示单一样本的光谱数据，ki和bi分别代表光谱和平均光谱的相对偏移系数和平移系数。利用Matlab 对简单处理后的光谱数据进行多元散射校正，能够有效消除原始光谱数据由于噪声造成的基线平移问题。

将处理后的光谱曲线以3∶1的比例划分为训练集和测试集进行主成分分析［12］，通过比较主成分分析中前15个特征值的贡献率，发现前5个主成分的累计贡献率超过90%。根据这5个主成分得分计算各样本到训练集中心的马氏距离［13］，筛选异常样品并剔除离群点，在此基础上结合PLS［14］建立砂岩样本含水量的预测模型。马氏距离的计算公式为：

式中，Si为各训练集样本主成分的得分向量，Sˉ为总训练集样本的平均得分矩阵，M为训练集主成分得分的协方差矩阵，Di为各训练集样本的马氏距离，m为训练集的样本个数。

训练集异常样本阈值（Dth）的计算公式为：

式中，Dm为训练集样本马氏距离的平均值，σd为相应的标准差，e为权重系数。

通过计算得到预处理后训练集光谱样本的马氏距离如图5 所示。若数据的标准差较大，说明数据分布较为分散，可以适当放宽阈值，避免漏检异常样本；若数据的标准差较小，则说明数据分布比较集中，可适当缩小阈值，以减少误检正常样本。使用最优阈值调整权重系数（e=2.35）筛选离群光谱数据点，共筛选出马氏距离大于阈值的异常离群点38个（图5）。

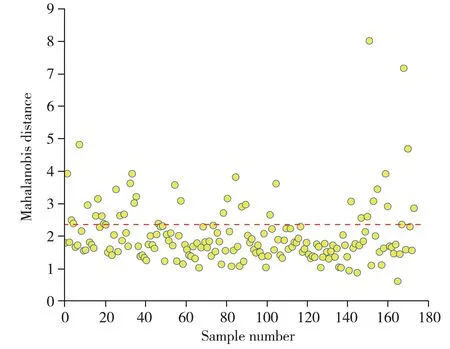
图5 基于多元散射校正光谱的训练集样本的马氏距离和最佳阈值Fig.5 Mahalanobis distance and optimal threshold of training set based on MSC spectra

对经多元散射校正、主成分分析及马氏距离异常值筛选的训练集光谱样本进行PLS建模，分析不同含水量砂岩样本特征值与含水量之间的相关关系。图6 分别为PLS 模型下训练集和测试集砂岩含水量与真实含水量的对比结果。

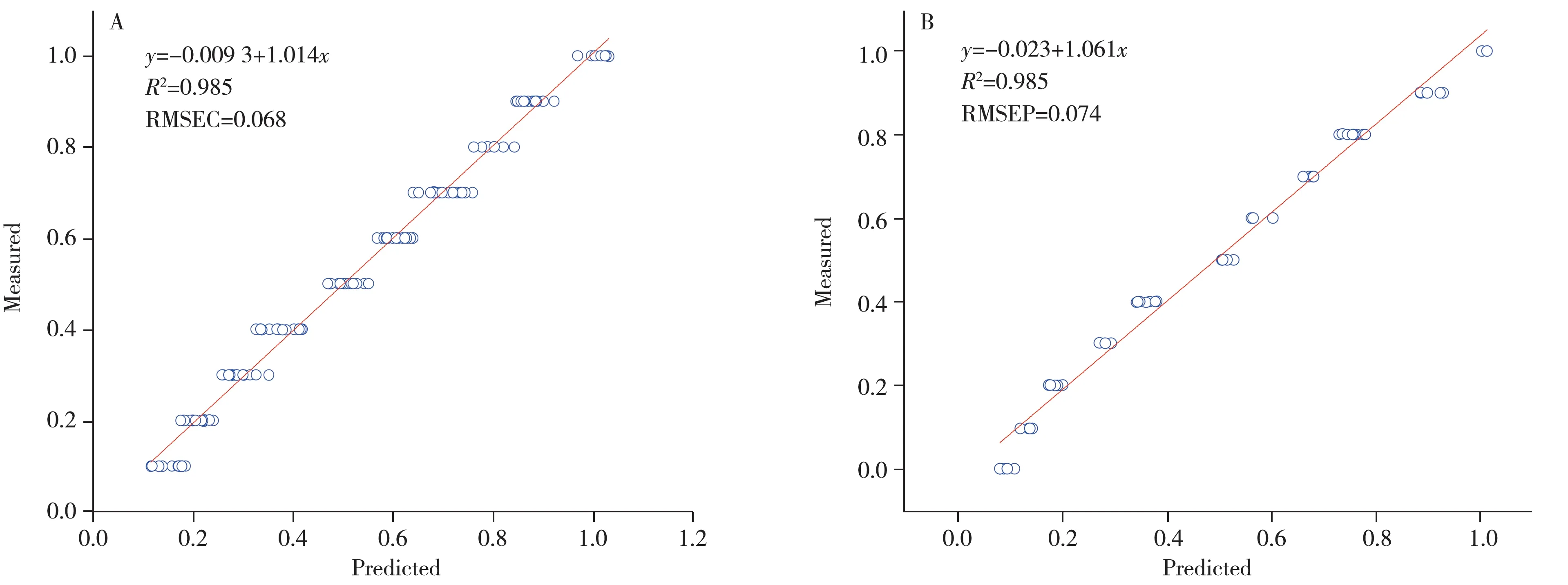
图6 PLS模型预测的含水量与真实含水量对比结果Fig.6 Comparison of water content between predicted by PLS model and measured

将真实含水量与预测含水量的相关系数（R2)、训练集的均方根误差（RMSEC）和测试集的均方根误差（RMSEP）作为模型评价指标。相关系数越高、均方根误差越低且主成分数越小，PLS模型的预测效果越好。

结果表明，基于多元散射校正、主成分分析与马氏距离构建的PLS 模型能够很好地预测砂岩含水量，训练集（173个样本）的R2为0.985，RMSEC为0.068；测试集（57个样本）的R2为0.985，RMSEP为0.074。此时的主成分数为11。

2.2.2 结合归一化特征向量提取与随机森林法的预测模型为更直观地获取不同含水量砂岩的有效信息，从光谱数据中选取R1和R2两个峰附近相对变化较为明显的波段标记为A1（7.023～7.612 μm）和A2（9.895～10.989 μm），以峰高H、半高宽FWHM、峰面积A、肩宽比S、基线的斜率K为特征变量。峰高H定义为：以横轴为零基线，经滤波和平滑校正后吸收峰所对应的光谱强度；半高宽FWHM 定义为：吸收谱带为最大高度一半时谱带的宽度；峰面积A定义为：以横坐标为基线所得的曲线积分面积；肩宽比S定义为：右肩宽（R）与左肩宽（L）长度之比。基线（连接吸收峰左右两肩的直线）斜率K按下式计算：

式中，λ1和λ2分别为左肩及右肩对应的波长，R1和R2分别为λ1和λ2对应的光谱吸光度。

上述5个特征变量构成了初始特征集N=｛H，FWHM，A，S，K｝。由于各个特征变量之间的量纲不同，导致提取相关性较强的特征变量变得困难，因此对原始特征变量进行归一化处理以快速筛选相关性较高的初始特征，避免因量纲不同导致的信息误差，归一化公式如下：

利用样本数据（xij）减去其相同列的最小值（min（xj）），再除以所在列的极差（max（xj）-min（xj）），即得到归一化后不同含水量砂岩的光谱（xij*）。A1波段和A2波段中红外光谱的初始特征变量数值分别如表2和表3所示，将全部230条中红外光谱曲线按照样品含水量不同进行标记，含水量为0 的测试样品的光谱数据记作0-1，0-2，0-3，...，含水量为10%的样品光谱数据记作1-1，1-2，1-3，...，以此类推。计算5 种特征变量与砂岩样品含水量之间的线性相关系数，如表4 所示。由表4 可知，A2波段中峰高H、半峰宽FWHM、峰面积A和肩宽比S，4个特征变量与含水量之间的相关性明显优于A1波段，由于该波段特征变量峰高H和峰面积A与含水量之间的相关系数均达到0.9 以上，其余特征变量与含水量的相关性较差，故将初始特征集N简化为F=｛H，A｝，即由峰高H和峰面积A两个特征变量构成特征集。

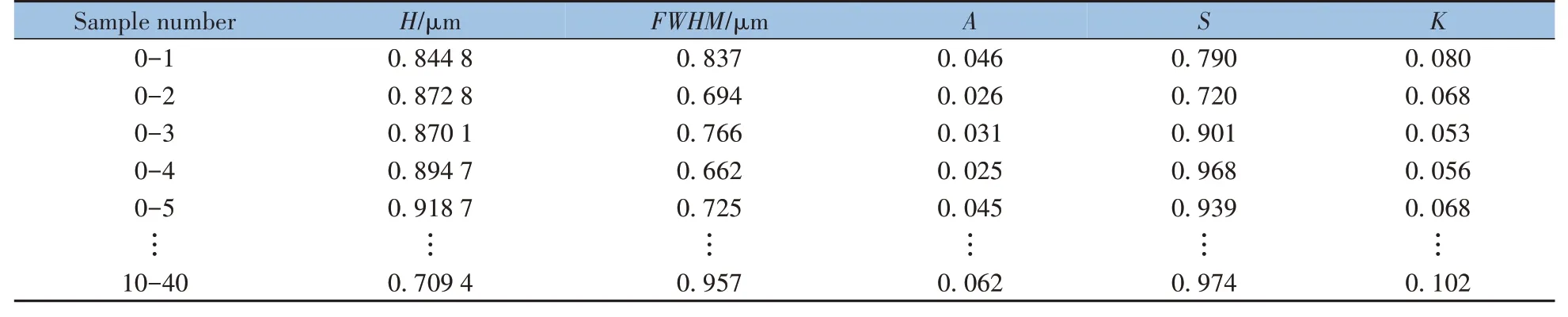
表2 A1波段归一化中红外光谱的初始特征变量Table 2 Initial characteristic variables of normalized MIR during A1 waveband

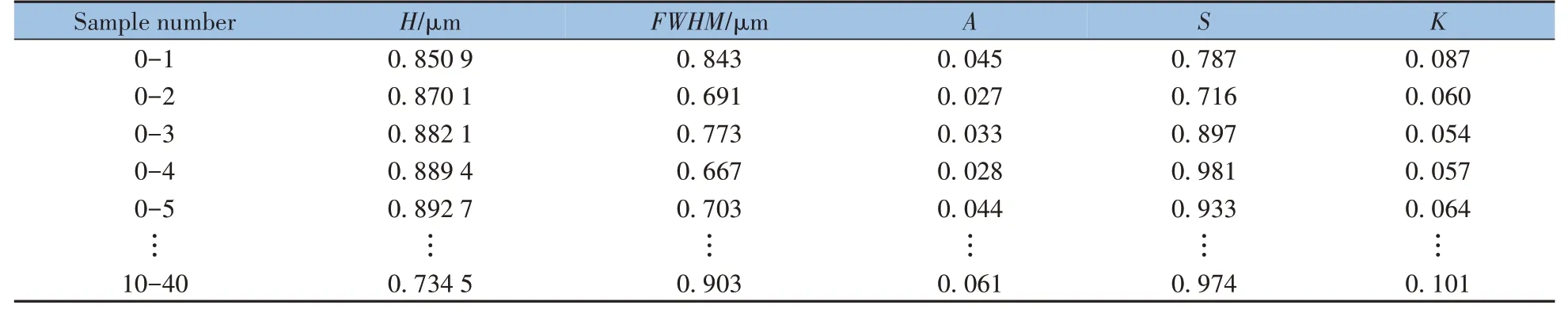
表3 A2波段归一化中红外光谱的初始特征变量Table 3 Initial characteristic variables of normalized MIR during A2 waveband

表4 两个敏感波段的特征变量与水分含量相关系数的绝对值Table 4 Two sensitive wavebands and absolute correlation coefficients between different spectral features and moisture contents

随机森林［15］具有可处理离散型、高维度无规则数据的优势，将上述两种特征变量结合随机森林进行建模。决策树的个数取100，特征变量为2。图7 为随机森林法得到的训练集与测试集砂岩预测含水量与真实含水量的对比结果。可以看出，训练集和测试集的预测含水量与真实含水量的R2均为0.995，RMSEC和RMSEP分别为0.021、0.022，说明该模型预测能力较好。

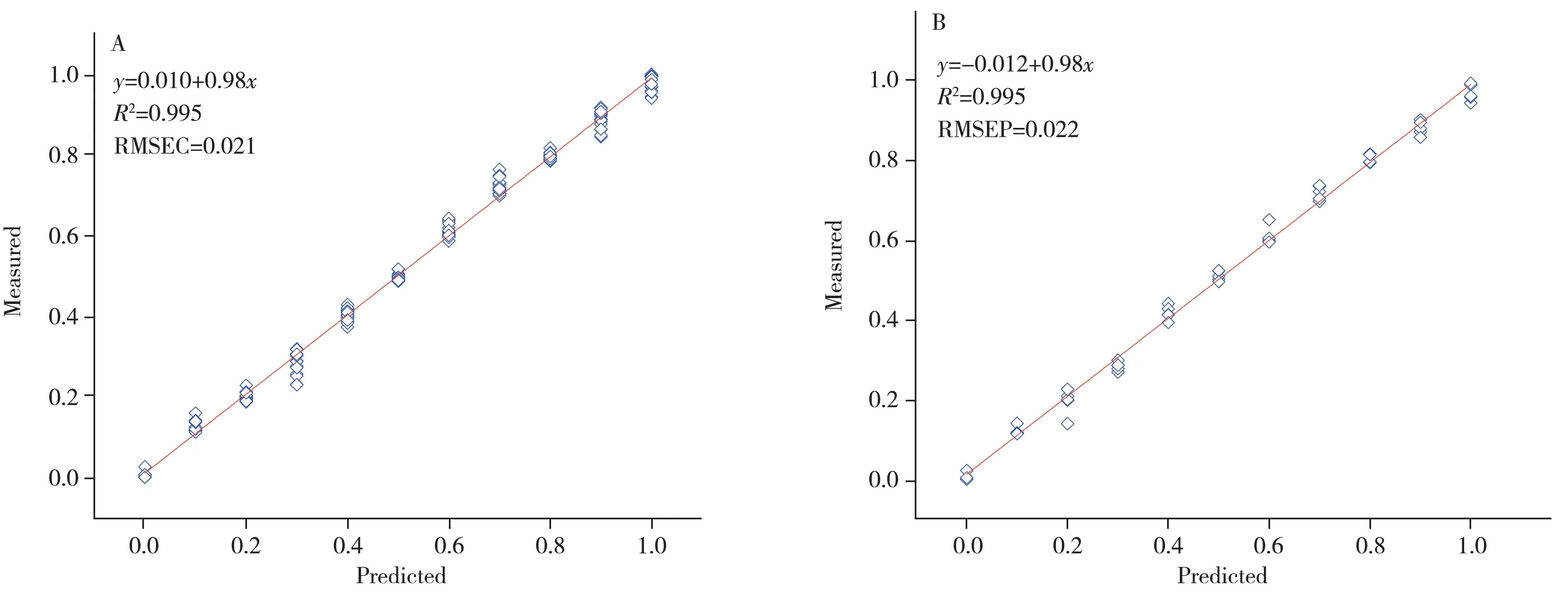
图7 随机森林法预测的含水量与真实含水量对比结果Fig.7 Comparison of water content between predicted by random forest method and measured

2.2.3 基于一阶微分法的支持向量机预测模型微分处理［16］是光谱基线校正的方法之一，可以去除背景噪声或漂移对光谱信号产生的影响，其中一阶微分法可有效消除曲线背景噪声，提高光谱分辨率。基本公式如下：

式中，x'n为一阶微分处理后的光谱数据，xn为第n个样品的光谱，xn+g为第n个样品经过g窗口宽度变换的光谱数据，g为窗口宽度。

对一阶微分变换后的光谱数据进行支持向量机（SVM）分类，确保学习过程中得到的极值解为最优解。利用高斯核函数（RBF kernel）选择最优相关参数，SVM模型的核参数γ为RBF函数自带的参数，惩罚系数C为1.0。基于一阶微分变换采用SVM 算法［17］进行定量分析，结果如图8 所示。数据集中包括173 个训练集和57 个测试集样本，训练集预测的含水量与真实含水量的R2为0.997，RMSEC 为0.034，测试集的R2为0.951，RMSEP为0.137。训练集与测试集的均方根误差相差较大，说明模型的预测能力一般。

图8 基于SVM的预测含水量与真实含水量对比结果Fig.8 Comparison of water content between predicted by SVM and measured

由上述3 种建模结果可知，不同预处理方法下的建模效果不同。可以看出，结合SG 平滑的3 种处理方法中，由于特征变量筛选可对原始光谱数据进行降维，得到强相关性的参数（峰高和峰面积），避免了全波段多特征的复杂原始数据难以准确分辨特征变量的问题，得到了最佳的建模效果，即基于归一化特征变量提取结合随机森林的建模效果最佳。

3 结 论

本文通过分析砂岩的中红外光谱随样品含水量的变化，选取与含水量高度相关、位于7.23 μm 和10.41 μm附近的两个特征峰的峰高和峰面积作为特征变量，采用随机森林法建立了砂岩含水量的预测模型，获得了比基于MSC 光谱建立的PLS模型及基于一阶微分光谱建立的SVM 模型更为精准的预测结果，为基于红外光谱技术实现砂岩含水量的无损、快速分析提供了解决方案。